저항 센서 브리지를 선형화하는 두 가지 기술

저항 센서의 미세한 저항 변화를 측정하는 것은 어려운 작업일 수 있습니다. 다음은 브리지 비선형성 오류를 제거하는 두 가지 하드웨어 방법입니다.

저항성 센서의 저항은 온도나 힘과 같은 물리적 변수에 따라 달라집니다. 이러한 장치의 저항 변화율은 일반적으로 작습니다. 예를 들어, 스트레인 게이지 저항의 총 변화는 전체 작동 범위에서 1% 미만일 수 있습니다.

이러한 작은 값을 식별하려면 매우 정확한 측정 회로가 필요합니다. 브리지 회로를 사용하면 이러한 정확한 측정을 보다 쉽게 ​​수행할 수 있습니다. 그러나 브리지 회로의 출력은 선형 센서를 사용하더라도 측정된 물리적 변수와 비선형 관계를 가질 수 있습니다.

이러한 경우 소프트웨어 또는 하드웨어 기술을 사용하여 브리지 비선형성 오류를 제거할 수 있습니다. 이 기사에서는 저항성 센서 브리지를 선형화하는 두 가지 기술을 살펴보겠습니다.

저항 센서의 브리지 비선형성

다음과 같은 선형 응답을 갖는 저항성 압력 센서를 고려하십시오.

\[R_{센서} =R_0 + Mx\]

여기서 R₀ 는 제로 압력에서 센서의 초기 저항, x는 측정량(압력)의 값, M은 센서 응답의 기울기입니다. 미래 방정식을 더 간단하게 만들기 위해 M 값이 센서의 초기 저항 값(R₀ ) 따라서 센서 응답은 \[R_0(1+x)\]입니다.

일반적으로 저항성 센서의 저항 변화율은 작기 때문에 정확한 측정을 보다 쉽게 ​​수행하려면 브리지 회로를 사용해야 합니다. 이 센서의 일반적인 브리지 구성은 그림 1에 나와 있습니다.

그림 1. 저항성 센서의 일반적인 브리지 구성

브리지의 다른 3개의 저항은 저항이 R₀입니다. . 이 브리지 저항을 선택하면 출력의 감도(V_out ) 센서 저항의 변화. 출력 방정식은 다음과 같이 얻을 수 있습니다.

\[V_{out} =V_A - V_B =V_r\left(\frac{R_0(1+x)}{R_0+R_0(1+x)} - \frac {1}{2}\오른쪽)\]

이렇게 하면 다음이 간소화됩니다.

\[V_{out} =V_r\left(\frac{x}{2(2+x)}\right)\]

방정식 1.

보시다시피 브리지 출력과 저항값(x)의 변화 사이의 관계는 선형이 아닙니다. \[x\ll2\]를 사용하여 위의 방정식을 다음과 같은 선형 관계로 근사할 수 있습니다.

\[V_{out} \approx V_r\left(\frac{x}{4}\right)\]

방정식 2.

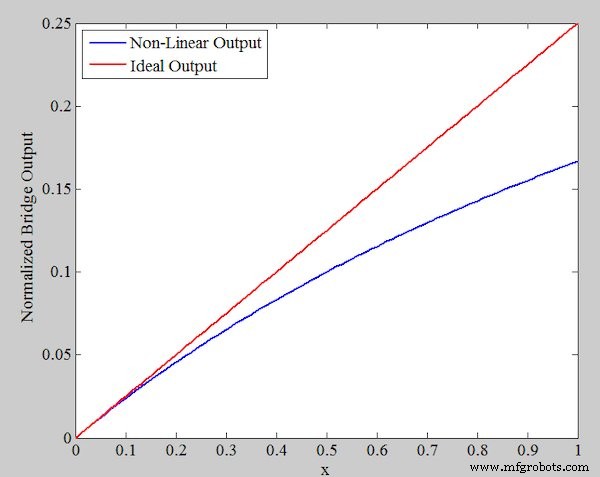
그림 2는 브리지 \[\frac{V_{out}}{V_r}\] 의 정규화된 출력을 보여줍니다. 실제 경우(방정식 1)와 이상적인 출력(방정식 2) 모두에 대해.

그림 2. 방정식 1 및 2의 비선형(파란색) 및 이상적인(빨간색) 출력

예상대로 선형 응답으로부터의 편차는 x에 따라 증가합니다.

얼마나 많은 비선형성 오류가 도입될까요?

위의 브리지 회로의 비선형성 오류를 정량화해 보겠습니다. 식 1을 다음과 같이 다시 쓸 수 있습니다.

\[V_{out} =V_r \left(\frac{x}{4}\right) \left(\frac{1}{1+ \frac{x} {2}}\오른쪽)\]

가정 \[\frac{x}{2} <<1\], 우리는 Taylor의 정리를 사용하여 위 함수의 근사치를 다음과 같이 얻을 수 있습니다.

\[V_{out} =V_r\left(\frac{x}{4}\right)\left(1 - \frac{x}{2}\right) \]

이 결과를 방정식 2와 비교하여 오류의 크기를 다음과 같이 계산할 수 있습니다.

\[E_{비선형성} =V_r\left(\frac{x}{4}\right)\left(\frac{x}{2}\right) \]

이것을 방정식 2에 의해 주어진 예상되는 이상적인 값으로 나누면 주어진 저항(x)의 변화에 ​​대한 백분율 종점 선형성 오류를 얻을 수 있습니다.

\[백분율~오류 =\frac{x}{2} \times 100\%\]

비선형 오차 계산의 예

응답이 \[R_{sensor} =R_0(1+x)\]인 센서를 고려하십시오. \[R_0 =100~\Omega\]이고 전체 작동 범위에서 x의 최대값은 0.01이라고 가정합니다. 최대 선형성 오류 백분율은 다음과 같습니다.

\[백분율~오류 =\left(\frac{0.01}{2}\right) \times 100\% =0.5\%\]

소프트웨어를 사용하여 센서 선형성 오류를 제거할 수는 있지만 선형 응답을 갖는 것이 측정 정밀도를 높이고 시스템 보정을 용이하게 하기 때문에 바람직합니다. 브리지 회로를 선형화하는 데 사용할 수 있는 다양한 회로 토폴로지가 있습니다.

이 기사의 나머지 부분에서는 두 가지 브리지 선형화 기술을 살펴보겠습니다.

방법 1:저항 변화(x)에 비례하는 전압 생성

이 기사에서 논의할 첫 번째 선형화 기술은 그림 3에 나와 있습니다. 먼저 이 기술의 기본 아이디어를 검토한 다음 그림 3의 회로가 이 아이디어를 구현하는 방법을 살펴보겠습니다.

그림 3. 저항성 센서 브리지를 선형화하기 위한 회로 유형

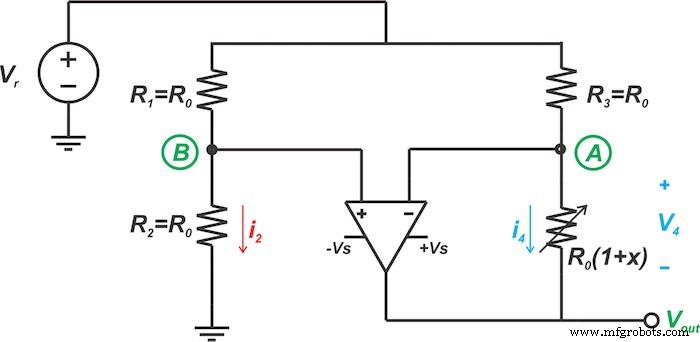
그림 4는 \[I_{Ref}\] 의 고정 전류를 나타냅니다. 선형 센서를 통해 강제로 흐릅니다.

그림 4. 고정 전류(I_Ref ) 선형 센서를 통해 강제됨

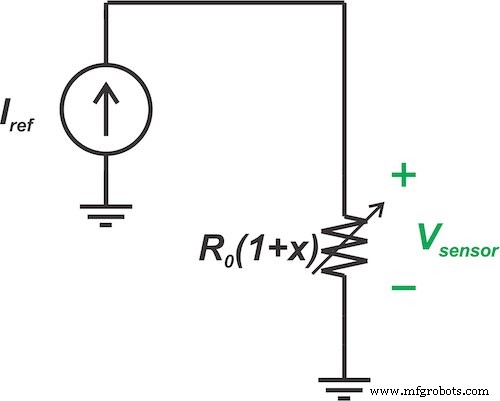
이 시나리오에서 센서 양단의 결과 전압은 다음과 같습니다.

\[V_{센서} =I_{Ref} \times R_0(1 + x)\]

다음과 같이 재정렬할 수 있습니다.

\[V_{센서} =R_0 \times I_{Ref} + R_0 \times I_{Ref} \times x\]

첫 번째 항은 일정한 값이고 두 번째 항은 센서 저항(x)의 변화에 ​​비례합니다. 상수 항을 생략할 수 있다면 x와 선형 관계를 갖는 전압을 갖게 됩니다.

회로 구현

그림 3의 회로는 위의 아이디어를 사용하여 브리지 회로를 선형화합니다. 연산 증폭기 입력은 이상적으로 전류를 소비하지 않으므로 노드 B의 전압은 다음과 같은 일정한 값을 갖습니다.

\[v_B =\frac{R_0}{R_0 + R_0}V_r =\frac{V_r}{2}\]

연산 증폭기의 높은 이득과 함께 네거티브 피드백은 연산 증폭기의 반전 및 비반전 입력이 모두 동일한 전압을 갖도록 합니다.

\[v_A =v_B =\frac{V_r}{2}\]

R3의 양 끝은 일정한 전위에 있으므로 이를 통해 일정한 전류가 흐릅니다. 즉, 연산 증폭기는 R3이 \[\frac{V_r}{2R_0}\]의 정전류를 센서로 강제하는 전류 소스로 작동하게 합니다. 따라서 센서 양단의 전압은 다음과 같습니다.

\[V_4 =\frac{V_r}{2R_0} \times R_0(1 + x) =\frac{V_r}{2} + \frac{V_r}{2} x\]

첫 번째 항은 V_out에서 제거되어야 하는 상수 값입니다. 방정식. 두 번째 항은 센서 저항 변화(x)에 비례하며 출력 방정식에 나타나야 합니다. Kirchhoff의 전압 법칙을 적용하면 V_out를 찾습니다. 다음과 같이:

\[V_{out} =-V_4 + V_A =- \left(\frac{V_r}{2} + \frac{V_r}{2}x\right) + V_A\]

따라서 V_A만 필요합니다. \[\frac{V_r}{2}\]와 같아야 합니다. 이는 이미 충족되어 다음과 같은 결과를 가져옵니다.

\[V_{out} =-\frac{V_r}{2}x\]

따라서 출력은 x와 선형 관계를 갖습니다.

방법 2:저항 변화(x)에 비례하는 전류 생성

이 기사에서 논의할 두 번째 브리지 선형화 기술은 그림 5에 나와 있습니다.

그림 5. 저항성 센서 브리지의 아날로그 선형화를 위한 또 다른 회로

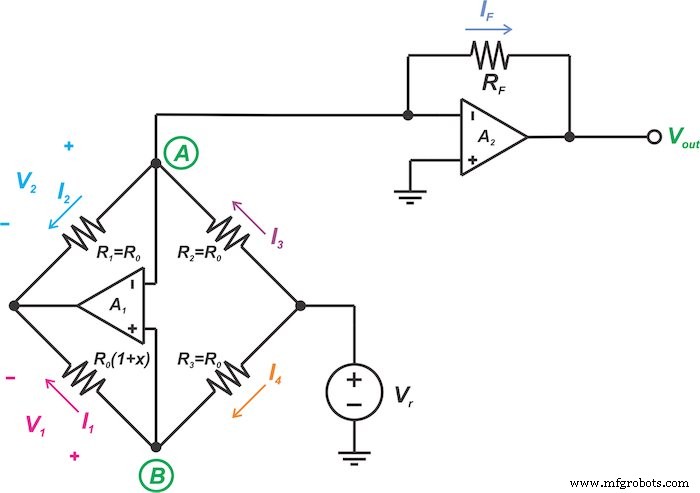
이 기술의 기본 아이디어를 다시 살펴보고 회로 구현을 살펴보겠습니다.

이 두 번째 선형화 기술은 그림 6에 나와 있습니다.

그림 6. 센서의 저항에 비례하도록 회로의 분기를 통과하는 전류를 강제하는 선형화 기술

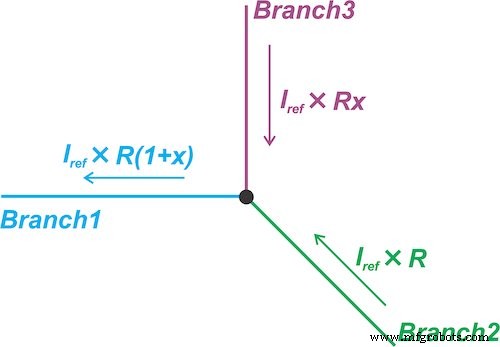
이것은 센서 저항에 비례하도록 회로의 분기(분기 1)를 통한 전류를 강제합니다.

\[I_1 =I_{Ref} \times R_0(1 + x)\]

여기서 나는_참조 상수 값입니다. 그런 다음 현재 영역 빼기를 수행하여 상수 항 \[I_{Ref} \times R_0\]을 제거합니다. 이를 위해 Branch 2에 흐르는 전류는 \[I_{Ref} \times R_0\]로 설정됩니다. 따라서 분기 3을 통한 전류는 \[I_{Ref} \times R_0x\]—가 됩니다. 센서 저항(x)의 변화에 ​​비례합니다.

회로 구현

그림 5의 회로가 위의 아이디어를 어떻게 구현하는지 봅시다. 다시 말하지만, 연산 증폭기의 높은 이득과 함께 네거티브 피드백은 두 연산 증폭기의 반전 및 비반전 입력을 모두 강제합니다(둘 모두 A₁ 그리고 A₂ ) 동일한 전압:

\[v_A =v_B =0\]

방정식 3.

따라서 V₁ =V₂ 로 이어지는

\[R_0 (1 + x) \times I_1 =R_0 \times I_2\]

이렇게 하면 다음이 간소화됩니다.

\[I_2 =I_1 + I_1 \times x\]

방정식 4.

나는₁ =나₄ 방정식 3을 고려하면 다음과 같습니다.

\[I_1 =I_4 =\frac{V_r - v_A}{R_0} =\frac{V_r}{R_0}\]

이를 식 4에 대입하면 다음을 얻습니다.

\[I_2 =\frac{V_r}{R_0} + \frac{V_r}{R_0} \times x\]

따라서 나는₂ 상수 값과 x에 비례하는 항의 합입니다. 출력 전류 방정식에서 상수 항을 제거하기 위해 Kirchhoff의 전류 법칙만 사용하면 됩니다. R2를 통한 전류는 \[\frac{V_r}{R_0}\] 와 같은 전류를 공급합니다. 노드 A로 연결:

\[I_F =-\frac{V_r}{R_0} \times x\]

따라서 다음을 얻습니다.

\[V_{out} =V_r \times \frac{R_F}{R_0} \times x\]

그림 5의 회로는 첫 번째 기술에 비해 추가 연산 증폭기가 필요합니다. 그러나 두 개의 연산 증폭기 솔루션을 사용하면 \[\frac{R_F}{R_0}\] 비율을 선택하여 이득을 임의로 설정할 수 있습니다.

<시간 />

내 기사의 전체 목록을 보려면 이 페이지를 방문하십시오.