산업기술








혼합 주파수 신호에 대한 장에서 우리는 고조파의 개념을 탐구했습니다. AC 시스템:기본 소스 주파수의 정수 배수인 주파수.
AC 발전기(교류기)에서 나오는 소스 전압 파형이 왜곡되지 않은 단일 주파수 사인파로 가정되는 AC 전원 시스템의 경우 고조파 성분이 없어야 합니다. . . 이상적으로.
비선형 구성요소가 아니라면 사실일 것입니다. . 비선형 구성 요소는 소스 전압에 대해 불균형적으로 전류를 끌어서 비사인파 전류 파형을 유발합니다.
비선형 구성 요소의 예로는 가스 방전 램프, 반도체 전력 제어 장치(다이오드, 트랜지스터, SCR, TRIAC), 변압기(1차 권선 자화 전류는 일반적으로 코어의 B/H 포화 곡선으로 인해 비정현파) 및 전기 모터(다시 말하지만, 모터 코어 내의 자기장이 포화 수준 근처에서 작동할 때).
백열등도 온도의 급격한 변동으로 인해 사이클 전체에 걸쳐 필라멘트 저항이 변하기 때문에 약간의 비정현파 전류를 생성합니다.
혼합 주파수 장에서 배웠듯이 모든 다른 사인파 모양의 파형의 왜곡은 고조파 주파수의 존재를 구성합니다.
문제의 비사인파 파형이 평균 중심선 위와 아래에서 대칭인 경우 고조파 주파수는 짝수 정수 배수 없이 기본 소스 주파수의 홀수 정수 배수만 됩니다.
대부분의 비선형 부하는 이와 같은 전류 파형을 생성하므로 짝수 번째 고조파(2차, 4차, 6차, 8차, 10차, 12차 등)는 대부분의 AC 전원 시스템에 없거나 최소한으로만 존재합니다.
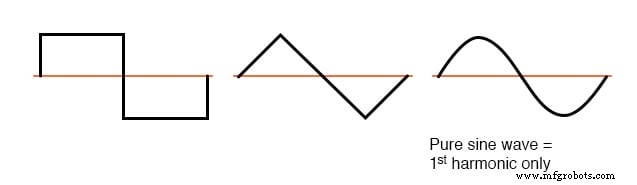
대칭 파형의 예 - 홀수 고조파만 해당
짝수 고조파가 존재하는 비대칭 파형의 예는 아래 그림에서 참조용으로 표시됩니다.
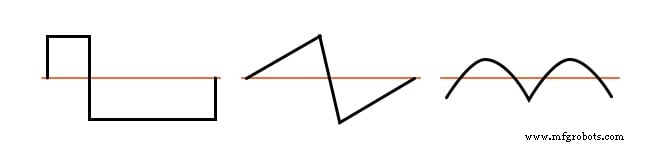
비대칭 파형의 예(고조파도 존재)
가능한 고조파 주파수의 절반이 일반적으로 비선형 부하의 대칭 왜곡에 의해 제거되지만 홀수 고조파는 여전히 문제를 일으킬 수 있습니다. 이러한 문제 중 일부는 단상이든 아니든 모든 전력 시스템에 일반적입니다.
예를 들어, 와전류 손실로 인한 변압기 과열은 모든에서 발생할 수 있습니다. 상당한 고조파 성분이 있는 AC 전원 시스템.
그러나 다상 전력 시스템에 고유한 고조파 전류에 의해 발생하는 몇 가지 문제가 있으며 이 섹션에서는 이러한 문제에 대해 특별히 설명합니다.
SPICE에서 비선형 부하를 시뮬레이션할 수 있어 복잡한 수학을 많이 피하고 조화 효과에 대한 보다 직관적인 이해를 얻는 데 도움이 됩니다.
먼저, 순전히 선형 부하와 모든 관련 저항이 있는 단일 사인파 전압 소스인 매우 간단한 AC 회로로 시뮬레이션을 시작합니다.
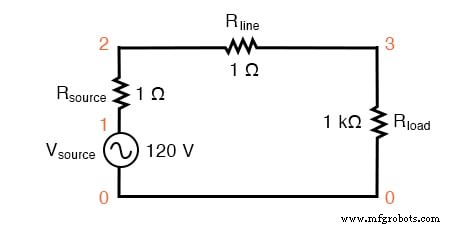
단일 사인파 소스가 있는 SPICE 회로.
R소스 및 R줄 이 회로의 저항은 실제 세계를 모방하는 것 이상을 수행합니다. SPICE 시뮬레이션에서 전류를 측정하기 위한 편리한 션트 저항도 제공합니다. .
R라인에서 측정된 전압에 대한 푸리에 분석을 사용한 이 회로의 SPICE 시뮬레이션(SPICE 목록:"선형 부하 시뮬레이션") 이 회로의 라인 전류의 고조파 내용을 보여주어야 합니다. 본질적으로 완전히 선형이기 때문에 60Hz 소스를 가정할 때 60Hz의 1차(기본) 이외의 고조파가 예상되지 않아야 합니다.
SPICE 출력 "과도 응답 v(2,3)의 푸리에 구성 요소" 및 아래 그림을 참조하십시오.
<사전>선형 하중 시뮬레이션 vsource 1 0 sin(0 120 60 0 0) 리소스 1 2 1 라인 2 3 1 로드 3 0 1k .옵션 itl5=0 .트란 0.5m 30m 0 1u .plot tran v(2,3) .4 60 v(2,3) .끝 <사전> 과도 응답 v(2,3)의 푸리에 성분 DC 구성 요소 =4.028E-12 고조파 주파수 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 5.793E-12 0.000000 51.122 123.122 3 1.800E+02 7.407E-12 0.000000 -34.624 37.376 4 2.400E+02 9.056E-12 0.000000 4.267 76.267 5 3.000E+02 1.651E-11 0.000000 -83.461 -11.461 6 3.600E+02 3.931E-11 0.000000 36.399 108.399 7 4.200E+02 2.338E-11 0.000000 -41.343 30.657 8 4.800E+02 4.716E-11 0.000000 53.324 125.324 9 5.400E+02 3.453E-11 0.000000 21.691 93.691 총 고조파 왜곡 =0.000000퍼센트
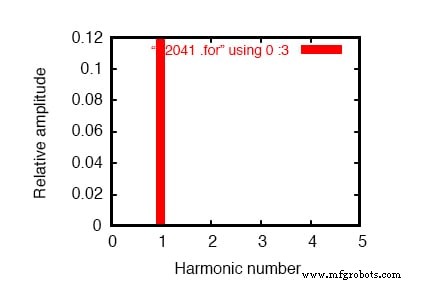
단일 주파수 성분의 주파수 영역 플롯. SPICE 목록:"선형 부하 시뮬레이션"을 참조하십시오.
.plot 명령은 SPICE 넷리스트에 나타나며 일반적으로 사인파 그래프 출력이 됩니다. 그러나 이 경우에는 간결함을 위해 의도적으로 파형 표시를 생략했습니다. .plot 명령은 단순히 SPICE의 푸리에 변환 기능의 단점을 만족시키기 위해 넷리스트에 있습니다.
이산 푸리에 변환은 완벽하지 않으므로 SPICE가 푸리에 분석을 수행하는 한 최대 9차 고조파(표)까지의 모든 주파수에 대해 표시된 매우 작은 고조파 전류(피코 증폭기 범위에서!)를 볼 수 있습니다. .
1차 고조파의 "푸리에 성분" 또는 예상 부하 전류인 기본 주파수에 대해 0.1198A(1.198E-01)를 표시합니다. 소스 전압이 120V이고 부하 저항이 1인 경우 약 120mA입니다. kΩ.
다음으로 고조파 전류를 생성하기 위해 비선형 부하를 시뮬레이션하고 싶습니다. 이것은 근본적으로 다른 두 가지 방법으로 수행할 수 있습니다. 한 가지 방법은 SPICE로 시뮬레이션하기 쉬운 다이오드 또는 기타 반도체 장치와 같은 비선형 구성 요소를 사용하여 부하를 설계하는 것입니다. 다른 하나는 부하 저항과 병렬로 일부 AC 전류 소스를 추가하는 것입니다.
후자의 방법은 알려진 값의 현재 소스가 매우 복잡한 응답 특성을 가진 구성 요소보다 수학적 네트워크 분석에 더 적합하기 때문에 엔지니어가 고조파 시뮬레이션을 위해 선호하는 경우가 많습니다.
SPICE가 모든 수학 작업을 수행하도록 하기 때문에 반도체 구성 요소의 복잡성은 우리에게 문제를 일으키지 않지만 전류 소스는 임의의 양의 전류(편리한 기능)를 생성하도록 미세 조정될 수 있으므로 아래 그림과 SPICE 목록 "비선형 부하 시뮬레이션"에 표시된 후자의 접근 방식을 선택합니다.
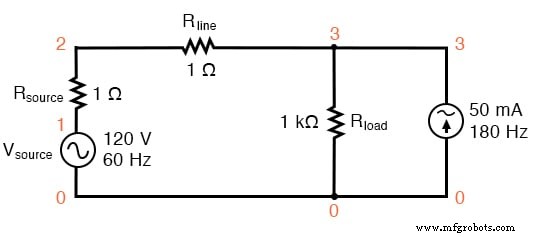
SPICE 회로:3차 고조파가 추가된 60Hz 소스
<사전> 비선형 부하 시뮬레이션 vsource 1 0 sin(0 120 60 0 0) 리소스 1 2 1 라인 2 3 1 로드 3 0 1k i3har 3 0 sin(0 50m 180 0 0) .옵션 itl5=0 .트란 0.5m 30m 0 1u .plot tran v(2,3) .4 60 v(2,3) .끝
이 회로에는 50mA 크기의 전류 소스와 60Hz 소스 주파수의 3배인 180Hz의 주파수가 있습니다. 1kΩ 부하 저항과 병렬로 연결하면 전류가 저항과 함께 추가되어 비사인파 전체 라인 전류가 됩니다.
이 3차 고조파 전류가 일반적으로 일반 사인파인 전체 전류에 미치는 영향을 볼 수 있도록 아래 그림에 파형 플롯을 표시하겠습니다.
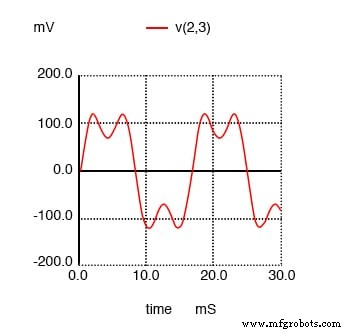
60Hz 소스와 180Hz의 3차 고조파의 합계를 보여주는 SPICE 시간 영역 플롯
과도 응답 v(2,3)의 푸리에 성분 DC 성분 =1.349E-11 고조파 주파수 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 1.609E-11 0.000000 67.570 139.570 3 1.800E+02 4.990E-02 0.416667 144.000 216.000 4 2.400E+02 1.074E-10 0.000000 -169.546 -97.546 5 3.000E+02 3.871E-11 0.000000 169.582 241.582 6 3.600E+02 5.736E-11 0.000000 140.845 212.845 7 4.200E+02 8.407E-11 0.000000 177.071 249.071 8 4.800E+02 1.329E-10 0.000000 156.772 228.772 9 5.400E+02 2.619E-10 0.000000 160.498 232.498 총 고조파 왜곡 =41.666663%
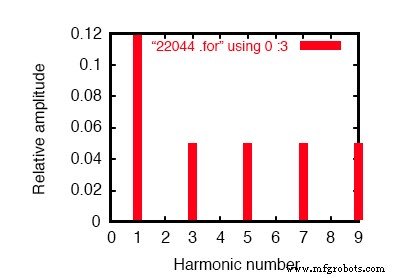
60Hz 소스와 180Hz의 3차 고조파를 보여주는 SPICE 푸리에 플롯
푸리에 분석에서(위 그림 및 "과도 응답 v(2,3)의 푸리에 구성 요소" 참조) 혼합 주파수는 혼합되지 않고 별도로 표시됩니다.
여기에서 첫 번째 시뮬레이션에서와 동일한 60Hz(기본) 전류 0.1198A를 볼 수 있지만 3차 고조파 행에 나타나는 49.9mA:작동 중인 50mA, 180Hz 전류 소스입니다. 라인을 통해 전체 50mA가 표시되지 않는 이유는 무엇입니까?
해당 전류 소스는 1kΩ 부하 저항을 통해 연결되므로 일부 전류는 부하를 통해 분류되고 라인을 통해 소스로 다시 가지 않습니다. 부하의 한 부분은 "정상"(저항기)이고 다른 부분은 전류 소스에 의해 모방되는 이러한 유형의 시뮬레이션의 불가피한 결과입니다.
"부하"에 더 많은 전류 소스를 추가하면 이상적인 사인파 모양에서 라인 전류 파형의 추가 왜곡이 표시되고 이러한 각 고조파 전류는 푸리에 분석 분석에 나타납니다. 아래 그림과 SPICE 목록:"비선형 부하 시뮬레이션"을 참조하십시오.
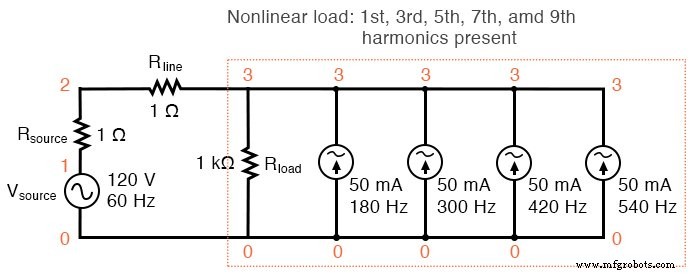
비선형 부하:1차, 3차, 5차, 7차 및 9차 고조파가 있습니다.
비선형 하중 시뮬레이션 vsource 1 0 sin(0 120 60 0 0) 리소스 1 2 1 라인 2 3 1 로드 3 0 1k i3har 3 0 sin(0 50m 180 0 0) i5har 3 0 sin(0 50m 300 0 0) i7har 3 0 sin(0 50m 420 0 0) i9har 3 0 sin(0 50m 540 0 0) .옵션 itl5=0 .트란 0.5m 30m 0 1u .plot tran v(2,3) .four 60 v(2,3) .end
과도 응답 v(2,3)의 푸리에 성분 DC 성분 =6.299E-11 고조파 주파수 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E+02 4.990E-02 0.416667 144.000 216.000 4 2.400E+02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E+02 4.990E-02 0.416667 0.000 72.000 6 3.600E+02 6.271E-09 0.000000 85.062 157.062 7 4.200E+02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E+02 2.742E-09 0.000000 -38.781 33.219 9 5.400E+02 4.990E-02 0.416666 72.000 144.000 총 고조파 왜곡 =83.333296%

푸리에 분석:"과도 응답 v(2,3)의 푸리에 구성요소".
푸리에 분석(위 그림)에서 볼 수 있듯이 모든 고조파 전류 소스는 각각 49.9mA에서 라인 전류에 동일하게 표시됩니다. 지금까지는 단상 전력 시스템 시뮬레이션일 뿐입니다.
3단계 시뮬레이션으로 만들면 상황이 더욱 흥미로워집니다. 두 개의 푸리에 분석이 수행됩니다. 하나는 라인 저항 양단의 전압에 대한 것이고 다른 하나는 중성 저항 양단의 전압에 대한 것입니다.
이전과 마찬가지로 각각 1Ω의 고정 저항에 걸친 전압을 읽으면 해당 저항을 통과하는 전류를 직접적으로 알 수 있습니다. 아래 그림과 "고조파가 있는 Y-Y 소스/부하 4선식 시스템"을 나열하는 SPICE를 참조하십시오.
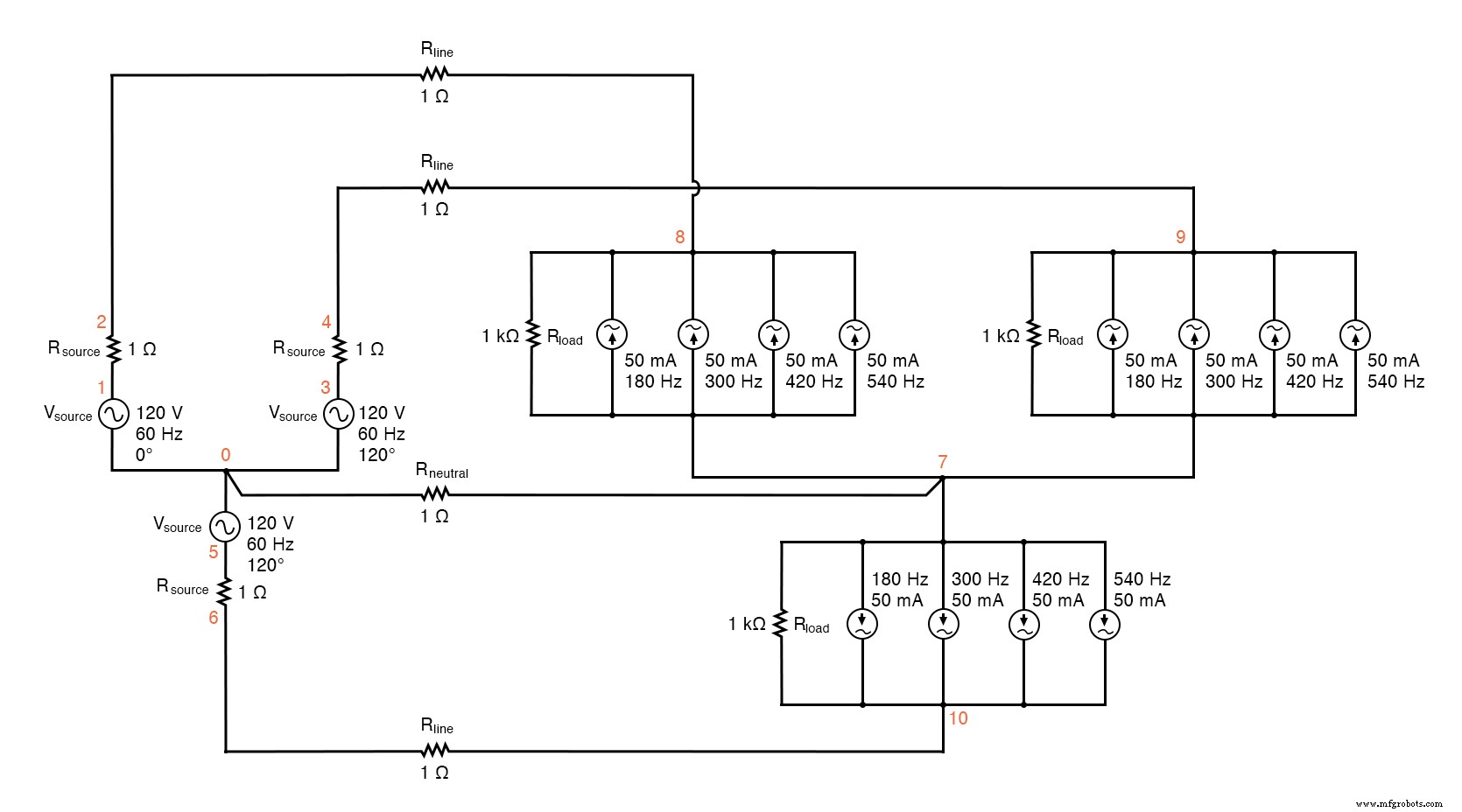
SPICE 회로:"라인 전류" 및 "중성 전류" 분석, 고조파가 있는 Y-Y 소스/부하 4선식 시스템
고조파가 있는 Y-Y 소스/부하 4선식 시스템 * * Phase1 전압 소스 및 r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) 리소스1 1 2 1 * * phase2 전압 소스 및 r(120 v /_ 120 deg) vsource2 3 0 sin(0 120 60 5.55555m 0) 리소스2 3 4 1 * * phase3 전압 소스 및 r(120 v /_ 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) 리소스3 5 6 1 * * 라인 및 중성선 저항 rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 중립 0 7 1 * * 부하의 1단계 rload1 8 7 1k i3har1 8 7 죄(0 50m 180 0 0) i5har1 8 7 죄(0 50m 300 0 0) i7har1 8 7 죄(0 50m 420 0 0) i9har1 8 7 죄(0 50m 540 0 0) * * 부하의 2단계 rload2 9 7 1k i3har2 9 7 sin(0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin(0 50m 420 5.55555m 0) i9har2 9 7 sin(0 50m 540 5.55555m 0) * * 부하의 3단계 rload3 10 7 1k i3har3 10 7 sin(0 50m 180 11.1111m 0) i5har3 10 7 sin(0 50m 300 11.1111m 0) i7har3 10 7 sin(0 50m 420 11.1111m 0) i9har3 10 7 sin(0 50m 540 11.1111m 0) * * 분석 물건 .옵션 itl5=0 .트란 0.5m 100m 12m 1u .plot tran v(2,8) .4 60 v(2,8) .plot tran v(0,7) .4 60 v(0,7) .끝
과도 응답 v(2,8)의 푸리에 성분 DC 구성 요소 =-6.404E-12 고조파 주파수 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.218E-10 0.000000 172.985 172.985 3 1.800E+02 4.975E-02 0.415423 0.000 0.000 4 2.400E+02 4.236E-10 0.000000 166.990 166.990 5 3.000E+02 4.990E-02 0.416667 0.000 0.000 6 3.600E+02 1.877E-10 0.000000 -147.146 -147.146 7 4.200E+02 4.990E-02 0.416666 0.000 0.000 8 4.800E+02 2.784E-10 0.000000 -148.811 -148.811 9 5.400E+02 4.975E-02 0.415422 0.000 0.000 총 고조파 왜곡 =83.209009%
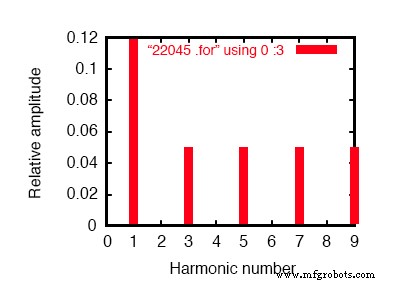
밸런스드 Y-Y 시스템에서 라인 전류의 푸리에 분석
과도 응답 v(0,7)의 푸리에 성분 DC 성분 =1.819E-10 고조파 주파수 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 6.000E+01 4.337E-07 1.000000 60.018 0.000 2 1.200E+02 1.869E-10 0.000431 91.206 31.188 3 1.800E+02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E+02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E+02 9.023E-07 2.080596 119.981 59.963 6 3.600E+02 3.396E-10 0.000783 15.882 -44.136 7 4.200E+02 1.264E-06 2.913955 59.993 -0.025 8 4.800E+02 5.975E-10 0.001378 35.584 -24.434 9 5.400E+02 1.493E-01 344147.4889 -179.999 -240.017
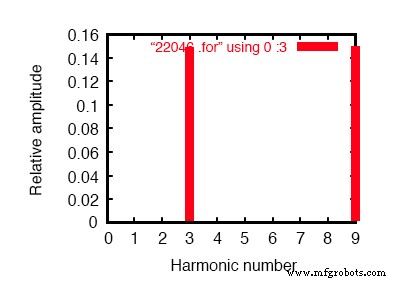
중성 전류의 푸리에 분석은 고조파가 없는 경우를 제외하고 표시합니다! 위 그림의 라인 전류와 비교하십시오.
이것은 균형 잡힌 Y-Y 전원 시스템이며 각 위상은 이전에 시뮬레이션된 단상 AC 시스템과 동일합니다. 결과적으로 3상 시스템의 한 위상에서 라인 전류에 대한 푸리에 분석이 단상 시스템의 라인 전류에 대한 푸리에 분석과 거의 동일하다는 것은 놀라운 일이 아닙니다. 각각 약 50mA의 0.1198A 및 홀수 고조파 전류.
위의 그림과 푸리에 분석을 참조하십시오. "과도 응답 v(2,8)의 푸리에 구성요소"
여기서 놀라운 것은 Rneutral 양단의 전압 강하에 의해 결정되는 중성선의 전류에 대한 분석입니다. SPICE 노드 0과 7 사이의 저항
균형 잡힌 3상 Y 부하에서는 중성 전류가 0이 될 것으로 예상합니다. 자체적으로 중성선을 통해 소스 Y의 공급 단계로 돌아가는 각 상 전류는 모두 동일한 크기이고 모두 120°씩 떨어져 있기 때문에 중성선과 관련하여 서로 상쇄되어야 합니다.
고조파 전류가 없는 시스템에서 이것은 이다 중성 도체를 통해 전류가 0으로 남게 되면 어떻게 됩니까?
그러나 고조파에 대해서는 동일하게 말할 수 없습니다. 동일한 시스템의 전류입니다.
기본 주파수(60Hz 또는 1차 고조파) 전류는 중성 도체에 거의 없습니다. 우리의 푸리에 분석은 Rneutral 양단의 전압을 읽을 때 1차 고조파의 0.4337 µA만 보여줍니다. . 5차 및 7차 고조파에 대해서도 마찬가지이며, 두 전류 모두 무시할 수 있는 크기입니다.
대조적으로, 3차 및 9차 고조파는 중성 도체 내에서 각각 149.3mA(1Ω에 걸쳐 1.493E-01볼트)로 강력하게 나타납니다! 이것은 거의 150mA 또는 개별적으로 전류 소스 값의 3배입니다.
부하의 고조파 주파수당 3개의 소스가 있는 경우 각 위상의 3차 및 9차 고조파 전류가 추가되는 것으로 보입니다. 중성 전류를 형성합니다. 푸리에 분석 참조:"과도 응답 v(0,7)의 푸리에 구성 요소"
이것이 정확히 일어나고 있는 일이지만 왜 그렇게 되었는지는 분명하지 않을 수 있습니다.
이것을 이해하는 열쇠는 위상 전류의 시간 영역 그래프에서 명확하게 알 수 있습니다. 1-2-3의 위상 시퀀스를 사용하여 시간에 따른 균형 위상 전류의 이 플롯을 조사하십시오. (아래 그림)
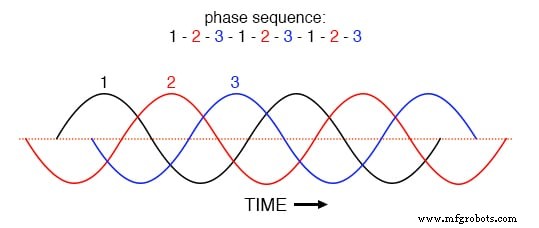
동일한 간격의 파동의 위상 시퀀스 1-2-3-1-2-3-1-2-3.
세 가지 기본 파형이 그래프의 시간 축에 걸쳐 균등하게 이동하면 중성 도체에서 결과 전류가 0이 되도록 서로 상쇄하는 방법을 쉽게 알 수 있습니다. 하지만 1단계의 3차 고조파 파형이 아래 그림의 그래프에 겹쳐서 어떻게 보일지 생각해 보겠습니다.
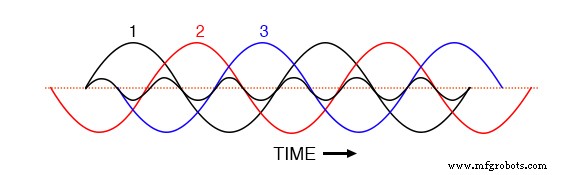
3상 기본 파형에 중첩된 위상 1에 대한 3차 고조파 파형입니다.
이 고조파 파형이 첫 번째와 마찬가지로 두 번째 및 세 번째 기본 파형과 위상 관계가 어떻게 동일한지 관찰합니다. 각 양의 반주기에서 any 기본 파형의 경우 고조파 파형의 정확히 두 개의 양의 반주기와 한 개의 음의 반주기를 찾을 수 있습니다.
이것이 의미하는 바는 3개의 120° 위상 편이된 기본 주파수 파형의 3차 고조파 파형이 실제로 동일한 위상이라는 것입니다. 서로 서로 함께. 3상 AC 시스템에서 일반적으로 가정하는 120°의 위상 변이 수치는 고조파 배수가 아닌 기본 주파수에만 적용됩니다!
동일한 그래프에 3개의 3차 고조파 파형을 모두 표시하면 이 파형이 정확하게 겹치고 단일 통합 파형으로 표시됩니다(아래 그림에서 굵게 표시됨)
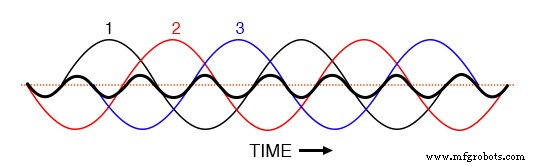
1, 2, 3단계의 3차 고조파는 기본 3상 파형에 중첩될 때 모두 일치합니다.
수학적으로 더 기울어진 사람들을 위해 이 원리는 상징적으로 표현될 수 있습니다. A 하나의 파형을 나타내고 B 다른 하나는 동일한 주파수이지만 위상면에서 서로 120° 이동했습니다. 각 파형의 3차 고조파를 A'라고 합시다. 및 B' , 각각.
A' 사이의 위상 이동 및 B' 120°가 아닙니다(즉, A 사이의 위상 편이입니다. 및 B ) 하지만 3배이므로 A' 및 B' 파형은 A보다 3배 빠르게 번갈아 나타납니다. 및 B . 파형 간의 이동은 위상각으로만 정확하게 표현됩니다. 동일한 각속도를 가정할 때.
다른 주파수의 파형을 연관시킬 때 위상 변이를 나타내는 가장 정확한 방법은 시간; 그리고 타임 시프트 A' 사이 및 B' 3배 낮은 주파수에서 120° 또는 A'의 주파수에서 360°에 해당합니다. 및 B' . 360°의 위상 변이는 위상 변이가 전혀 없는 0°의 위상 변이와 동일합니다.
따라서 A' 및 B' 서로 위상이 같아야 합니다.
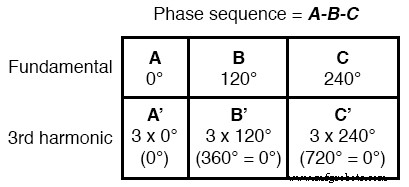
3상 시스템에서 3차 고조파의 이러한 특성은 3차 고조파의 정수 배수에도 적용됩니다.
따라서 각 기본파형의 3차 고조파 파형은 위상이 같을 뿐만 아니라 6차 고조파, 9차 고조파, 12차 고조파, 15차 고조파, 18차 고조파, 21차 고조파 등이 있습니다.
파형 왜곡이 중심선에 대해 대칭이고 대부분의 비선형 부하가 대칭 왜곡을 생성하는 시스템에서는 홀수 고조파만 나타나기 때문에 3차 고조파(6차, 12차, 18차 등)의 짝수 배수는 일반적으로 중요하지 않고 홀수 배수(3번째, 9번째, 15번째, 21번째 등)는 중성 전류에 크게 기여합니다.
3개가 아닌 여러 개의 위상이 있는 다상 전력 시스템에서 이 효과는 동일한 배수의 고조파에서 발생합니다. 예를 들어, 기본 파형 간의 위상 변이가 90°인 별 연결 4상 시스템의 중성 도체에 추가되는 고조파 전류는 4번째, 8번째, 12번째, 16번째, 20번째 등이 됩니다.
3상 전력 시스템에서의 풍부함과 중요성으로 인해 3차 고조파와 그 배수는 3중 고조파라는 고유한 이름을 갖습니다. .
모든 삼중 고조파는 4선 Y 연결 부하의 중성 도체에서 서로 추가됩니다. 상당한 비선형 부하를 포함하는 전력 시스템에서 삼중 고조파 전류는 중성 도체가 과열되도록 하기에 충분히 클 수 있습니다.
이것은 다른 안전 문제로 인해 중성선이 과전류 보호 기능을 갖는 것을 금지하고 따라서 이러한 고전류의 자동 차단에 대한 조항이 없기 때문에 매우 문제가 됩니다.
다음 그림은 부하에서 생성된 3배 고조파 전류가 중성 도체 내에 어떻게 추가되는지 보여줍니다. 기호 "ω"는 각속도를 나타내는 데 사용되며 수학적으로 2πf와 동일합니다. 따라서 "ω"는 기본 주파수를 나타내고 "3ω"는 3차 고조파를 나타내고 "5ω"는 5차 고조파를 나타내는 식입니다. (아래 그림)
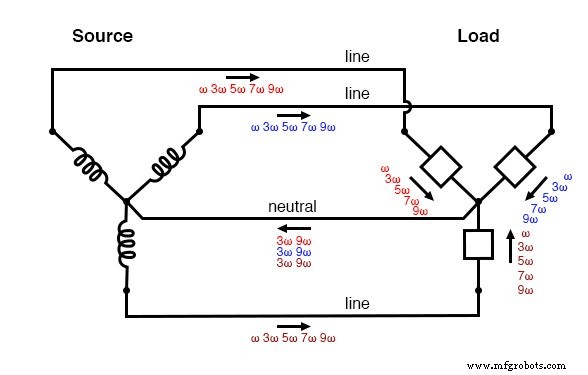
"Y-Y" 삼중 소스/부하:고조파 전류가 중성선에 추가됩니다.
이러한 부가적인 삼중 전류를 완화하기 위해 중성선을 완전히 제거하고 싶을 수 있습니다. 삼중 전류가 함께 흐를 수 있는 중성선이 없으면 그렇지 않겠죠?
Unfortunately, doing so just causes a different problem:the load’s “Y” center-point will no longer be at the same potential as the source’s, meaning that each phase of the load will receive a different voltage than what is produced by the source.
We’ll re-run the last SPICE simulation without the 1 Ω Rneutral resistor and see what happens:
Y-Y source/load (no neutral) with harmonics * * phase1 voltage source and r (120 v / 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v / 120 deg) vsource2 3 0 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v / 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) rsource3 5 6 1 * * line resistances rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 0 0) i5har1 8 7 sin(0 50m 300 0 0) i7har1 8 7 sin(0 50m 420 0 0) i9har1 8 7 sin(0 50m 540 0 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin(0 50m 420 5.55555m 0) i9har2 9 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 11.1111m 0) i5har3 10 7 sin(0 50m 300 11.1111m 0) i7har3 10 7 sin(0 50m 420 11.1111m 0) i9har3 10 7 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 12m 1u .plot tran v(2,8) .four 60 v(2,8) .plot tran v(0,7) .four 60 v(0,7) .plot tran v(8,7) .four 60 v(8,7) .끝
Fourier components of transient response v(2,8) dc component =5.423E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.388E-10 0.000000 158.016 158.016 3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009 4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510 5 3.000E+02 4.990E-02 0.416665 0.000 0.000 6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565 7 4.200E+02 4.990E-02 0.416668 0.000 0.000 8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638 9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005 total harmonic distortion =58.925539 percent
Fourier components of transient response v(0,7) dc component =6.093E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.453E-04 1.000000 60.018 0.000 2 1.200E+02 6.263E-08 0.000431 91.206 31.188 3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018 4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121 5 3.000E+02 3.023E-04 2.080596 119.981 59.963 6 3.600E+02 1.138E-07 0.000783 15.882 -44.136 7 4.200E+02 4.234E-04 2.913955 59.993 -0.025 8 4.800E+02 2.001E-07 0.001378 35.584 -24.434 9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017 total harmonic distortion =************ percent
Fourier components of transient response v(8,7) dc component =6.070E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 0.000 0.000 2 1.200E+02 6.231E-08 0.000000 90.473 90.473 3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000 4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747 5 3.000E+02 9.995E-02 0.000835 179.850 179.850 6 3.600E+02 1.023E-07 0.000000 13.485 13.485 7 4.200E+02 9.959E-02 0.000832 179.790 179.789 8 4.800E+02 1.991E-07 0.000000 35.462 35.462 9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999 total harmonic distortion =59.043467 percent
Strange things are happening, indeed.
First, we see that the triplen harmonic currents (3rd and 9th) all but disappear in the lines connecting a load to source. The 5th and 7th harmonic currents are present at their normal levels (approximately 50 mA), but the 3rd and 9th harmonic currents are of negligible magnitude.
Second, we see that there is a substantial harmonic voltage between the two “Y” center-points, between which the neutral conductor used to connect. According to SPICE, there are 50 volts of both 3rd and 9th harmonic frequency between these two points, which is definitely not normal in a linear (no harmonics), balanced Y system.
Finally, the voltage as measured across one of the load’s phases (between nodes 8 and 7 in the SPICE analysis) likewise shows strong triplen harmonic voltages of 50 volts each.
The figure below is a graphical summary of the aforementioned effects.
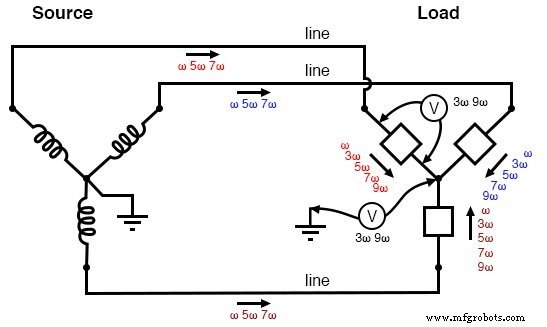
Three-wire “Y-Y” (no neutral) system:Triplen voltages appear between “Y” centers. Triplen voltages appear across load phases. Non-triplen currents appear in line conductors.
In summary, removal of the neutral conductor leads to a “hot” center-point on the load “Y”, and also to harmonic load phase voltages of equal magnitude, all comprised of triplen frequencies.
In the previous simulation where we had a 4-wire, Y-connected system, the undesirable effect from harmonics was excessive neutral current , but at least each phase of the load received voltage nearly free of harmonics.
Since removing the neutral wire didn’t seem to work in eliminating the problems caused by harmonics, perhaps switching to a Δ configuration will. Let’s try a Δ source instead of a Y, keeping the load in its present Y configuration, and see what happens.
The measured parameters will be line current (voltage across Rline , nodes 0 and 8), load phase voltage (nodes 8 and 7), and source phase current (voltage across Rsource , nodes 1 and 2). (아래 그림)
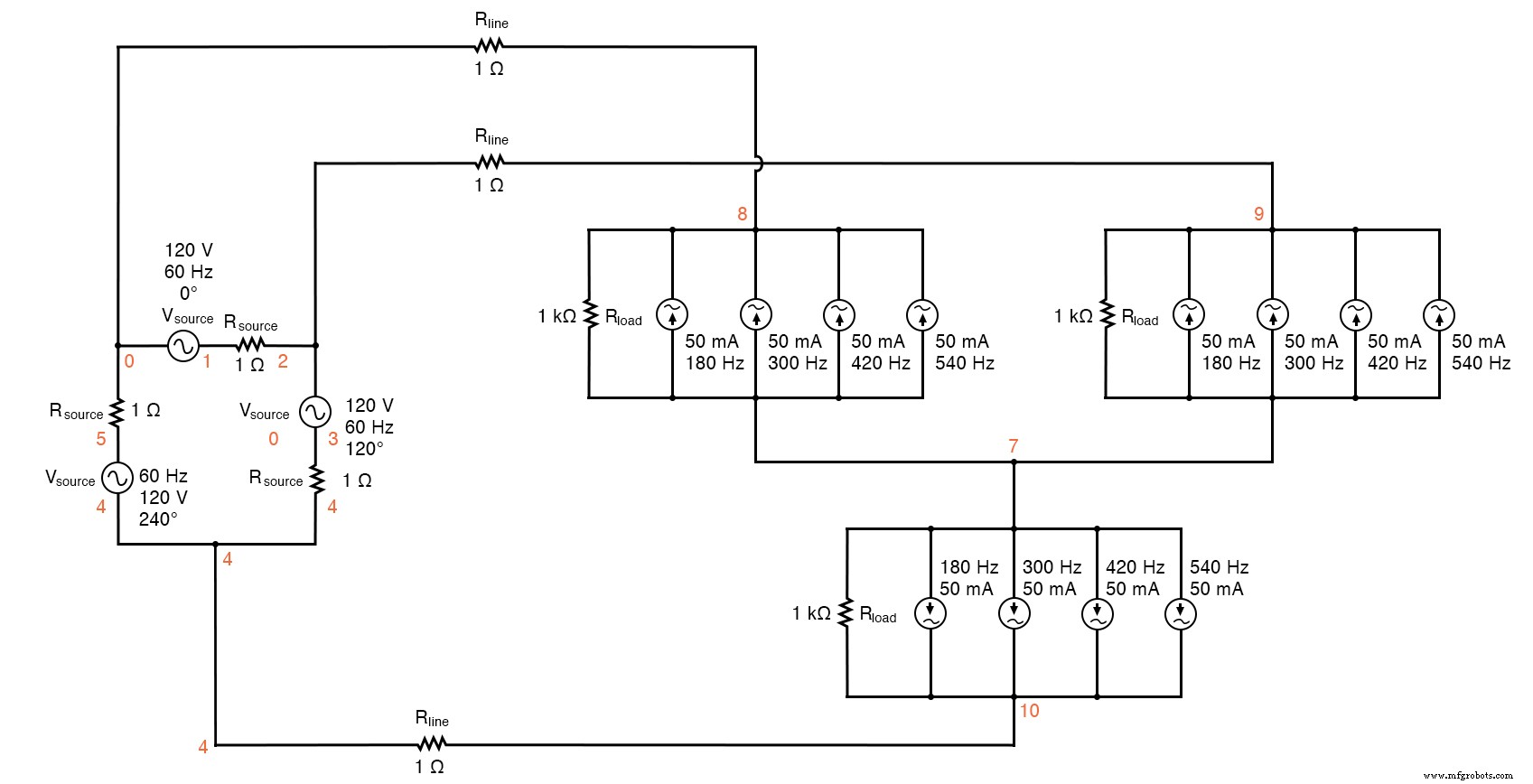
Delta-Y source/load with harmonics
Delta-Y source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 207.846 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 207.846 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 207.846 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 9.72222m 0) i5har1 8 7 sin(0 50m 300 9.72222m 0) i7har1 8 7 sin(0 50m 420 9.72222m 0) i9har1 8 7 sin(0 50m 540 9.72222m 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 15.2777m 0) i5har2 9 7 sin(0 50m 300 15.2777m 0) i7har2 9 7 sin(0 50m 420 15.2777m 0) i9har2 9 7 sin(0 50m 540 15.2777m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 4.16666m 0) i5har3 10 7 sin(0 50m 300 4.16666m 0) i7har3 10 7 sin(0 50m 420 4.16666m 0) i9har3 10 7 sin(0 50m 540 4.16666m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,8) v(8,7) v(1,2) .four 60 v(0,8) v(8,7) v(1,2) .끝
Note:the following paragraph is for those curious readers who follow every detail of my SPICE netlists. If you just want to find out what happens in the circuit, skip this paragraph!
When simulating circuits having AC sources of differing frequency and differing phase, the only way to do it in SPICE is to set up the sources with a delay time or phase offset specified in seconds. Thus, the 0° source has these five specifying figures:“(0 207.846 60 0 0)”, which means 0 volts DC offset, 207.846 volts peak amplitude (120 times the square root of three, to ensure the load phase voltages remain at 120 volts each), 60 Hz, 0 time delay, and 0 damping factor.
The 120° phase-shifted source has these figures:“(0 207.846 60 5.55555m 0)”, all the same as the first except for the time delay factor of 5.55555 milliseconds, or 1/3 of the full period of 16.6667 milliseconds for a 60 Hz waveform.
The 240° source must be time-delayed twice that amount, equivalent to a fraction of 240/360 of 16.6667 milliseconds, or 11.1111 milliseconds.
This is for the Δ-connected source. The Y-connected load, on the other hand, requires a different set of time-delay figures for its harmonic current sources, because the phase voltages in a Y load are not in phase with the phase voltages of a Δ source.
If Δ source voltages VAC, VBA, and VCB are referenced at 0°, 120°, and 240°, respectively, then “Y” load voltages VA, VB, and VC will have phase angles of -30°, 90°, and 210°, respectively.
This is an intrinsic property of all Δ-Y circuits and not a quirk of SPICE. Therefore, when I specified the delay times for the harmonic sources, I had to set them at 15.2777 milliseconds (-30°, or +330°), 4.16666 milliseconds (90°), and 9.72222 milliseconds (210°).
One final note:when delaying AC sources in SPICE, they don’t “turn on” until their delay time has elapsed, which means any mathematical analysis up to that point in time will be in error. Consequently, I set the .tran transient analysis line to hold off analysis until 16 milliseconds after the start, which gives all sources in the netlist time to engage before any analysis takes place.
The result of this analysis is almost as disappointing as the last. (Figure below) Line currents remain unchanged (the only substantial harmonic content being the 5th and 7th harmonics), and load phase voltages remain unchanged as well, with a full 50 volts of triplen harmonic (3rd and 9th) frequencies across each load component.
Source phase current is a fraction of the line current, which should come as no surprise. Both 5th and 7th harmonics are represented there, with negligible triplen harmonics:
Fourier components of transient response v(8,7) dc component =1.259E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 150.000 0.000 2 1.200E+02 1.941E-07 0.000000 49.693 -100.307 3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998 4 2.400E+02 1.519E-07 0.000000 66.397 -83.603 5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E+02 2.433E-07 0.000000 68.162 -81.838 7 4.200E+02 6.931E-02 0.000578 148.548 -1.453 8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E+02 5.000E+01 0.417221 90.006 -59.995 total harmonic distortion =59.004109 percent
Fourier components of transient response v(1,2) dc component =3.564E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 6.906E-02 1.000000 -0.181 0.000 2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E+02 4.267E-06 0.000062 0.006 0.186 total harmonic distortion =59.031969 percent
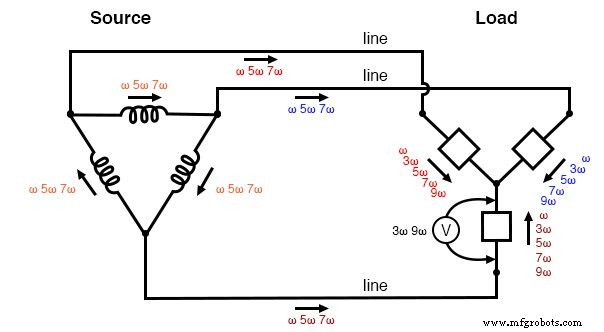
“Δ-Y” source/load:Triplen voltages appear across load phases. Non-triplen currents appear in line conductors and in source phase windings.
Really, the only advantage of the Δ-Y configuration from the standpoint of harmonics is that there is no longer a center-point at the load posing a shock hazard. Otherwise, the load components receive the same harmonically-rich voltages and the lines see the same currents as in a three-wire Y system.
If we were to reconfigure the system into a Δ-Δ arrangement, (Figure below) that should guarantee that each load component receives non-harmonic voltage, since each load phase would be directly connected in parallel with each source phase.
The complete lack of any neutral wires or “center points” in a Δ-Δ system prevents strange voltages or additive currents from occurring.
It would seem to be the ideal solution. Let’s simulate and observe, analyzing line current, load phase voltage, and source phase current. See SPICE listing:“Delta-Delta source/load with harmonics”, “Fourier analysis:Fourier components of transient response v(0,6)”, and “Fourier components of transient response v(2,1)”.
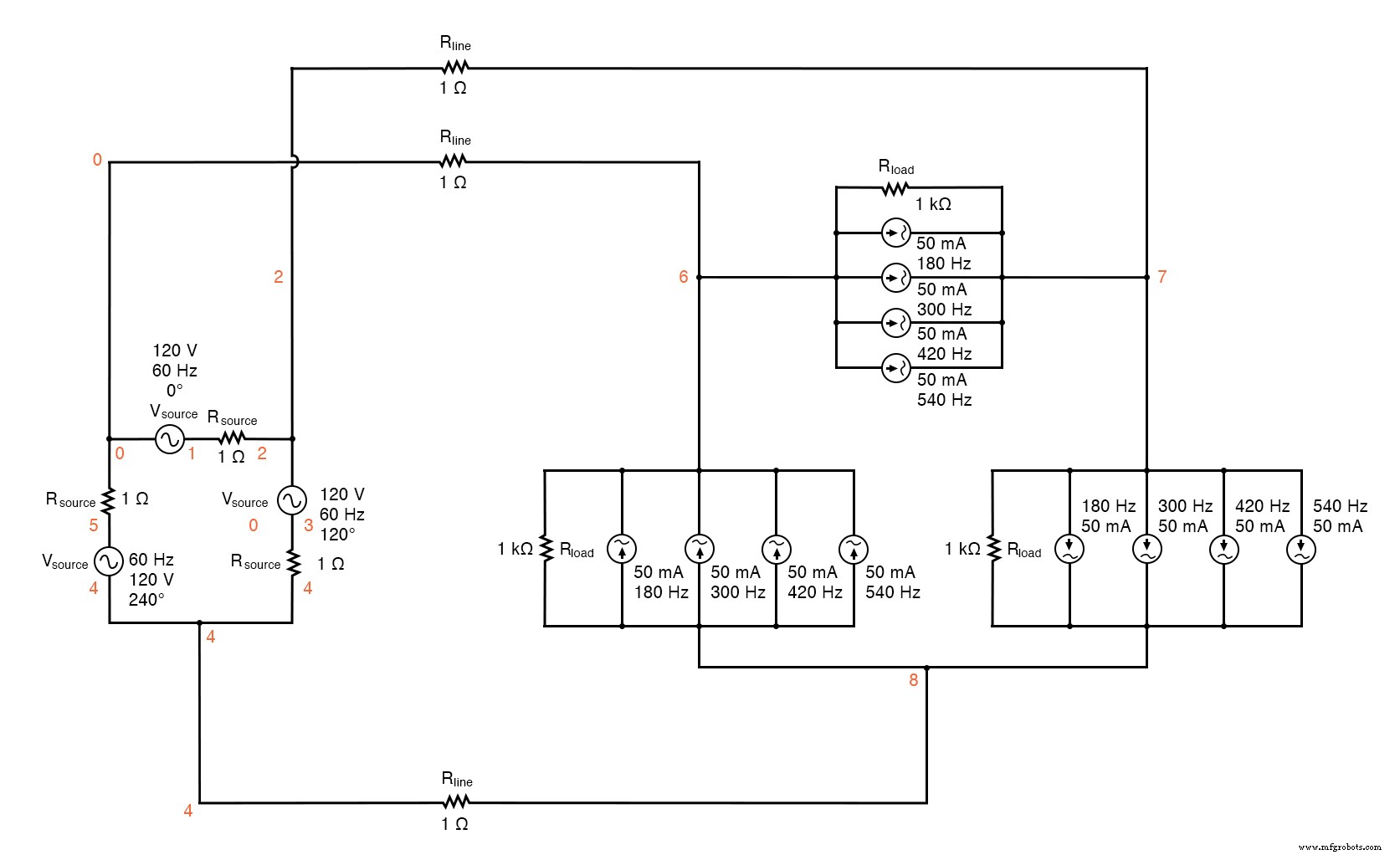
Delta-Delta source/load with harmonics.
Delta-Delta source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 120 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * phase 1 of load rload1 7 6 1k i3har1 7 6 sin(0 50m 180 0 0) i5har1 7 6 sin(0 50m 300 0 0) i7har1 7 6 sin(0 50m 420 0 0) i9har1 7 6 sin(0 50m 540 0 0) * * phase 2 of load rload2 8 7 1k i3har2 8 7 sin(0 50m 180 5.55555m 0) i5har2 8 7 sin(0 50m 300 5.55555m 0) i7har2 8 7 sin(0 50m 420 5.55555m 0) i9har2 8 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 6 8 1k i3har3 6 8 sin(0 50m 180 11.1111m 0) i5har3 6 8 sin(0 50m 300 11.1111m 0) i7har3 6 8 sin(0 50m 420 11.1111m 0) i9har3 6 8 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,6) v(7,6) v(2,1) i(3har1) .four 60 v(0,6) v(7,6) v(2,1) .끝
Fourier components of transient response v(0,6) dc component =-6.007E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 2.070E-01 1.000000 150.000 0.000 2 1.200E+02 5.480E-11 0.000000 156.666 6.666 3 1.800E+02 6.257E-07 0.000003 89.990 -60.010 4 2.400E+02 4.911E-11 0.000000 8.187 -141.813 5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E+02 8.626E-02 0.416669 150.001 0.001 8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E+02 1.877E-06 0.000009 89.987 -60.013 total harmonic distortion =58.925538 percent
Fourier components of transient response v(7,6) dc component =-5.680E-10 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.195E+02 1.000000 0.000 0.000 2 1.200E+02 1.039E-09 0.000000 144.749 144.749 3 1.800E+02 1.251E-06 0.000000 89.974 89.974 4 2.400E+02 4.215E-10 0.000000 36.127 36.127 5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E+02 3.752E-06 0.000000 89.905 89.905 total harmonic distortion =0.235702 percent
Fourier components of transient response v(2,1) dc component =-1.923E-12 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.194E-01 1.000000 179.940 0.000 2 1.200E+02 2.569E-11 0.000000 133.491 -46.449 3 1.800E+02 3.129E-07 0.000003 89.985 -89.955 4 2.400E+02 2.657E-11 0.000000 23.368 -156.571 5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E+02 9.385E-07 0.000008 89.991 -89.949 total harmonic distortion =58.961298 percent
As predicted earlier, the load phase voltage is almost a pure sine-wave, with negligible harmonic content, thanks to the direct connection with the source phases in a Δ-Δ system.
But what happened to the triplen harmonics? The 3rd and 9th harmonic frequencies don’t appear in any substantial amount in the line current, nor in the load phase voltage, nor in the source phase current! We know that triplen currents exist because the 3rd and 9th harmonic current sources are intentionally placed in the phases of the load, but where did those currents go?
Remember that the triplen harmonics of 120° phase-shifted fundamental frequencies are in phase with each other.
Note the directions that the arrows of the current sources within the load phases are pointing, and think about what would happen if the 3rd and 9th harmonic sources were DC sources instead.
What we would have is currently circulating within the loop formed by the Δ-connected phases . This is where the triplen harmonic currents have gone:they stay within the Δ of the load, never reaching the line conductors or the windings of the source.
These results may be graphically summarized as such in the figure below.
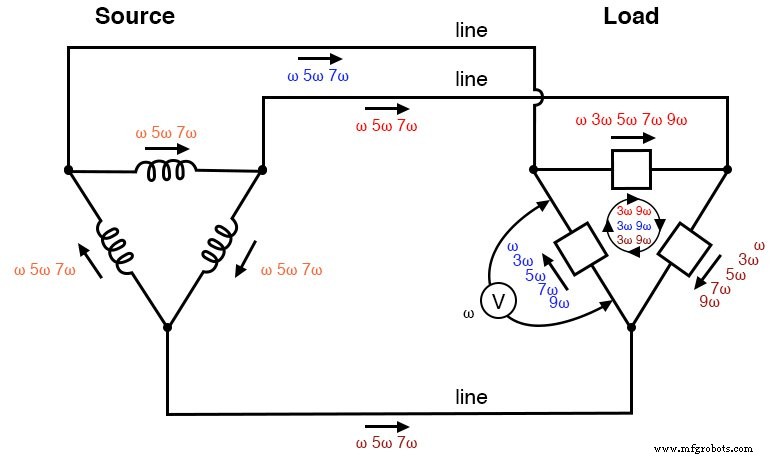
Δ-Δ source/load:Load phases receive undistorted sine wave voltages. Triplen currents are confined to circulate within load phases. Non-triplen currents appear in line conductors and in source phase windings.
This is a major benefit of the Δ-Δ system configuration:triplen harmonic currents remain confined in whatever set of components create them and do not “spread” to other parts of the system.
검토:
<울>관련 워크시트:
<울>산업기술
오늘 기사에서는 과전압 및 그 원인에 대해 알 수 있습니다. 발전기, 변압기 및 전송선과 같은 과전압과 관련된 소스가 너무 많습니다. 이러한 과전압은 낙뢰, 회로 차단기 개방, 도체 접지 등에 의해 발생할 수 있습니다. 이러한 과전압은 크기가 크지 않을 수 있지만 그 영향은 시스템에 연결된 보호 시스템 또는 장치를 중단시킬 수 있습니다. 엔지니어는 항상 작동 유형의 장비에 대한 과전압의 영향을 제한하고 제어하려고 노력합니다. 이제 우리는 과전압의 주요 원인을 찾으려고합니다. 생성될 수 있고 운영 체제에 영향을 미칠 수 있는 방법.
정전은 모든 설정에서 발생할 수 있습니다. 또한 배터리 전압이 필요한 수준 이하로 떨어질 수 있습니다. 이러한 시나리오에서는 배터리 백업이 필수적입니다. 그러나 수많은 산성 배터리를 보유할 수는 없습니다. 대신 안정적인 백업 전원이 필요합니다. 이러한 시나리오에는 무정전 전원 공급 장치(UPS)가 필요합니다. 일정한 입력 전압이 필요한 모든 전자 장비가 계속 작동하도록 합니다. 그러나 UPS 회로는 어떻게 작동합니까? 이에 대해 설명하겠습니다. 실제 주전원을 효과적으로 대체하는 방법에 대해 더 자세히 설명하겠습니다. 따라서 더 많은