산업기술








독일의 물리학자 "Robert Kirchhoff"는 1847년에 두 가지 중요한 전기 법칙을 도입했습니다. 이를 통해 복잡한 네트워크의 등가 저항과 다른 도체의 흐르는 전류를 쉽게 찾을 수 있습니다. AC 및 DC 회로는 모두 Kirchhoff의 전류 법칙(KCL) 및 Kirchhoff의 전압 법칙(KVL)으로 알려진 이러한 간단한 법칙을 사용하여 해결하고 단순화할 수 있습니다.
또한 KCL은 전자기의 전하 연속성 방정식에서 파생되고 KVL은 정적 자기장에 대한 Maxwell – 패러데이 방정식에서 파생됩니다(시간에 대한 B의 도함수는 0 ).
KCL 기준:
모든 전기 네트워크에서 한 지점으로 들어오는 전류와 해당 지점에서 나가는 전류의 대수적 합은 0입니다. 또는 한 지점으로 들어오는 전류는 해당 지점의 나가는 전류와 같습니다.
즉, 한 점으로 흐르는 전류의 합은 그 점에서 멀어지는 전류의 합과 같습니다. 또는 노드에 들어가는 전류의 대수적 합은 노드를 떠나는 전류의 대수적 합과 같습니다.
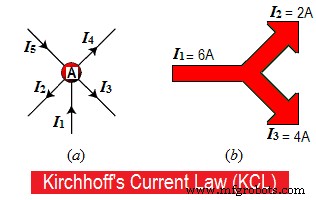
그림 1.a와 같이 일부 도체가 "A" 지점에서 만난다고 가정합니다. 일부 도체에서는 전류가 "A" 지점으로 들어오고 다른 도체에서는 전류가 "A" 지점에서 나가거나 나옵니다.
"A" 지점에서 들어오거나 나가는 전류는 "음(-)"인 반면 들어오거나 들어오는 전류는 "A" 지점에 대해 "양(+)"으로 간주합니다.
다음:
나 1 + (–나 2 ) + (-나 3 ) + (-나 4 ) + 나 5 =0
또는
나 1 + 나 5 – 나 2 – 나 3 – 나 4 =0
또는
나 1 + 나 5 =나 2 + 나 3 + 나 4 =0
즉,
수류 유입 또는 유입 =조류 유출 또는 유출
또는
Σ나 입력 =Σ나 출발
예를 들어 그림 1.b에서 8A는 한 점을 향해 다가오고 5A와 3A는 그 점을 떠나고 있으므로
8A =5A + 3A
8A =8A.
Kirchhoff의 두 번째 법칙 또는 KVL은 다음과 같이 명시했습니다.
즉, 모든 폐쇄 루프(메시라고도 함)에서 적용된 EMF의 대수적 합은 요소의 전압 강하의 대수적 합과 같습니다. . Kirchhoff의 두 번째 법칙은 전압 법칙 또는 메시 법칙이라고도 합니다.
ΣIR=ΣE
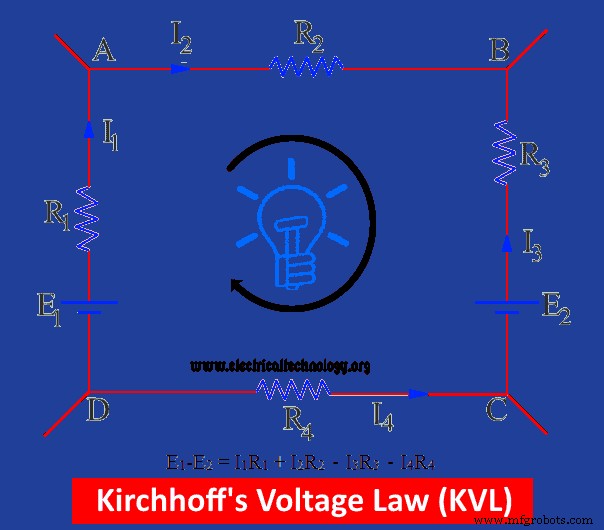
배터리 E1의 두 연결을 포함하는 폐쇄 회로가 그림에 나와 있습니다. 및 E2 . 배터리의 E.M.F의 전체 합계는 E1로 표시됩니다. -E2 . 전류의 가상 방향도 그림에 나와 있습니다.
E1 E2 동안 양의 방향으로 전류를 구동합니다. 전류 방향으로 간섭하므로(즉, 가정된 전류 방향의 반대 방향임) 음수로 간주됩니다. 이 폐쇄 회로의 전압 강하는 전압과 전류의 곱에 따라 달라집니다.
가상 전류 방향으로 발생하는 전압 강하는 양의 전압 강하, 다른 하나는 음의 전압 강하로 알려져 있습니다.
위의 그림에서 나는1 R1 그리고 나2 R2 양의 전압 강하 및 I3 R3 그리고 나4 R4 음수 V.D.
폐쇄 회로(또는 각 메쉬)를 둘러보고 도체의 저항과 그 안에 흐르는 전류를 곱하면 IR의 합은 다음과 같습니다. 회로에 연결된 적용된 EMF 소스의 합계입니다.
위 회로의 전체 방정식은 다음과 같습니다.
E1 – E2 =나 1 R1 + 나 2 R2 – 나 3 R3 – 나 4 R4
그림과 같이 전류의 가정된 방향으로 가면 IR의 곱은 양의 값이 아닌 음의 값으로 간주됩니다.
알아두면 좋은 정보:
전류 방향:
키르히호프의 법칙을 통해 회로를 풀 때 전류의 방향을 결정하는 것은 매우 중요합니다. 선거 현재와 재래식의 경우와 동일합니다.
전류의 방향은 시계 방향 또는 반시계 방향을 통해 가정할 수 있습니다. 전류의 사용자 지정 방향을 선택하면 회로의 최종 솔루션이 될 때까지 전체 회로에 대해 동일한 방향을 적용하고 유지해야 합니다.
최종 값이 양수이면 전류의 예상 방향이 정확하다는 의미입니다. 음수 값의 경우 방향의 전류가 그때와 비교하여 반전됩니다.
KCL 및 KVL(Kirchhoff의 법칙)에 대한 해결 예
예:
R1의 저항기 =10Ω, R2 =4Ω 및 R3 =8Ω은 그림과 같이 최대 2개의 배터리(저항이 무시할 수 있는 수준)에 연결됩니다. 각 저항에 흐르는 전류를 찾으십시오. 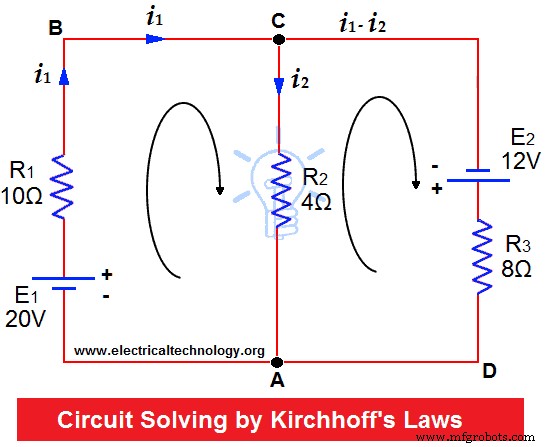
해결책:
화살표로 표시된 방향으로 전류가 흐른다고 가정합니다.
접점 C 및 A에 KCL을 적용합니다.
따라서 현재 메쉬 ABC =i 1
메시 CA의 현재 =i 2
현재 Mesh CDA =i 1 – 나 2
이제 Mesh ABC에 KVL을 적용하면 20V가 시계 방향으로 작동합니다. IR 제품의 합계를 동일하게 하면 다음을 얻습니다.
10i 1 + 4나 2 =20 ... (1)
메시 ACD에서 12볼트가 시계 방향으로 작용하면 다음과 같습니다.
8(i 1 – 나 2 ) – 4나 2 =12
8i 1 – 8나 2 – 4나 2 =12
8i 1 – 12나 2 =12 ... (2)
방정식(1)에 3을 곱하기
30i 1 + 12나 2 =60
i 해결 1
30i 1 + 12나 2 =60
8i 1 – 12나 2 =12
___________
38i 1 =72
위의 방정식은 Elimination 또는 Cramer의 법칙으로 단순화할 수도 있습니다.
나는 1 =72 ÷ 38 =1.895암페어 =10옴 저항의 전류
이 값을 (1)에 대입하면 다음을 얻습니다.
10(1.895) + 4i 2 =20
4i 2 =20 – 18.95
나는 2 =0.263 암페어 =4옴 저항의 전류
지금,
나는 1 – 나 2 =1.895 – 0.263 =1.632 암페어
알아두면 좋은 정보:
Kirchhoff의 법칙에 따라 전기 회로를 단순화하고 분석할 때 이러한 경험 법칙을 고려해야 합니다.
전기 회로 분석 정리에 대한 관련 게시물:
산업기술
전압 조정기 일종의 전압 조정기가 필요하지 않은 전기 제품은 거의 없습니다. 그리고 이러한 사실은 전압 조정기를 회로에 가장 많이 사용되는 전기 부품 중 하나로 만듭니다. 코스에서 배터리 전압 또는 DC/AC 어댑터 전압을 직접 소모할 수 없는 경우 전류 증가 및 순간 전류로 인한 손상을 방지하기 위해 전압 조정기가 필요합니다. 또한 회로를 선택하거나 만들기 전에 고전류 전압 조정기에 대해 잘 이해해야 합니다. 따라서 이 기사에서는 고전류 전압 조정기의 작동 방식, 전압 조정기 유형, 애플리케이션 및 프로젝트를 위해 구축할 수
전류 조절기는 휴대폰을 충전하거나, 자동차에 시동을 걸거나, 컴퓨터를 꽂거나, 작은 전기 제품을 켤 때마다 작동합니다. 전압 조정기라고도 하는 전류 조정기는 전기 장치가 작동하는 데 필요한 수준으로 전기량을 줄이고 제한합니다. 미국(미국)의 표준 주택 전류는 110볼트이며, 이는 영국 및 대부분의 유럽 국가에서 240볼트입니다. 그러나 많은 전기 장치는 들어오는 전압의 일부만 필요로 합니다. 여기에서 전류 조정기가 작동합니다. 일반적으로 전류 조정기는 정해진 양의 전류만 장치에 통과할 수 있도록 하는 강압 변압기의 한 형태입니다.