산업기술








인버터와 버퍼는 단일 입력 게이트 회로의 가능성을 소진시킵니다. 단일 논리 신호로 버퍼링하거나 반전시키는 것 외에 무엇을 더 할 수 있습니까? 더 많은 논리 게이트 가능성을 탐색하려면 회로에 더 많은 입력 단자를 추가해야 합니다.
논리 게이트에 더 많은 입력 단자를 추가하면 입력 상태 가능성의 수가 증가합니다. 인버터나 버퍼와 같은 단일 입력 게이트의 경우 가능한 입력 상태는 두 가지뿐입니다. 입력이 "높음"(1)이거나 "낮음"(0)입니다.
이 장의 앞부분에서 언급했듯이 2개의 입력 게이트에는 4 가능성(00, 01, 10 및 11). 3입력 게이트는 8 입력 상태에 대한 가능성(000, 001, 010, 011, 100, 101, 110 및 111).
가능한 입력 상태의 수는 2의 입력 수의 거듭제곱과 같습니다.

가능한 입력 상태 수의 이러한 증가는 분명히 더 복잡한 게이트 동작을 허용합니다. 이제 단일 "높음" 또는 "낮음" 논리 레벨을 단순히 반전 또는 증폭(버퍼링)하는 대신 게이트의 출력은 조합에 따라 결정됩니다. 입력 단자에 1과 0이 존재합니다.
단지 몇 개의 입력 단자로 많은 조합이 가능하기 때문에 인버터나 버퍼만 될 수 있는 단일 입력 게이트와 달리 다중 입력 게이트에는 다양한 유형이 있습니다. 각 기본 게이트 유형은 표준 기호, 진리표 및 실제 작동을 보여주는 이 섹션에서 제공됩니다. 이러한 다양한 게이트의 실제 TTL 회로는 다음 섹션에서 살펴보겠습니다.
이해하기 가장 쉬운 다중 입력 게이트 중 하나는 AND 게이트입니다. 이 게이트의 출력은 모두 입력(첫 번째 입력 및 두 번째 입력 및 . . .) "높음"(1)입니다. 입력이 "낮음"(0)이면 출력도 "낮음" 상태가 됩니다.

AND 게이트는 3개 이상의 입력으로 만들어지지만 이것은 단순한 2개 입력보다 덜 일반적입니다.
2입력 AND Gate의 진리표
2입력 AND 게이트의 진리표는 다음과 같습니다.
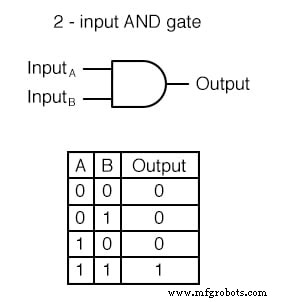
AND 게이트 샘플 회로 작동
이 진리표가 실제적으로 의미하는 바는 2-입력 AND 게이트가 입력 논리 레벨의 모든 가능성에 종속되는 다음 그림 시퀀스에 표시됩니다. LED(Light-Emitting Diode)는 출력 로직 레벨을 시각적으로 표시합니다.
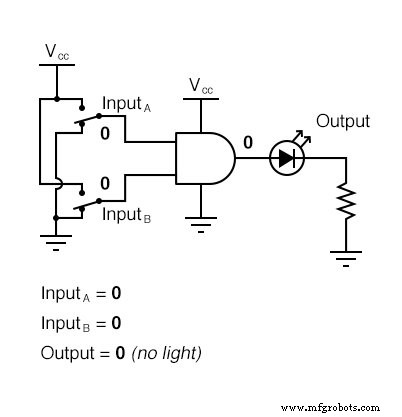
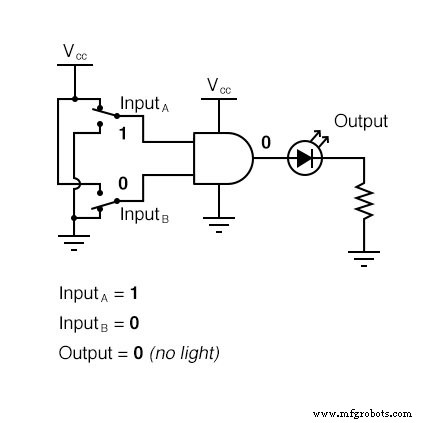
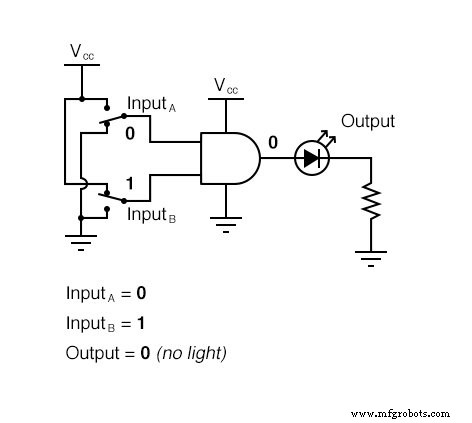
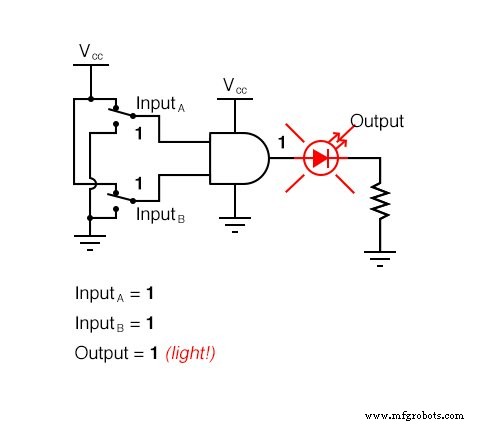
AND 게이트의 출력이 "높음"이 되는 것은 모든 입력이 "높음" 논리 레벨로 올라갔을 때만 가능하므로 4개의 입력 조합 상태 중 하나만에 대해 LED를 활성화합니다.
AND 게이트 아이디어의 변형을 NAND 게이트라고 합니다. "NAND"라는 단어는 NOT과 AND의 축약어입니다.
기본적으로 NAND 게이트는 출력 단자에 연결된 NOT(인버터) 게이트가 있는 AND 게이트와 동일하게 동작합니다. 이 출력 신호 반전을 상징하기 위해 NAND 게이트 기호는 출력 라인에 거품이 있습니다.
NAND 게이트의 진리표는 예상한 대로 AND 게이트의 진리표와 정반대입니다.
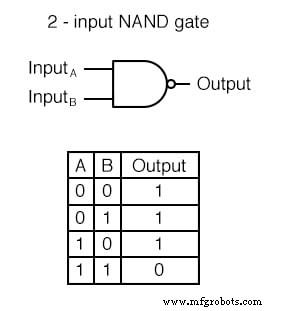
AND 게이트와 마찬가지로 NAND 게이트는 두 개 이상의 입력으로 만들어집니다. 이러한 경우 동일한 일반 원칙이 적용됩니다. 모든 입력이 "높음"(1)인 경우에만 출력이 "낮음"(0)이 됩니다. 입력이 "낮음"(0)이면 출력은 "높음"(1)이 됩니다.
조사할 다음 게이트는 OR 게이트입니다. 왜냐하면 입력(첫 번째 입력 또는 두 번째 입력 또는 ...) 중 하나라도 "높음"(1)인 경우 이 게이트의 출력이 "높음"(1)이 되기 때문입니다. ). OR 게이트의 출력은 모든 입력이 "로우"(0)인 경우에만 "로우"(0)가 됩니다.

2입력 OR 게이트 진리표
2입력 OR 게이트의 진리표는 다음과 같습니다.
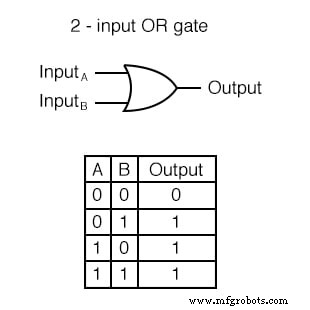
OR 게이트 샘플 회로 작동
다음 그림 시퀀스는 가능한 모든 논리 수준을 경험하는 2-입력과 함께 OR 게이트의 기능을 보여줍니다. LED(Light-Emitting Diode)는 게이트의 출력 로직 레벨을 시각적으로 표시합니다.
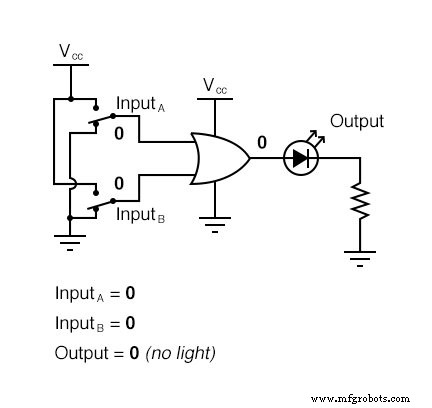
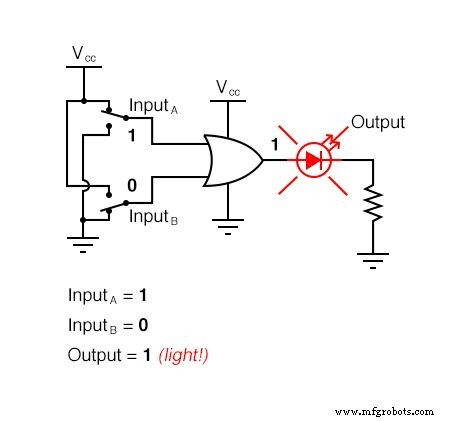
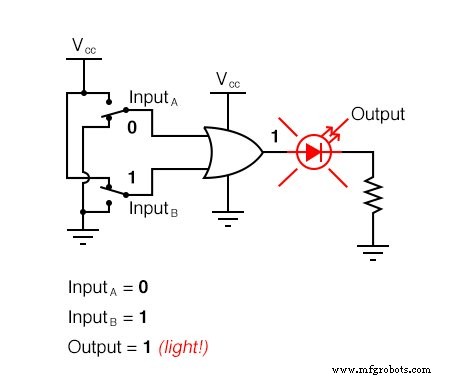
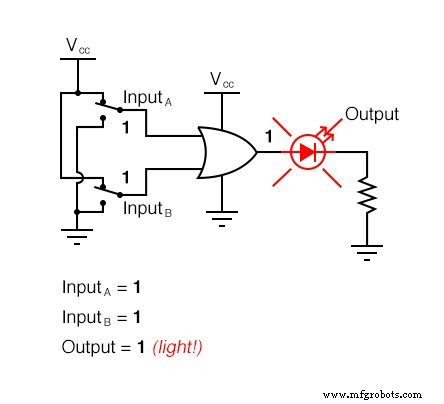
입력이 "하이" 논리 레벨로 올라가는 조건은 OR 게이트의 출력이 "하이"가 되도록 하여 4개의 입력 조합 상태 중 3개에 대해 LED를 활성화합니다.
예상하셨겠지만, NOR 게이트는 출력이 반전된 OR 게이트이며, NAND 게이트는 출력이 반전된 AND 게이트입니다.
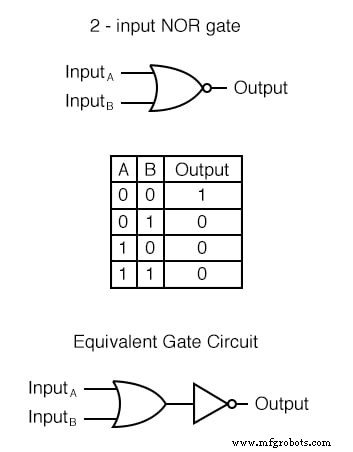
지금까지 본 다른 모든 다중 입력 게이트와 마찬가지로 NOR 게이트는 2개 이상의 입력으로 제조할 수 있습니다. 여전히 동일한 논리 원리가 적용됩니다. 입력 중 하나라도 "높음"(1)으로 설정되면 출력이 "낮음"(0)이 됩니다. 모든 입력이 "낮음"(0)일 때만 출력이 "높음"(1)입니다.
네거티브 AND 게이트는 모든 입력이 반전된 AND 게이트와 동일하게 작동합니다(NOT 게이트를 통해 연결됨). 표준 게이트 기호 규칙에 따라 이러한 반전된 입력은 거품으로 표시됩니다.
대부분의 사람들의 첫 번째 본능과 달리 Negative-AND 게이트의 논리적 동작은 NAND 게이트와 동일하지 않습니다. 진리표는 실제로 NOR 게이트와 동일합니다.
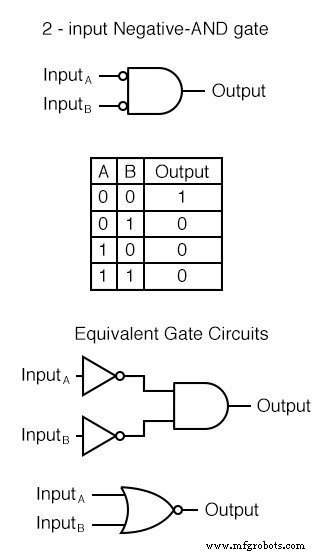
동일한 패턴에 따라 Negative-OR 게이트는 모든 입력이 반전된 OR 게이트와 동일하게 기능합니다. 표준 게이트 기호 규칙에 따라 이러한 반전된 입력은 거품으로 표시됩니다. Negative-OR 게이트의 동작 및 진리표는 NAND 게이트와 동일합니다.
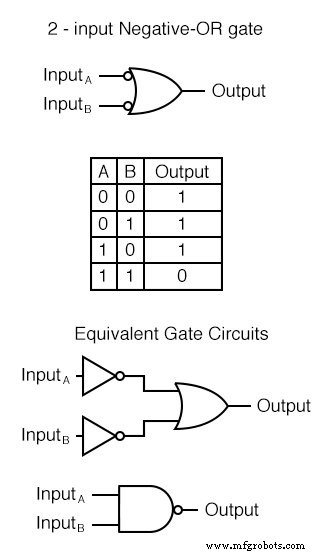
마지막 6가지 게이트 유형은 모두 AND, OR 및 NOT의 세 가지 기본 기능에 대한 상당히 직접적인 변형입니다. 그러나 Exclusive-OR 게이트는 완전히 다릅니다.
배타적 논리합 게이트는 입력이 서로 다른 논리 레벨(0과 1 또는 1과 0)에 있는 경우 "높은"(1) 논리 수준을 출력합니다. 반대로 입력이 다음과 같은 경우 "낮은"(0) 논리 수준을 출력합니다. 동일한 논리 수준입니다.
배타적 논리합(XOR이라고도 함) 게이트에는 고유한 기호와 진리표 패턴이 모두 있습니다.
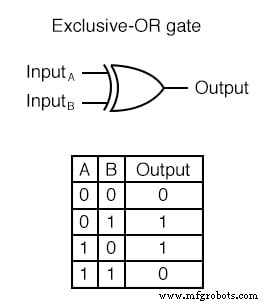
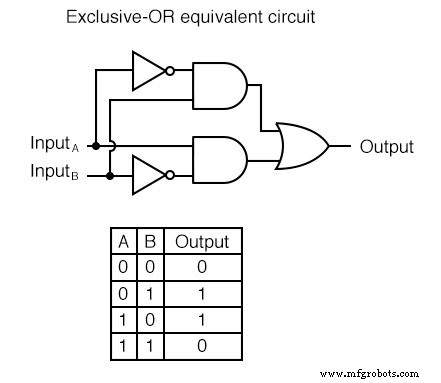
XOR 등가 회로
AND, OR 및 NOT 게이트로 구성된 배타적 논리합 게이트에 대한 등가 회로가 있으며, NAND, NOR 및 음수 입력 게이트가 있습니다. Exclusive-OR 게이트를 시뮬레이션하는 다소 직접적인 접근 방식은 일반 OR 게이트로 시작한 다음 두 입력이 모두 "하이"(1)일 때 출력이 "하이"(1)가 되는 것을 방지하기 위해 추가 게이트를 추가하는 것입니다.
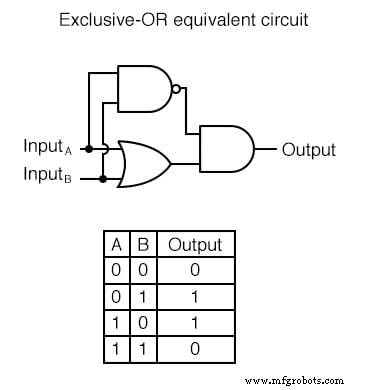
이 회로에서 마지막 AND 게이트는 NAND 게이트의 출력이 높을 때마다 OR 게이트의 출력을 위한 버퍼 역할을 합니다. 이는 처음 세 개의 입력 상태 조합(00, 01, 10)에 대한 것입니다. 그러나 두 입력이 모두 "높음"(1)이면 NAND 게이트는 "낮음"(0) 논리 레벨을 출력하여 최종 AND 게이트가 "낮음"(0) 출력을 생성하도록 합니다.
Exclusive-OR 게이트의 또 다른 등가 회로는 입력 조건 01 및 10에 대해 "높은"(1) 출력을 생성하도록 설정된 인버터가 있는 두 개의 AND 게이트 전략을 사용합니다. 그런 다음 최종 OR 게이트는 AND 게이트 중 하나를 허용합니다. high" 출력을 생성하여 최종 "high" 출력 생성:
배타적 논리합 게이트는 두 개 이상의 이진수를 비트 단위로 비교해야 하는 회로와 오류 감지(패리티 검사) 및 코드 변환(이진에서 회색으로 또는 그 반대로)에 매우 유용합니다.
마지막으로 분석을 위한 마지막 게이트는 XNOR 게이트라고도 하는 Exclusive-NOR 게이트입니다. 출력이 반전된 Exclusive-OR 게이트와 동일합니다. 이 게이트의 진리표는 배타적 논리합 게이트의 진리표와 정확히 반대입니다.
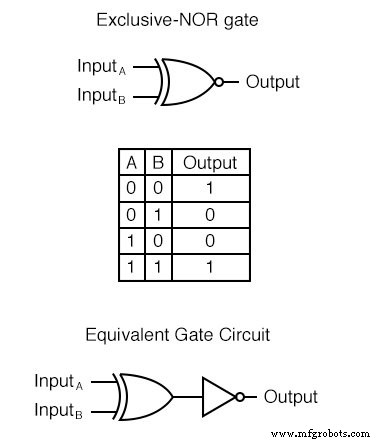
진리표에서 알 수 있듯이 Exclusive-NOR 게이트의 목적은 두 입력이 동일한 논리 레벨(00 또는 11)에 있을 때마다 "높은"(1) 논리 레벨을 출력하는 것입니다.
검토:
<울>
관련 워크시트:
<울>부울 대수학 워크시트
산업기술
기존 사이리스터 장치의 구동(게이트 트리거 전류) 요구 사항을 줄이기 위해 설계된 비교적 최근의 두 가지 기술은 MOS 게이트 사이리스터와 MOS 제어 사이리스터(MCT)입니다. MOS 게이트 사이리스터 MOS 게이트 사이리스터는 MOSFET을 사용하여 표준 사이리스터 구조의 상위(PNP) 트랜지스터를 통해 전도를 시작하여 장치를 트리거합니다. MOSFET은 구동하기 위해 무시할 수 있는 전류가 필요하기 때문에(포화하게 함) 사이리스터를 전체적으로 트리거하기가 매우 쉽습니다. (아래 그림) MOS 게이트 사이리스터 등
디지털 시스템은 인간 기술의 정점에 있습니다. 이러한 시스템에는 일반적으로 정보를 디지털 형식으로 저장, 처리 및 전달하는 마이크로컨트롤러 또는 컴퓨터가 포함됩니다. 그러나 그것이 모든 것의 표면입니다. 디지털 회로는 2진수 형식인 1과 0으로 정보를 교환합니다. 또한 논리 게이트는 오늘날 우리가 가지고 있는 대량의 디지털 논리 회로를 만든 토대를 마련합니다. 그러나 기본 논리 게이트 진리표에 대해 더 깊이 이해하려면 부울 논리에 익숙해야 합니다. 운 좋게도 우리는 논리 게이트, 이진 입력, 논리 연산 및 입력 조합에 대한