전압 및 전류 계산

시간이 지남에 따라 무효 DC 회로의 값을 계산하는 확실한 방법이 있습니다.

반응성 DC 회로의 값 계산

첫 번째 단계는 커패시터 또는 인덕터가 변화에 반대하는 양에 대한 시작 및 최종 값을 식별하는 것입니다. 즉, 반응성 구성 요소가 일정하게 유지하려고 하는 양입니다. 커패시터의 경우 이 양은 전압입니다.; 인덕터의 경우 이 수량은 현재입니다. . 회로의 스위치가 닫히거나 열리면 리액티브 구성 요소는 해당 수량을 스위치 전환 전과 동일한 수준으로 유지하려고 시도하므로 해당 값이 "시작" 값에 사용됩니다.

이 양의 최종 값은 무한한 시간 후에 해당 양이 무엇이든 됩니다. 이것은 커패시터가 개방 회로인 것처럼 용량성 회로를 분석하고 인덕터가 단락된 것처럼 유도성 회로를 분석함으로써 결정할 수 있습니다. 왜냐하면 이러한 구성요소가 "완전 충전"에 도달했을 때와 같이 동작하기 때문입니다. 무한한 시간 후에.

다음 단계는 시간 상수를 계산하는 것입니다. 회로의:전압 또는 전류 값이 과도 상황에서 시작 값에서 최종 값으로 약 63% 변경되는 데 걸리는 시간입니다.

직렬 RC 회로에서 시간 상수는 옴 단위의 총 저항에 패럿 단위의 총 커패시턴스를 곱한 것과 같습니다. 직렬 L/R 회로의 경우 헨리 단위의 총 인덕턴스를 옴 단위의 총 저항으로 나눈 값입니다. 두 경우 모두 시간 상수는 초 단위로 표시됩니다. 그리스 문자 "tau"(τ)로 상징됨:

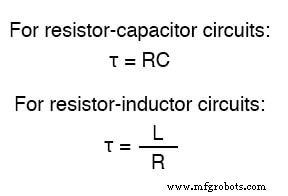
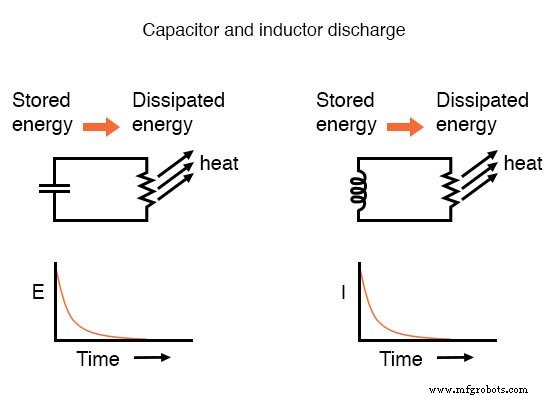
과도 현상에 대한 응답으로 전압 및 전류와 같은 회로 값의 상승 및 하강은 앞에서 언급한 바와 같이 점근적입니다. . 따라서 값은 과도 직후에 급격히 변화하기 시작하고 시간이 지남에 따라 안정됩니다. 그래프에 그리면 전압과 전류의 최종 값에 대한 접근이 지수 곡선을 형성합니다.

이전에 언급했듯이 하나의 시간 상수는 이러한 값이 시작 값에서 (궁극) 최종 값으로 약 63% 변경되는 데 걸리는 시간입니다. 모든 시간 상수에 대해 이러한 값은 최종 목표에 (약) 63% 더 가깝게 이동합니다. 정확한 백분율을 결정하는 수학 공식은 매우 간단합니다.

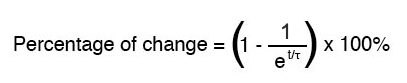
문자 e 오일러 상수를 나타내며 약 2.7182818입니다. 회로 값의 점근적 접근 방식을 수학적으로 분석한 후 미적분 기술에서 파생됩니다. 시간 상수의 가치가 있는 시간 후 시작 값에서 최종 값으로의 변경 비율은 다음과 같습니다.

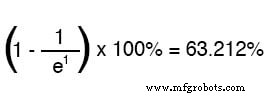
두 개의 시간 상수에 해당하는 시간 후 시작 값에서 최종 값으로의 변화 비율은 다음과 같습니다.

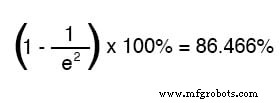
10개의 시상수 시간 후 백분율은 다음과 같습니다.

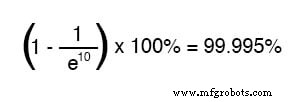
배터리의 일시적인 전압 적용 이후 시간이 지날수록 분수의 분모 값이 커지고 전체 분수에 대한 값이 작아지므로 총계(1 빼기 분수)가 가까워집니다. 1 또는 100%입니다.

범용 시간 상수 공식

이 양에 최종 회로 값과 시작 회로 값의 차이를 곱하여 과도 회로의 전압 및 전류 값을 결정하기 위해 이 공식에서 보다 보편적인 공식을 만들 수 있습니다.

이 장의 시작 부분에 표시된 직렬 저항-커패시터 회로의 전압 상승을 분석해 보겠습니다.

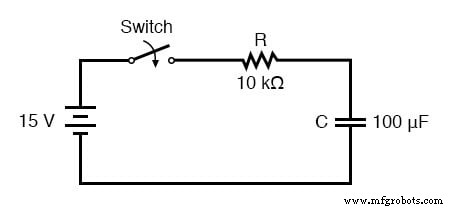
전압을 분석하기로 선택한 것은 커패시터가 일정하게 유지되는 경향이 있기 때문입니다. 공식은 전류에 대해 잘 작동하지만 전류의 시작 및 최종 값은 실제로 커패시터의 전압에서 파생되므로 전압을 계산하는 것이 보다 직접적인 방법입니다. 저항은 10kΩ이고 커패시턴스는 100μF(마이크로패럿)입니다. RC 회로의 시정수(τ)는 저항과 커패시턴스의 곱이므로 1초의 값을 얻습니다.

커패시터가 완전히 방전된 상태(0볼트)에서 시작하면 해당 전압 값을 "시작" 값으로 사용할 수 있습니다. 물론 최종 값은 배터리 전압(15볼트)입니다. 이 회로의 커패시터 전압에 대한 보편적인 공식은 다음과 같습니다.

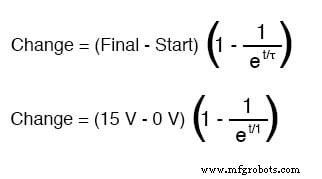
따라서 닫힌 스위치를 통해 전압을 인가하고 7.25초 후에 커패시터 전압은 다음과 같이 증가합니다.

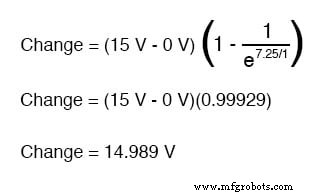
0볼트의 커패시터 전압에서 시작했기 때문에 이 14.989볼트의 증가는 7.25초 후에 14.989볼트가 됨을 의미합니다.

동일한 공식이 해당 회로의 전류를 결정하는 데에도 적용됩니다. 방전된 커패시터가 처음에는 단락 회로처럼 작동한다는 것을 알고 있기 때문에 시작 전류는 가능한 최대량입니다. 15볼트(배터리에서)를 10kΩ으로 나눈 값(처음에는 회로의 전류에 대한 유일한 반대):

우리는 또한 커패시터가 결국에는 개방 회로처럼 동작하기 때문에 최종 전류가 0이 될 것이라는 것도 알고 있습니다. 이는 결국 회로에 전자가 흐르지 않는다는 것을 의미합니다. 이제 시작 전류 값과 최종 전류 값을 모두 알았으므로 범용 공식을 사용하여 동일한 RC 회로에서 7.25초의 스위치 폐쇄 후 전류를 결정할 수 있습니다.

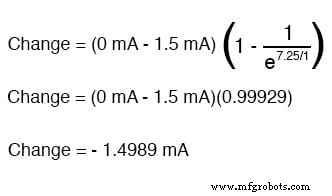
변화에 대해 얻은 수치는 양수가 아니라 음수입니다! 이것은 전류가 감소 했음을 알려줍니다. 시간이 지남에 따라 증가하기 보다는. 1.5mA의 전류에서 시작했기 때문에 이 감소(-1.4989mA)는 7.25초 후에 0.001065mA(1.065μA)가 됨을 의미합니다.

우리는 또한 10kΩ 저항기 양단의 전압 강하를 얻기 위해 배터리 전압(15볼트)에서 커패시터 전압(14.989볼트)을 뺀 다음 저항기(및 전체 직렬 회로) 옴의 법칙(I=E/R). 어느 쪽이든 동일한 답변을 얻어야 합니다.

유도 회로 분석을 위한 세계 시상수 공식 사용

보편적인 시간 상수 공식은 유도 회로 분석에도 잘 작동합니다. 장의 시작 부분에 있는 예제 L/R 회로에 적용해 보겠습니다.

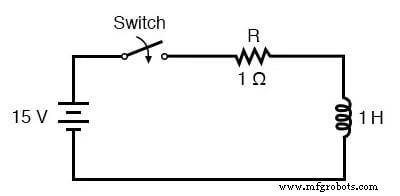
1 헨리의 인덕턴스와 1 Ω의 직렬 저항에서 우리의 시간 상수는 1초와 같습니다.

이것은 유도 회로이고 인덕터가 전류 변화에 반대한다는 것을 알고 있기 때문에 전류의 시작 및 최종 값에 대한 시간 상수 공식을 설정할 것입니다. 열린 위치의 스위치로 시작하면 전류는 0과 같으므로 0은 시작 전류 값입니다.

스위치가 오랫동안 닫힌 상태로 유지되면 전류는 소스 전압을 전체 회로 저항(I=E/R)으로 나눈 값과 동일한 최종 값으로 안정화되거나 이 회로의 경우 15암페어가 됩니다. .

3.5초에서 전류 값을 결정하려면 다음과 같은 범용 시정수 공식을 적용합니다.

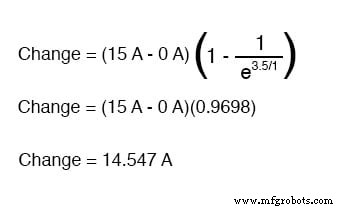
시작 전류가 0이라는 사실을 감안할 때 3.5초의 시간에 14.547A의 회로 전류가 남습니다.

유도성 회로의 전압을 결정하는 것은 먼저 회로 전류를 파악한 다음 저항에 걸친 전압 강하를 계산하여 인덕터에 남은 전압 강하를 찾는 방법으로 가장 잘 수행됩니다. 예제 회로에서 단 하나의 저항(1Ω 값을 가짐)으로 이것은 다소 쉽습니다.

15볼트의 배터리 전압에서 빼면 시간=3.5초에서 인덕터에 0.453볼트가 남습니다.

검토:

<울>

범용 시간 상수 공식:

RC 또는 L/R 회로를 분석하려면 다음 단계를 따르십시오.

(1):회로(RC 또는 L/R)의 시정수를 결정합니다.

(2):계산할 양을 식별합니다(변화가 무효 성분에 의해 직접 반대되는 양. 커패시터의 경우 전압, 인덕터의 경우 전류).

(3):해당 수량의 시작 및 최종 값을 결정합니다.

(4):이 모든 값(최종, 시작, 시간, 시간 상수)을 보편적 시간 상수 공식에 연결하고 변화를 구합니다. 수량입니다.

(5):시작 값이 0이면 지정된 시간의 실제 값은 범용 공식에 의해 주어진 계산된 변화와 같습니다. 그렇지 않은 경우 시작 값에 변경 사항을 추가하여 현재 위치를 찾으십시오.

관련 워크시트:

<울>

시간 상수 회로 워크시트

시간 상수 계산 워크시트

저희 컬렉션 보기 전력 계산기 도구 섹션.