메쉬 분석이란:절차 및 예

전자 분야에서는 간단한 회로도 분석하는 것이 더 중요합니다. 간단한 회로의 분석에는 Kirchhoff의 전압 및 Kirchhoff의 전류 법칙과 같은 원리가 사용됩니다. 여러 제어 전압 및 전류 소스가 있는 복잡한 회로의 상황에서는 KVL 및 KCL 법칙과 함께 추가 도구가 있어야 합니다. KVL 및 KCL 원칙에서만 분석이 부정확하고 신뢰할 수 없는 것으로 판명되었습니다. 따라서 정확한 분석을 진행하고 해당 회로의 변수를 알기 위해서는 메쉬 및 노드와 같은 접근 방식을 구현해야 합니다. 이러한 방법을 사용하면 전류 및 전압과 같은 변수를 쉽게 알 수 있습니다. 이 글에서 Mesh Analysis, Super mesh analysis에 대해 명확히 알려주세요.

메쉬 분석이란 무엇입니까?

메쉬는 회로 내부에 다른 루프가 없는 루프로 간주됩니다. 여기서 전체 회로 분석을 알아보기 위해 전류 대신 메쉬 전류를 변수로 사용합니다. 이 때문에 이 기법은 풀기 위해 최소한의 방정식이 필요합니다. 미지의 전류 값을 알기 위해 Kirchhoff의 전압 법칙을 사용하여 회로에서 메쉬 분석이 구현됩니다.

이것은 메쉬 전류 루프 기술이라고도 합니다. 그 후 전압 값은 옴의 법칙을 구현하여 알 수도 있습니다. 분기는 두 개의 노드를 연결하는 경로로 간주되며 회로 요소에 포함됩니다. 메쉬가 하나의 분기로만 구성된 경우 분기 전류를 메쉬 전류라고 합니다. 반면에 메쉬가 두 개의 분기로 구성된 경우 메쉬 전류는 두 메쉬 루프가 유사하거나 반대 경로에 있을 때 두 메쉬 루프의 합 또는 차이로 간주됩니다.

단계

<울>

회로의 변수를 알기 위해서는 메쉬 분석을 구현하기 위해 따라야 하는 절차가 있으며 단계는 다음과 같이 설명할 수 있습니다.

첫 번째 단계에서 메쉬를 찾아 시계 반대 방향 또는 시계 방향으로 메쉬 전류를 표시합니다.

메쉬 전류에 해당하는 각 요소에 흐르는 전류의 양을 살펴보세요.

관찰된 메쉬에 대한 모든 메쉬 방정식을 작성하십시오. 메쉬 방정식은 Kirchhoff의 법칙을 적용한 다음 옴의 법칙을 적용하여 작성됩니다.

메시 전류를 알아보려면 3단계에 따라 관찰된 메쉬 방정식을 푸십시오.

이를 통해 회로의 모든 요소에 걸친 전류 및 전압 값의 흐름은 메쉬 전류를 적용하여 알 수 있습니다.

메시 분석에서 방정식을 설정하기 위한 일반 형식

회로에서 메쉬를 식별하면 모두 하나의 방정식으로 구성됩니다. 방정식은 메쉬 전류의 전체 루프에서 전압 강하의 합계입니다. 전압과 전류 이상이 있는 회로의 경우 전압 강하는 회로의 임피던스에 특정 루프 메쉬 전류를 곱한 값으로 간주됩니다.

전압 소스가 루프 내부에 존재하는 경우 소스에 존재하는 전압은 해당 메시에 대한 전압 손실인지 또는 전압 증가인지 조건에 따라 더하거나 뺄 수 있습니다. 그러나 전류 소스가 메쉬 사이에 있지 않은 조건에서 메쉬 전류는 메쉬 전류 소스 방향에 따라 소스의 음수 또는 양수 값을 고려합니다.

메시 전류 방식

아래의 회로를 이용하면 메쉬 전류법 해석을 쉽게 알 수 있습니다. 회로에서 루프 전류 I1 및 I2는 시계 방향으로 인가됩니다.

루프 전류의 방향에 따라 전압 강하의 극성은 저항 R1, R2 및 R3에서 발생합니다. 여기서 I1 및 I2 전류는 저항 R2가 두 루프를 공유하기 때문에 반대 전류 흐름 경로를 갖습니다.

따라서 전압의 두 극성을 모두 알 수 있습니다. 실제 시나리오에서 R2는 두 단계로 분류될 수 있지만 루프 전류는 특히 분석 애플리케이션에 적용할 수 있습니다. 전압 소스의 극성이 일정하기 때문에 극성에 영향이 없습니다.

Kirchhoff의 전압 법칙을 적용하면 아래 두 방정식을 쓸 수 있습니다.

R2(I1 – I2) + R1I1 =V1 – 루프 1에서 파생됨

R2(I2 – I1) + R1I2 =-V2 – 루프 2에서 파생됨

위의 방정식에서 유사한 용어를 결합하여 배열하면 모든 방정식에서 동일한 용어가 유사한 위치에 나타납니다. 루프 전류를 알면 분기 전류를 평가할 수 있습니다. 재정렬된 방정식은 다음과 같습니다.

I1(R1 + R2) – I2R2 =V1 – For Loop 1

-I1R2 + (R2 – R3) I3 =-V2 – 루프 2의 경우

메시 분석으로 해결된 문제

이 섹션에서는 메시 전류 방법을 사용하여 회로에서 전류 찾기의 해결된 예를 보여줍니다. .

아래 회로에서 메쉬 분석 방법으로 15A 전류원을 통과하는 전압의 양을 찾으십시오. 모두 현재 소스인 경우

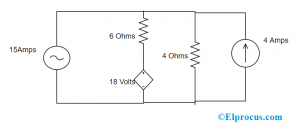
회로에 따라 병렬 저항을 사용하여 전압 소스를 전류로 변경할 가능성이 있습니다. 이를 위해 저항은 전압원과 직렬로 연결되고 저항은 전압원과 동일한 값을 가져야 하며 전압은

Vs =IsRs =4 * 4 =16V

루프의 분기 전류(I1 및 I2)를 찾고 두 루프의 전류 흐름 방향을 나타냅니다.

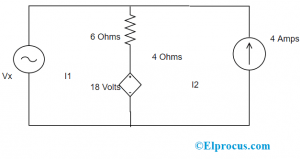
그런 다음 모든 메쉬(루프)에 대해 KVL 법칙을 적용합니다.

메쉬 – 1

Vx – (I1 – I2) – 18 =0

여기서 I1 =15

따라서 Vx + (6 * I2) =90

메쉬 – 2

18 – 6 (I2 – I1) – 4 * I2 – 16 =0

I2 =78/10

=7.8A

Mesh-1 방정식에 따름

Vx =90 – 44.4

Vx =45.6V

이것은 메시 전류 분석을 사용하여 2개의 메시 풀기의 해결된 예입니다.

여기에서 전압과 분기 전류를 찾아야 합니다. 아래 회로를 고려하십시오.

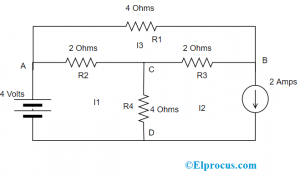
첫 번째 루프에 KVL 법칙을 적용하면 다음을 얻습니다.

V1 – R2(I1 – I3) – R4(I1 – I2) =0

4 – 2(I1) – 2(I3) – 4(I1) – 4(I2) =0

-2(I3) – 6(I1) =4

두 번째 메쉬에 KVL 법칙을 적용하면 다음을 얻습니다.

-Vc – R4(I2 – I1) – R3(I2 – I3) =0

-Vc =-4(I1) + 6(I2) – 2(I3) =0

I2 =-2A이므로

-Vc =-4(I1) -12 – 2(I3) =0

세 번째 메시에 KVL 법칙을 적용하면 다음을 얻습니다.

-R1(I3) – R3(I3 – I2) – R2(I3 – I1) =0

I2 =-2A로 대체

2(I1) – 8(I3) =0

Bu 첫 번째 및 세 번째 메쉬 방정식을 풀면 다음을 얻습니다.

I1 =4.46 및 I3 =-0.615

따라서 Vc =28.61V

그리고 분기 전류는

Iac =I1 – I3

Iac =5.075암페어

이것은 Mesh Current Analysis를 사용하여 3개의 메쉬를 해결한 해결된 예입니다.

메쉬 분석을 통해 해결한 샘플 예제입니다. 이 개념을 철저히 분석하면 복잡한 회로도 풀 수 있습니다.

수퍼 메시 분석

거대하고 복잡한 회로의 분석을 위해 슈퍼 메쉬 분석은 메쉬 분석보다 최상의 접근 방식을 제공합니다. 슈퍼 메쉬에는 공통 구성 요소를 현재 소스로 공유하는 두 개의 메쉬가 있기 때문입니다.

노드 회로 분석의 대안으로 슈퍼노드 회로 분석에 동일한 기술이 적용됩니다. 이 방법은 전압 요소를 닫고 모든 전압 소스에 대한 기준 노드 수를 최소화하여 복잡한 회로를 간소화하기 때문입니다. 슈퍼 메쉬 분석에서 현재 소스는 슈퍼 메쉬 섹션 내부에 있으므로 존재하는 모든 전류 소스에 대해 메쉬를 하나씩 최소화할 수 있습니다.

전류 소스가 회로의 허가증에 있는 경우 단일 메쉬가 고려되지 않을 수 있습니다. 반면에 KVL은 수정된 전기 회로에서 해당 메쉬에 대해서만 구현됩니다.

수퍼 메시 분석의 예를 살펴보겠습니다. 더 나은 이해를 위해.

슈퍼 메쉬 분석을 이용하여 아래 회로에 대한 V3, i1, i2, i3의 값을 찾으십니까?

Mesh-1에 KVL을 적용하면 다음을 얻습니다.

10i1 + 80(i1 – i2) + 30 (i1 – i3) =80

우리는 60i1 – 20i2 – 30i3 =80을 얻습니다.

메쉬 2 및 메쉬 3에 슈퍼 메쉬 기술을 적용하면 다음을 얻습니다.

30 =40i3+ 30 (i3 – i1) + 20(i2 – i1)

70i3 – 50i1+ 20i2 =30

슈퍼 메쉬에 있는 개별 전류 소스는 다음과 같은 예상 메쉬 전류에 해당합니다.

15ix =i3 – i2

I3 =15ix + i2

위의 세 방정식을 모두 풀면

i1 =0.58A, i2 =-6.16A 및 i3 =2.6A

V3를 찾으려면 v3 =i3 * R3이므로

V3 =2.6 * 40 =104V

메시 분석 사용

메쉬 분석의 가장 중요한 용도는 평면 회로를 분석하여 단순 전기 회로와 복잡한 전기 회로의 모든 위치에서 현재 값을 아는 것입니다.

다른 용도는 방정식을 풀기 위한 일반 계산이 어렵고 더 많은 수학 공식이 필요한 반면 메쉬 분석을 통해 적은 계산으로 충분하다는 것입니다.

메쉬 전류 분석의 다른 용도는 불균형 밀석 다리입니다. 이를 알기 위해 아래 예를 고려하십시오.

저항 R1/R4와 R2/R5의 비율이 같지 않기 때문에 R3에 어느 정도의 전압과 전류가 흐를 것임을 이해할 수 있습니다. 이러한 유형의 회로를 해결하는 것은 일반적인 직렬 병렬 기술의 접근 방식으로 복잡하다는 것을 알고 있으므로 이를 해결하기 위한 다른 접근 방식이 필요합니다.

따라서 이와 관련하여 분기 전류 방법을 적용할 수 있지만 이 방법은 Ia에서 If까지 6개의 전류가 필요하므로 여러 방정식에서 작업할 수 있습니다. 따라서 이러한 복잡성은 몇 가지 변수만 필요로 하는 Mesh 전류 방식을 통해 쉽게 줄일 수 있습니다.