양자화 잡음의 전력 스펙트럼이란 무엇입니까?

양자화 잡음에 대한 시리즈는 저자가 양자화 잡음에 대한 조사 범위를 결정하는 데 사용한 프레임워크에 대한 설명으로 시작합니다.

이 시리즈는 이전 두 시리즈에서 수행된 작업의 연속입니다. 첫 번째는 동위상 및 직교(I/Q) 조합 및 분리가 아날로그 또는 디지털 방식으로 수행되어야 하는지 여부를 조사했습니다. I/Q 변조기 및 복조기, ADC(아날로그-디지털 변환기) 및 DAC(디지털-아날로그 변환기)의 성능을 조사했습니다. 또한 이러한 맥락에서 통신 링크의 성능이 좋은 이유에 대해서도 논의했습니다.

ADC와 DAC를 데이터 변환기라고 합니다. 최신 통신 파형에 대한 ADC 및 DAC의 성능 요구 사항에 대한 정보가 많지 않기 때문에 작성자는 이러한 문제를 조사하기로 결정했습니다. ADC 및 DAC의 적절한 모델링은 ENOB(유효 비트 수) 및 ENOB와 상호 변조 다항식을 사용하는 모델에 대한 논의를 포함하여 두 번째 시리즈에서 논의되었습니다. 또한 저역 통과 필터를 포함하는 훨씬 더 효과적인 모델에 대한 저자의 제안도 검토했습니다.

시리즈 목표

데이터 변환기의 성능을 조사할 때 종종 그림 1과 같은 상황이 나타납니다.

그림 1. 데이터 변환기 사용의 단순화된 블록 다이어그램

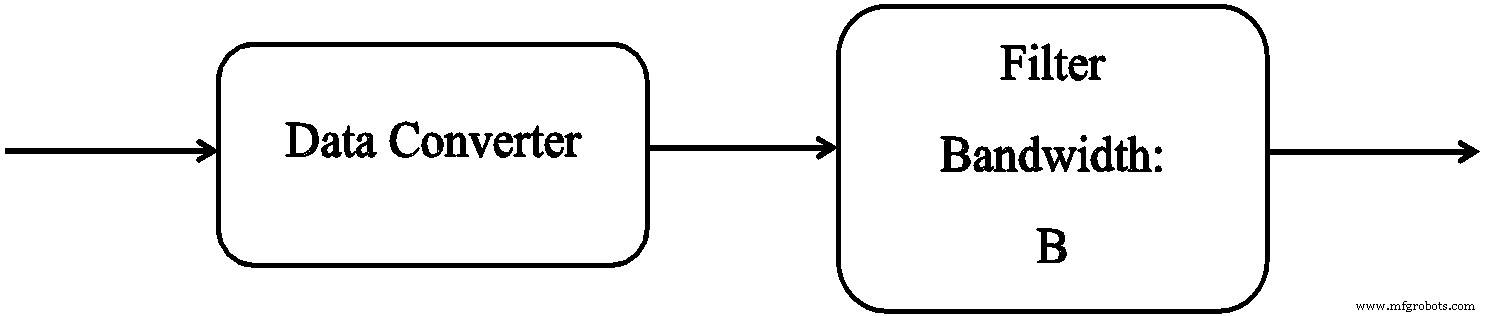
전체 노이즈는 Nyquist 대역폭(B_N )은 N입니다. 필터는 대역폭이 B_o인 대역통과 또는 저역통과일 수 있습니다. . 일반적으로 필터의 잡음 전력은 다음과 같다고 가정합니다.

필터의 소음 전력 =N(B_o / B_N )

방정식 1. 이 방정식은 모든 중심 주파수에서 ADC를 따를 수 있는 합리적인 필터에 대해 대략적으로 적용됩니다. "합리적인 필터"는 너무 좁지 않은 필터입니다.

방정식 1은 노이즈가 백색이거나 주파수에 균일하다고 가정합니다.

당신의 저자는 궁금해했습니다. 의사 양자화 잡음[14] 가정이라고도 하는 이 가정은 어떤 조건에서 참입니까?

참조 [3]에서 [32]는 이 질문의 다양한 측면을 다룹니다. 명확하게 하기 위해 작성자는 다양한 입력을 사용하여 데이터 변환기에 대한 시뮬레이션도 수행했습니다. 결과는 이 시리즈에 보고됩니다.

그는 고속 데이터 변환기에서 일반적으로 사용되는 균일 양자화(모든 단계 크기가 동일함)만을 고려했습니다. 또한 시그마-델타 변환기는 고려되지 않았습니다.

ADC 애플리케이션의 경우 RF 체인 이득이 충분히 크게 만들어지기 때문에 이전 부품의 잡음이 양자화 잡음보다 3~5dB 높기 때문에 양자화 잡음 스펙트럼은 문제가 되지 않는다. 그러나 이는 더 많은 RF 이득과 ADC의 더 높은 동적 범위를 요구하여 시스템 비용을 추가할 수 있습니다.

DAC 애플리케이션의 경우 DAC의 노이즈가 지배적이며 전송된 노이즈 스펙트럼이 흰색임을 확인하기 위해 나중에 체인에 노이즈를 추가하는 것을 원하지 않습니다.

피크, 평균 및 rms 값

입력 신호의 레벨을 정의하는 것이 중요합니다. 그림 2는 5비트로 양자화된 사인파를 보여줍니다. 이 신호의 레벨은 일반적으로 0dBFS라고 합니다. 여기서 FS는 양자화기의 전체 스케일을 나타냅니다. 그러나 RF 엔지니어는 일반적으로 rms 수량을 처리합니다. 사인파의 rms 값은 피크 값보다 3dB 낮기 때문에 그림 2의 사인파는 -3dBrmsFS 또는 0dBpeakFS입니다.

그림 2.

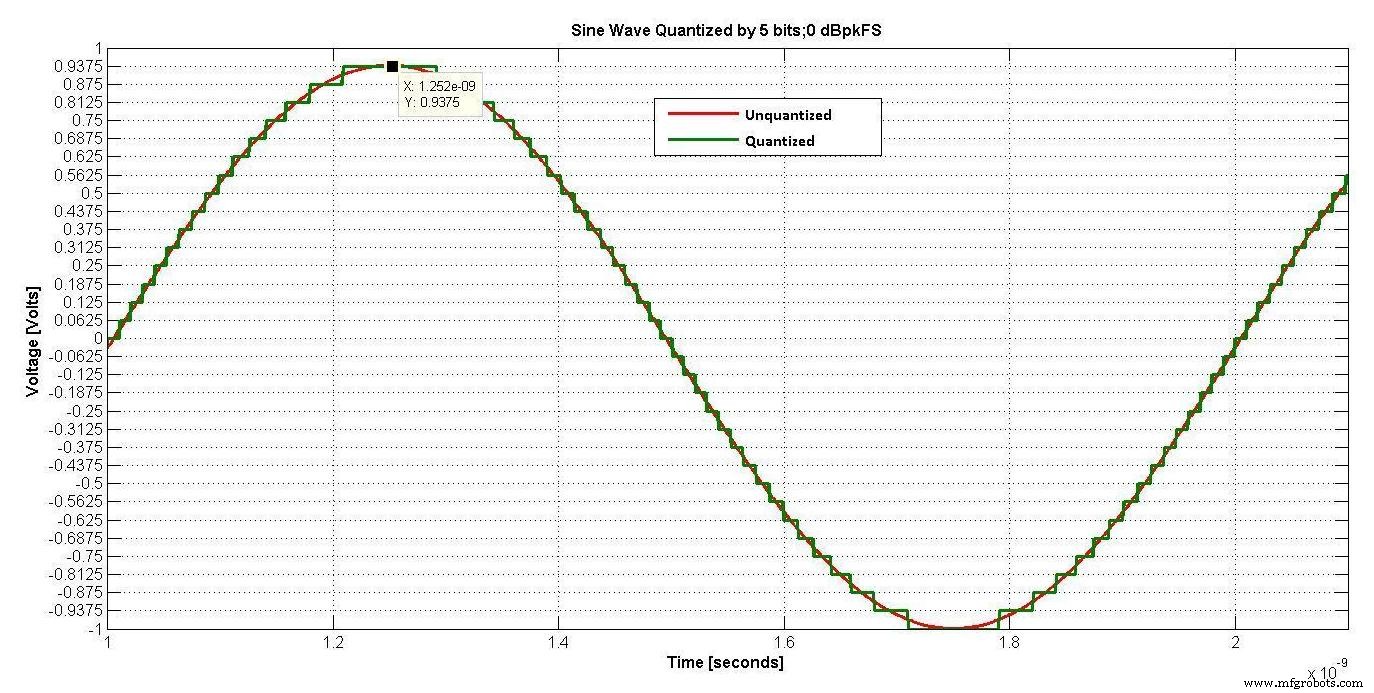
이 시리즈의 나머지 부분에서 신호 레벨은 dBrmsFS 또는 dBpeakFS로 지정됩니다.

전력은 전압의 제곱이므로 이 일정한 엔벨로프 사인파의 PAPR(Peak-to-Average Power Ratio)은 3dB입니다. 실제로 MSK와 같은 모든 대역통과 위상 또는 주파수 변조 일정 포락선 신호의 PAPR은 3dB입니다.

"잠깐 기다려요!" 친애하는 독자님. “MSK와 같은 일정한 엔벨로프 신호의 PAPR은 0dB 아닌가요? 사람들이 그렇게 부릅니다.”

사실 사람들이 이런 식으로 PAPR을 언급할 때, 그들은 봉투의 피크 전력과 봉투의 평균 전력의 비율을 말하는 것입니다. 특히 PAPR에 대한 이 참조는 신호의 복잡한 엔벨로프[33]를 특성화할 때 사용됩니다. 우리는 이 시리즈의 실제 전압과 관련되어 있으므로 PAPR은 실제 피크의 전력을 실제 평균의 전력으로 나눈 값입니다. 이 PAPR은 일반적으로 인용된 것보다 3dB 높습니다.

<시간 />

다음 기사에서는 ADC(아날로그-디지털 변환기) 출력의 스펙트럼에 대해 설명합니다.

사용된 약어

나머지 시리즈에 대해서는 다음 표를 사용하십시오.

참조

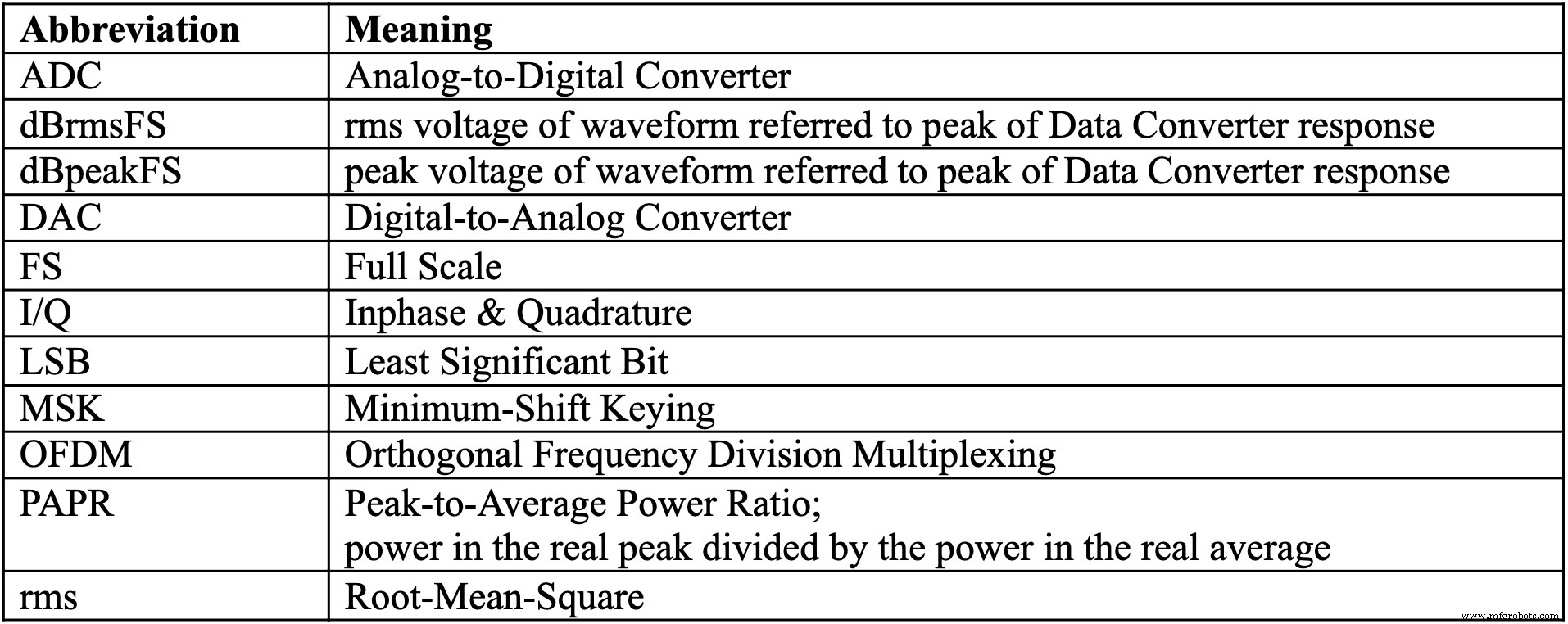
다음 참조는 시리즈의 나머지 부분에서도 사용됩니다.

소개 및 동기 부여

[1] 디지털 또는 아날로그? I와 Q의 결합과 분리는 어떻게 해야 하나요?

우수한 통신 링크 성능을 위한 요구 사항:IQ 변조 및 복조

[2] 시스템 시뮬레이션을 위해 데이터 변환기를 어떻게 모델링해야 합니까?

유효 비트 수(ENOB)를 사용한 ADC 모델링

상호변조 다항식 및 유효 비트 수를 사용하여 ADC 모델링

ADC 모델 및 DAC 모델링에 저역 통과 필터 추가

클리핑 효과가 있거나 없는 양자화 노이즈

ADC 및 DAC

[3] 말로베르티, 프랑코; 데이터 변환기; 스프링거 퍼블리싱; 2007

클리핑 효과가 있거나 없는 ADC 전용

[4] 레버, K. V.; Cattermol, K.W., "소음 스펙트럼 양자화," Electrical Engineers, Proceedings of the Institution of, vol.121, no.9, pp.945,954, 1974년 9월

레버, K.V.; Cattermole, K.W., "정오표:노이즈 스펙트럼 양자화," Electrical Engineers, Proceedings of the Institution of, vol.122, no.3, pp.272, 1975년 3월

[5] Gersho, A, "양자화의 원리", Circuits and Systems, IEEE Transactions on, vol.25, no.7, pp.427, 436, 1978년 7월

[6] Gersho, A, "양자화", Communications Society Magazine, IEEE, vol.15, no.5, pp.16, 16, 1977년 9월

[7] Schuchman, L., "디더 신호와 양자화 잡음에 미치는 영향", Communication Technology, IEEE Transactions on, vol.12, no.4, pp.162, 165, 1964년 12월

[8] Walden, R.H., "아날로그-디지털 변환기 및 관련 IC 기술", 화합물 반도체 집적 회로 심포지엄, 2008. CSIC '08. IEEE, vol., no., pp.1, 2, 2008년 10월 12-15일

[9] Walden, R.H., "아날로그-디지털 변환기에 대한 성능 동향," Communications Magazine, IEEE, vol.37, no.2, pp.96, 101, 1999년 2월

[10] Walden, RH, "아날로그-디지털 컨버터 기술 비교," 갈륨 비소 집적 회로(GaAs IC) 심포지엄, 1994, Technical Digest 1994., 16th Annual, vol., no., pp.217,219, 16- 1994년 10월 19일

[11] Walden, R.H., "아날로그-디지털 변환기 조사 및 분석," 통신 분야의 선택 영역, IEEE Journal on, vol.17, no.4, pp.539, 550, 1999년 4월

[12] Morgan, DR, "A/D 변환에 대한 응용 프로그램이 있는 대역 제한 가우스 랜덤 프로세스에 대한 유한 제한 효과", 음향, 음성 및 신호 처리, IEEE 트랜잭션 on, vol.36, no.7, pp.1011 ,1016, 1988년 7월

[13] Chow, P.E.-K., "파형 양자화 성능," Communications, IEEE Transactions on, vol.40, no.11, pp.1737, 1745, 1992년 11월

[14] Dardari, D., "고속 WLAN 수신기에서 조인트 클리핑 및 양자화 효과의 정확한 분석" Communications, 2003. ICC '03. IEEE International Conference on, vol.5, no., pp.3487, 3492 vol.5, 2003년 5월 11-15일

[15] Gray, R.M., "Quantization noise spectra", Information Theory, IEEE Transactions on, vol.36, no.6, pp.1220,1244, 1990년 11월

[16] Echard, J.; Watt, M.L., "컬러 노이즈에서 사인파의 양자화 노이즈 스펙트럼", Signal Processing, IEEE Transactions on, vol.39, no.8, pp.1780,1787, 1991년 8월

[17] 허징; 리강; 쉬시빈; Yao Yan, "선형 디지털 필터의 양자화 잡음 스펙트럼 추정" Communication Technology Proceedings, 2000. WCC - ICCT 2000. International Conference on, vol.1, no., pp.184, 187 vol.1, 2000

[18] Bennett, W.R., "양자화된 신호의 스펙트럼", Bell System Technical Journal, The, vol.27, no.3, pp.446, 472, 1948년 7월

[19] Mohamed, EM, "MIMO-Constant Envelope Modulation을 위한 낮은 복잡도 채널 추정 기법," Wireless Technology and Applications(ISWTA), 2013 IEEE Symposium on, vol., no., pp.97, 102, 22-25 Sept . 2013

[20] Clavier, A G.; Panter, P.F.; Grieg, D.D., "펄스 카운트 변조 시스템의 왜곡", American Institute of Electrical Engineers, Transactions of the, vol.66, no.1, pp.989, 1005, 1947년 1월

클리핑 효과가 있거나 없는 DAC 전용

[21] Ling, W.A, "Shaping Quantization Noise and Clipping Distortion in Direct-Detection Discrete Multitone," Lightwave Technology, Journal of, vol.32, no.9, pp.1750, 1758, 2014년 5월 1일

클리핑 효과만; ADC 전용

[22] Mazo, JE, "클리핑, DC 바이어스, 가우스 노이즈[광 통신]의 점근적 왜곡 스펙트럼", Communications, IEEE Transactions on, vol.40, no.8, pp.1339, 1344, 1992년 8월

[23] Dakhli, M.C.; Zayani, R.; Bouallegue, R., "레일리 페이딩 채널에서 MIMO OFDM 시스템의 다항식 모델을 사용한 성능 분석 및 비선형 왜곡 효과의 이론적 특성화 및 보상" 컴퓨터 및 통신(ISCC), 2013 IEEE Symposium on, vol., no., pp .000583,000587, 2013년 7월 7-10일

[24] Dardari, D.; Tralli, V.; Vaccari, A, "OFDM 시스템에서 비선형 왜곡 효과의 이론적 특성화", Communications, IEEE Transactions on, vol.48, no.10, pp.1755, 1764, 2000년 10월

[25] Giannetti, F.; 로티치, V.; Stupia, I, "MC-CDMA 전송에서 비선형 왜곡 잡음의 이론적 특성화", 개인, 실내 및 모바일 무선 통신, 2006 IEEE 17차 국제 심포지엄, vol., no., pp.1,5, 11-14 Sept. 2006년

[26] Van Vleck, J.H.; Middleton, D., "잘린 노이즈의 스펙트럼", IEEE Proceedings, vol.54, no.1, pp.2, 19, 1966년 1월

기타 관련 수학적 처리

뉴욕주 에르몰로바; Haggman, S.-G., "복소수 신호에 대한 Bussgang 이론의 확장", 신호 처리 심포지엄, 2004년, NORSIG 2004년. 제6회 Nordic의 회보, vol., no., pp.45, 48, 11- 2004년 6월 11일

[28] Requicha, Aristides AG, "양자화된 랜덤 변수의 함수 기대값", 통신, IEEE 트랜잭션 on, vol.21, no.7, pp.850,854, 1973년 7월

[29] Pirskanen, J.; Renfors, M., "다중 모드 이동 단말기의 양자화 및 지터 요구 사항" Communications, 2001. ICC 2001, IEEE International Conference on, vol.4, no., pp.1182, 1186 vol.4, 2001

Irons, Fred H.; 라일리, K.J.; Hummels, D.M.; Friel, G.A, "노이즈 전력 비율 이론 및 ADC 테스트", 계측 및 측정, IEEE Transactions on, vol.49, no.3, pp.659,665, 2000년 6월

[31] Widrow, B., "Nyquist Sampling Theory에 의한 거친 진폭 양자화 연구" Circuit Theory, IRE Transactions on, vol.3, no.4, pp.266, 276, 1956년 12월

[32] Rowe, H.E., "가우스 입력을 사용한 메모리 없는 비선형성:기본 결과," Bell System Technical Journal, The, vol.61, no.7, pp.1519, 1525, 1982년 9월

[33] VanTrees, 해리 L; 탐지, 추정 및 변조 이론, III부, 레이더/소나 신호 처리 및 잡음의 가우스 신호; 존 와일리와 선즈; 1971. 부록:"대역 통과 신호, 시스템 및 프로세스의 복잡한 표현" AES-1, 발행:6, 1979, 페이지:840 – 848.