나노링 기반 플라즈모닉 렌즈의 편광 의존 준원거리 초초점화 전략

방법

이 연구에서 조사된 NRPL은 나노슬릿 기반 PL에 널리 적용되는 파면 재구성 이론을 사용하여 설계되었습니다[11, 15]. 원하는 위치에 초점을 맞추기 위해 빛이 i를 통과할 때 발생하는 상대적 위상 지연 -th 개별 나노링은 기하학적 광학을 기반으로 다음 조건을 충족해야 합니다.

여기서 −Δϕ (r _나 )는 내부 중심의 첫 번째 나노링과 i 사이의 상대적 위상차입니다. -th 나노링, r 반경, λ ₀ 입사광의 자유 공간 파장, n 임의의 정수이고 f ₀ 는 설계된 초점 거리입니다.

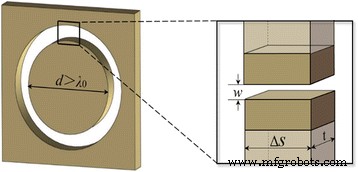
조사된 NRPL의 기본 구성 요소는 금속 필름에 패턴화된 나노링입니다. Ref.에 따르면 [29], 직경이 입사광의 파장보다 클 때 금속 벽으로 둘러싸인 공기 나노링은 그림 1의 삽입도와 같이 MIM 도파관 모델에 근사할 수 있습니다. 위상 지연은 주로 실수 부분에 의해 정의됩니다. 전파 상수 β의 , Re(β로 표현됨 )•t , 여기서 t 나노링의 두께입니다. 분산 관계에 따라 복소 전파 상수 β 다음과 같이 계산할 수 있습니다.

금 필름에 내장된 개별 나노링의 MIM 도파관 모델. 삽입 나노링의 임의의 작은 부분을 확대하여 보여줍니다.

여기서 k ₀ 진공에서 파동 벡터를 나타내고 ε _d 그리고 ε _m 는 각각 유전체와 금속의 유전율입니다. 식에 기초 (2) 전파 상수 β 나노링의 너비에 따라 다릅니다. 따라서 주어진 두께 t를 가진 평면 렌즈의 경우 , 발생된 위상 지연은 단순히 너비 w에 의해 결정됩니다. 빛이 통과할 때 개별 나노링의 우리 연구에서 유전체는 유전율이 ε인 공기로 설정됩니다. _d =1, 두께가 t인 금막 400 nm의 입사 파장에서 유전율이 ε인 650 nm가 사용됩니다. _m =−12.8915 + 1.2044i [15]. 또한, 우리가 이전에 보고한 바와 같이 [16], 인접한 두 MIM 도파관에서 전파하는 빛의 결합 효과는 위상 지연에 중요한 역할을 합니다. 특히 간격 금속 벽이 표피 깊이 δ의 두 배보다 작을 때 _m , [30]으로 추정할 수 있습니다.

따라서 계산된 피부 깊이 δ _m 약 28nm입니다. 커플링 효과를 고려하여 0.38 λ 슈퍼포커싱 능력을 가진 나노슬릿 기반 PL ₀ 해결 방법은 이전 연구에서 보고되었습니다[16]. 여기서, 편광 상태(SOP)가 집속 성능에 미치는 영향을 뚜렷하게 분석하기 위해 인접한 두 나노링 사이의 간격 벽은 2δ보다 훨씬 큰 100nm로 설계되었습니다. _m 커플링 효과를 제거합니다.

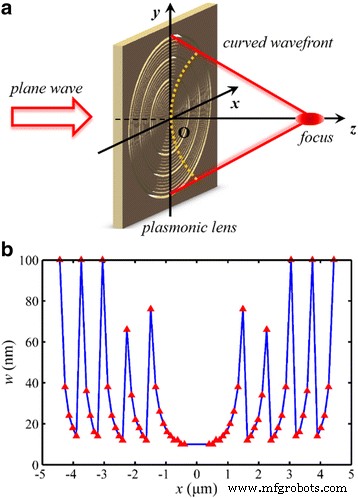
설계된 NRPL의 개략도는 그림 2와 같으며 웨이브프론트를 재구성하기 위해 총 32개의 동심 나노링이 포함되어 있습니다. 원하는 위상 변조를 위한 나노링의 너비는 10~100nm입니다. 목표 초점 거리 f ₀ 1300 nm(2 λ) ₀ ). MIM 도파관 모델을 효율적으로 활용하기 위해 가장 안쪽에 있는 나노링의 최소 직경을 800nm로 설정했습니다. 게다가, 우리의 이전 연구[15]에서 논의된 초점 이동을 피하기 위해 총 위상 차이는 0.96의 예측 개구수(NA)로 10π만큼 큽니다. 결과적으로 이론적인 Rayleigh 회절 한계는 0.61 λ로 계산됩니다. ₀ /NA [31], 413 nm(~0.64 λ ₀ ).

NRPL의 개략도. 아 입사광은 일반적으로 렌즈를 비춥니다. ㄴ 렌즈의 구조적 매개변수. 빨간색 삼각형의 좌표값 반지름 r을 나타냅니다. 및 너비 w 해당 나노링의

공간 강도 분포, 특히 포커싱 성능에 대한 입사광의 SOP 영향을 조사하기 위해 설계된 NRPL을 선형, 원형, 방위각 및 방사형 편광으로 각각 조명했습니다. 모든 경우는 FDTD 수치 시뮬레이션에 의해 계산되었습니다. 매트릭스 광학에 따르면 다양한 편광을 Jones 매트릭스 형식으로 설명할 수 있으며 해당 매트릭스 표현을 적용하여 입사광을 정의합니다. 모델의 경계는 레이어 번호가 12인 완벽하게 일치하는 레이어(PML)였습니다. 시뮬레이션에서 계산 정확도와 메모리 소비의 균형을 맞추기 위해 메쉬 크기는 출력 영역에서 10nm, 주변에서 5nm로 설정되었습니다. 초점 영역.

결과

I 선형 편광

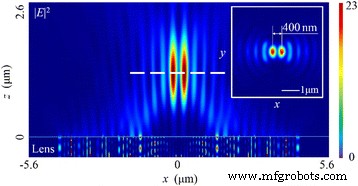
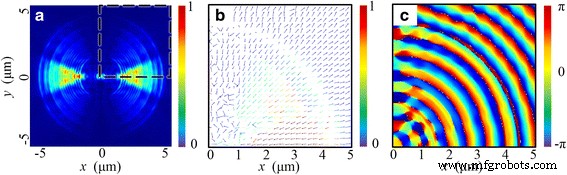
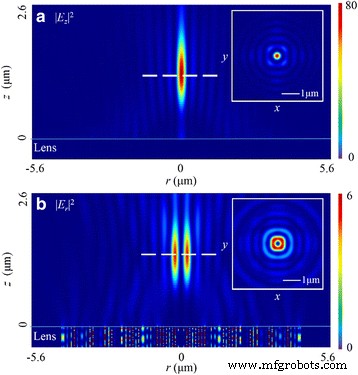
선형편광의 경우 SOP는 공간적으로 균일하며 이 경우 전기벡터의 방향은 x 중심선. 빛이 NRPL을 비추면 총 전계에서 서로 400nm 떨어진 곳에 두 개의 초점이 존재합니다 |E | ² 그림 3에 나와 있습니다. 둘 다 반치폭(FWHM)이 210nm(~0.32 λ)이지만 ₀ ) 초점면에서 시뮬레이션 결과는 z에 정확히 원형 초점이 있어야 하는 파면 재구성 이론에 기반한 설계와 강도 분포가 명백히 다르다는 것을 나타냅니다. 축(광축이라고도 함).

총 전기장의 세기 분포 패턴 |E | ² 선형 편광 입사광의 경우. 삽입 초점면의 강도 패턴을 보여줍니다. 초점 거리는 1215nm(편차 6.54%)입니다. 두 초점의 FWHM은 ~0.32 λ입니다. ₀ , 서로 400nm 떨어져 있고 초점 심도(DOF)는 ~1.68 λ입니다. ₀

시뮬레이션과 이론적인 설계의 차이점을 분석하기 위해 전기장 성분의 강도 분포를 조사했습니다. Fig. 4와 같이 x-에 타원형의 초점과 FWHM이 나타난다. 그리고 y- 방향은 220 nm(~0.34 λ ₀ ) 및 457nm(~0.70 λ ₀ ), 각각. 이 패턴은 Ref.의 실험 결과와 잘 일치합니다. 동일한 편광이 적용된 곳 [18]. 그러나 시뮬레이션은 |E의 분포 패턴이 | ² 세로 구성 요소의 패턴과 유사합니다 |E _z | ² 전체 전기 에너지의 79.8%를 차지합니다. 따라서 차이는 주로 |E의 비정상 분포에 기인합니다. _z | ² .

가로 성분의 강도 분포 |E _r | ² 초점 평면에서. 삽입 타원형 모양의 초점을 보여줍니다. 초점 거리는 1425nm(편차 9.62%)입니다. |이 _r | ² 전체 전기 에너지의 20.2%를 차지합니다. DOF는 ~1.41 λ입니다. ₀

이러한 현상은 궁극적으로 NRPL의 전송 특성으로 설명할 수 있다. 한편, 금속과 유전체의 계면에서 SPP의 여기(excitation)는 일반적으로 입사광의 국부적 편광 방향에 의존합니다. 횡전기(TE) 파동은 여기에 기여할 수 없습니다. 반면에 MIM 도파관의 subwavelength 구조로 인해 SP파만 이 렌즈를 통해 전파될 수 있습니다[32]. 렌즈의 회전 대칭으로 국부 횡자기(TM) 성분은 방위각 θ에 따라 변합니다. 코사인 형태로. 따라서 그림 5a와 같이 |E의 세기분포는 | ² 렌즈의 끝면 바로 위에 있는 , y =0 영역(−π/4 <θ <π/4). 이에 따라, Poynting 벡터는 그림 5b에 표시된 것처럼 끝면의 반경 방향을 따라 전파됩니다. 따라서 E의 벡터 방향은 기본적으로 E의 주요 내용을 형성하는 광축과 평행합니다. _z . 대칭 보강 간섭으로 인해 원형 초점 대신 초점 평면에 두 개의 초점이 나타납니다.

단면의 전기장 분포 특성은 렌즈의 끝 표면에서 불과 50nm 위입니다. 아 |E의 정규화된 강도 분포 | ² . ㄴ 점선 내의 포인팅 벡터 분포 지역 a. ㄷ E의 해당 위상 분포 _z

II 원형 편광

원형편광의 상태가 시간에 따라 주기적으로 변하기 때문에 시뮬레이션된 결과는 시간 평균 필드 분포입니다. 이 편광된 빛으로 렌즈를 비추면 |E에 도넛 모양의 초점이 형성됩니다. _z | ² . 그림 6a에서 볼 수 있듯이 이 필드의 초점 거리는 1185 nm로 설계 값에 대해 8.85% 편차를 보여줍니다. 도넛의 너비는 210nm(~0.32 λ ₀ ), 반경은 400 nm입니다. 초점 심도(DOF)는 ~1.65 λ입니다. ₀ . |E의 무게 _z | ² 전체 전기에너지의 80.6%를 차지한다. 또한 |E에서 _r | ² , 공간 영역의 중첩은 1405nm 초점 거리(편차 8.08%)로 원형 초점을 생성합니다. FWHM은 295nm(~0.45 λ ₀ ) 이 필드에서 DOF는 ~1.68 λ입니다. ₀ . 또한 r-z의 두 분포 패턴 평면은 x와 유사합니다. -z 선형 편광 입사광의 경우 평면. 방사형 전기장 성분을 고려하여 FWHM을 222nm(~0.34 λ ₀ ).

|E의 강도 분포 패턴 _z | ² 그리고 |E _r | ² r-z 원형 편광의 경우 평면. 아 |E에서 _z | ² , FWHM, DOF 및 초점 거리는 ~0.32 λ ₀ , ~1.65 λ ₀ , 및 1185 nm. ㄴ |E에서 _r | ² , FWHM, DOF 및 초점 거리는 ~0.45 λ ₀ , ~1.68 λ ₀ , 각각 1405nm

III 방위각 편파

방위각으로 편광된 입사광의 경우 전기 벡터는 NRPL의 금/진공 경계면에 평행한 반경 방향에 수직입니다. 방위각으로 편광된 빛이 렌즈를 비추면 국부적 TE파가 인터페이스의 SPP를 여기시키지 못합니다. 따라서 나노링의 투과 거리는 그림 7과 같이 너비에 비례합니다. 구조와 조명이 모두 회전 대칭이기 때문에 강도 분포 패턴과 NRPL 구조의 절반만 표시됩니다. 투과광은 무시할 수 있으며 출력 영역에 뚜렷한 초점이 없습니다.

렌즈 영역의 강도 분포 패턴과 단면도. 나노링에서 SP가 아닌 파동의 전송 거리는 슬릿 폭에 비례합니다.

IV 방사형 편광

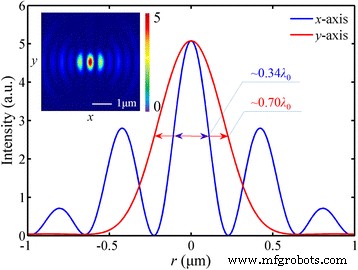
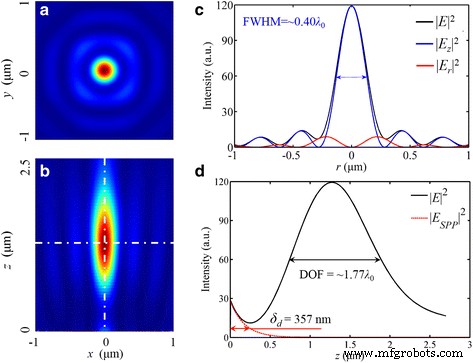
방위각으로 편광된 빛에 해당하는 방사상 편광된 빛은 국부 TM파로 간주될 수 있으며 이 편광 속성은 SPP의 여기 조건과 일치하여 초점에서 더 높은 최대 강도에 기여합니다. 총 전기장 E , 최대 강도는 선형 편광 입사광에 대한 것보다 5배 더 큽니다. 또한 276nm(~0.42 λ ₀ ) |E의 FWHM | ² 시뮬레이션된 강도 분포는 고 NA 굴절 렌즈의 포커싱 능력과 매우 유사합니다[33]. 게다가 이 포커싱 성능은 여전히 ​​|E에 의존합니다. _z | ² , 전체 전기 에너지의 82.0%를 차지합니다.

|E의 강도 분포 | ² 방사상으로 편광된 입사광의 경우. 아 , b 초점면에서의 분포와 x에서의 분포 -z 교차 구역. ㄷ 반경 방향의 강도 프로파일입니다. d 검은색 실선이 있는 광축을 따른 강도 프로파일 시뮬레이션의 총 전기장 강도 분포와 빨간색 점선 SPP의 계산된 곡선입니다. 초점 거리는 1275nm(편차 1.92%)입니다. |E의 FWHM | ² 그리고 |E _z | ² 272 nm(~0.42 λ ₀ ) 및 260nm(~0.40 λ ₀ ), 각각. DOF는 ~1.77 λ입니다. ₀

이전의 경우와 달리 |E에 원형 모양의 초점이 있습니다. _z | ² . 게다가 이 구성 요소는 |E의 분포 패턴도 결정합니다. | ² . 그림 9a에 나타난 바와 같이 |E의 FWHM _z | ² 260 nm(~0.40 λ ₀ ) 나노슬릿 기반 PL의 경우 초점 라인에 가깝습니다[16]. 특히 초점거리는 1275nm이다. 설계 값과 비교하여 상대 오차가 1.9%로 감소합니다. 그러나 초점거리는 |E에서 1455nm(편차 11.2%)입니다. _r | ² . 그림 9b에서 볼 수 있듯이 227nm 너비(~0.35 λ ₀ ) 이 분야에서. DOF는 ~1.60 λ입니다. ₀ .

|E의 강도 분포 패턴 _z | ² 그리고 |E _r | ² r-z 방사상으로 편광된 빛의 경우 평면. 아 |이 _z | ² r-z 패턴 비행기. 삽입 초점면에서 원형 모양의 초점을 보여줍니다. ㄴ 가로 |E _r | ² r-z 패턴 비행기. 삽입 초점면에서 도넛 모양의 초점을 보여줍니다.

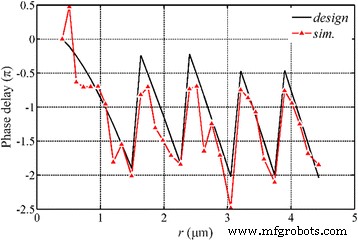
나노링에서 SP파의 위상 지연은 그림 10과 같이 조사됩니다. 시뮬레이션은 위상 변조가 NRPL의 구조적 매개변수에 의해 극적으로 영향을 받고 입사면과 출력 표면 사이의 시뮬레이션된 위상 지연이 다음과 같다는 것을 나타냅니다. 기본적으로 Eq.에 따라 계산된 값과 동일합니다. (2). 렌즈의 끝면에서 SP파는 여전히 반경 방향을 따라 전파되고 표면의 중앙에는 강도가 초점 강도의 1/5인 핫스팟이 있습니다. 회전 대칭 분포를 갖는 SP파의 보강 간섭은 전파하는 파동을 구성하고 준 원거리 필드에서 원형 초점을 구현합니다.

방사상으로 편광된 입사광에서 NRPL의 위상 분석

토론

I Superfocusing NRPL 기능

선형, 원형 ​​및 방사형 편광을 포함하여 다양한 SOP를 갖는 입사광이 적용됨에 따라 하위 회절 한계 초점을 구현할 수 있습니다. 초점 모양이 SOP의 영향을 받지만 이러한 초점의 특성 크기는 모두 레일리 회절 한계(413nm)를 극복합니다. 시뮬레이션 결과는 NRPL의 슈퍼포커싱 기능을 성공적으로 입증했으며 초점면의 강도 분포는 비회절 빔을 설명하는 데 사용되는 베셀 함수와 유사합니다.

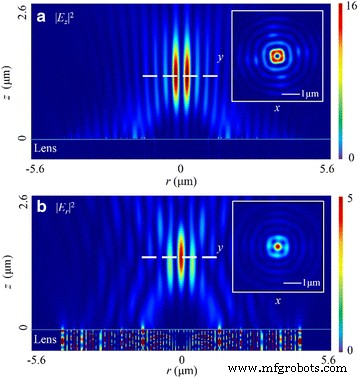
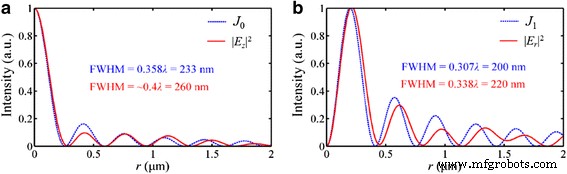
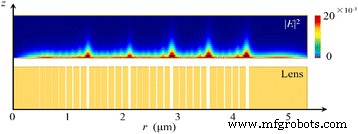
방사상으로 편광된 입사광의 경우 그림 11과 같이 |E의 강도 분포가 _z | ² 0차 베셀 함수 J와 동일합니다. ₀ (케이 _종 ⋅ n ⋅ r ), 여기서 n 그리고 r 는 각각 환경 매질의 굴절률과 광축까지의 반경 거리입니다. 초점의 FWHM은 J로 계산된 메인 로브의 크기보다 약간 큽니다. ₀ . 특히, 시뮬레이션은 비회절 빔이 준원거리 필드에서 구현될 수 있음을 나타냅니다. SP파는 소멸파의 일종으로 출구면에서 멀어질 때 기하급수적으로 감소하며, 진공에서의 전파 거리는 [30]에 의해 계산될 수 있습니다.

<사진>

방사상으로 편광된 입사광 아래의 초점면에서 NRPL의 강도 프로파일. 아 |E의 분포 _z | ² 0차 베셀 함수 J와 유사 ₀ . ㄴ |E의 분포 _r | ² 1차 베셀 함수 J와 유사 ₁

$$ {\delta}_d=\frac{1}{k_0}{\left|\frac{\mathrm{Re}\left({\varepsilon}_m\right)+{\varepsilon}_d}{{\varepsilon_d }^2}\right|}^{\frac{1}{2}} $$ (4)

여기서 ε _d 그리고 ε _m 는 각각 유전체와 금속의 유전율입니다. 따라서 δ _d 그림 8d에 표시된 시뮬레이션과 일치하는 357 nm입니다. 따라서 초점에서 SP파의 강도는 준 원거리 영역에서 무시될 수 있습니다.

II 모양의 초점

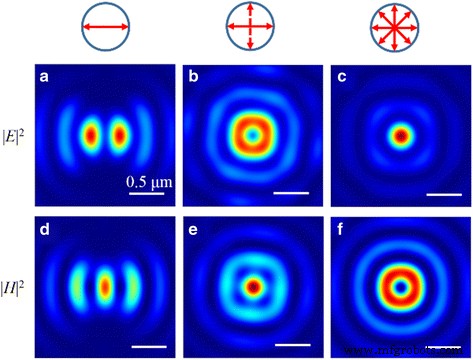
SOP를 변조하면 그림 12와 같이 초점면에서 타원형, 원형 ​​및 도넛형 초점을 구현할 수 있습니다. 이 현상은 subwavelength 초점 크기에 기인하며 원형 유형을 구현할 수 없습니다. 동시에 전기장과 자기장에 초점을 맞춥니다. 따라서 도넛형 초점은 자기장(또는 전기장)에서 구현되고 원형형 초점은 해당 전기장(또는 자기장)에서 구현됩니다. 특히 세로 자기장이 없기 때문에 |H | ² |E의 패턴과 동일합니다. _r | ² . 또한 |E _z | ² 전체 전기에너지의 약 80.0%를 차지하며 입사광의 SOP에 영향을 받지 않습니다.

<그림>

전기장의 정규화된 강도 패턴 |E | ² 및 자기장 |H | ² NRPL이 편광된 빛에 의해 조명될 때 초점면에서. 아 |이 | ² 그리고 d |안 | ² 선형 편광 입사광 분포. ㄴ |이 | ² 및 e |안 | ² 원편광 입사광 분포. ㄷ |이 | ² 및 f |안 | ² 방사상으로 편광된 입사광 분포

초점 거리의 III 변조

다른 경우에 시뮬레이션된 초점 거리는 기본적으로 원하는 위치에 가깝습니다. f ₀ (1300 nm), 표 1과 같이 _r | ² 세로 필드보다 약 200nm 더 깁니다. |E _z | ² , 입사광의 SOP와 상관없이 편차가 공통적으로 존재합니다.

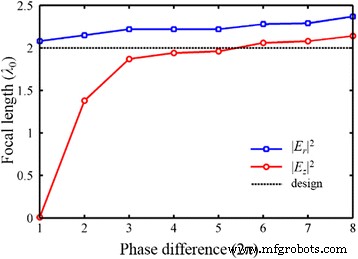
이론적으로 파면 재구성 이론은 근거리장에서 원거리장 영역까지 임의의 초점 거리로 NRPL을 설계하는 데 적합합니다. 그러나 설계된 플라즈몬 렌즈의 실제 초점 거리가 설계된 초점 거리와 잘 일치하는지 여부는 렌즈의 전체 위상차에 따라 다릅니다. 편차는 진폭형 초점과 위상형 초점의 구별에 기인할 수 있습니다[34]. MIM 도파관의 위상 변조는 방사형 성분을 목표로 하기 때문에 |E의 초점 거리는 _r | ² 최소 2π의 총 위상차가 만족될 때 파면 재구성 이론에 의해 변조될 수 있습니다[15]. 종방향 성분의 경우 총 위상차(>10π)가 클수록 일관성에 유리합니다. 그림 13과 같이 위상차가 2π에서 16π로 증가할 때, 이에 상응하는 NA 0.75에서 0.96, 진폭형 초점은 |E _z | ² 렌즈의 출력면에서 원하는 위치로 이동합니다. |E의 강도 분포로 | ² |E에 의해 결정됩니다. _z | ² , NA는 전체 전기장의 초점 거리에 극적으로 영향을 줄 수 있습니다. 그러나 |E에서 초점 거리의 변화는 _z | ² 전체 위상차의 증가와 함께 점진적으로 감소합니다. 한편, 위상형 포커스의 위치는 |E _r | ² 비교적 안정적이다. NA가 높은 NRPL이 적용될 때 |E의 강도 분포를 기반으로 파생된 초점 거리의 편차가 여전히 있습니다. _x | ² 그리고 |E _z | ² , 편차는 거의 변하지 않습니다. 따라서 NRPL의 초점 거리는 위상 변조 및 구조 최적화로 효과적으로 제어할 수 있지만 가로 및 세로 구성 요소 필드에서는 동일한 초점 거리를 얻을 수 없습니다.

<사진>

총 위상차가 2π에서 16π로 증가하는 NRPL의 초점 거리

비동축 상황에서 IV 집중 성능

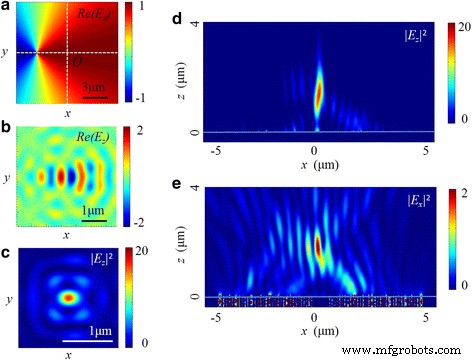
The non-coaxial situation is a common problem in the experiment, and its effect on the focusing performance should be considered. As shown in Fig. 14, the center of the radially polarized light deviates 3 μm from the optical axis of the NRPL along the x axis. Compared with Figs. 8 and 9, the intensity distributions both in x-z cross section and in focal plane are apparently changed. In the longitudinal electric field, an elliptical focus is located at 1340 nm away from the exit surface of the lens. The FWHMs in x-z and y-z planes are 0.51 and 0.38 λ ₀ , 각각. On the other hand, the distribution in transverse field is also distorted, where the intensity of one side lobe is higher than the other one. Furthermore, compared with the coaxial condition, the decrease of the maximum intensity in the total electric field is more than 85%.

The intensity distribution of the NRPL in the non-coaxial situation. 아 The real part of E _x of radially polarized incident light. ㄴ , ㄷ The distribution of Re(E _z ) and |E _z | ² in the focal plane. d , e The distribution of |E _z | ² and |E _x | ² in the x-z plane

The preliminary simulation indicates that the non-coaxial situation indeed influences the intensity distribution and the desired focusing performance of lens. Therefore, it is essential to guarantee the coaxiality between the incident light and the lens center during the experiment.

Conclusions

In summary, we build a NRPL with a high NA utilizing the wavefront reconstruction theory and the dispersion relation of the MIM waveguide. We also investigate the polarization-dependent focusing performance in the quasi-far field, including the focal length, FWHM, DOF, and the maximum intensity. The conventional polarized light, such as the linearly, circularly, radially, and azimuthally polarized light, are all considered. The simulations demonstrate the superfocusing capability of the designed NRPL. Utilizing the polarization-dependent property, the sub-diffraction-limit elliptical-, circular-, and donut-shape foci can be realized. However, one limitation of this work is that the proposed design strategy to realize the superfocusing performance of NRPLs is aimed for the quasi-far-field region, although to the best of our knowledge, the similar focusing capability in this region is rarely reported. In addition, we discover the underlying physical phenomenon on the focal shift and propose a more effective way to control the focusing position by employing both the transverse and longitudinal fields. There are considerable engineering applications for the nanoring-based superfocusing lenses, ranging from the super-resolution imaging, particle acceleration, quantum optical information processing to the optical data storage.

약어

DOF:

Depth of focus

FDTD:

Finite-difference time-domain

FWHM:

Full-width at half maximum

MIM:

Metal-insulator-metal

NRPL:

Nanoring-based plasmonic lenses

PML:

Perfectly matched layer

SOP:

State of polarization

SPPs:

Surface plasmon polaritons

TE:

Transverse electric

TM:

Transverse magnetic

슈퍼커패시터 애플리케이션을 위한 그래핀 및 고분자 복합 재료:검토 금속 보조 화학 식각 중 다공성 실리콘 나노와이어의 형태적 진화 및 식각 역학 풀기