MATLAB - 미적분학

MATLAB은 미분 및 적분 미적분 문제를 풀고 모든 차수의 미분 방정식을 풀고 극한을 계산하는 다양한 방법을 제공합니다. 무엇보다 복잡한 함수의 그래프를 쉽게 플로팅할 수 있고 원래의 함수와 그 도함수를 풀면 그래프에서 최대값, 최소값 및 기타 고정점을 확인할 수 있습니다.

이 장에서는 미적분 문제를 다룰 것입니다. 이 장에서는 함수의 극한을 계산하고 극한의 속성을 확인하는 미적분학 전 개념에 대해 설명합니다.

다음 장에서 Differential , 우리는 표현식의 도함수를 계산하고 그래프에서 국소 최대값과 최소값을 찾습니다. 또한 미분 방정식 풀이에 대해서도 논의할 것입니다.

마지막으로 통합 챕터에서는 적분 미적분에 대해 논의할 것입니다.

한도 계산

MATLAB은 제한을 제공합니다. 한계를 계산하는 기능. 가장 기본적인 형태의 한도 함수는 식을 인수로 취하고 독립 변수가 0이 될 때 식의 극한을 찾습니다.

예를 들어, 함수 f(x) =(x ³ + 5)/(x ⁴ + 7), x가 0이 되는 경향이 있기 때문입니다.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB은 위의 명령문을 실행하고 다음 결과를 반환합니다 -

ans =
   5/7

제한 기능은 기호 컴퓨팅 영역에 속합니다. 기호를 사용해야 합니다. 어떤 기호 변수를 사용하고 있는지 MATLAB에 알려주는 함수입니다. 변수가 0이 아닌 다른 숫자로 가는 경향이 있으므로 함수의 한계를 계산할 수도 있습니다. lim _x->a를 계산하려면 (f(x)), 인수와 함께 limit 명령을 사용합니다. 첫 번째는 표현식이고 두 번째는 숫자입니다. x 접근 방식, 여기 a입니다. .

예를 들어, 함수 f(x) =(x-3)/(x-1)의 극한을 계산해 봅시다. x는 1이 되는 경향이 있기 때문입니다.

limit((x - 3)/(x-1),1)

MATLAB은 위의 명령문을 실행하고 다음 결과를 반환합니다 -

ans =
   NaN

다른 예를 들어 보겠습니다.

limit(x^2 + 5, 3)

MATLAB은 위의 명령문을 실행하고 다음 결과를 반환합니다 -

ans =
   14

옥타브를 사용한 한계 계산

다음은 기호를 사용한 위 예의 옥타브 버전입니다. 패키지를 실행하고 결과를 비교하십시오 -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave는 위의 명령문을 실행하고 다음 결과를 반환합니다 -

ans =
   0.7142857142857142857

한계의 기본 속성 확인

대수 극한 정리는 극한의 몇 가지 기본 속성을 제공합니다. 다음과 같습니다 -

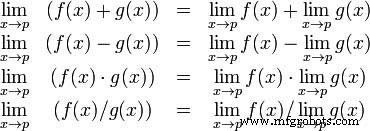
두 가지 기능을 고려해보자 -

• f(x) =(3x + 5)/(x - 3)
• g(x) =x ² + 1.

두 함수의 x가 5가 되는 함수의 극한을 계산하고 이 두 함수와 MATLAB을 사용하여 극한의 기본 속성을 확인합니다.

예시

스크립트 파일을 만들고 다음 코드를 입력하십시오 -

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

파일을 실행하면 -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

옥타브를 이용한 극한의 기본 속성 검증

다음은 기호를 사용한 위 예의 옥타브 버전입니다. 패키지를 실행하고 결과를 비교하십시오 -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave는 위의 명령문을 실행하고 다음 결과를 반환합니다 -

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

왼쪽 및 오른쪽 제한

함수에 변수의 특정 값에 대한 불연속성이 있는 경우 해당 지점에 한계가 존재하지 않습니다. 다시 말해, 함수 f(x)의 극한은 x =a에서 불연속성을 가지며, x가 왼쪽에서 x에 접근할 때 극한 값이 오른쪽에서 x에 접근할 때 극한 값과 같지 않을 때입니다.

이것은 왼손 및 오른손 한계의 개념으로 이어집니다. 왼쪽 극한은 x a의 극한으로 정의됩니다. 즉, x가 접근합니다. 오른쪽 극한은 x> a 값에 대해 오른쪽에서 x -> a의 극한으로 정의됩니다. 즉, x가 접근합니다. 좌극한과 우극한이 같지 않으면 극한이 존재하지 않습니다.

함수를 고려해보자 -

f(x) =(x - 3)/|x - 3|

lim_x->3 f(x)는 존재하지 않습니다. MATLAB은 두 가지 방법으로 이 사실을 확인하는 데 도움이 됩니다.

• 함수의 그래프를 표시하고 불연속성을 표시합니다.
• 한계를 계산하고 둘 다 다르다는 것을 보여줌.

왼쪽 및 오른쪽 제한은 문자열 'left' 및 'right'를 limit 명령에 마지막 인수로 전달하여 계산됩니다.

예시

스크립트 파일을 만들고 다음 코드를 입력하십시오 -

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

파일을 실행하면 MATLAB은 다음 플롯을 그립니다.

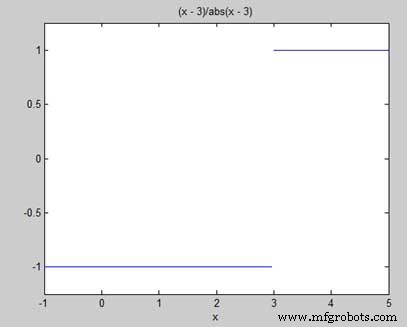
이 후 다음 출력이 표시됩니다 -

l =
   -1
  
r =
   1