MATLAB








MATLAB은 diff를 제공합니다. 기호 도함수를 계산하는 명령입니다. 가장 간단한 형태로 diff 명령어에 미분하고자 하는 함수를 인자로 전달하면 됩니다.
예를 들어, 함수 f(t) =3t 2 의 도함수를 계산해 보겠습니다. + 2t -2
스크립트 파일을 만들고 다음 코드를 입력하십시오 -
syms t f = 3*t^2 + 2*t^(-2); diff(f)
위의 코드를 컴파일하고 실행하면 다음과 같은 결과가 생성됩니다. -
ans = 6*t - 4/t^3
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
ans = -(4.0)*t^(-3.0)+(6.0)*t
함수의 미분을 위한 다양한 방정식이나 규칙을 간략하게 설명하고 이러한 규칙을 확인합니다. 이를 위해 1차 도함수에 대해 f'(x)를 작성하고 2차 도함수에 대해 f"(x)를 작성합니다.
다음은 차별화 규칙입니다 -
모든 함수 f와 g와 실수 a와 b는 함수의 도함수 -
h(x) =af(x) + bg(x) x에 대한 −
h'(x) =af'(x) + bg'(x)
합 및 빼기 규칙에 따르면 f와 g가 두 함수이고 f'와 g'는 각각 도함수이며,
(f + g)' =f' + g'
(f - g)' =f' - g'
제품 규칙에 따르면 f와 g가 두 함수이고 f'와 g'는 각각 도함수이며,
(f.g)' =f'.g + g'.f
몫 규칙에 따르면 f와 g가 두 함수이고 f'와 g'는 각각 도함수이며,
(f/g)' =(f'.g - g'.f)/g 2
다항식 또는 기본 거듭제곱 법칙은 y =f(x) =x n 인 경우 , f' =n. x (n-1)
이 규칙의 직접적인 결과는 상수의 미분이 0이라는 것입니다. 즉, y =k , 임의의 상수, 그 다음
f' =0
체인 규칙에 따르면 함수 h(x) =f(g(x))의 함수 미분 x에 대해,
h'(x)=f'(g(x)).g'(x)
스크립트 파일을 만들고 다음 코드를 입력하십시오 -
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
파일을 실행하면 MATLAB은 다음 결과를 표시합니다. -
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
다음 표는 일반적으로 사용되는 지수, 대수 및 삼각 함수의 도함수를 제공합니다 -
| 함수 | 파생 |
|---|---|
| c a.x | c a.x .ln c.a (ln은 자연 로그) |
| e x | e x |
| ln x | 1/x |
| lnc x | 1/x.ln c |
| x x | x x .(1 + ln x) |
| 죄(x) | cos(x) |
| cos(x) | -sin(x) |
| 탄(x) | 초 2 (x) 또는 1/cos 2 (x) 또는 1 + tan 2 (x) |
| 요람(x) | -csc 2 (x) 또는 -1/sin 2 (x) 또는 -(1 + 유아용 침대 2 (x)) |
| 초(x) | 초(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
스크립트 파일을 만들고 다음 코드를 입력하십시오 -
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
파일을 실행하면 MATLAB은 다음 결과를 표시합니다. -
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
함수 f의 더 높은 도함수를 계산하기 위해 diff(f,n) 구문을 사용합니다. .
함수 y =f(x) =x .e -3x 의 2차 도함수를 계산해 보겠습니다.
f = x*exp(-3*x); diff(f, 2)
MATLAB은 코드를 실행하고 다음 결과를 반환합니다. -
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
이 예에서는 문제를 해결해 보겠습니다. 주어진 함수 y =f(x) =3 sin(x) + 7 cos(5x) . f" + f =-5cos(2x) 방정식인지 알아내야 합니다. 사실입니다.
스크립트 파일을 만들고 다음 코드를 입력하십시오 -
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
파일을 실행하면 다음과 같은 결과가 표시됩니다. -
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
그래프의 지역 최대값과 최소값을 검색하는 경우 기본적으로 특정 지역에서 함수 그래프의 최고점 또는 최저점 또는 기호 변수의 특정 값 범위를 찾고 있습니다.
함수 y =f(x)의 경우 그래프에서 기울기가 0인 점을 정지점이라고 합니다. . 즉, 정지점은 f'(x) =0인 위치입니다.
미분하는 함수의 정지점을 찾으려면 도함수를 0으로 설정하고 방정식을 풀어야 합니다.
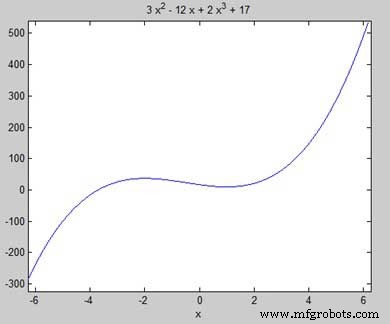
함수 f(x) =2x 3 의 정지점을 찾자 + 3x 2 − 12x + 17
다음 단계를 따르십시오 -
먼저 함수를 입력하고 그래프를 그려보겠습니다.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB은 코드를 실행하고 다음 플롯을 반환합니다 -
다음은 위의 예에 대한 Octave 등가 코드입니다. -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
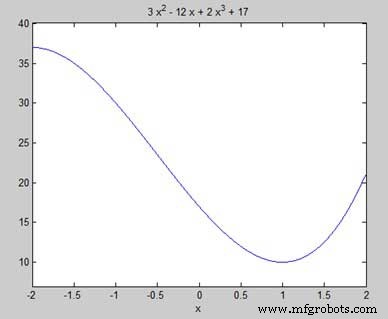
우리의 목표는 그래프에서 국소 최대값과 최소값을 찾는 것이므로 그래프에서 구간 [-2, 2]에 대한 국소 최대값과 최소값을 찾아보겠습니다.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB은 코드를 실행하고 다음 플롯을 반환합니다 -
다음은 위의 예에 대한 Octave 등가 코드입니다. -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
다음으로 도함수를 계산해 보겠습니다.
g = diff(y)
MATLAB은 코드를 실행하고 다음 결과를 반환합니다. -
g = 6*x^2 + 6*x - 12
다음은 위의 계산에 해당하는 Octave입니다. -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
미분 함수 g를 풀어서 0이 되는 값을 얻습니다.
s = solve(g)
MATLAB은 코드를 실행하고 다음 결과를 반환합니다. -
s = 1 -2
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave는 코드를 실행하고 다음 결과를 반환합니다 -
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
이것은 우리의 계획과 일치합니다. 따라서 임계점 x =1, -2에서 함수 f를 평가해 보겠습니다. subs를 사용하여 기호 함수의 값을 대체할 수 있습니다. 명령.
subs(y, 1), subs(y, -2)
MATLAB은 코드를 실행하고 다음 결과를 반환합니다. -
ans = 10 ans = 37
다음은 위의 계산에 해당하는 옥타브입니다 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
따라서 함수 f(x) =2x 3 의 최소값과 최대값은 + 3x 2 − 12x + 17, [-2,2] 구간에서 10과 37입니다.
MATLAB은 dsolve를 제공합니다. 미분방정식을 기호로 푸는 명령입니다.
dsolve의 가장 기본적인 형태 단일 방정식의 해를 찾는 명령은
dsolve('eqn')
여기서 eqn 방정식을 입력하는 데 사용되는 텍스트 문자열입니다.
MATLAB이 C1, C2 등으로 레이블을 지정하는 임의의 상수 세트가 있는 기호 솔루션을 반환합니다.
문제에 대한 초기 및 경계 조건을 −
와 같은 방정식 다음에 쉼표로 구분된 목록으로 지정할 수도 있습니다.
dsolve('eqn','cond1', 'cond2',…)
dsolve 명령을 사용하기 위해 도함수는 D로 표시됩니다. . 예를 들어 f'(t) =-2*f + cost(t)와 같은 방정식은 −
로 입력됩니다.'Df =-2*f + cos(t)'
더 높은 파생 상품은 파생 상품의 차수에 따라 D 다음에 표시됩니다.
예를 들어 방정식 f"(x) + 2f'(x) =5sin3x는 −
로 입력해야 합니다.'D2y + 2Dy =5*sin(3*x)'
1차 미분 방정식의 간단한 예를 들어보겠습니다. y' =5y.
s = dsolve('Dy = 5*y')
MATLAB은 코드를 실행하고 다음 결과를 반환합니다. -
s = C2*exp(5*t)
y" - y =0, y(0) =-1, y'(0) =2와 같은 2차 미분 방정식의 또 다른 예를 들어보겠습니다.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB은 코드를 실행하고 다음 결과를 반환합니다. -
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB
Simulink는 MATLAB과 통합된 동적 및 임베디드 시스템을 위한 시뮬레이션 및 모델 기반 설계 환경입니다. MathWorks에서 개발한 Simulink는 다중 도메인 동적 시스템을 모델링, 시뮬레이션 및 분석하기 위한 데이터 흐름 그래픽 프로그래밍 언어 도구입니다. 기본적으로 사용자 정의 가능한 블록 라이브러리 세트가 있는 그래픽 블록 다이어그램 도구입니다. 이를 통해 MATLAB 알고리즘을 모델에 통합하고 추가 분석을 위해 시뮬레이션 결과를 MATLAB으로 내보낼 수 있습니다. Simulink는 −를 지원합니다. 시스
Arduino 자습서 시리즈의 일곱 번째 Arduino 자습서에 오신 것을 환영합니다. 이 튜토리얼에서는 Arduino를 Matlab에 연결하는 방법과 직렬 포트를 사용하여 통신하는 방법을 배웁니다. 또한 Matlab을 사용하여 Arduino Board를 제어하는 예를 만들 것입니다. 이것은 따라하기 쉬운 단계별 비디오 자습서입니다. 또한 동영상 아래에서 이 튜토리얼에 필요한 부분과 동영상의 예제 소스 코드를 찾을 수 있습니다. 이 Arduino 튜토리얼에 필요한 구성요소 아두이노 보드 ..................