단순화를 위한 부울 규칙

부울 대수는 논리 회로의 단순화에서 가장 실용적인 용도를 찾습니다.

논리 회로의 기능을 기호(부울) 형식으로 변환하고 결과 방정식에 특정 대수 규칙을 적용하여 항 및/또는 산술 연산의 수를 줄이면 단순화된 방정식은 논리 회로가 수행하는 회로 형식으로 다시 번역될 수 있습니다. 더 적은 수의 구성 요소로 동일한 기능을 제공합니다.

더 적은 수의 부품으로 동등한 기능을 달성할 수 있다면 그 결과 신뢰성이 향상되고 제조 비용이 절감됩니다.

이를 위해 이 섹션에서는 표현식을 가장 단순한 형태로 줄이는 데 사용하기 위해 여러 부울 대수 규칙을 제시합니다.

이 장에서 이미 검토한 항등식과 속성은 부울 단순화에 매우 유용하며 대부분 "정상" 대수의 많은 항등식 및 속성과 유사합니다.

그러나 이 섹션에 표시된 규칙은 모두 부울 수학에만 적용됩니다.

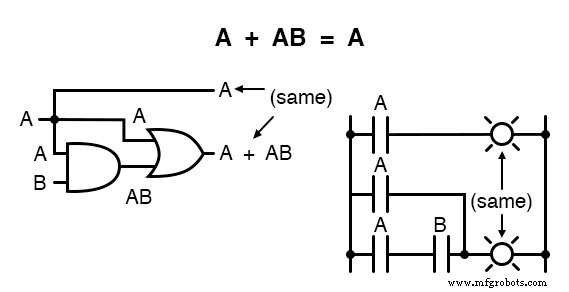
이 규칙은 두 항에서 "A"를 인수분해한 다음 A + 1 =1 및 1A =A의 규칙을 적용하여 최종 결과를 얻음으로써 상징적으로 증명할 수 있습니다.

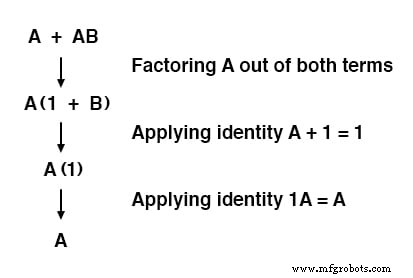
A + 1 =1 규칙을 사용하여 (B + 1) 항을 1로 줄이는 방법에 유의하십시오.

"A + 1 =1"과 같은 규칙이 문자 "A"를 사용하여 표현될 때 "A"를 포함하는 표현에만 적용된다는 의미는 아닙니다.

A + 1 =1과 같은 규칙에서 "A"가 나타내는 것은 모든 부울 변수 또는 변수 모음입니다.

이것은 아마도 신입생이 부울 단순화에서 마스터하기 가장 어려운 개념일 것입니다. 표준 형식이 아닌 표현식에 표준화된 ID, 속성 및 규칙을 적용하는 것입니다.

예를 들어, 부울 표현식 ABC + 1도 "A + 1 =1" 항등식을 통해 1로 줄어듭니다.

이 경우 ID 표준 형식의 "A" 용어가 원래 표현의 "ABC" 용어 전체를 나타낼 수 있음을 인식합니다.

다음 규칙은 이 섹션에 표시된 첫 번째 규칙과 유사해 보이지만 실제로는 상당히 다르며 더 영리한 증명이 필요합니다.

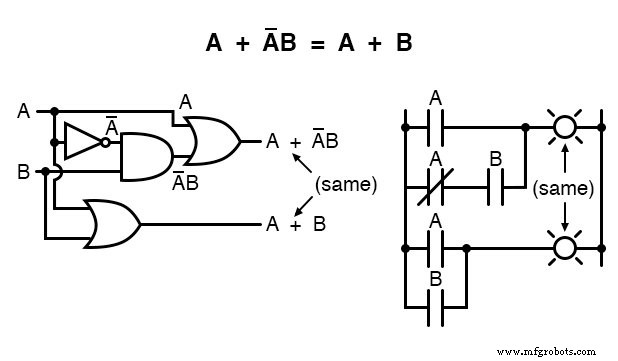
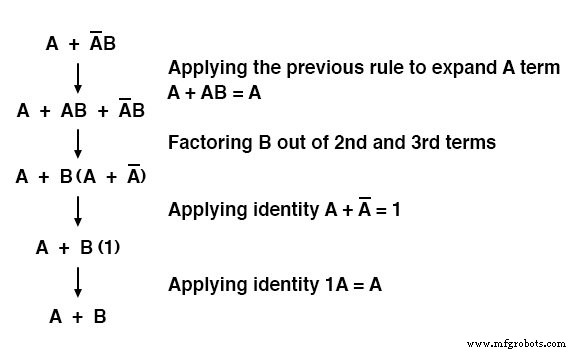
마지막 규칙(A + AB =A)을 사용하여 표현식의 첫 번째 "A" 용어를 "단순화 해제"하여 "A"를 "A + AB"로 변경하는 방법에 유의하십시오.

이것은 후진 단계처럼 보일 수 있지만 표현을 더 간단한 것으로 줄이는 데 확실히 도움이 되었습니다!

때때로 수학에서 우리는 가장 우아한 해를 얻기 위해 "뒤로" 단계를 밟아야 합니다.

체스 게임에서 승리하려면 거의 항상 계산된 희생이 필요하듯이, 그러한 단계를 밟아야 할 때와 하지 말아야 할 때를 아는 것은 대수학의 예술 형식의 일부입니다.

또 다른 규칙은 합산 표현식의 단순화와 관련이 있습니다.

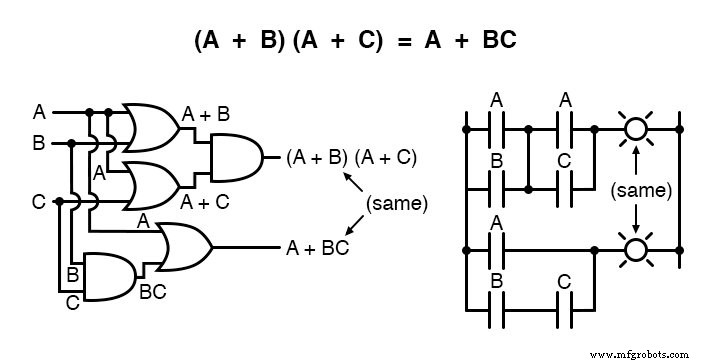
그리고 해당 증거:

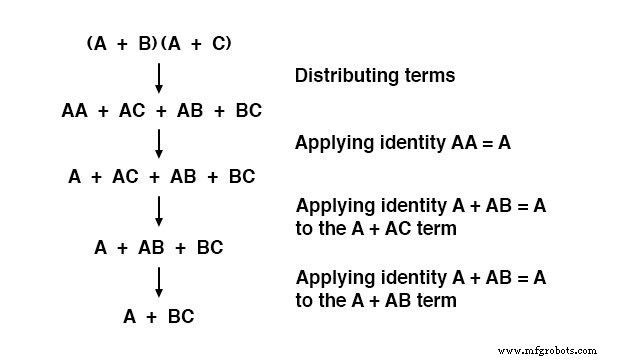
요약하자면 다음은 이 섹션에서 설명하는 부울 단순화의 세 가지 새로운 규칙입니다.

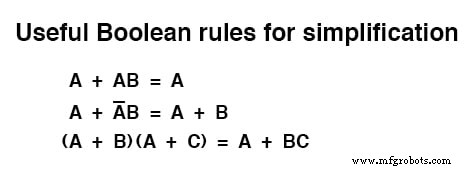
관련 워크시트:

<울>

부울 대수학 워크시트