Millman의 정리 재검토

각 분기에 직렬 저항과 전압 소스가 포함된 회로의 병렬 분기에 걸쳐 "Millman Voltage"를 결정하기 위한 이상한 방정식이 어디서 나온 것인지 궁금할 것입니다.

이 방정식의 일부는 이전에 본 방정식에 익숙합니다. 예를 들어, 큰 분수의 분모는 병렬 저항 방정식의 분모와 눈에 띄게 비슷해 보입니다. 그리고 물론, 큰 분수의 분자에 있는 E/R 항은 전류에 대한 수치를 제공해야 하며, 옴의 법칙은 그대로(I=E/R)입니다.

이제 Venin 및 Norton 소스 동등성을 다루었으므로 Millman의 방정식을 이해하는 데 필요한 도구가 있습니다. Millman의 방정식이 실제로 수행하는 것은 각 분기(직렬 전압 소스 및 저항 포함)를 Venin 등가 회로로 취급한 다음 각 분기를 등가 Norton 회로로 변환하는 것입니다.

테브냉 등가 회로

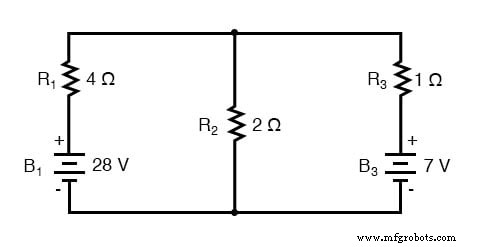
따라서 위의 회로에서 배터리 B1과 저항 R1은 4Ω 저항과 병렬로 7A(28V/4Ω)의 Norton 소스로 변환되는 Thevenin 소스로 보입니다. 가장 오른쪽 분기는 병렬로 7암페어 전류원(7볼트/1Ω)과 1Ω 저항으로 변환됩니다. 전압 소스가 전혀 포함되지 않은 중앙 분기는 2Ω 저항과 병렬로 0A의 Norton 소스로 변환됩니다.

Norton 등가 회로

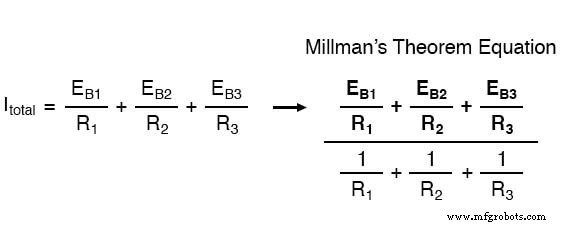
전류 소스는 각각의 전류를 병렬로 직접 추가하므로 총 회로 전류는 7 + 0 + 7 또는 14A가 됩니다. 이러한 Norton 소스 전류의 추가는 Millman 방정식의 분자로 표현되는 것입니다.

밀만 방정식

모든 Norton 저항은 등가 회로에서도 서로 병렬이므로 전체 저항을 생성하기 위해 감소합니다. 소스 저항의 이러한 감소는 Millman 방정식의 분모로 표현되는 것입니다.

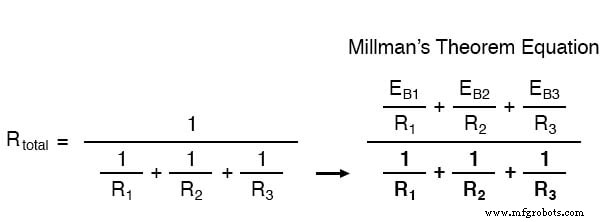
이 경우 저항 총계는 571.43mΩ(571.43mΩ)입니다. 이제 단일 Norton 전류 소스와 Norton 저항을 사용하여 등가 회로를 다시 그릴 수 있습니다.

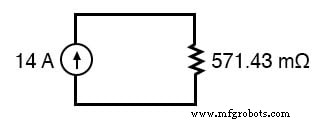
옴의 법칙은 이제 이 두 구성 요소의 전압을 알려줄 수 있습니다(E=IR).

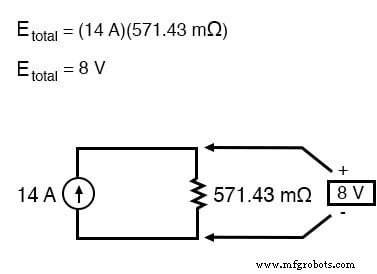
지금까지 회로에 대해 알고 있는 내용을 요약해 보겠습니다. 우리는 이 회로의 총 전류가 모든 분기 전압의 합을 각각의 저항으로 나눈 값이라는 것을 알고 있습니다. 우리는 또한 모든 분기 저항의 역수를 취하여 총 저항을 구한다는 것을 알고 있습니다. 또한 모든 분기에 걸친 총 전압은 총 전류에 총 저항(E=IR)을 곱하여 찾을 수 있다는 사실을 잘 알고 있어야 합니다. 우리가 해야 할 일은 총 회로 전류와 총 저항에 대해 이전에 가졌던 두 가지 방정식을 합치고 곱하여 총 전압을 찾는 것입니다.

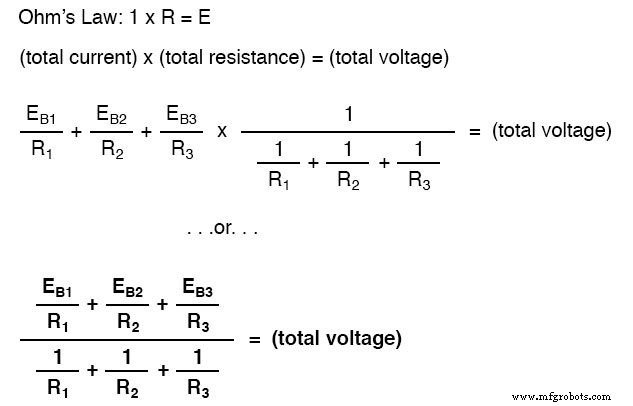
Millman의 방정식은 회로의 모든 분기에서 총 전압을 찾기 위해 병렬 저항 공식과 함께 Thevenin-Norton 변환을 일치시킨 것입니다. 이제 미스터리의 일부가 사라졌으면 합니다!

관련 워크시트: