MATLAB - 통합

통합은 본질적으로 다른 두 가지 유형의 문제를 다룹니다.

• 첫 번째 유형에서는 함수의 도함수가 제공되고 함수를 찾고자 합니다. 따라서 우리는 기본적으로 차별화 과정을 역전시킵니다. 이 역 과정을 반미분 또는 원시 함수 찾기 또는 무한 적분 찾기라고 합니다. .

• 두 번째 유형의 문제는 매우 많은 수의 매우 작은 양을 더한 다음 양의 크기가 0에 가까워지면 극한을 취하는 반면 항의 수는 무한대가 되는 경향이 있습니다. 이 프로세스는 정적분의 정의로 이어집니다. .

한정적분은 면적, 부피, 무게 중심, 관성 모멘트, 힘에 의해 한 일 및 기타 다양한 응용 분야를 찾는 데 사용됩니다.

MATLAB을 사용하여 무한 적분 구하기

정의에 따르면, 함수 f(x)의 도함수가 f'(x)이면 x에 대한 f'(x)의 무한 적분은 f(x)라고 합니다. 예를 들어, x ² 의 도함수(x에 대한) 때문에 2x인 경우 2x의 무한 적분은 x ² 라고 말할 수 있습니다. .

기호 -

f'(x ² ) =2배 따라서

∫ 2xdx =x ² .

무한 적분은 x ² 의 도함수이므로 고유하지 않습니다. + c는 상수 c의 값에 대해 2배가 됩니다.

이것은 기호로 -

로 표현됩니다.

∫ 2xdx =x ² + c .

여기서 c는 '임의 상수'라고 합니다.

MATLAB은 int 식의 적분을 계산하는 명령입니다. 함수의 무한 적분에 대한 식을 유도하기 위해 다음과 같이 작성합니다. -

int(f);

예를 들어, 이전 예에서 -

syms x 
int(2*x)

MATLAB은 위의 명령문을 실행하고 다음 결과를 반환합니다. -

ans =
   x^2

예시 1

이 예에서는 일반적으로 사용되는 몇 가지 표현식의 적분을 구해 보겠습니다. 스크립트 파일을 만들고 그 안에 다음 코드를 입력하십시오 -

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

파일을 실행하면 다음과 같은 결과가 표시됩니다. -

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

예시 2

스크립트 파일을 만들고 그 안에 다음 코드를 입력하십시오 -

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))

int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))

int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

예쁘다 함수는 더 읽기 쉬운 형식으로 표현식을 반환합니다.

파일을 실행하면 다음과 같은 결과가 표시됩니다. -

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

MATLAB을 사용하여 정의 적분 구하기

정의에 따르면, 정적분은 기본적으로 합계의 극한입니다. 우리는 한정적분을 사용하여 곡선과 x축 사이의 면적과 두 곡선 사이의 면적과 같은 면적을 찾습니다. 한정 적분은 필요한 양이 합계의 한계로 표현될 수 있는 다른 상황에서도 사용할 수 있습니다.

int 함수는 적분을 계산하려는 한계를 전달하여 명확한 적분에 사용할 수 있습니다.

계산하려면

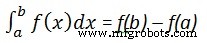
우리는 씁니다,

int(x, a, b)

예를 들어 다음 값을 계산하려면 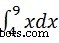씁니다 -

int(x, 4, 9)

MATLAB은 위의 명령문을 실행하고 다음 결과를 반환합니다. -

ans =
   65/2

다음은 위의 계산에 해당하는 옥타브입니다 -

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave는 코드를 실행하고 다음 결과를 반환합니다 -

Area: 

   32.500

다음과 같이 Octave에서 제공하는 quad() 함수를 사용하여 대체 솔루션을 제공할 수 있습니다.

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave는 코드를 실행하고 다음 결과를 반환합니다 -

Area: 
   32.500

예시 1

x축과 곡선 y =x ³ 사이에 둘러싸인 면적을 계산해 보겠습니다. −2x+5 및 좌표 x =1 및 x =2.

필요한 영역은 −

로 지정됩니다.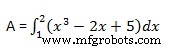

스크립트 파일을 만들고 다음 코드를 입력하십시오 -

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

파일을 실행하면 다음과 같은 결과가 표시됩니다. -

a =
23/4
Area: 
   5.7500

다음은 위의 계산에 해당하는 옥타브입니다 -

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave는 코드를 실행하고 다음 결과를 반환합니다 -

Area: 

   5.7500

다음과 같이 Octave에서 제공하는 quad() 함수를 사용하여 대체 솔루션을 제공할 수 있습니다.

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave는 코드를 실행하고 다음 결과를 반환합니다 -

Area: 
   5.7500

예시 2

곡선 아래의 면적 찾기:f(x) =x ² -4 ≤ x ≤ 9에 대한 cos(x).

스크립트 파일을 만들고 다음 코드를 작성하십시오 -

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

파일을 실행하면 MATLAB이 그래프를 플로팅합니다 -

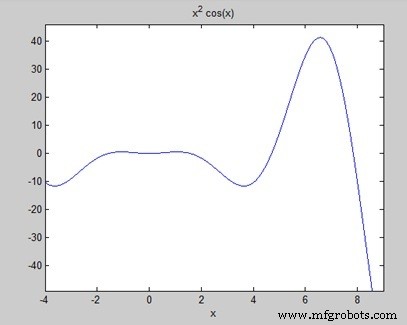
출력은 다음과 같습니다 -

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

다음은 위의 계산에 해당하는 옥타브입니다 -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));