음수 이진수

덧셈이 쉽게 이루어지므로 숫자 중 하나를 음수로 만들기만 하면 동일한 기술로 뺄셈 연산을 수행할 수 있습니다. 예를 들어, 7 - 5의 빼기 문제는 기본적으로 더하기 문제 7 + (-5)와 동일합니다.

양수를 이진수로 나타내는 방법을 이미 알고 있으므로 이제 음수를 나타내는 방법만 알면 뺄 수 있습니다.

일반적으로 위의 예에서와 같이 -5를 사용하여 최상위 자릿수 바로 왼쪽에 빼기 기호를 배치하여 음수 십진수를 나타냅니다. 그러나 이진 표기법을 사용하는 전체 목적은 비트 값을 전압으로 나타낼 수 있는 온/오프 회로를 구성하는 것입니다(2개의 대체 값:"높음" 또는 "낮음").

이 컨텍스트에서 "빼기" 기호와 같은 세 번째 기호는 사치스럽지 않습니다. 이러한 회로는 켜짐 또는 꺼짐(두 가지 가능한 상태)만 가능하기 때문입니다. 한 가지 해결책은 수학 기호를 나타내는 것 외에는 아무것도 하지 않는 비트(회로)를 예약하는 것입니다.

보시다시피 표준 자리 가중치 값 이외의 다른 목적으로 비트를 사용하기 시작할 때 주의해야 합니다. 그렇지 않으면 1101₂ 실제로 음수 5를 나타내려는 경우 숫자 13으로 잘못 해석될 수 있습니다.

여기서 일을 바로 잡기 위해 먼저 처리할 가장 큰 숫자를 나타내는 데 필요한 비트 수를 결정한 다음 산술 연산에서 해당 비트 필드 길이를 초과하지 않도록 해야 합니다.

위의 예에서는 음수 7(1111₂ ) ~ 양수 7(0111₂ ), 네 번째 비트를 "기호" 비트로 만들어 더 이상 사용하지 않습니다. 이러한 제한을 먼저 설정해야만 음수와 더 큰 양수를 혼동하는 것을 피할 수 있습니다.

음수 5를 1101₂로 나타냄 음수 이진법의 부호-크기 시스템의 예입니다. 맨 왼쪽 비트를 자리 가중치가 아닌 부호 표시기로 사용하여 실제적인 이점을 제공하는 "순수한" 형태의 이진 표기법을 희생하고 있습니다. 바로 음수 표현입니다.

맨 왼쪽 비트는 양수 또는 음수 부호로 읽고 나머지 비트는 표준 이진 표기법에 따라 해석됩니다. 왼쪽에서 오른쪽으로 가중치를 2의 배수로 배치합니다.

보완

부호-크기 접근 방식은 간단하지만 산술 목적으로는 그다지 실용적이지 않습니다. 예를 들어, 어떻게 마이너스 5를 추가합니까(1101₂ ) 이진 덧셈에 대한 표준 기술을 사용하여 다른 숫자로?

덧셈이 작동하려면 덧셈을 수행하는 새로운 방법을 발명해야 하고 그렇게 하면 장수 뺄셈으로 작업을 수행하는 것이 좋습니다. 부호 크기 계산과 함께 수행해야 하는 경우 덧셈을 통해 뺄셈을 수행하기 위해 음수를 사용하는 것은 산술적 이점이 없으며 그것이 우리의 목표였습니다!

음수를 나타내는 또 다른 방법이 있습니다. 장수 덧셈의 친숙한 기술이며 또한 보완이라고 하는 자릿수 가중 계산 관점에서 더 의미가 있습니다.

이 전략을 사용하면 부호-크기 접근 방식에서와 마찬가지로 특수 목적을 위해 맨 왼쪽 비트를 할당하여 이전과 같이 숫자 제한을 정의합니다. 그러나 이번에는 맨 왼쪽 비트가 단순한 부호 비트 이상입니다. 오히려 음의 자리 가중치 값을 갖습니다. 예를 들어 음수 5의 값은 다음과 같이 표시됩니다.

<사전>

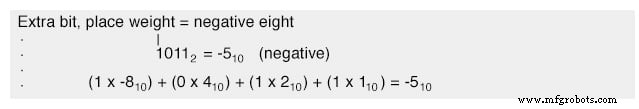
오른쪽 3비트는 0에서 7까지의 크기를 나타낼 수 있고 맨 왼쪽 비트는 0 또는 음의 8을 나타내므로 음의 7(1001₂ =-8₁₀ + 1₂ =-7₁₀ ) ~ 양수 7(0111₂ =0₁₀ + 7₁₀ =7₁₀ ).

이 체계에서 양수를 나타내는 것(네 번째 비트가 음의 가중치로 지정됨)은 일반적인 이진 표기법과 다르지 않습니다. 그러나 음수를 나타내는 것은 그리 간단하지 않습니다.

<사전>

오른쪽 열의 음수 이진수는 오른쪽 세 비트의 합계와 가장 왼쪽 비트의 음수 8을 합한 것이며 왼쪽 열의 양수 이진수와 같은 진행 방식으로 "계산"하지 않습니다.

오히려 오른쪽 3비트는 가장 왼쪽 비트의 음수 8자리 값과 합할 때 원하는(음수) 합계와 같도록 적절한 값으로 설정해야 합니다.

2의 보수

그 오른쪽 3비트를 해당 양수의 2의 보수라고 합니다. 다음 비교를 고려하십시오.

<사전>

이 경우 음수 가중치 비트가 네 번째 비트(음수 8의 자리 값)인 경우 양수에 대한 2의 보수는 양수 값을 음수 값으로 만들기 위해 음수 8에 더하는 데 필요한 값입니다.

고맙게도 모든 이진수에 대한 2의 보수를 알아내는 쉬운 방법이 있습니다. 단순히 해당 숫자의 모든 비트를 반전하고 모든 1을 0으로 또는 그 반대로 변경한 다음(1의 보수라고 하는 것에 도달하기 위해) 1을 더합니다! 예를 들어, 5의 2의 보수를 구하려면(101₂ ), 먼저 모든 비트를 반전하여 010₂를 얻습니다. ("1의 보수"), 1을 더하여 011₂를 얻습니다. , 또는 -5₁₀ 3비트, 2의 보수 형식

흥미롭게도 이진수의 2의 보수를 생성하는 것은 크기 비트와 동시에 맨 왼쪽(부호) 비트를 포함하여 모든 비트를 조작하는 경우 동일하게 작동합니다. 양수 5를 음수 5로 변환하지만 4비트 모두에 대해 보완 프로세스를 수행하여 앞의 예에서 이것을 시도해 보겠습니다.

원래 숫자에 0(양수) 부호 비트를 포함해야 합니다. 5(0101₂ ). 먼저 모든 비트를 반전하여 1의 보수를 얻습니다. 1010₂ . 그런 다음 하나를 추가하면 최종 답인 1011₂를 얻습니다. , 또는 -5₁₀ 4비트, 2의 보수 형식으로 표현됩니다.

2의 보수 변환이 수행되기 전에 음수 가중치 비트의 위치가 이미 결정되어야 함을 기억하는 것이 매우 중요합니다. 이진 계산 필드가 여덟 번째 비트가 음수 가중치 비트(10000000₂ ), 다른 7개 비트 모두를 기반으로 2의 보수를 결정해야 합니다.

여기에서 5의 2의 보수(0000101₂ ) 1111011₂ . 이 시스템에서 양수 5는 00000101₂로 표시됩니다. , 11111011₂로 음수 5 .

관련 워크시트:

<울>

이진 수학 워크시트