메시 현재 방법 및 분석

메시 전류 방식 , 루프 현재 방법이라고도 함 는 연립방정식, Kirchhoff의 전압 법칙 및 옴의 법칙을 사용하여 네트워크에서 알려지지 않은 전류를 결정한다는 점에서 분기 전류 방법과 매우 유사합니다. 이는 Branch Current 방법과 다릅니다. 않습니다 Kirchhoff의 전류 법칙을 사용하면 일반적으로 알려지지 않은 변수와 연립 방정식이 적은 회로를 풀 수 있습니다. 이는 계산기 없이 강제로 풀어야 하는 경우에 특히 좋습니다.

메시 전류, 기존 방식

이 방법이 동일한 예제 문제에서 어떻게 작동하는지 봅시다:

루프 식별

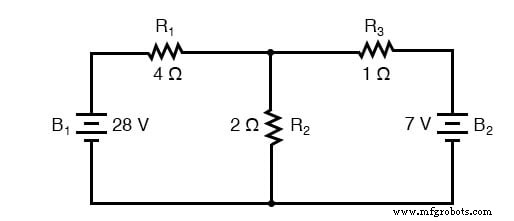
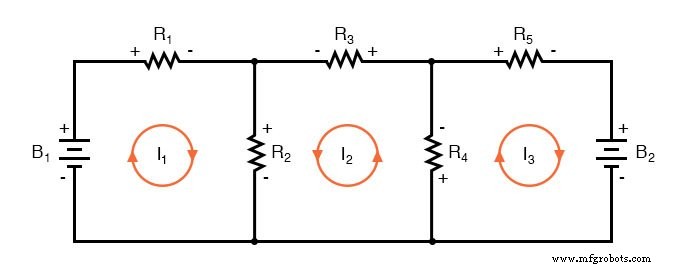
메쉬 전류 방법의 첫 번째 단계는 모든 구성 요소를 포함하는 회로 내에서 "루프"를 식별하는 것입니다. 예제 회로에서 B₁에 의해 형성된 루프 , R₁ , 및 R₂ B₂에 의해 형성된 루프 중 첫 번째가 됩니다. , R₂ , 및 R₃ 두 번째 것입니다. Mesh Current 방법의 가장 이상한 부분은 각 루프에서 순환하는 전류를 상상하는 것입니다. 사실, 이 방법은 회전하는 기어 세트와 같은 루프 사이에서 함께 맞물리는 이러한 전류의 아이디어에서 이름을 얻었습니다.

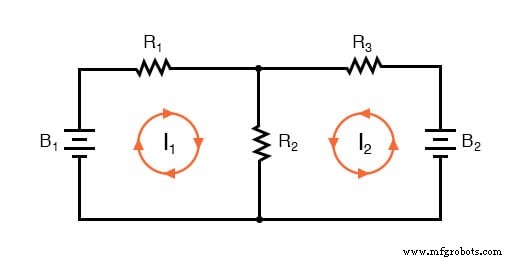
분기 전류 방법에서와 같이 각 전류의 방향을 선택하는 것은 완전히 임의적이지만 전류가 교차하는 구성 요소를 통해 같은 방향으로 가는 경우 결과 방정식을 더 쉽게 풀 수 있습니다(전류 I₁ 그리고 나₂ 둘 다 저항 R₂를 통해 "업"됩니다. , "메쉬" 또는 교차). 메쉬 전류의 가정된 방향이 잘못된 경우 해당 전류에 대한 대답은 음수 값을 갖습니다.

전압 강하 극성에 레이블 지정

다음 단계는 메쉬 전류의 가정된 방향에 따라 저항에 걸친 모든 전압 강하 극성에 레이블을 지정하는 것입니다. 전자가 음전하를 띠기 때문에 저항기의 "업스트림" 끝은 항상 음이고 저항기의 "다운스트림" 끝은 서로에 대해 양수임을 기억하십시오. 물론 배터리 극성은 다이어그램에서 기호 방향에 따라 결정되며 저항 극성(가정 전류 방향)과 "일치"하거나 "일치하지" 않을 수 있습니다.

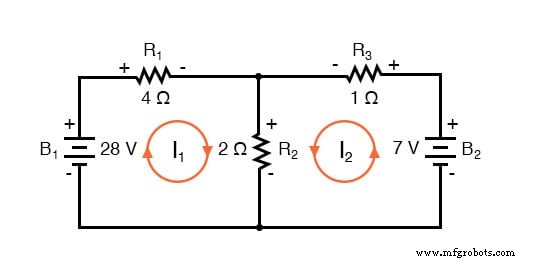
Kirchhoff의 전압 법칙을 사용하여 이제 이러한 각 루프를 둘러보고 구성 요소 전압 강하 및 극성을 나타내는 방정식을 생성할 수 있습니다. 분기 전류 방법과 마찬가지로 저항의 전압 강하를 저항(옴 단위)과 해당 메쉬 전류(이 시점에서 알 수 없는 양)의 곱으로 표시합니다. 두 전류가 서로 맞물리는 경우 저항 전류가 합인 방정식에 해당 항을 씁니다. 두 개의 맞물림 전류 중.

방정식을 사용하여 회로의 왼쪽 루프 추적

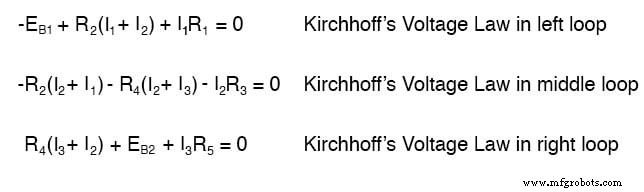
왼쪽 상단 모서리에서 시작하여 시계 반대 방향으로 이동하는 회로의 왼쪽 루프 추적(시작 지점과 방향 선택은 궁극적으로 관련이 없음), 마치 전압계를 손에 들고 있는 것처럼 극성을 계산하고 앞 지점에 빨간색 리드 그리고 뒤에 있는 점에 검은색 리드가 있으면 다음 방정식을 얻습니다.

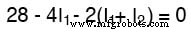
방정식의 중간 항은 메쉬 전류 I₁의 합을 사용합니다. 그리고 나₂ 저항 R₂를 통한 전류로 . 메쉬 전류 I₁ 그리고 나₂ R₂를 통해 같은 방향으로 가고 있습니다. , 따라서 서로를 보완합니다. I₁에 2의 계수 분포 그리고 나₂ 용어, I₁ 결합 방정식의 항을 다음과 같이 단순화할 수 있습니다.

현재 두 개의 미지수가 있는 하나의 방정식이 있습니다. 두 개의 미지의 메쉬 전류를 풀 수 있으려면 두 개의 방정식이 있어야 합니다. 회로의 다른 루프를 추적하면 다른 KVL 방정식을 얻을 수 있고 두 전류를 풀기에 충분한 데이터를 얻을 수 있습니다. 습관의 생물, 오른쪽 루프의 왼쪽 상단 모서리에서 시작하여 시계 반대 방향으로 추적합니다.

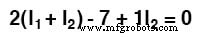
이전과 같이 방정식을 단순화하면 다음과 같이 끝납니다.

미지의 문제 해결

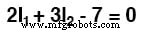
이제 두 개의 방정식을 사용하여 여러 방법 중 하나를 사용하여 미지의 전류 I₁를 수학적으로 해결할 수 있습니다. 그리고 나₂ :

회로 다시 그리기

이러한 솔루션이 mesh에 대한 가치임을 알고 있습니다. 가지가 아닌 현재 전류가 흐르면 다이어그램으로 돌아가서 모든 구성 요소에 전류를 흐르게 하기 위해 서로 어떻게 맞는지 확인해야 합니다.

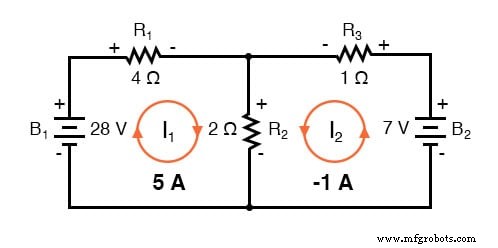
I₂에 대한 -1 amp의 솔루션 이는 우리가 처음에 전류의 방향이 잘못되었다고 가정했음을 의미합니다. 실제로 나는₂ (양수) 1 amp의 값에서 시계 반대 방향으로 흐르고 있습니다.

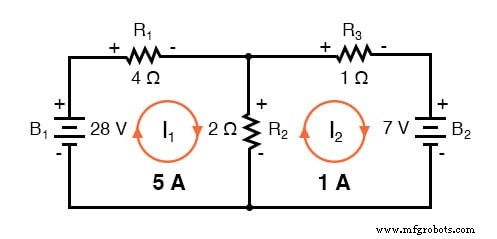
처음 가정한 것에서 전류 방향을 변경하면 R₂에 걸친 전압 강하의 극성이 변경됩니다. 및 R₃ 현재 I₂로 인해 . 여기에서 R₁을 통한 전류가 R₁ 양단의 전압 강하는 5A입니다. 전류와 저항(E=IR)의 곱, 20볼트(왼쪽에 양수, 오른쪽에 음수).

또한 R₃을 통한 전류는 다음과 같이 안전하게 말할 수 있습니다. 전압 강하가 1볼트(E=IR)인 1암페어, 왼쪽이 양수이고 오른쪽이 음수입니다. 그러나 R₂에서 무슨 일이 일어나고 있습니까? ?

메시 전류 I₁ R₂를 통해 "아래로" 가고 있습니다. , 메쉬 전류 I₂ 동안 R₂를 통해 "위로" 올라가고 있습니다. . R₂를 통해 실제 전류를 결정하려면 , 메쉬 전류 I₁ 그리고 나₂ 상호 작용(이 경우 서로 반대임)하고 대수적으로 더하여 최종 값에 도달합니다. 나는₁ 이후로 5암페어에서 "아래로" 가고 I₂ 진짜 1암페어에서 "업"됩니다. R₂를 통한 전류 "아래로" 내려가는 4암페어의 값이어야 합니다.

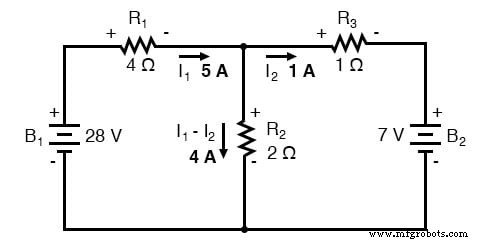
R₂를 통한 4A의 전류 2Ω의 저항은 8볼트(E=IR)의 전압 강하를 제공하며 위쪽은 양수, 아래쪽은 음수입니다.

메시 전류 분석의 장점

메쉬 전류 분석의 주요 이점은 일반적으로 더 적은 미지 값과 더 적은 연립 방정식을 사용하여 대규모 네트워크의 솔루션을 허용한다는 것입니다. 우리의 예제 문제는 분기 전류 방법을 풀기 위해 3개의 방정식을 사용하고 메시 전류 방법을 사용하는 2개의 방정식만 사용했습니다. 이 이점은 네트워크가 복잡해짐에 따라 훨씬 더 커집니다.

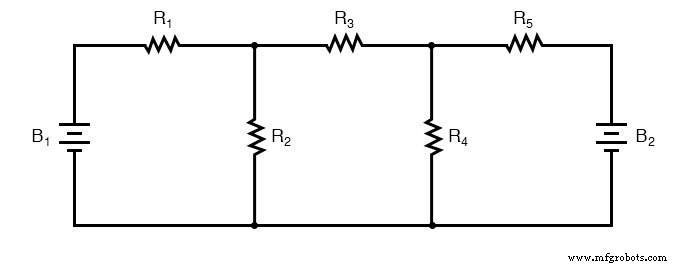
분기 전류를 사용하여 이 네트워크를 해결하려면 회로의 모든 고유한 전류(I₁ I₅를 통해 ). 이를 위해서는 2개의 KCL 방정식과 3개의 KVL 방정식(노드에서 KCL에 대한 2개의 방정식, 각 루프에서 KVL에 대한 3개의 방정식)의 형태로 솔루션에 대해 5개의 방정식이 필요합니다.

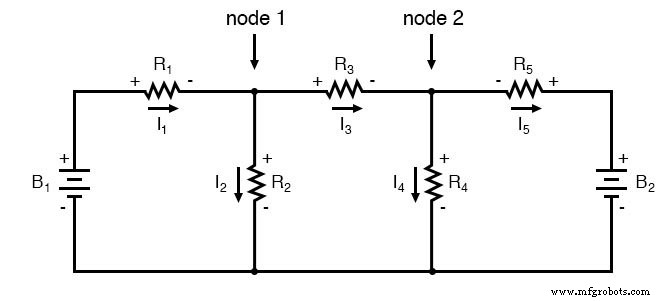
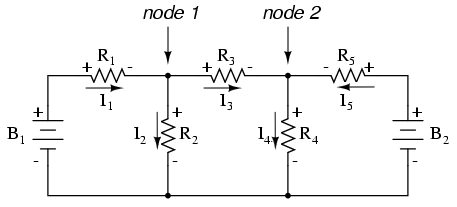
5개의 방정식으로 5개의 미지의 변수를 푸는 것보다 시간을 할애할 일이 없다면 이 회로에 대한 분기 전류 분석 방법을 사용해도 괜찮을 것입니다. 이 있는 사람들을 위해 우리 시대에 더 나은 일이지만, Mesh Current 방법은 훨씬 더 쉬워 3개의 미지수와 3개의 방정식만 풀면 됩니다.

작업할 방정식이 적다는 것은 특히 계산기 없이 손으로 연립 방정식 풀이를 수행할 때 결정적인 이점입니다.

불균형 휘트스톤 브리지

메시 전류에 적합한 또 다른 유형의 회로는 불균형 휘트스톤 브리지입니다. 이 회로를 예로 들어 보겠습니다.

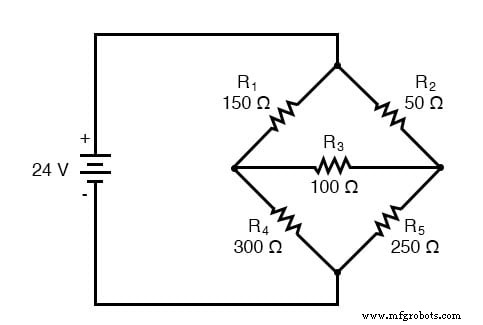
R₁의 비율 이후 /R₄ 및 R₂ /R₅ 같지 않으면 저항 R₃ 양단에 전압이 있다는 것을 알고 있습니다. , 그리고 그것을 통해 약간의 전류. 이 장의 시작 부분에서 논의한 바와 같이 이러한 유형의 회로는 일반적인 직렬 병렬 분석으로 환원할 수 없으며 다른 방법으로만 분석할 수 있습니다.

분기 전류 방법을 이 회로에 적용할 수 있지만 6 전류(I₁ I₆을(를) 통해 ), 풀기 위해 연립 방정식의 매우 큰 집합으로 이어집니다. 그러나 Mesh Current 방법을 사용하면 훨씬 적은 수의 변수로 모든 전류와 전압을 풀 수 있습니다.

메쉬 그리기

메쉬 전류 방법의 첫 번째 단계는 회로의 모든 구성 요소를 설명하기에 충분한 메쉬 전류를 끌어내는 것입니다. 브리지 회로를 보면 다음 전류 중 두 개를 어디에 배치해야 하는지 명확해야 합니다.

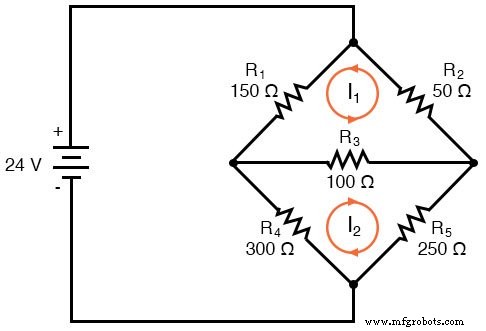
물론 이러한 메쉬 전류의 방향은 임의적입니다. 그러나 I₁ 나도₂ 배터리를 통과합니다. 따라서 세 번째 메쉬 전류 I₃를 추가해야 합니다. :

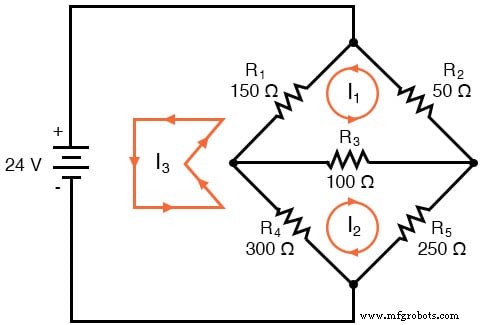
여기서는 I₃을 선택했습니다. R₄를 통해 배터리 하단에서 루프 , R₁을 통해 , 배터리 상단으로 돌아갑니다. 이것은 내가 I₃을 위해 선택할 수 있는 유일한 경로가 아닙니다. , 하지만 가장 간단해 보입니다.

저항기 전압 강하 극성에 레이블 지정

이제 가정된 각 전류의 방향에 따라 저항 전압 강하 극성에 레이블을 지정해야 합니다.

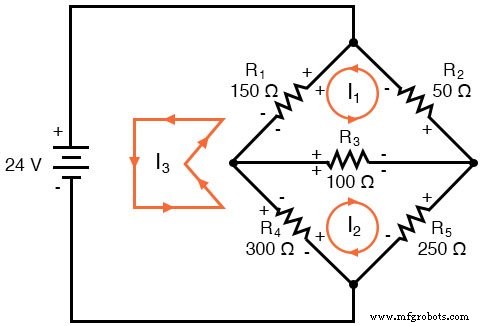
여기에서 매우 중요한 것을 알 수 있습니다. 저항 R₄에서 , 각각의 메쉬 전류에 대한 극성이 일치하지 않습니다. 그 메쉬 전류(I₂ 그리고 나₃ ) R₄를 거치고 있습니다. 다른 방향으로. 이것은 Mesh Current 분석 방법의 사용을 배제하지 않지만 약간 복잡합니다. 나중에 R₄를 피하는 방법을 보여줄 것입니다. 현재 충돌. (아래 예 참조)

KVL 사용

상단 노드에서 시작하여 시계 방향으로 추적하여 브리지의 상단 루프에 대한 KVL 방정식 생성:

이 방정식에서 우리는 전류의 일반적인 방향을 합으로 나타냅니다. 공통 저항을 통해. 예를 들어, 저항 R₃ , 값이 100Ω인 경우 위의 KVL 방정식에서 전압 강하는 100(I₁ + 나₂ ), 두 전류 모두 I₁ 그리고 나₂ R₃ 통과 오른쪽에서 왼쪽으로. 저항 R₁에 대해서도 마찬가지입니다. , 전압 강하 표현식이 150(I₁ + 나₃ ), I₁ 그리고 나₃ 저항을 통해 아래에서 위로 이동하여 함께 작동합니다. 전압 강하를 생성합니다.

브리지의 하단 루프에 대한 KVL 방정식을 생성하는 것은 저항 R₄을 통해 서로 반대 방향으로 흐르는 두 개의 전류가 있기 때문에 그리 쉽지 않습니다. . 다음은 내가 수행하는 방법입니다(오른쪽 노드에서 시작하여 시계 반대 방향으로 추적).

방정식의 원래 형식에서 두 번째 항이 저항 R₄를 갖는 방법에 유의하십시오. 차이를 곱한 300Ω의 값 I₂ 사이 그리고 나₃ (나는₂ - 나₃ ). 이것이 동일한 구성 요소를 통해 반대 방향으로 흐르는 두 개의 메쉬 전류의 결합된 효과를 나타내는 방법입니다. 여기서 적절한 수학적 기호를 선택하는 것이 매우 중요합니다. 300(I₂ - 나₃ )는 300(I₃)과 같은 의미가 아닙니다. - 나₂ ). 300(I₂ - 나₃ ) I₂를 먼저 생각했기 때문에 의 효과(양의 전압 강하 생성, R₄에 걸쳐 가상의 전압계로 측정) , 하단에 빨간색 리드, 상단에 검은색 리드), 그리고 두 번째로 I₃ 의 효과(음의 전압 강하 생성, 하단에 빨간색 리드, 상단에 검은색 리드 생성). 내가 ₃의 관점에서 생각했다면 의 효과가 먼저이고 I₂ '의 효과가 두 번째로, 가상의 전압계 리드를 동일한 위치(하단에 빨간색, 상단에 검정색)를 유지하면 표현식은 -300(I₃ - 나₂ ). 이 표현은 이다 수학적으로 첫 번째 것과 동일:+300(I₂ - 나₃ ).

글쎄, 그것은 두 개의 방정식을 처리하지만 세 개의 변수, 세 개의 방정식으로 구성된 연립 방정식 세트를 완성하려면 여전히 세 번째 방정식이 필요합니다. 이 세 번째 방정식에는 배터리 전압도 포함되어야 하며, 이 전압은 지금까지 이전 KVL 방정식 중 두 가지에 나타나지 않습니다. 이 방정식을 생성하기 위해 배터리의 하단(음) 단자에서 시작하여 시계 방향으로 이동하면서 가상의 전압계로 루프를 다시 추적합니다(다시 말하지만, 내가 밟는 방향은 임의적이며 방향과 같을 필요는 없습니다. 해당 루프의 메쉬 전류):

해류 해결

I₁ 풀기 , 나₂ , 그리고 나₃ 우리가 선호하는 연립 방정식 방법을 사용하여:

예: Octave를 사용하여 I₁에 대한 솔루션 찾기 , 나₂ , 그리고 나₃ 위의 단순화된 형태의 방정식에서.

해결책: 오픈 소스 Matlab® 클론인 Octave에서 열 요소가 쉼표로 구분되고 행이 세미콜론으로 구분된 대괄호 사이의 A 행렬에 계수를 입력합니다. 열 벡터에 전압을 입력합니다. b. 알 수 없는 전류:I₁ , ₂ , 그리고 나₃ x=A\b 명령에 의해 계산됩니다. 이는 x 열 벡터 내에 포함됩니다.

<사전> 옥타브:1>A =[300,100,150;100,650,-300;-150,300,-450] A =300 100 150 100 650 -300 -150 300 -450 옥타브:2> b =[0;0;-24] b =0 0 -24 옥타브:3> x =A\b x =-0.093793 0.077241 0.136092

I₁에 대해 음수 값에 도달했습니다. 그 메쉬 전류에 대해 가정된 방향이 잘못되었음을 알려줍니다. 따라서 각 저항을 통한 실제 전류 값은 다음과 같습니다.

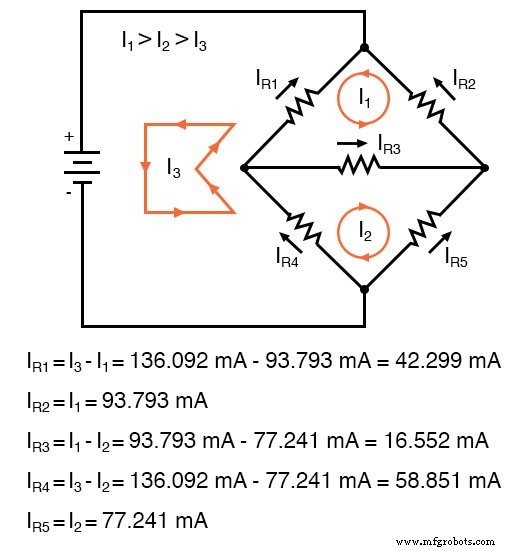
각 저항의 전압 강하 계산:

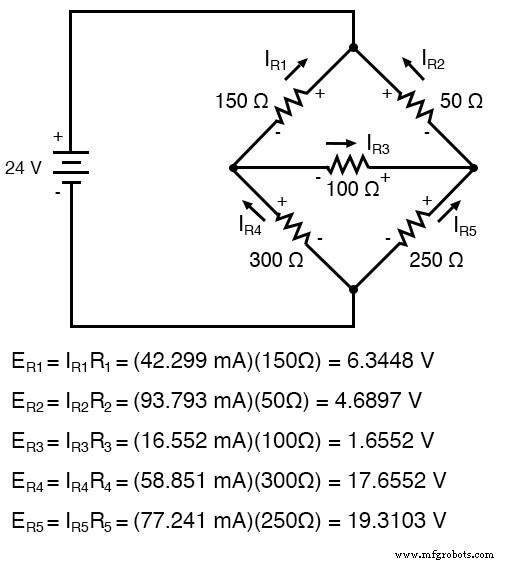
SPICE 시뮬레이션은 전압 계산의 정확성을 확인합니다.

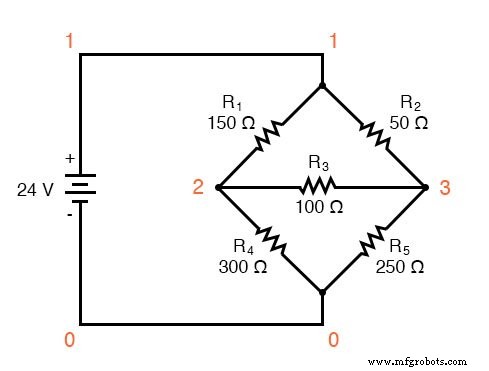
언밸런스드 휘트스톤 브리지 v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .끝 v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01 

예:

(a) 현재 I₃에 대한 새 경로 찾기 I₁과 비교하여 어떤 저항에서도 충돌하는 극성을 생성하지 않습니다. 또는 나₂ . R₄ 문제가 되는 구성 요소였습니다. (b) I₁에 대한 값 찾기 , 나₂ , 그리고 나₃ . (c) 5개의 저항 전류를 찾아 이전 값과 비교합니다.

해결책:

(a) 루트 I₃ R₅를 통해 , R_3, 및 R₁ 표시된 대로:

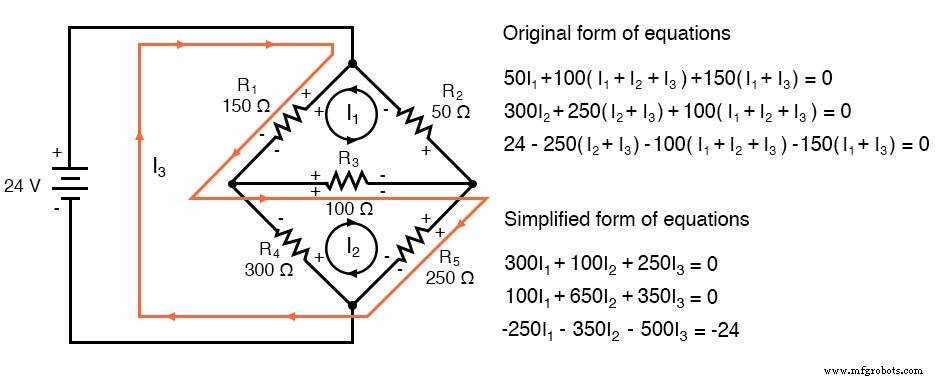
R₄의 극성이 상충한다는 점에 유의하십시오. 제거 되었어. 또한 다른 저항에는 극성이 충돌하지 않습니다.

(b) 오픈 소스(무료) Matlab 클론인 Octave는 "x"에서 메시 현재 벡터를 생성합니다.

<사전> 옥타브:1> A =[300,100,250;100,650,350;-250,-350,-500] A =300 100 250 100 650 350 -250 -350 -500 옥타브:2> b =[0;0;-24] b =0 0 -24 옥타브:3> x =A\b x =-0.093793 -0.058851 0.136092

모든 전류 I₁는 아닙니다. , 나₂ , 그리고 나₃ 동일합니다(I₂ ) 다른 루프 경로로 인해 이전 브리지로 그러나 저항 전류는 이전 값과 비교됩니다.

<사전> IR1 =I1 + I3 =-93.793ma + 136.092ma =42.299ma IR2 =I1 =-93.793ma IR3 =I1 + I2 + I3 =-93.793ma -58.851ma + 136.092ma =-16.552ma IR4 =I2 =-58.851mA IR5 =I2 + I3 =-58.851mA + 136.092mA =77.241mA

저항 전류는 이전 값과 동일하므로 저항 전압은 동일하므로 다시 계산할 필요가 없습니다.

검토:

<울>

"메시 전류" 분석 방법을 위해 따라야 할 단계:

(1) 회로의 루프에 모든 구성요소를 설명할 수 있을 정도로 메쉬 전류를 끌어옵니다.

(2) 메쉬 전류의 가정된 방향을 기반으로 저항 전압 강하 극성에 레이블을 지정합니다.

(3) 회로의 각 루프에 대한 KVL 방정식을 작성하고 방정식의 각 저항 항에서 E를 곱 IR로 대입합니다. 두 개의 메쉬 전류가 구성 요소를 통해 교차하는 경우 두 메쉬 전류의 대수적 합으로 전류를 표현합니다(즉, I₁ + 나₂ ) 전류가 해당 구성 요소를 통해 같은 방향으로 흐르는 경우. 그렇지 않은 경우 차이로 전류를 표현합니다(즉, I₁ - 나₂ ).

(4) 알 수 없는 메쉬 전류(동시 방정식)를 풉니다.

(5) 솔루션이 음수이면 가정된 현재 방향이 잘못된 것입니다!

(6) 여러 메쉬 전류를 공유하는 현재 구성 요소를 찾기 위해 메쉬 전류를 대수적으로 추가합니다.

(7) 모든 저항기(E=IR)에서 전압 강하를 해결합니다.

검사에 의한 메쉬 전류

모든 전류가 시계 방향(cw)으로 흐르는 "메시 전류 방법"을 다시 살펴봅니다. 동기는 저항 전압 강하 극성을 무시하여 메쉬 방정식 작성을 단순화하는 것입니다. 그러나 가정된 전류 방향과 관련하여 전압 소스의 극성에 주의를 기울여야 합니다. 저항 전압 강하의 부호는 고정된 패턴을 따릅니다.

저항 양단의 전압 강하 신호에 주의를 기울이는 아래 회로에 대한 기존의 메쉬 전류 방정식 세트를 작성하면 계수를 고정 패턴으로 재배열할 수 있습니다.

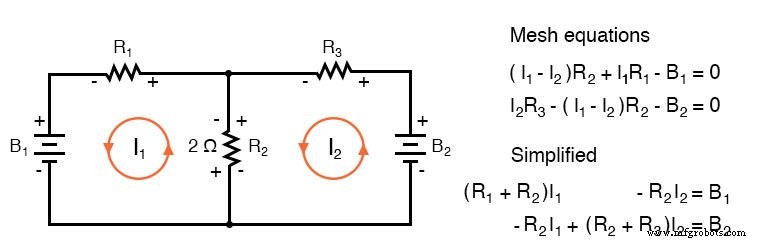
재배열되면 검사를 통해 방정식을 작성할 수 있습니다. 계수의 부호는 위의 쌍에서 고정된 패턴을 따르거나 아래 규칙에서 세 개의 집합을 따릅니다.

메시 현재 규칙:

<울>

이 방법은 기존의 전류 흐름 전압 소스를 가정합니다. 저항과 병렬로 연결된 전류원을 등가 저항과 직렬로 연결된 등가 전압원으로 교체합니다.

저항의 전류 방향 또는 전압 극성을 무시하고 모든 구성 요소를 가로지르는 시계 반대 방향 전류 루프를 그립니다. 중첩 루프를 피하세요.

알 수 없는 전류에 대한 전압 법칙 방정식 작성:I₁ , 나₂ , 그리고 나₃ . 방정식 1 계수 1, 방정식 2, 계수 2 및 방정식 3 계수 3은 각 루프 주변의 저항기의 양의 합입니다.

다른 모든 계수는 음수이며 한 쌍의 루프에 공통적인 저항을 나타냅니다. 방정식 1 계수 2는 루프 1과 2에 공통되는 저항이고 계수 3은 루프 1과 3에 공통되는 저항입니다. 다른 방정식과 계수에 대해서도 반복합니다.

+(R의 루프 1의 합)I1 - (공통 R 루프 1-2)I2 - (공통 R 루프 1-3)I3 =E1
-(공통 R 루프 1-2)I1 + ( R 루프 2)I2 - (공통 R 루프 2-3)I3 =E2
-(공통 R 루프 1-3)I1 - (공통 R 루프 2-3)I2 + (R 루프 3의 합 )I3 =E3

방정식의 오른쪽은 전자 전류 흐름 전압 소스와 같습니다. 시계 반대 방향으로 가정된 전류에 대한 전압 상승은 양수이고 전압 소스가 없는 경우 0입니다.

메시 전류에 대한 방정식 풀기:I₁ , 나₂ , 그리고 나3. KCL을 사용하여 개별 저항기를 통한 전류를 해결합니다. 옴의 법칙과 KVL을 사용하여 전압을 풉니다.

위의 규칙은 3개의 메쉬 회로에만 해당되지만 규칙은 더 작거나 더 큰 메쉬로 확장될 수 있습니다. 아래 그림은 규칙의 적용을 보여줍니다. 세 가지 전류는 모두 같은 방향인 시계 방향으로 흐릅니다. 세 개의 루프 각각에 대해 하나의 KVL 방정식이 작성됩니다. 저항에는 극성이 그려져 있지 않습니다. 계수의 부호를 결정하는 데 필요하지 않습니다. 우리는 전류 방향과 관련하여 전압 소스의 극성에 주의를 기울일 필요가 있습니다. 나₃ 시계 방향 전류는 l24V 소스의 (+) 양극 단자에서 흐른 다음 (-) 단자로 돌아갑니다. 이것은 기존의 전류 흐름에 대한 전압 상승입니다. 따라서 세 번째 방정식 오른쪽은 -24V입니다.

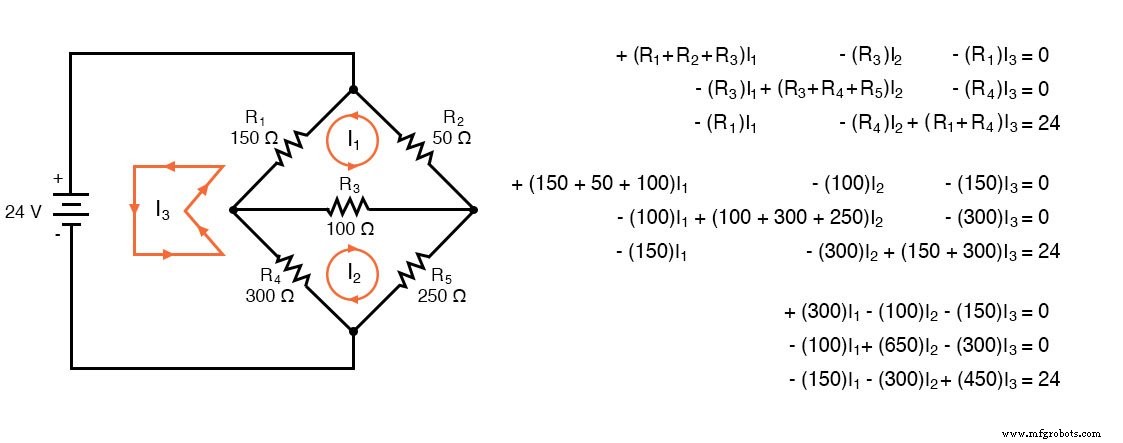
Octave에서 열 요소가 쉼표로 구분되고 행이 세미콜론으로 구분된 A 행렬에 계수를 입력합니다. 열 벡터에 전압을 입력합니다. b. 미지의 전류에 대해 풀기:I₁ , 나₂ , 그리고 나₃ 다음 명령으로:x=A\b. 이러한 전류는 x 열 벡터 내에 포함됩니다. 양수 값은 3개의 메쉬 전류가 모두 가정된 시계 방향으로 흐른다는 것을 나타냅니다.

<사전> 옥타브:2> A=[300,-100,-150;-100,650,-300;-150,-300,450] A =300 -100 -150 -100 650 -300 -150 -300 450 옥타브:3> b=[0;0;24] b =0 0 24 옥타브:4> x=A\b x =0.093793 0.077241 0.136092

메쉬 전류는 다른 메쉬 전류 방법으로 이전 솔루션과 일치합니다. 저항 전압 및 전류 계산은 이전 솔루션과 동일합니다. 여기에서 반복할 필요가 없습니다.

전기 공학 텍스트는 기존의 전류 흐름을 기반으로 합니다. 해당 텍스트의 루프 전류, 메쉬 전류 방법은 가정된 메쉬 전류를 시계 방향으로 실행합니다. . 기존의 전류는 회로를 통해 배터리의 (+) 단자에서 흘러 나와 (-) 단자로 돌아갑니다. 기존의 전류-전압 상승은 모든 전압 소스를 통해 (-)에서 (+)로 가정된 전류를 추적하는 것에 해당합니다.

이전 회로의 또 다른 예는 다음과 같습니다. 루프 1 주변의 저항은 6Ω, 루프 2 주변:3Ω입니다. 두 루프의 공통 저항은 2Ω입니다. I₁의 계수에 유의하십시오. 그리고 나₂ 방정식 쌍에서. B₁을 통해 가정된 시계 방향 루프 1 전류 추적 (+)에서 (-)까지 전자 전류 흐름 전압 상승에 해당합니다.

따라서 28V의 부호는 양수입니다. 루프 2는 B₂를 통해 (-)에서 (+)까지의 전류 추적을 시계 반대 방향으로 가정합니다. , 전압 강하. 따라서 B₂의 부호는 두 번째 메쉬 방정식에서 -7은 음수입니다. 다시 한번, 저항에 극성 표시가 없습니다. 방정식을 계산하지도 않습니다.

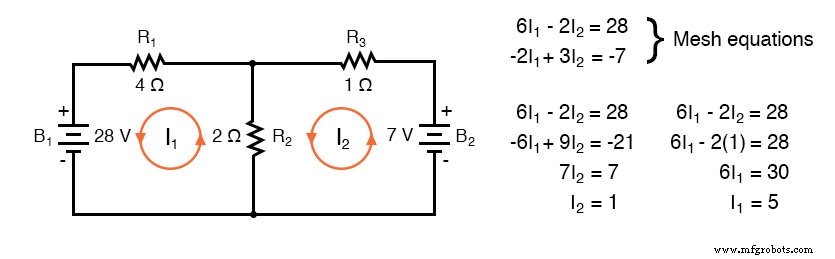
전류 I₁ =5A, I₂ =1 A는 모두 양수입니다. 둘 다 시계 방향 루프 방향으로 흐릅니다. 이는 이전 결과와 비교됩니다.

요약:

<울>

수정된 메쉬 전류 방법은 기존의 전류 흐름에 대해 모든 메쉬 전류를 시계 방향으로 그려 방정식 계수의 부호를 결정하지 않아도 됩니다.

그러나 루프에 있는 모든 전압 소스의 부호를 결정해야 합니다. 가정된 ccw 전류가 배터리(소스)와 함께 흐르는 경우 전압 소스는 양수입니다. 가정된 ccw 전류가 배터리에 흐를 경우 부호는 음수입니다.

자세한 내용은 위의 규칙을 참조하세요.

관련 워크시트:

<울>

DC 메시 전류 분석 워크시트