나노물질








원편광에 의해 유도된 역스핀 홀 효과는 GaAs/AlGaAs 2차원 전자 가스에서 관찰되었습니다. 스핀 횡력은 광유도 역스핀 홀 효과(PISHE) 전류를 이론적인 모델에 피팅하여 결정되었습니다. PISHE 전류는 또한 다른 광 전력과 다른 광점 프로파일에서 측정되며 모든 측정 결과는 이론적인 계산과 잘 일치합니다. 또한 다양한 온도(즉, 77~300K)에서 PISHE 전류를 측정합니다. PISHE 전류의 온도 의존성은 외부 메커니즘이 지배적인 역할을 한다는 것을 나타내며, 이는 샘플의 결정 방향에 대한 PISHE 전류의 약한 의존성에 의해 더욱 확인됩니다.
<섹션 데이터-제목="배경">Spintronics는 정보 기술에서의 잠재적인 응용과 응축 물질의 전자 스핀 물리학에 대한 근본적인 질문을 밝혀 많은 관심을 받았습니다[1-4]. 스핀 홀 효과(SHE)와 온사거 역의 역스핀 홀 효과(ISHE)는 스핀-궤도 결합을 통해 전하 전류를 스핀 전류로 또는 그 반대로 변환하는 전기적 방법을 제공하기 때문에 스핀트로닉스에서 중요한 역할을 합니다. SOC) [2, 5–8]. SHE 및 ISHE는 Pt, Ta, Py 및 IrMn과 같은 무거운 원소와 Bi2와 같은 새로운 위상 절연체를 포함하는 금속 필름에서 널리 연구되었습니다. Se3 및 SnT는 강력한 SOC로 인해 [9–14]. 이 두 가지 효과는 GaAs, ZnO, Si, Ge, GaN/AlGaN 및 GaAs/AlGaAs 2차원 전자 가스와 같은 반도체에서도 관찰됩니다[15-20].
반도체에서 스핀-전하 전류 변환은 스핀트로닉스와 전자공학을 통합하는 길을 열어주기 때문에 중요한 문제입니다[5]. 광유도 ISHE(PISHE)는 최근 반도체에서 ISHE를 조사하기 위한 효과적인 실험 도구로 떠오르고 있습니다. 이는 가우스 분포를 갖는 원형 편광을 이용하여 반도체에 스핀 전류를 도입한 다음 ISHE를 사용하여 충전 전류를 생성하는 것입니다. 2, 19–22]. PISHE 전류는 실온에서 관찰할 수 있으며 자기장 및 강자성 요소를 도입하지 않고 반도체의 ISHE를 조사하는 편리한 방법을 제공합니다[20]. 게다가, PISHE는 또한 새로운 종류의 스핀 광자 소자를 설계하는 길을 열어줍니다[22]. PISHE 전류는 GaN/AlGaN, GaAs/AlGaAs 및 MgZnO/ZnO 이종 구조에서 관찰되었습니다[2, 19, 20]. 그러나 광 전력 및 광 프로파일에 대한 PISHE 전류의 의존성은 여전히 알려져 있지 않습니다.
ISHE에는 두 가지 메커니즘, 즉 내재적 메커니즘과 외재적 메커니즘이 있습니다. 내재적 메커니즘은 Rashba[25-27] 또는 Dresselhaus SOC[26]에서 유래한 완전 질서 재료[7, 23, 24]의 밴드 구조에만 의존하는 반면, 외재적 메커니즘은 비대칭 Mott-skew 또는 측면을 나타냅니다. - 스핀-궤도 결합 시스템에서 불순물로 인한 점프 산란 [16, 24, 28, 29]. ISHE의 내적 또는 외적 기전에 대한 연구는 많이 있지만 이론적인 연구는 대부분이고 이 두 가지를 구별하는 것이 매우 어렵기 때문에 이에 초점을 맞춘 경험적 연구는 거의 없다[16, 27, 30-32]. 메커니즘을 실험적으로.
이 논문에서 우리는 GaAs/AlGaAs 2차원 전자 가스(2DEG)에서 PISHE 전류를 조사합니다. PISHE 전류는 온도가 증가함에 따라 증가하며, 이는 PISHE 전류가 주로 외부 메커니즘에 의해 지배됨을 나타냅니다. 이 추론은 샘플의 결정 방향에 대한 PISHE 전류의 약한 의존성에 의해 추가로 확인됩니다. 게다가, 우리는 또한 이론적인 모델과 매우 잘 일치하는 광 전력 및 광 프로파일에 대한 PISHE 전류의 의존성을 조사합니다.
실험은 반절연 GaAs 기판에서 분자빔 에피택시(MBE)에 의해 성장된 (001) 지향 변조 도핑된 GaAs/AlGaAs 2DEG 샘플에서 수행됩니다. 샘플의 전자 밀도 및 홀 이동도는 5.18 × 10 11 으로 측정되었습니다. cm −2 및 3.97 × 10 3 cm 2 V −1 s −1 실온에서 각각. 2DEG의 이동성은 10 15 정도의 배경 도핑으로 인해 약간 낮습니다. 또는 10 16 cm −3 , 샘플 성장 동안 도입된 샘플에서. 샘플은 [110] 및 \([1\bar {1}0]\) 방향을 따라 10 × 10mm의 정사각형으로 절단됩니다. 2 . [110] 및 [100] 방향을 따라 각각 8mm의 거리를 갖는 두 쌍의 옴 접촉은 인듐 증착에 의해 만들어지고 질소 분위기에서 약 420°C에서 어닐링됩니다.
1064 nm 파장의 다이오드 펌핑 고체 레이저가 방사선 소스로 사용됩니다. 레이저 빔은 초퍼, 편광판 및 1/4 파장판을 통과하여 최종적으로 샘플을 수직으로 비춥니다. 여기에서 편광자와 회전하는 1/4 파장판을 사용하여 빛의 나선도 P를 변경합니다. ㄷ =sin2φ 왼손잡이에서 (σ - , 피 ㄷ =− 1) 오른손잡이(σ) + , 피 ㄷ =+ 1) 연속적으로, 여기서 φ 는 입사광의 편광 방향과 1/4 파장판의 광축 사이의 각도입니다. 샘플의 광점에는 가우스 프로파일이 있습니다. 전류는 초퍼에서 기준 주파수가 229Hz인 전치 증폭기와 잠금 증폭기에 의해 샘플의 [100](또는 [110]) 방향을 따라 두 접점 사이에 수집됩니다. 그림 1a는 PISHE 전류를 측정하는 데 사용되는 설정을 보여줍니다.
<그림>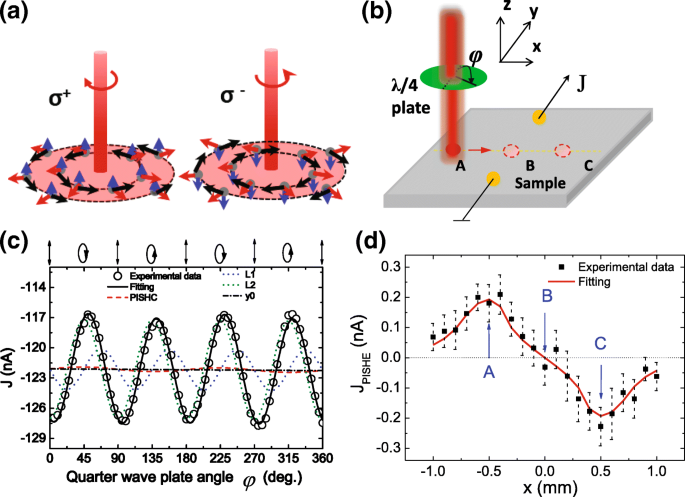
300K에서 측정된 PISHE 전류 및 PISHE를 얻는 방법. a 왼쪽 원형 편광(σ)의 일반 조명 아래에서 스핀 편광된 전자의 움직임에 대한 그림 + ) 또는 오른쪽 원형 편광(σ) - ) 빛. 빨간색 화살표는 전자의 흐름을 나타내고 파란색 화살표는 전자의 스핀 방향을 나타내며 검은색 화살표는 전자에 작용하는 스핀 횡력을 나타냅니다. ㄴ PISHE 전류를 측정하는 데 사용되는 형상입니다. ㄷ 위상각 φ의 함수로 300K에서 측정된 광전류 점 A에 광점이 표시될 때 수직 입사에서. 실선(검정색)은 Eq.를 사용한 피팅 곡선입니다. (1), 점선(빨간색)은 PISHE 전류를 나타내고 파란색 및 녹색 점선은 L을 나타냅니다. 1 그리고 L 2 요소. 점선은 배경 전류 J를 나타냅니다. 1 . d 300K에서 측정된 광점 위치의 함수로서의 PISHE 전류
전력 종속 측정의 경우 감쇠기를 사용하여 샘플에 조사되는 빛의 전력을 250mW에서 40mW로 변경합니다. 샘플의 광점 프로파일을 변경하기 위해 초점 거리가 다른 광학 렌즈가 채택되었습니다. 온도 의존적 측정에서 샘플은 광학 저온 유지 장치에 장착되어 77에서 300K까지의 온도 변화를 허용합니다.
Rashba 대 Dresselhaus SOC의 상대 비율을 얻기 위해 서로 다른 결정학적 방향에 대해 원형 광갈바닉 효과(CPGE)에 의해 유도된 광전류를 측정합니다. 즉, CPGE 전류는 접점을 통해 [110] 및 [100] 방향을 따라 각각 수집됩니다. 두 접점의 연결에 수직인 빛의 입사면이 있습니다. CPGE 측정의 경우 [110] 또는 [100] 방향을 따라 두 접점의 연결 중간점에서 빛이 비스듬히 조사되고 입사각 범위를 제외하고 PISHE 측정에서 사용된 것과 유사한 실험 설정이 채택되었습니다. - 40에서 40°까지. 특정 입사각에서의 CPGE 전류는 편광 상태 의존 광전류 J를 피팅하여 추출합니다. 다음 방정식 [33]에 대해 두 접점을 따라 수집됩니다. J =제 CPGE sin2φ +엘 11 sin4φ +엘 22 cos4φ +제 11 . 자, J CPGE 는 CPGE 전류, L 11 그리고 L 22 선형 편광에 의해 유도된 광전류 및 J 11 태양광 효과 또는 뎀버 효과[33]에서 발생하는 배경 전류입니다.
가우스 프로파일을 갖는 원형 편광의 조명 하에서, 공간에서 가우스 분포를 갖는 스핀 편광 캐리어가 흡수 불포화 영역에서 생성될 것입니다. 그 결과, 반경 방향을 따라 흐르는 확산 스핀 전류가 나타납니다. 그런 다음 ISHE 효과로 인해 스핀 극성 캐리어는 접선 방향을 따라 "스핀 가로 방향 힘"을 경험하여 축 방향으로 가로 전하 전류, 즉 와류 전류(PISHE 전류라고 함)를 발생시킵니다[8, 20], 도 1a에 도시된 바와 같이. 빛의 편광 상태가 왼쪽 원형 편광(σ + ) 오른쪽 원형 편광(σ) - ), 전자의 스핀 분극은 스핀 업에서 스핀 다운으로 변경되어 스핀 횡력과 PISHE 전류의 역전으로 이어집니다. 1/4 파장 플레이트가 0에서 180°로 회전할 때, 즉 각도 φ 0에서 180°로 변경하면 빛의 편광 상태가 수직선편광(0°에서)에서 왼쪽 원형편광(45°에서), 수직선편광(90°에서), 오른쪽으로 변경됩니다. 그림 1c의 상단과 같이 원형 편광(135°에서), 다시 수직 선형 편광(180°에서)을 차례로 수행합니다. 따라서 각도 φ 45°에서 135°로 변경되면 PISHE가 반전되어 PISHE가 sin2φ에 비례함을 나타냅니다. . φ에서 0, 90 및 180°의 각도에서 빛은 선형 편광됩니다. 선형 편광된 빛은 또한 L로 명명된 광학 운동량 정렬 효과[34]로 인해 광전류를 유도합니다. 1 , 또는 L로 명명된 이방성 광학 흡수로 인해 [35, 36] 2 . 전류 L 1 그리고 L 2 선형 편광에 의해 유도된 빛은 sin4φ에 비례합니다. 및 cos4φ , 각각. 게다가 배경 광전류 J 1 광기전력 효과 또는 뎀버 효과에서 비롯된 빛의 편광 상태와 무관한 뎀버 효과도 나타납니다. 따라서 각도 φ에 대한 서로 다른 의존성에 따라 , 우리는 실험적으로 측정된 편광 상태 의존 광전류 J를 피팅하여 PISHE 전류를 추출할 수 있습니다. 다음 공식으로 [8, 33]:
$$ J=J_{\text{PISHE}}\sin 2\varphi+L_{1}\sin 4\varphi+L_{2} \cos 4\varphi+J_{1}, $$ (1)여기서 J 피쉬 왼쪽 원형 편광에 의해 여기된 PISHE 전류, L 1 그리고 L 2 선형 편광에 의해 유도된 광전류 및 J 1 는 배경 전류[19]입니다. L 2 항이 피팅 방정식에 포함되었습니다. 즉, Eq. (1), 샘플에 존재하는 큰 광학 이방성으로 인해. 광학 이방성은 이방성 계면 구조[37], 원자 분리[38] 또는 잔류 응력[39]에 의해 유도될 수 있습니다.
PISHE의 공간 분포를 얻기 위해 수직 이등분선을 따라 두 접점의 왼쪽에서 오른쪽으로 레이저 스폿을 스윕합니다[그림 1a 참조]. 각 스폿 위치에서 1/4 파장 플레이트를 0에서 360°로 회전하고 Eq를 피팅하여 PISHE 전류를 얻습니다. (1) 실험적으로 측정된 편광 상태 의존 광전류 J . 그림 1b는 위상각 φ의 함수로 측정된 광전류의 일반적인 결과를 보여줍니다. , 레이저 스팟이 x에 고정된 경우 =− 0.5 mm, 즉, 점 A에서[그림 1a 참조]. 광전류는 300K에서 측정되고 [110] 방향을 따라 두 접점을 따라 수집됩니다. 샘플의 레이저 스폿은 직경이 약 1.4mm이고 가우스 프로파일이 있고 출력이 250mW입니다. 그림 1b의 원은 실험 데이터이고 실선은 Eq.에 따른 피팅 결과이다. (1). 실험적으로 측정된 광전류는 1/4 파장판을 회전시키면서 주기적으로 변동함을 알 수 있다. 이는 광전류가 PISHE 전류, 선형편광에 의해 유도된 광전류 및 배경전류의 합으로 각도 φ에 따라 다른 의존성을 보이기 때문이다. . 점선은 PISHE 전류를 나타내고 점선은 배경 전류를 나타냅니다. 파란색과 녹색 점선은 L을 나타냅니다. 1 그리고 L 2 선형 편광에 의해 유도된 성분. PISHE 전류가 선형 편광에 의해 유도된 광전류보다 훨씬 작은 것을 알 수 있습니다.
스폿의 함수로 얻은 PISHE 전류는 그림 1c에 나와 있습니다. 레이저 스폿이 두 접점의 왼쪽에서 오른쪽으로 이동함에 따라 PISHE 전류가 방향을 바꾸는 것을 볼 수 있습니다. 레이저 스폿이 두 접점의 중간점에 초점을 맞추면 PISHE 전류는 거의 0과 같습니다. 이 현상은 광유도 역스핀 홀 효과에 의해 유도된 와류 전류 모델에 의해 정량적으로 설명될 수 있다[20]. 특히, 가우스 프로파일 G를 가진 레이저의 방사 아래서 (r )=\(\frac {1}{\sqrt {2\pi }\sigma }\exp \left (-\frac {r^{2}}{2\sigma ^{2}}\right)\), 반경 방향을 따라 흐르는 스핀 전류가 유도되며, 이는 j로 표현될 수 있습니다. r =τ s 디 ∇r 지 (r ). 자, 디 스핀 확산 계수, τ s 스핀 이완 시간, r 반경 방향을 나타내고 σ 광도의 반치폭(FWHM)과 관련된 분포 편차를 나타냅니다. ISHE 효과로 인해, 스핀 편극 캐리어는 스핀 횡력 \(f(r)\propto j_{r}\times \hat {z}\) [20, 40]을 경험하게 되며, 이는 \( f(r)=-f_{0}r/\sigma ^{3}\exp \left (-\frac {r^{2}}{2\sigma ^{2}}\right)\). 여기서 f 0 는 재료 시스템의 SOC와 관련된 스핀 횡력 상수입니다. 소용돌이 전기장 \(\vec {E}\)은 원형 기전력(EMF)에 의해 결정될 수 있으며, \(\varepsilon (r_{0})=\frac {2\pi }{q }\int _{0}^{r_{0}} f(r)rdr\), \(\oint \vec {E}(r_{0})\cdot d\vec {l}=\varepsilon ( r_{0})\). 여기, r 0 는 광점의 반경이고 적분 루프는 광점의 둘레를 따라 있습니다. 따라서
$$ \nabla\times \vec{E}(r_{0})=-\frac{f_{0}r}{q\sigma^{3}}\exp \left(-\frac{r^{2 }}{2\sigma^{2}}\right). $$ (2)Eq.의 작은 차이는 주목할 가치가 있습니다. (2)와 [20]에서 보고된 것은 [20]에서는 정규화되지 않은 가우시안 함수를 본 논문에서는 정규화된 가우시안 함수를 사용했기 때문이다. f 0 이 문서에서 f와 동일합니다. 0 /σ [20]에 보고되었다. 두 접점 사이의 전류(a 그리고 b , 각각)는
로 표현될 수 있습니다. $$ {}I_{ab}\,=\,\frac{V_{ab}}{R_{ab}}\,=\,\frac{1}{R_{ab}}\!\int_{a} ^{b}\! \vec{E}\cdot d\vec{l}\,=\,\frac{1}{R_{ab}}\!\oint_{abo}\!\vec{E}\cdot d\vec{l }\,=\,\frac{1}{R_{ab}}\iint_{S}\nabla\times\vec{E} ds, $$ (3)여기서 V ab (R ab )는 접점 a 사이의 전압(저항)입니다. 그리고 b , 오 는 광점의 원점이며 S abo의 삼각형 영역을 나타냅니다. . 시료가 흡수하는 빛의 세기가 일정하고 시료의 최대흡수에 도달하는 흡수포화영역은 식의 적분에서 빼야 함을 언급해야 한다. (삼). 이는 광 발생 캐리어의 기울기가 해당 영역에서 0이고 결과적으로 해당 영역에서 스핀 전류와 PISHE 전류가 모두 0이기 때문입니다.
Eq. (3) 연락처 a 그리고 b 라이트 스폿 외부에 있기 때문에 라이트 스폿 Eq. (2)는 더 이상 유효하지 않습니다. 따라서 외부 전류(J f ) 및 내부(J e ) 스팟, 즉, J f =\(J_{e}\exp \left (-\frac {l}{A\cdot L_{s}}\right)\) [41], 우리는 Eq. (3) 다음과 같이
$$ I_{ab}=\frac{1}{R_{ab}}\iint_{D}\nabla\times\vec{E}\cdot\exp \left(-\frac{l}{A\cdot L_ {s}}\right)ds. $$ (4)여기, 나 광점의 가장자리와 두 접점의 연결 사이의 거리, L s 는 전자의 확산 길이이고 A 상수입니다. 식 사용하기 (2) 및 (4) 실험적으로 측정된 PISHE 전류에 맞추기 위해 스핀 횡력 f를 얻을 수 있습니다. 0 확산 길이 A ·엘 s . 피팅 결과는 그림 1c에 실선으로 표시되어 있습니다. 실험 데이터가 모델에 잘 맞는 것을 볼 수 있습니다. 피팅에서 다음과 같은 실험적으로 측정된 매개변수가 채택됩니다. σ =0.2mm, L =4mm, r 0 =0.7mm, R ab =15.5k Ω . 스핀 횡력 f 0 /q 전자의 수는 6.8 × 10 −6 에 맞춰집니다. N ·m/C at 300K, A ·엘 s 2.8 × 10 −4 에 맞춰집니다. m, 흡수 포화 영역의 반지름은 0.34mm로 맞춰졌으며, 이는 빛 I의 흡수 포화 강도를 나타냅니다. ㄷ 최대 강도 I의 약 1/5에 해당합니다. m , 즉, 나 ㄷ =1/5 나 m .
PISHE 전류가 광 전력 및 광 프로파일에 의존하는 것을 조사하기 위해 다른 광 파워 및 다른 광 프로파일에서 PISHE 측정을 수행합니다. 그림 2a, b는 광점 반경이 r인 다른 광 전력에서 광점 위치의 함수로 PISHE 전류를 보여줍니다. 0 =1.5mm 및 σ =0.5mm 및 r 0 =1mm 및 σ =각각 0.3mm. 기호는 실험 데이터이고 실선은 Eqs에 따른 이론적인 계산입니다. (2) 및 (4). 계산에서 광점 매개변수를 제외하고는 그림 1c에서 채택된 동일한 매개변수가 사용됩니다. 즉, f 0 /q =6.8 × 10 −6 N ·m/C, A ·엘 s =2.8 × 10 −4 m, R ab =15.5k Ω , 그리고 나 ㄷ =1/5 나 m . 여기, 나 m 는 전력이 250mW일 때 빛의 최대 광도입니다. PISHE 전류의 세기는 광 전력에 따라 증가하고 250mW의 전력 아래에서 FWHM이 더 큰 광점(즉, 더 큰 σ ) 더 큰 PISHE 전류로 이어집니다. 또한 FWHM이 더 큰 광점의 경우 PISHE 곡선의 피크가 x의 더 큰 값으로 표시됨을 알 수 있습니다. . 여기, x 광점 중심과 두 접점의 연결 중점 사이의 거리입니다. 이것은 스핀 전류와 결과적인 PISHE 전류가 광 프로파일의 기울기에 비례하기 때문입니다. 다른 광점 프로파일에 의해 유도된 PISHE 전류의 더 나은 비교를 위해 그림 2c의 그림 2a, b의 결과를 요약합니다. 즉, 다른 광점에 대한 여기 전력에 대한 PISHE 전류의 피크 값 의존성을 요약합니다 그림 2c의 광점 프로파일에서 기호는 실험 데이터를 나타내고 실선은 이론적인 계산 결과를 나타냅니다. 실험 결과가 이론적인 시뮬레이션과 매우 잘 일치하여 모델을 확인하는 것을 볼 수 있습니다.
<사진>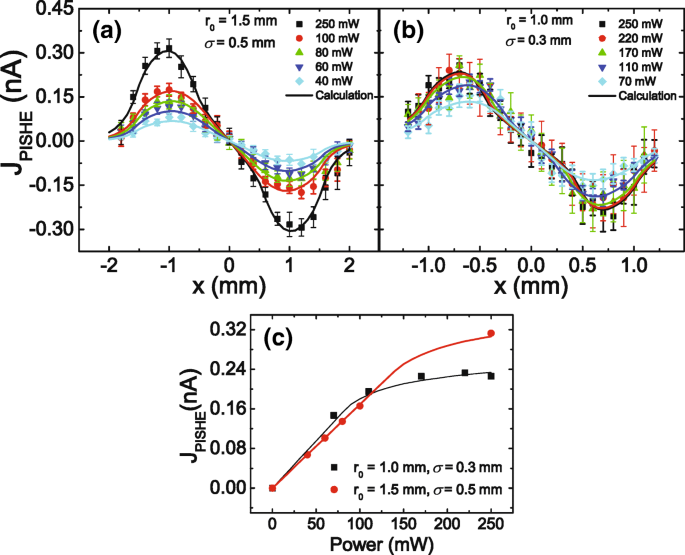
다른 광 전력 하에서 광점 위치의 함수로서의 PISHE 전류. 아 , b r이 있는 가우스 프로파일 광점에 의해 여기된 PISHE 전류 0 =1.5mm 및 σ =0.5mm 및 r 0 =1mm 및 σ =각각 0.3mm. ㄷ 여자 전력에 따른 PISHE 전류의 피크 값의 변화, 기호 및 실선은 각각 실험 데이터 및 이론 계산 결과입니다.
그림 2c는 전력이 증가함에 따라 PISHE 전류가 먼저 단조 증가하고 점차적으로 포화 상태가 됨을 나타냅니다. 광 전력으로 PISHE 전류의 포화가 나타나는 것은 고전력에서 흡수 포화가 존재하기 때문입니다. 최대 광도가 흡수 포화 강도보다 작을 때 PISHE 전류는 광 전력에 따라 선형적으로 증가합니다. 최대 광 강도가 흡수 포화 강도보다 클 때 PISHE 전류는 광 전력이 증가함에 따라 포화되는 경향이 있습니다. 광점의 크기가 PISHE 전류에 미치는 영향은 광점의 FWHM이 PISHE 전류에 미치는 영향 측면에서 이해할 수 있는데, 이는 광점의 크기와 FWHM이 광전력에 의해 상호 관련되기 때문이다. 구체적으로, 특정 광 파워에 대해 광반의 크기가 클수록 FWHM 값이 커집니다. 특정 광 전력에서 최대 광 강도가 흡수 포화 강도보다 작으면 FWHM이 작은 광 프로파일(즉, 광점의 크기가 작음)이 더 큰 PISHE 전류를 생성할 수 있습니다. 스핀 전류; 최대 광 강도가 흡수 포화 강도보다 크면 FWHM 값이 더 작은 광 프로파일은 더 작은 PISHE 전류로 이어집니다. 이것은 다른 광 프로파일에서 광점 위치의 함수로 PISHE 전류를 요약한 그림 3에서도 명확하게 볼 수 있습니다. 빛의 전력은 250mW입니다. σ의 값은 0.2에서 0.5mm로 증가하면 PISHE 전류의 피크 값이 단조롭게 감소합니다. 흡수포화영역에서는 스핀전류가 발생하지 않아 PISHE전류가 발생하지 않기 때문이다. 따라서 흡수 포화 영역 내부의 빛은 PISHE 전류에 기여하지 않습니다. 그림 3의 삽입은 다양한 가우시안 광 프로파일에 대한 광 강도 분포를 보여줍니다. 점선은 샘플의 흡수 포화 강도를 나타냅니다. 점선과 광도 곡선 사이의 교차점은 r으로 표시된 흡수 포화 영역의 반경을 나타냅니다. s . 반경 r의 원형 영역 내의 빛 s , r일 때 그림자 영역으로 표시됩니다. 0 =1.5 및 σ =0.5mm, PISHE 전류에 기여하지 않습니다. 250mW의 광 전력에 대해 더 작은 FWHM을 갖는 광 프로파일이 흡수 불포화 영역에서 더 큰 스핀 전류로 이어지지만 이 효과는 흡수 포화 영역에서 더 많은 에너지 낭비에 의해 압도된다는 것을 알 수 있습니다. 결과적으로 σ 값이 작은 광 프로파일 (즉, σ =0.2 mm) 더 큰 σ보다 작은 PISHE 값을 생성합니다. (즉, σ =0.3 또는 0.5mm).
<사진>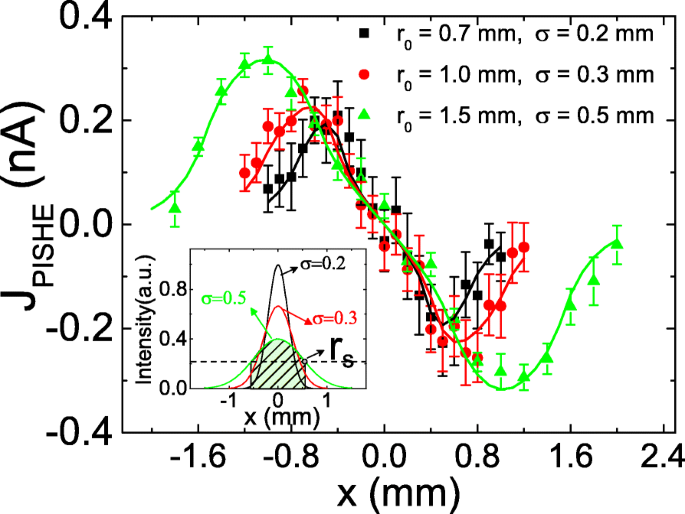
광 전력이 250mW일 때 다른 가우스 광 프로파일에서 광점 위치의 함수로서의 PISHE 전류. 삽입된 그림은 다양한 가우시안 광 프로파일에 대한 광도 분포를 보여줍니다. 점선은 샘플의 흡수 포화 강도를 나타냅니다.
PISHE의 지배적인 메커니즘을 조사하기 위해 다른 온도에서 PISHE 측정을 수행합니다. 그림 4a는 77, 130, 180 및 230K에서 측정된 광점 위치의 함수로 PISHE 전류를 보여줍니다. 레이저 점은 r 0 =0.7mm 및 σ =0.2mm이고 전력은 250mW입니다. 사각형은 실험 데이터를 나타내고 실선은 Eqs를 사용한 피팅 결과입니다. (2) 및 (4). 실험 데이터는 모든 온도에서 모델에 모두 잘 맞는 것을 볼 수 있습니다. 피팅에 의해 스핀 횡력 f를 얻을 수 있습니다. 0 /q , 그림 4b와 같이 전자의 확산 길이 A ·엘 s 다른 온도에서. 도 4b의 점선은 눈을 위한 가이드이다. 매개변수 A의 값을 결정하려면 , A의 온도 의존성을 비교해야 합니다. ·엘 s 전자 확산 길이 L의 온도 의존성에 대한 이전 결과 s . A의 가치에 맞춰 ·엘 s L 값으로 s [42]에서 얻은 상수 A 1.65 × 10 2 . 그림 4c에 표시된 이전 결과와 결과가 매우 잘 일치하면 방법이 검증됩니다. 전자 확산 길이는 온도가 증가함에 따라 감소한다는 것을 알 수 있으며, 이는 주로 포논에 의한 캐리어 산란의 향상에 기인할 수 있습니다[43].
<그림>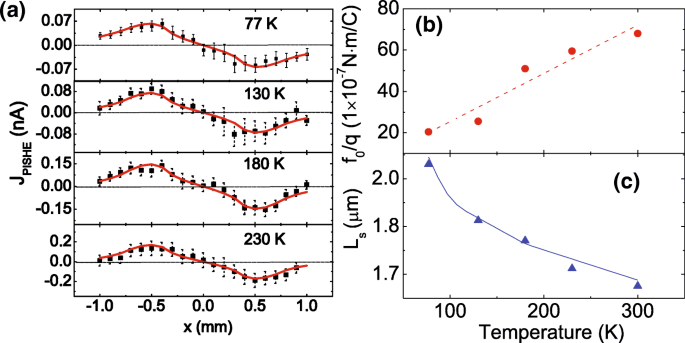
GaAs/AlGaAs 2DEG의 PISHE 전류, 스핀 횡력 및 전자 확산 길이의 온도 의존성. 아 다양한 온도에서 측정된 광점 위치의 함수로서 PISHE 전류의 실험 및 모델링 결과. 실선은 실험 데이터이고 실선은 피팅 결과입니다. ㄴ , ㄷ 스핀 횡력과 전자 확산 길이는 각각 온도의 함수입니다. b의 점선 는 눈의 안내선이고 c의 실선은 [42]
에서 얻습니다.놀랍게도, 스핀 횡력 f 0 /q Au/InP 하이브리드 구조에서 관찰된 PISHE에 대한 온도의 반대 변화 경향을 나타내는 2DEG의 2DEG는 온도가 증가함에 따라 단조롭게 증가합니다[44]. 이 예상치 못한 현상은 PISHE의 메커니즘과 관련이 있을 수 있습니다. 반도체 2DEG에서 PISHE에 대한 두 가지 메커니즘, 즉 고유 및 외부 메커니즘이 있습니다. 전자는 주로 밴드 구조에서 발생하고 후자는 불순물의 SOC 효과로 인한 상하 스핀 산란의 비대칭에서 발생한다[7, 16]. C의 반도체 2DEG의 경우 2v 점군 대칭, 고유 메커니즘에 의해 유도된 스핀 횡력은 \(f_{0}=\frac {4m^{*2}\tau _{s}D}{\hbar ^{2}}\left로 표현될 수 있습니다. (\alpha ^{2}+\beta ^{2}\right)\) [20, 40], 여기서 \(\hbar \)는 축소된 플랑크 상수, τ s 스핀 이완 시간, D 는 스핀 확산 계수이고 α (또는 β )은 Rashba(또는 Dresselhaus) SOC의 강도에 비례하는 Rashba(또는 Dresselhaus) 상수입니다. GaAs/AlGaAs 2DEG의 경우 스핀 완화 시간 τ s T에 비례합니다. −1 [45]. 여기, T 온도를 나타냅니다. 변조 도핑된 2DEG의 경우 Rashba SOC의 강도는 Dresselhaus의 강도보다 훨씬 큽니다(다음 논의 참조). 결과적으로 Rashba 상수 α Dresselhaus 상수 β보다 훨씬 큽니다. . 스핀 확산 계수 D T에 비례합니다. −2 [46, 47]. α의 온도 의존성 a로 표현할 수 있습니다. +ㄴ 티 , 여기서 a 그리고 b 상수이고 a b보다 약 두 주문이 큽니다. [48]. 따라서 τ의 온도 의존성을 고려하면 s , 디 , 및 α , 우리는 f 0 ∝티 −3 이는 고유 메커니즘에 의해 유도된 스핀 횡력이 온도가 증가함에 따라 감소해야 함을 시사합니다. 외부 메커니즘의 경우 스핀 가로 방향 힘은 특히 외부 측면 점프 산란의 경우 이온화된 불순물의 농도에 따라 달라집니다[49, 50]. 샘플에 배경 도핑이 있고 온도가 증가함에 따라 불순물 이온화가 증가하기 때문에 스핀업 및 스핀다운 전자에 대한 더 강한 비대칭 산란이 온도가 증가함에 따라 발생하여 온도가 증가함에 따라 더 큰 스핀 횡력을 유발합니다. 스핀 횡력 <>f 0 우리 실험에서 관찰된 온도가 증가함에 따라 증가하는 것을 볼 때, PISHE는 성장 과정에서 백그라운드 도핑에 의해 주로 불순물이 도입되는 외부 메커니즘에 의해 지배됨을 유추할 수 있습니다.
PISHE가 실제로 외부 메커니즘에 의해 지배된다는 것을 추가로 확인하기 위해 다른 결정 방향을 따라 수집된 PISHE 전류의 공간 분포를 측정합니다. 그림 5a, b는 각각 [110] 및 [100] 결정 방향을 따라 수집된 PISHE 전류의 공간 분포를 보여줍니다. 서로 다른 결정 방향에서 캐리어 이동도와 캐리어 밀도의 영향을 제거하기 위해 해당 광전류 J로 PISHE 전류를 정규화합니다. 0 접점이 각각 [110] 및 [100] 방향을 따라 있을 때 0.3V의 바이어스에서. 측정은 60mW의 전력을 방출하는 실온에서 수행됩니다. 광점 반경 r 0 는 1.0mm이고 σ 0.3mm입니다. 기호는 실험 데이터를 나타내고 실선은 Eqs에 따른 피팅 결과입니다. (2) 및 (4). [110] 및 [100] 결정 방향을 따라 수집된 정규화된 PISHE 전류 사이에 뚜렷한 차이가 없음을 알 수 있습니다.
<그림>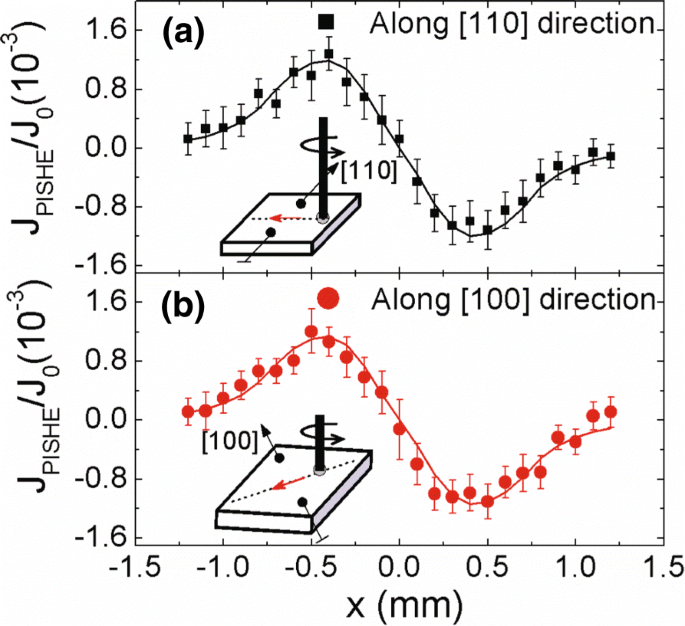
다른 결정 방향을 따라 수집된 정규화된 PISHE 전류. PISHE 전류는 0.3V의 바이어스에서 광전류로 정규화됩니다. 실선은 실험 데이터이고 실선은 이론적인 피팅 결과입니다. 삽입은 해당 측정 형상에 대한 개략도를 보여줍니다.
고유 메커니즘의 경우 특정 결정 방향을 따른 PISHE 전류는 해당 방향에서의 스핀 분할과 관련이 있습니다. GaAs/AlGaAs 2DEG에서 이방성 스핀 분할에 대한 지식을 얻기 위해 실온에서 CPGE 전류의 결정 방향 의존성을 측정합니다. 즉, 두 접점이 [110](또는 [100 ]) 방향이고 빛의 입사면은 [1\(\bar{1}\)0](또는 [010]) 방향이며, 측정 결과는 그림 6에서 정사각형(또는 원)으로 표시됩니다. . It is worth mentioning that when measuring the CPGE current, the light spot is located at the midpoint of the connection of the two contacts, where the PISHE is zero according to [20]. The CPGE current is also normalized by the corresponding photocurrent under a bias of 0.3 V to eliminate the influence of the carrier mobility and the carrier density in different crystal directions [51]. Then, we use the following equation to fit the normalized angle-dependent CPGE current to obtain the relative SOC strength along different crystal directions [21, 27]:
$$ \begin{aligned} J^{\lambda}/J_{0}=\frac{A_{\lambda}\sin \theta \cos^{2} \theta}{n\left[\cos\theta+\left(n^{2}-\sin^{2} \theta\right)^{1/2}\right]\left[n^{2}\cos \theta +\left(n^{2}-\sin^{2}\theta\right)^{1/2}\right]}. \end{aligned} $$ (5)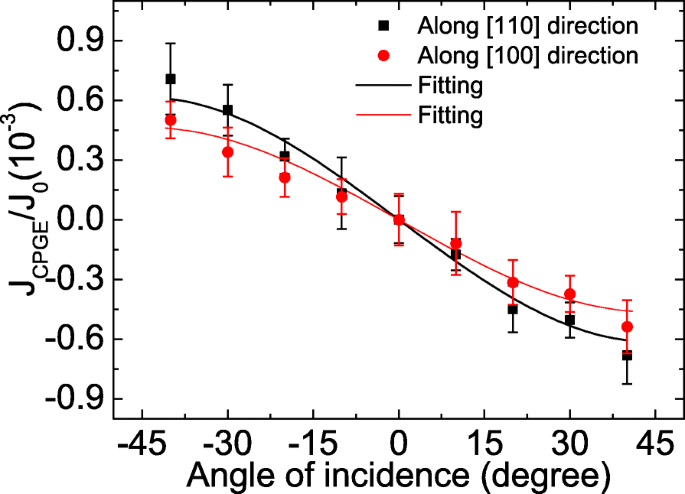
Incident angle dependence of the normalized CPGE current collected along different crystal orientations. The CPGE current is normalized by the photocurrent under a bias of 0.3 V. The solid symbols are the experimental data, and the lines are the fitting results according to Eq. (5)
여기, θ is the angle of incidence, n is the refractive index of GaAs, and A λ is a constant proportional to the SOC constant. The fitting results are shown by the solid lines in Fig. 6. When the incident plane of light lies in [1\(\bar {1}\)0] direction and the CPGE current is collected along [110] direction, the corresponding A parameter, denoted as A [110] , is proportional to the sum of Rashba and Dresselhaus SOC, i.e., A [110] ∝α +β [51–53]. When the incident plane of light lies in [010] direction and the CPGE current is collected along [100] direction, the corresponding A parameter, denoted as A [100] , is proportional to the Rashba SOC, i.e., A [100] ∝α [51–53]. Thus, by the ratio of A [110] /A [100] , we can get the relative ratio of Rashba to Dresselhaus SOC, i.e., \(\beta /\alpha =\frac {A_{[110]}}{A_{[100]}}-1\) =0.32, which indicates that the spin splitting in the GaAs/AlGaAs 2DEG has crystal anisotropy [21]. Therefore, the intrinsic contribution to the PISHE should be sensitive to the crystal axis [16]. Specifically speaking, according to Eqs. (2) and (4), when the contacts are along [110] (or [100]) direction, the measured PISHE current is dominated by the inverse spin Hall current flowing nearly parallel to [110] (or [100]) direction since the PISHE current is a vortex current. If the intrinsic mechanism plays a dominant role in the 2DEG, the PISHE current collected along these two directions should be different. However, no marked difference is observed, which suggests that the extrinsic mechanism is dominant in the GaAs/AlGaAs 2DEG.
In conclusion, the PISHE current in a GaAs/AlGaAs 2DEG has been investigated in a temperature range of 77 to 300 K. The spin transverse force has been determined by fitting the PISHE current to a theoretical model. The dependence of the PISHE on the light power and on the light spot profiles has been investigated, which shows a good agreement with the theoretical model. The evolution of the PISHE current with temperature suggests that the PISHE is dominated by the extrinsic mechanism, which is further confirmed by the weak dependence of the PISHE current on the crystal orientation of the sample.
Two-dimensional electron gas
Circular photogalvanic effect
Circular electromotive force
최대 절반에서 전체 너비
Inverse spin Hall effect
분자빔 에피택시
Photo-induced inverse spin Hall effect
Spin Hall effect
Spin-orbit coupling
나노물질
문제가 기계 시스템의 속도, 변위 또는 근접성과 같은 변수를 감지했습니까? 아니면 프로젝트에 물체의 위치나 자기장의 존재를 감지하기 위한 무언가가 필요합니까? 우리가 답을 가지고 있기 때문에 당신은 운이 좋습니다. 홀 효과 센서만 있으면 됩니다. 이 센서는 자극의 극성을 식별하고 자기장의 강도를 측정하는 등 다양한 용도로 사용됩니다. 따라서 이 기사에서는 홀 효과 센서에 대한 모든 것을 설명하고 Arduino를 사용하여 간단한 홀 효과 회로를 구축하는 방법을 보여줍니다. 시작하겠습니다. 자기 홀 효과 센서란 무엇입니까? 자
커피 머신이나 수도관의 유량을 구하려는 시나리오를 생각해 보십시오. 이러한 측정은 유량 펄스 센서가 있어야 가능합니다. 오늘, 우리는 YF-S201 유량 센서의 작동과 그 응용에 대해 자세히 설명할 것입니다. YF-S201이란 무엇입니까? 그림 1:유량 측정 센서 홀 효과 센서, 워터 로터 및 플라스틱 바디 밸브로 구성된 유량 측정 센서입니다. 분당 리터를 결정하기 위해 물 흐름 센서 YF-S201은 홀 센서의 펄스 출력을 기록합니다. 평균적으로 펄스는 2.25밀리리터이지만 이 장치는 정밀 센서가 아닙니다. 따라서 정