10진수에서 변환

8진법 및 16진법 계산 시스템은 2진법(2진법)의 배수인 기수가 있기 때문에 16진법 또는 8진법과 이진법 간의 변환이 매우 쉽습니다.

또한 우리는 10진법에 매우 익숙하기 때문에 2진법, 8진법 또는 16진법을 10진 형식으로 변환하는 것은 비교적 쉽습니다(단순히 암호 값과 자릿수를 더하면 됩니다).

그러나 십진수에서 이러한 "이상한" 숫자 체계로의 변환은 다른 문제입니다.

시험 및 맞춤 방법

아마도 가장 의미가 있는 방법은 2진법, 8진법 또는 16진법 표기법을 10진수 형식으로 표시된 원하는 값에 "맞추려고" 시도하는 "시행적합" 방법입니다.

예를 들어 87이라는 10진수 값을 이진 형식으로 표현하고 싶다고 가정해 보겠습니다. 자릿수 값으로 완성된 이진수 필드를 그리는 것으로 시작하겠습니다.

글쎄, 우리는 128의 자리에 "1" 비트가 없을 것이라는 것을 알고 있습니다. 왜냐하면 그것은 즉시 87보다 큰 값을 줄 것이기 때문입니다.

그러나 오른쪽(64)의 다음 가중치가 87보다 작기 때문에 거기에 "1"이 있어야 함을 압니다.

오른쪽에 있는 다음 자리도 "1"로 하면 총 값은 64₁₀이 됩니다. + 32₁₀ , 또는 96₁₀ . 87₁₀보다 큽니다. , 그래서 우리는 이 비트가 "0"이어야 한다는 것을 압니다.

다음(16) 자리 비트를 "1"과 같게 하면 총 값이 64₁₀가 됩니다. + 16₁₀ , 또는 80₁₀ , 우리가 원하는 값에 더 가깝습니다(87₁₀ ) 초과하지 않음:

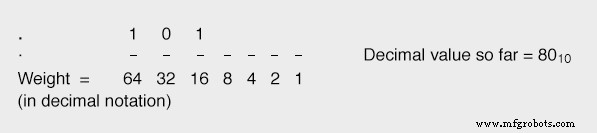
이 진행을 계속하면서 원하는 총 값을 초과하지 않고 도달할 필요가 있을 때마다 더 적은 가중치를 설정하면 결국 올바른 수치에 도달하게 됩니다.

8진법과 16진법의 시행착오

이 시행착오 전략은 8진수 및 16진수 변환에서도 작동합니다. 같은 십진수 87₁₀을 보겠습니다. , 8진수로 변환:

64 자리에 "1"이라는 암호를 넣으면 총 값은 64₁₀가 됩니다. (87₁₀ 미만 ). 64 자리에 "2"라는 암호를 넣으면 총 값은 128₁₀이 됩니다. (87₁₀ 초과 ). 이것은 8진수 숫자가 64 자리에서 "1"로 시작해야 함을 알려줍니다.

이제 8의 자리에 있는 암호 값을 실험하여 총(십진수) 값을 초과하지 않고 가능한 한 87에 가까운 값을 얻으려고 시도해야 합니다. 처음 몇 가지 암호 옵션을 시도하면 다음을 얻습니다.

8 자리에 암호 값이 "3"이면 원하는 합계인 87₁₀을 초과하게 됩니다. , 그래서 "2"입니다!

물론, 8진/2진 변환에 대한 마지막 섹션에서 주의를 기울였다면 (십진) 87₁₀의 이진 표현을 사용할 수 있다는 것을 알게 될 것입니다. , 우리는 이전에 1010111₂로 결정했습니다. , 그리고 그것을 8진수로 쉽게 변환하여 우리의 작업을 확인하십시오:

같은 방식으로 10진수에서 16진수로 변환할 수 있습니까? 물론이죠. 하지만 누가 원하겠습니까? 이 방법은 이해하기 쉽지만 수행하기가 어렵습니다.

이러한 변환을 수행하는 또 다른 방법이 있습니다. 이 방법은 본질적으로(수학적으로) 동일하지만 수행하기가 더 쉽습니다.

반복 나눗셈 기법

이 다른 방법은 10진수 표기법을 사용하여 반복되는 나누기 주기를 사용하여 10진수 숫자를 2진수, 8진수 또는 16진수 자리 가중치 값의 배수로 나눕니다.

나눗셈의 첫 번째 주기에서 우리는 원래의 10진수를 가져와 우리가 변환할 수 체계의 밑수로 나눕니다(2진수=2 8진수=8, 16진수=16).

그런 다음 나누기 결과(몫)의 정수 부분을 다시 기본 값으로 나누는 식으로 몫이 1보다 작아질 때까지 계속합니다.

2진수, 8진수 또는 16진수는 각 나눗셈 단계에서 남은 "나머지"에 의해 결정됩니다. 87₁₀의 십진법 예제를 사용하여 이진법이 어떻게 작동하는지 봅시다. :

이진 비트는 LSB에서 시작하여 MSB로 이어지는 연속 분할 단계의 나머지 부분에서 조합됩니다. 이 경우 1010111₂의 이진 표기법에 도달합니다. .

우리가 2로 나눌 때, 우리는 항상 ".0" 또는 ".5"로 끝나는 몫, 즉 0 또는 1의 나머지를 얻게 될 것입니다. 이전에 말했듯이, 변환을 위한 이 반복 나누기 기술은 계산에 사용할 것입니다. 바이너리가 아닌 시스템.

8진수로의 변환을 위해 8과 같이 다른 숫자를 사용하여 연속적인 나눗셈을 수행한다면 필연적으로 0과 7 사이의 나머지를 얻게 될 것입니다. 동일한 10진수 87₁₀로 시도해 보겠습니다. :

1보다 작은 수량을 다루는 숫자 체계를 변환하는 데에도 유사한 기술을 사용할 수 있습니다.

1보다 작은 10진수를 2진수, 8진수 또는 16진수로 변환하기 위해 반복 곱셈을 사용하여 각 단계에서 곱의 정수 부분을 변환된 숫자의 다음 자릿수로 취합니다.

십진수 0.8125₁₀를 사용하겠습니다. 예를 들어 바이너리로 변환:

정수에 대한 반복 나누기 프로세스와 마찬가지로 각 단계는 "포인트"에서 더 멀리 떨어진 다음 숫자(또는 비트)를 제공합니다.

정수(나누기)의 경우 LSB에서 MSB(오른쪽에서 왼쪽)로 작업했지만 곱셈을 반복하면 왼쪽에서 오른쪽으로 작업했습니다.

1보다 큰 10진수를 <1 구성요소로 변환하려면 둘 다 사용해야 합니다. 한 번에 하나씩 기술. 54.40625₁₀의 십진법을 예로 들어 보겠습니다. , 바이너리로 변환:

관련 워크시트:

<울>

숫자 체계 워크시트