구형파 신호

모든 반복되는 비사인파 파형은 다양한 진폭과 주파수에서 DC 전압, 사인파 및/또는 코사인파(90도 위상 편이가 있는 사인파)의 조합과 동일할 수 있습니다.

문제의 파형이 아무리 이상하거나 복잡하더라도 이것은 사실입니다. 시간이 지남에 따라 규칙적으로 반복되는 한 이 일련의 사인파로 축소될 수 있습니다.

특히, 구형파는 동일한 주파수에서 사인파의 합과 진폭이 감소하는 무한한 시리즈의 홀수 다중 주파수 사인파의 합과 수학적으로 동일하다는 것이 밝혀졌습니다.

파형에 대한 이 진실은 처음에는 믿기에 너무 이상해 보일 수 있습니다. 그러나 구형파가 실제로 함께 추가된 무한한 일련의 사인파 고조파라면 구형파에 가까운 근사치를 생성하기 위해 여러 사인파 고조파를 함께 ​​추가하여 이를 증명할 수 있어야 합니다.

이 추론은 건전할 뿐만 아니라 SPICE로 쉽게 입증됩니다.

우리가 시뮬레이션할 회로는 직렬로 함께 연결된 적절한 진폭과 주파수의 여러 사인파 AC 전압 소스에 불과합니다. SPICE를 사용하여 다음과 같이 전압 소스를 연속적으로 추가하는 동안 전압 파형을 플로팅합니다.

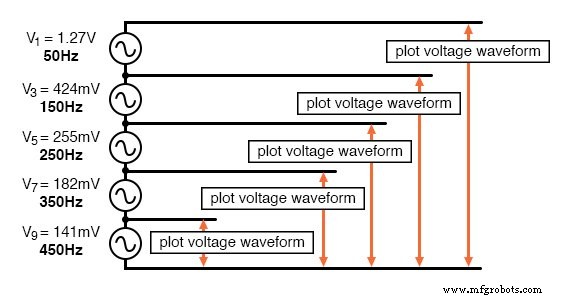
구형파는 고조파의 합으로 근사됩니다.

이 특정 SPICE 시뮬레이션에서 총 5개의 AC 전압 소스에 대해 직렬로 1차, 3차, 5차, 7차 및 9차 고조파 전압 소스를 합산했습니다. 기본 주파수는 50Hz이고 각 고조파는 물론 해당 주파수의 정수배입니다.

진폭(전압) 수치는 난수가 아닙니다. 오히려, 주파수 시리즈(증가하는 홀수 고조파 각각에 대해 1, 1/3, 1/5, 1/7 등을 곱한 분수 4/π)에 표시된 방정식을 통해 도달했습니다.

<사전>구형파 만들기 v1 1 0 sin(0 1.27324 50 0 0) 1차 고조파(50Hz) v3 2 1 sin (0 424.413m 150 0 0) 3차 고조파 v5 3 2 sin (0 254.648m 250 0 0) 5차 고조파 v7 4 3 sin (0 181.891m 350 0 0) 7차 고조파 v9 5 4 sin (0 141.471m 450 0 0) 9차 고조파 r1 5 0 10k .트란 1m 20m .plot tran v(1,0) 1차 고조파 플롯 .plot tran v(2,0) 플롯 1차 + 3차 고조파 .plot tran v(3,0) 플롯 1차 + 3차 + 5차 고조파 .plot tran v(4,0) 플롯 1차 + 3차 + 5차 + 7차 고조파 .plot tran v(5,0) 플롯 1st + . . . + 9차 고조파 .끝

여기에서 단계적으로 분석 단계를 설명하고 우리가 보고 있는 것이 무엇인지 설명합니다. 이 첫 번째 플롯에서 50Hz의 기본 주파수 사인파 자체를 볼 수 있습니다. 추가적인 고조파 성분이 없는 순수한 사인 형태일 뿐입니다. 이것은 이상적인 AC 전원에서 생성되는 파형의 종류입니다.

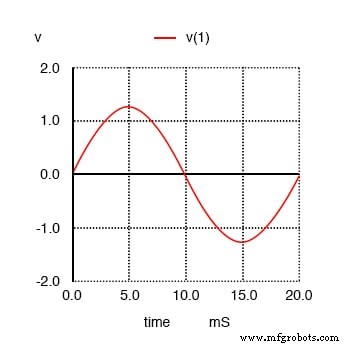
순수한 50Hz 사인파.

다음으로 이 깨끗하고 단순한 파형이 3차 고조파(50Hz 또는 150Hz의 3배)와 결합될 때 어떤 일이 발생하는지 봅니다. 갑자기 더 이상 깨끗한 사인파처럼 보이지 않습니다.

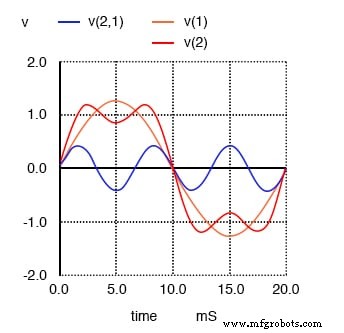
1차(50Hz) 및 3차(150Hz) 고조파의 합은 50Hz 구형파에 가깝습니다.

포지티브 사이클과 네거티브 사이클 사이의 상승 및 하강 시간은 이제 훨씬 더 가파르고 파동의 마루는 구형파처럼 평평해집니다. 다음 홀수 고조파 주파수를 추가할 때 어떤 일이 발생하는지 살펴보세요.

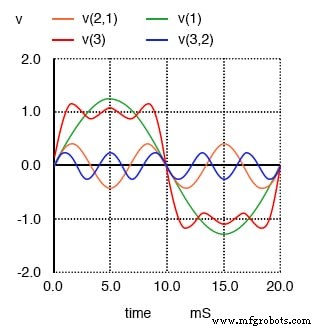
1차, 3차, 5차 고조파의 합은 구형파에 가깝습니다.

여기서 가장 눈에 띄는 변화는 파도의 마루가 훨씬 더 평평해진 것입니다. 파도의 양쪽 끝에 더 많은 딥과 마루가 있지만 이러한 딥과 마루는 이전보다 진폭이 더 작습니다. 다음 홀수 고조파 파형을 믹스에 추가할 때 다시 시청하십시오.

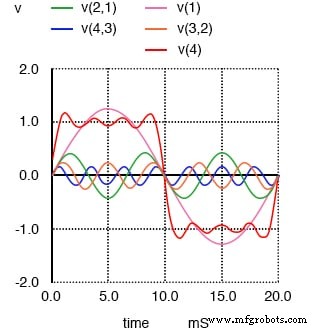
1차, 3차, 5차, 7차 고조파의 합은 구형파에 가깝습니다.

여기서 우리는 각 피크에서 파도가 더 평평해지는 것을 볼 수 있습니다. 마지막으로 회로에 5번째 사인파 전압 소스인 9번째 고조파를 추가하면 다음과 같은 결과를 얻을 수 있습니다.

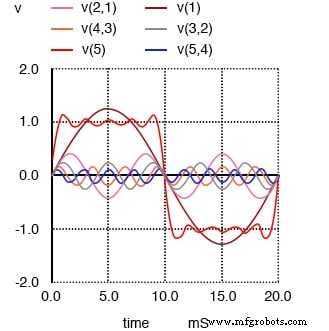
1차, 3차, 5차, 7차 및 9차 고조파의 합은 구형파에 가깝습니다.

처음 5개의 홀수 고조파 파형을 함께 추가한 최종 결과(물론 모두 적절한 진폭에서)는 구형파에 가까운 근사치입니다. 이 작업의 요점은 순수한 구형파가 실제로 시리즈와 동일하다는 것을 증명하기 위해 서로 다른 주파수의 여러 사인파에서 구형파를 생성하는 방법을 설명하는 것입니다. 사인파.

구형파 AC 전압이 무효 부품(커패시터 및 인덕터)이 있는 회로에 적용되면 해당 부품은 실제로 서로 다른 주파수의 여러 사인파 전압에 노출되는 것처럼 반응합니다.

반복되는 비정현파가 일련의 추가 DC 전압, 사인파 및/또는 코사인파와 동일하다는 사실은 파동이 작동하는 방식의 결과입니다. 즉, 전기적 또는 기타 모든 파동 관련 현상의 기본 속성입니다.

비정현파를 이러한 구성 주파수로 줄이는 수학적 과정을 푸리에 분석이라고 합니다. , 자세한 내용은 이 텍스트의 범위를 훨씬 벗어납니다. 그러나 컴퓨터 알고리즘은 실제 파형에 대해 고속으로 이 분석을 수행하기 위해 만들어졌으며 AC 전력 품질 및 신호 분석에 널리 적용됩니다.

SPICE에는 파형을 샘플링하고 푸리에 변환을 통해 구성 사인파 고조파로 줄이는 기능이 있습니다. 알고리즘을 사용하여 주파수 분석을 숫자 테이블로 출력합니다. 홀수 고조파 사인파로 구성되어 있다는 것을 이미 알고 있는 구형파에 대해 시도해 보겠습니다.

구형파 분석 넷리스트 v1 1 0 펄스(-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .트란 1m 40m .plot tran v(1,0) .4 50 v(1,0) .끝 

펄스 전압 소스 v1를 설명하는 넷리스트 라인의 옵션 SPICE가 정사각형 모양의 "펄스" 파형을 시뮬레이션하도록 지시합니다. 이 경우 대칭(각 반주기에 대해 동일한 시간)이고 피크 진폭이 1볼트입니다. 먼저 분석할 구형파를 플로팅합니다.

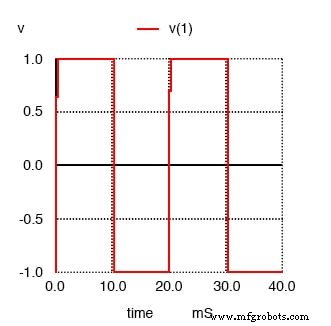
SPICE 푸리에 분석을 위한 Squarewave

다음으로 이 구형파에 대해 SPICE에서 생성한 푸리에 분석을 인쇄합니다.

<사전>과도 응답 v(1)의 4가지 구성 요소 DC 구성 요소 =-2.439E-02 고조파 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 5.000E+01 1.274E+00 1.000000 -2.195 0.000 2 1.000E+02 4.892E-02 0.038415 -94.390 -92.195 3 1.500E+02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E+02 4.936E-02 0.038757 -98.780 -96.585 5 2.500E+02 2.562E-01 0.201179 -10.976 -8.780 6 3.000E+02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E+02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E+02 5.116E-02 0.040175 -107.561 -105.366 9 4.500E+02 1.443E-01 0.113316 -19.756 -17.561 총 고조파 왜곡 =43.805747%

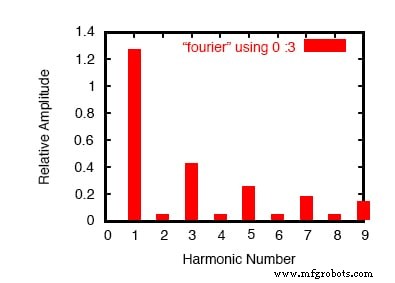
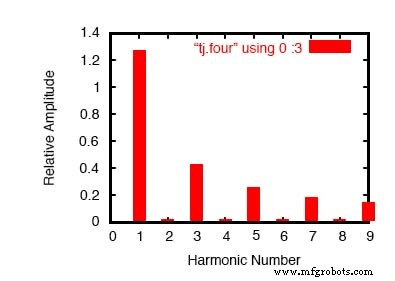
푸리에 분석 결과 플롯

여기(위 그림)에서 SPICE는 파형을 최대 9차 고조파까지의 사인파 주파수 스펙트럼과 DC 구성 요소라고 표시된 작은 DC 전압으로 분류했습니다. .

SPICE에 기본 주파수(주기가 20ms인 구형파의 경우 이 주파수는 50Hz)를 알려야 하므로 고조파 분류 방법을 알고 있었습니다. 모든 짝수 고조파(2차, 4차, 6차, 8차)에 대한 수치가 얼마나 작은지, 홀수 고조파의 진폭이 얼마나 감소하는지(1차 고조파가 가장 크고 9차가 가장 작음) 유의하십시오.

이와 동일한 "푸리에 변환" 기술은 AC 파형을 샘플링하고 고조파 함량을 결정하는 컴퓨터 전력 계측에 자주 사용됩니다. 이를 위한 일반적인 컴퓨터 알고리즘(작업을 수행하기 위한 프로그램 단계의 순서)은 고속 푸리에 변환입니다. 또는 FFT 기능.

이러한 컴퓨터 루틴이 정확히 어떻게 작동하는지 걱정할 필요는 없지만 그 존재와 적용을 알고 있어야 합니다.

SPICE에서 파동의 고조파 성분을 분석하는 데 사용되는 동일한 수학적 기술은 음악의 기술적 분석에 적용될 수 있습니다. 즉, 특정 사운드를 구성하는 사인파 주파수로 분해하는 것입니다.

사실, 당신은 그것이 무엇인지 깨닫지 못한 채 그렇게 하도록 설계된 장치를 이미 보았을 것입니다! 그래픽 이퀄라이저 음악의 고조파 콘텐츠의 특성을 제어(때로는 표시)하는 하이파이 스테레오 장비입니다.

여러 개의 노브 또는 슬라이드 레버가 장착된 이퀄라이저는 음악에 존재하는 특정 주파수의 진폭을 선택적으로 감쇠(감소)하여 청취자의 이익을 위해 사운드를 "맞춤형"으로 설정할 수 있습니다. 일반적으로 각 제어 레버 옆에 "막대 그래프"가 표시되어 각 특정 주파수의 진폭을 표시합니다.

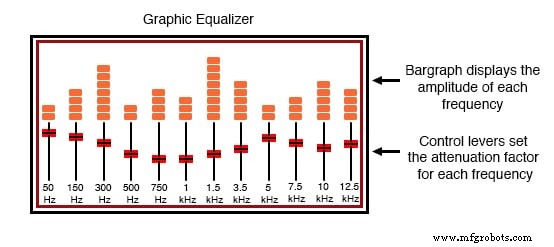
하이파이 오디오 그래픽 이퀄라이저

혼합 주파수 신호에 대한 각 주파수 범위의 진폭을 제어하지 않고 표시하도록 엄격하게 제작된 장치를 일반적으로 스펙트럼 분석기라고 합니다. .

스펙트럼 분석기의 설계는 서로 다른 주파수를 분리하도록 설계된 일련의 "필터" 회로(자세한 내용은 다음 장 참조)처럼 간단하거나 FFT 알고리즘을 실행하는 특수 목적 디지털 컴퓨터처럼 복잡할 수 있습니다. 신호를 고조파 성분으로 수학적으로 분할합니다.

스펙트럼 분석기는 종종 무선 송신기 및 컴퓨터 네트워크 하드웨어에서 생성되는 것과 같은 초고주파 신호를 분석하도록 설계됩니다. 이러한 형태에서는 종종 오실로스코프와 같은 모양을 갖습니다.

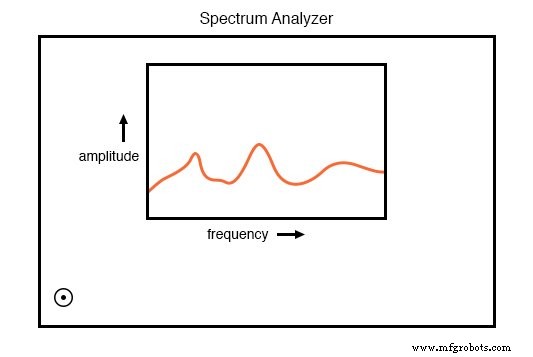
스펙트럼 분석기는 진폭을 주파수의 함수로 보여줍니다.

오실로스코프와 마찬가지로 스펙트럼 분석기는 CRT(또는 CRT를 모방한 컴퓨터 디스플레이)를 사용하여 신호의 플롯을 표시합니다.

오실로스코프와 달리 이 플롯은 주파수에 대한 진폭입니다. 시간에 대한 진폭보다는 . 본질적으로 주파수 분석기는 작업자에게 신호의 Bode 플롯을 제공합니다. 이는 엔지니어가 주파수 영역이라고 부를 수 있는 것입니다. 시간 영역보다는 분석.

"도메인"이라는 용어는 수학적입니다. 그래프의 가로 축을 설명하는 정교한 단어입니다. 따라서 오실로스코프의 시간(수평)에 대한 진폭(수직) 플롯은 "시간 영역" 분석인 반면 스펙트럼 분석기의 주파수(수평)에 대한 진폭(수직) 플롯은 "주파수 영역" 분석입니다.

SPICE를 사용하여 주파수 범위에 걸쳐 신호 진폭(전압 또는 전류 진폭)을 표시할 때 주파수 영역 분석.

마지막 SPICE 시뮬레이션의 푸리에 분석이 "완벽"하지 않다는 점에 유의하십시오. 이상적으로는 모든 짝수 고조파의 진폭이 절대적으로 0이어야 하며 DC 성분도 절대적으로 0이어야 합니다. 다시 말하지만, 이것은 SPICE의 단점이라기보다는 일반적으로 파형의 속성입니다.

무한 기간(무한 주기 수)의 파형은 절대 정밀도로 분석할 수 있지만 컴퓨터에서 분석에 사용할 수 있는 주기가 적을수록 분석의 정확도가 떨어집니다. 푸리에 분석을 통해 파형을 완전한 사인파 파형으로 줄일 수 있는 것은 파형 전체를 설명하는 방정식이 있는 경우에만 가능합니다.

파동이 순환하는 횟수가 적을수록 주파수는 덜 확실합니다. 이 개념을 논리적으로 극단으로 치면 사이클을 완료하지도 않는 파형인 짧은 펄스에는 실제로 주파수가 없습니다. , 그러나 오히려 무한한 주파수 범위로 작동합니다. 이 원칙은 모든에게 공통적입니다. AC 전압 및 전류뿐만 아니라 파동 기반 현상.

주기의 수와 파형의 주파수 구성 요소의 확실성이 직접적으로 관련되어 있다고 말하는 것으로 충분합니다.

여기에서 파동이 여러 주기 동안 계속해서 진동하도록 하여 분석의 정밀도를 향상시킬 수 있으며 결과는 이상과 더욱 일치하는 스펙트럼 분석이 될 것입니다. 다음 분석에서는 간결함을 위해 파형 플롯을 생략했습니다. 정말 긴 구형파일 뿐입니다.

<사전>구형파 v1 1 0 펄스(-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .option limts=1001 .트란 1m 1 .plot tran v(1,0) .4 50 v(1,0) .끝 과도 응답 v(1)의 푸리에 성분 DC 구성 요소 =9.999E-03 고조파 푸리에 정규화 위상 정규화 없음(hz) 구성 요소 구성 요소(deg) 위상(deg) 1 5.000E+01 1.273E+00 1.000000 -1.800 0.000 2 1.000E+02 1.999E-02 0.015704 86.382 88.182 3 1.500E+02 4.238E-01 0.332897 -5.400 -3.600 4 2.000E+02 1.997E-02 0.015688 82.764 84.564 5 2.500E+02 2.536E-01 0.199215 -9.000 -7.200 6 3.000E+02 1.994E-02 0.015663 79.146 80.946 7 3.500E+02 1.804E-01 0.141737 -12.600 -10.800 8 4.000E+02 1.989E-02 0.015627 75.529 77.329 9 4.500E+02 1.396E-01 0.109662 -16.199 -14.399

푸리에 분석 개선

이 분석(위 그림)이 짝수 고조파 주파수 사인파 각각에 대해 더 적은 DC 구성 요소 전압과 더 낮은 진폭을 보여 주는 방법에 주목하십시오. 이 모든 것은 컴퓨터가 더 많은 주기의 파동을 샘플링하도록 했기 때문입니다. 다시 말하지만, 첫 번째 분석의 부정확성은 SPICE의 결함이 아니라 파동 및 신호 분석의 기본 속성입니다.

검토:

<울>

구형파는 진폭이 감소하는 무한한 일련의 홀수 다중 사인파 고조파에 추가된 동일한(기본) 주파수의 사인파와 같습니다.

파형을 샘플링하고 구성하는 사인파 성분을 결정할 수 있는 컴퓨터 알고리즘이 있습니다. 푸리에 변환 알고리즘(특히 고속 푸리에 변환 , 또는 FFT )은 일반적으로 SPICE와 같은 컴퓨터 회로 시뮬레이션 프로그램 및 전력 품질을 결정하기 위한 전자 계량 장비에 사용됩니다.

관련 워크시트:

<울>

구형파 신호 워크시트