전류 분배기 규칙(CDR) – AC 및 DC 회로에 대한 해결된 예

저항성, 유도성 및 용량성 회로용 현재 부문 "CDR"

무엇 는 현재 구분선 규칙(CDR)입니까?

여러 요소가 병렬로 연결되면 전류가 여러 병렬 경로로 나뉩니다. 그리고 전압은 소스 전압과 동일한 모든 요소에 대해 동일합니다.

즉, 전류가 둘 이상의 병렬 경로를 통과할 때(전압 분배 규칙 "VDR" 또는 전압 분할은 직렬 회로의 전압을 계산하는 데 사용됨), 각 경로의 현재 분할. 특정 분기를 통과하는 전류 값은 해당 분기의 임피던스에 따라 달라집니다.

현재 분할 규칙 또는 현재 분할 규칙은 회로를 풀기 위해 널리 사용되는 가장 중요한 공식입니다. 각 가지의 임피던스와 전체 전류를 알면 각 가지에 흐르는 전류를 알 수 있습니다.

전류는 항상 최소 임피던스를 통해 흐릅니다. 따라서 전류는 임피던스와 반비례합니다. 옴의 법칙에 따라 노드에 들어가는 전류는 임피던스에 반비례하여 노드 사이에서 분할됩니다.

전류가 가장 적은 저항 경로를 선택했기 때문에 임피던스 값이 작을수록 더 큰 전류를 가짐을 의미합니다. 그리고 저항값이 클수록 전류가 가장 적습니다.

회로 요소에 따라 전류 분배기 규칙은 저항기, 인덕터 및 커패시터를 설명할 수 있습니다.

저항 회로에 대한 전류 분배기 규칙

저항 전류 분배기 규칙을 이해하기 위해 저항이 병렬로 연결된 회로를 살펴보겠습니다. 회로도는 아래 그림과 같습니다.

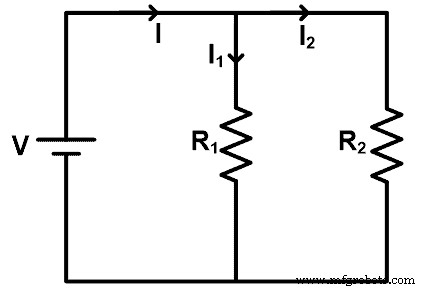
이 예에서 DC 소스는 모든 저항에 공급됩니다. 저항의 전압은 소스 전압과 동일합니다. 그러나 병렬 연결로 인해 전류가 다른 경로로 나뉩니다. 전류는 각 노드에서 분할되며 전류 값은 저항에 따라 달라집니다.

전류 분배기 규칙을 사용하여 각 저항을 통과하는 전류 값을 직접 찾을 수 있습니다.

이 예에서 소스에서 공급하는 주요 전류는 I입니다. 그리고 두 개의 저항 R₁로 나뉩니다. 및 R₂ . 전류는 저항 R₁을 통과합니다. 나는₁입니까? 전류는 저항 R₂를 통과합니다. 나는₂입니까? .

저항이 병렬로 연결되어 있기 때문입니다. 따라서 등가 저항은 R_eq입니다. .

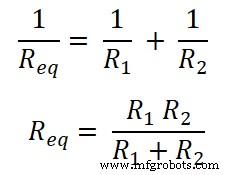
옴의 법칙에 따라

V =I R_eq

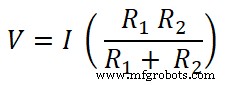
두 저항 모두 DC 소스와 병렬로 연결됩니다. 따라서 저항 양단의 전압은 소스 전압과 동일합니다. 그리고 저항 R₁을 통과하는 전류 나는₁입니까? .

저항 R₁의 경우;

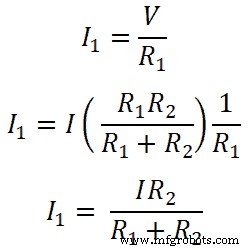
마찬가지로 저항 R₂의 경우;

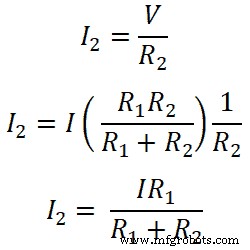
이 방정식은 병렬로 연결된 저항에 대한 전류 분배기 규칙을 보여줍니다. 이 방정식으로부터 저항을 통과하는 전류는 총 전류와 반대 저항을 총 저항에 곱한 비율과 같다고 말할 수 있습니다.

관련 게시물:

• 베냉의 정리. 해결된 예가 있는 단계별 가이드
• Norton의 정리. 해결된 예가 있는 단계별 가이드

유도 회로에 대한 전류 분배기 규칙

인덕터가 병렬로 연결된 경우 전류 분배기 규칙을 적용하여 각 인덕터를 통과하는 전류를 찾을 수 있습니다. 전류 분배기 규칙을 이해하기 위해 아래 그림과 같이 인덕터가 병렬로 연결된 회로를 사용합니다.

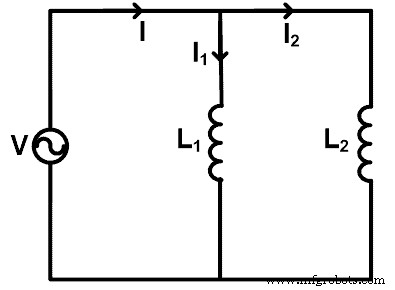
여기에는 두 개의 인덕터(L₁ 및 L₂ ) 소스 전압 V와 병렬로 연결됩니다. 소스를 통과하는 총 전류는 I 암페어입니다. 전류는 인덕터 L₁을 통과합니다. 나는₁입니까? 전류는 인덕터 L₂를 통과합니다. 나는₂입니까? .

이제 현재 I₁에 대한 방정식을 찾아야 합니다. 그리고 나₂ . 이를 위해 등가 인덕턴스 L_eq를 찾을 수 있습니다.;

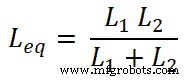
회로를 통과하는 총 전류는 I이고 다음과 같습니다.

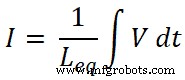
그래서

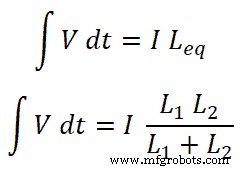
이제 인덕터 L₁에 대해 , 이 인덕터를 통과하는 전류는 I₁입니다.;

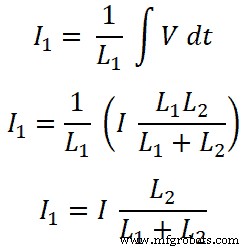
인덕터 L₂용;

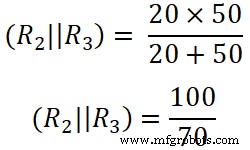
인덕터의 전류 분배기 규칙은 저항의 전류 분배기 규칙과 동일합니다.

용량성 회로에 대한 전류 분배기 규칙

커패시터가 병렬로 연결된 경우 전류 분배기 규칙을 사용하여 각 커패시터에 흐르는 전류를 찾을 수 있습니다. 커패시터에 대한 전류 분배기 규칙을 이해하기 위해 아래 그림과 같이 커패시터를 병렬로 연결하는 예를 들어보겠습니다.

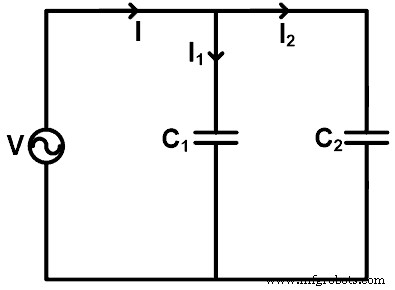
여기에 두 개의 커패시터(C₁ 및 C₂ ) 전압 소스 V와 병렬로 연결됩니다. 전류는 커패시터 C₁를 통과합니다. I_1, 전류는 커패시터 C₂를 통과합니다. 나는₂입니까? . 소스를 통해 공급되는 총 전류는 I입니다.

이제 현재 I₁에 대한 방정식을 찾아야 합니다. 그리고 나₂ . 이를 위해 등가 커패시턴스 C_eq;

C_eq =C ₁ + C ₂

우리는 커패시터를 통과하는 전류에 대한 방정식을 알고 있습니다. 소스에 의해 공급되는 총 전류에 대한 방정식은 다음과 같습니다.

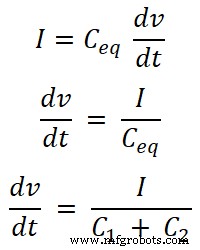
커패시터 C의 경우₁ , 이 커패시터를 통과하는 전류는 I₁;

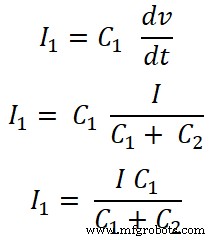
커패시터 C₂의 경우;

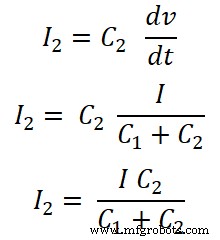
커패시터의 전류 분배기 규칙은 인덕터 및 저항기의 전류 분배기 규칙과 약간 다릅니다.

커패시터 전류 분배기 규칙에서 커패시터를 통과하는 전류는 총 전류에 해당 커패시터를 곱한 총 커패시턴스의 비율입니다.

CDR을 사용한 AC 및 DC 회로의 해결 예

DC 서킷의 현재 다이버 규칙

예:1

주어진 네트워크에 대한 전류 분배기 규칙에 따라 각 저항을 통과하는 전류를 찾습니다.

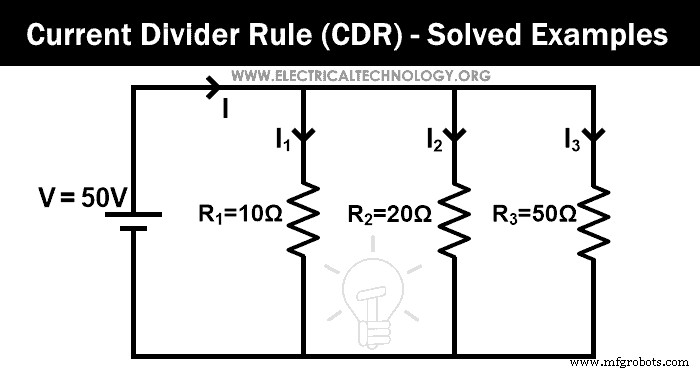
이 예에서는 3개의 저항이 병렬로 연결되어 있습니다. 먼저 등가 저항을 찾습니다.

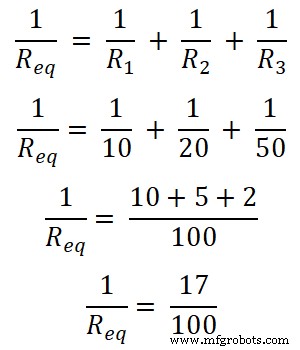
R_eq = 100/17

R_eq = 5.882Ω

소스에서 공급되는 총 전류는 I입니다. 따라서 옴의 법칙에 따라

V =I R_eq

50V =나 (5.882Ω)

나 = 50V / 5.882Ω

나 = 8.5 A

이제 첫 번째 저항(10Ω)에 현재 분배기 규칙을 적용하고 이 저항을 통과하는 전류는 I₁입니다.;

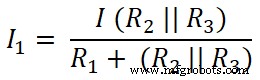
여기 R₂ 및 R₃ 병렬로 연결됩니다. 따라서 R₂ 사이의 등가 저항을 찾아야 합니다. 및 R₃ .

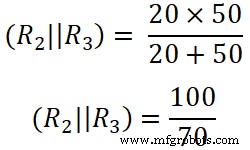
(R ₂ || 알 ₃ ) =14.285Ω

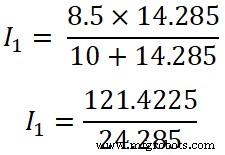
나 ₁ =4.9999 ≈ 5A

마찬가지로 두 번째 저항(20Ω)에 전류 분배기 규칙을 적용하고 이 저항을 통과하는 전류는 I₂입니다.;

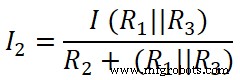
여기

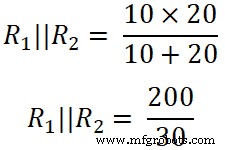
(R ₁ || 알 ₃ ) =8.33Ω

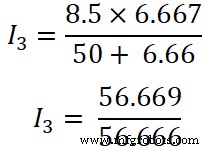
나 ₂ =2.499 ≈ 2.5A

이제 세 번째 저항(50Ω)에 전류 분배기 규칙을 적용하고 이 저항을 통과하는 전류는 I₃ .

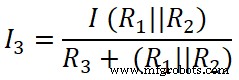
여기

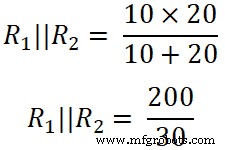
(R ₁ || 알 ₂ ) =6.66Ω

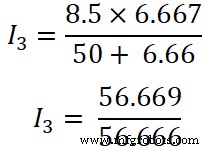
나 ₃ =1.00A

따라서 세 가지 전류의 합계는 다음과 같습니다.

나 ₁ + 나 ₂ + 나 ₃ =5 + 2.5 + 1 =8.5A

이 전류는 소스에서 제공하는 총 전류와 동일합니다.

AC 회로에 대한 현재 다이버 규칙

예제-2

아래 그림과 같이 저항과 커패시터가 병렬로 연결된 AC 회로를 생각해 보십시오. 전류 분배기 규칙을 사용하여 저항과 커패시터를 통과하는 전류를 찾으십시오. 60Hz 주파수를 고려하십시오.

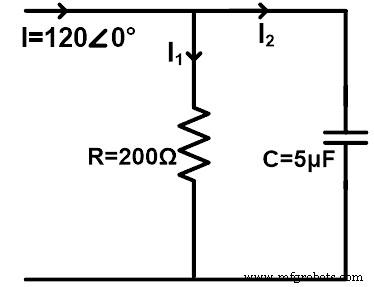
Z_R =200Ω =200∠0°Ω

Z_C =1/(2 πf C) =1/(2 π 60(5×10 ⁶ ) ) )

Z_C =10 ⁶ / (600 π)

Z_C =530.78 ∠-90° Ω

이제 전류 분배기 규칙에 따라 저항을 통과하는 전류 방정식은 다음과 같습니다.

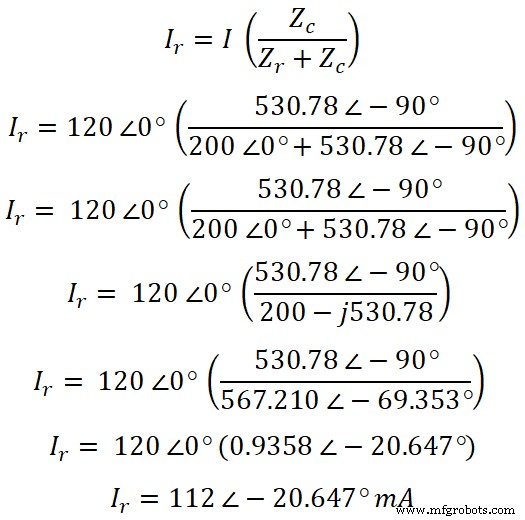
이제 유사하게 커패시터를 통과하는 전류를 찾을 수 있습니다. 전류 분배기 규칙에 따르면 커패시터를 통과하는 전류 방정식은 다음과 같습니다.

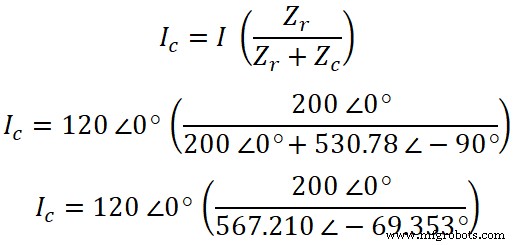
나_C =120 ∠0°(0.3526 ∠ 69.353°)

나_C =42.31 ∠ 69.353°

이 답변을 증명하려면 두 전류를 모두 추가할 수 있습니다. 그리고 이 전류의 값은 소스 전류와 동일합니다.

관련 전기 회로 분석 튜토리얼:

• 보상 정리 – 증명, 설명 및 해결된 예
• 대체 정리 – 해결된 예가 있는 단계별 가이드
• SUPERNODE 회로 분석 – 단계별 해결 예
• SUPERMESH 회로 분석 – 해결된 예와 함께 단계별
• Kirchhoff의 전류 및 전압 법칙(KCL 및 KVL) | 해결 예
• Cramer의 법칙 계산기 – 전기 회로에 대한 2 및 3 방정식 시스템
• Wheatstone Bridge – 회로, 작업, 파생 및 응용
• 전기 및 전자 공학 계산기
• 5000개 이상의 전기 및 전자 공학 공식 및 방정식