보상 정리 – 증명, 설명 및 해결된 예

회로 분석을 위한 보상 정리의 증명, 설명, 실험 및 해결된 예

보상 정리

네트워크 이론에서는 분기 중 하나에서 임피던스 변화의 영향을 알고 연구하는 것이 중요합니다. 네트워크 또는 회로의 해당 전압 및 전류에 영향을 미칩니다. 보상 정리는 네트워크의 변화에 ​​대한 정보를 제공합니다.

보상 정리는 옴의 법칙의 기본 개념에 적용됩니다. 옴의 법칙에 따르면 저항에 전류가 흐르면 저항 양단에 어느 정도의 전압 강하가 발생합니다. 이 전압 강하는 소스 전압에 반대됩니다.

따라서 추가 전압 소스를 소스 전압과 반대 극성으로 연결하고 크기는 전압 강하와 동일합니다. 보상 정리는 이 개념에 적용됩니다.

보상 정리에 따르면

• 관련 게시물:테브냉의 정리. 해결된 예가 있는 단계별 가이드

보상 정리의 설명

보상 정리를 이해하려면 아래 그림을 살펴보세요.

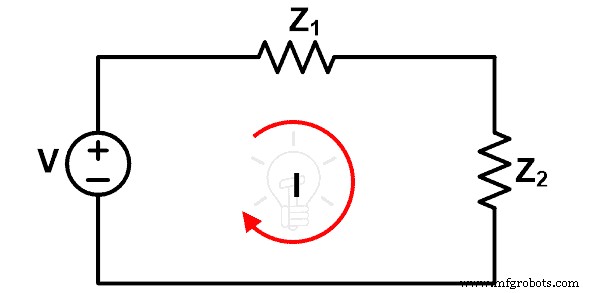
이 그림에서 전압 소스 V는 독립적인 전압 소스와 두 개의 임피던스 Z₁ 및 Z₂ 선형 또는 양방향 요소입니다. 따라서 이 네트워크에 보상 정리를 적용할 수 있습니다. 루프를 통과하는 전류는 I입니다.

이제 임피던스 Z₂ ∆Z만큼 증가합니다. 이 변경으로 인해 루프를 통과하는 전류가 변경되고 I'입니다. 새로운 회로도는 아래 그림과 같습니다.

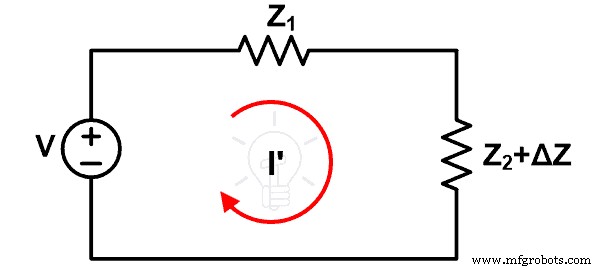
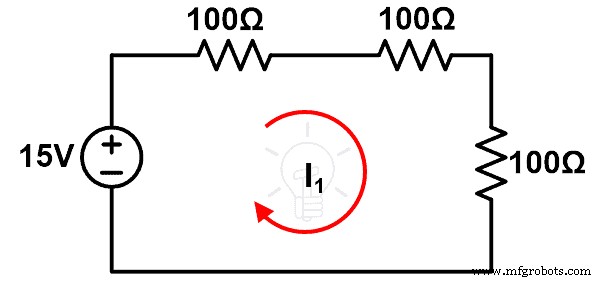
임피던스의 변화로 인해 ∆I에 의해 주어진 전류의 변화

Δ나 =나 – 나

보상 정리의 설명에 따르면 현재 ∆I의 변화를 직접 계산할 수 있습니다. 이를 위해 회로를 수정해야 합니다.

첫 번째 수정은 임피던스가 변경된 분기에 I∆Z 값의 전압 소스를 연결하는 것입니다. 그리고 이 전압원의 극성은 주전원과 반대입니다. 새로 추가된 전압 소스 V_C 보상 소스로 알려져 있습니다.

V_C =나 ΔZ

두 번째 수정은 내부 임피던스에 의해 이전 전압 소스를 제거해야 한다는 것입니다. 이상적인 전압원이라고 생각하면 이 상태에서 단자를 단락시켜 이 전압원을 제거할 수 있습니다. 이러한 수정 후 나머지 회로는 아래 그림과 같습니다.

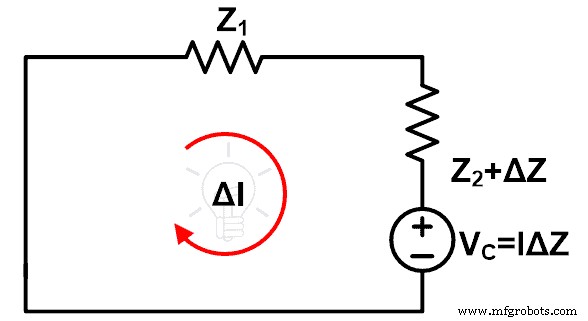
위의 회로를 풀면 임피던스 변화 후 전류 변화를 쉽게 찾을 수 있다.

• 관련 게시물: Norton의 정리. 해결된 예가 있는 단계별 가이드

보상 정리 증명

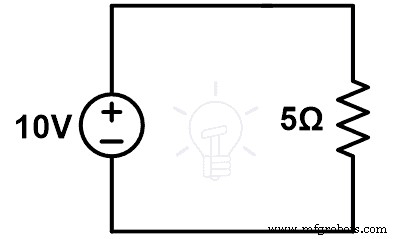
그림-1에 주어진 회로를 고려하십시오. 루프를 통과하는 전류(I)를 계산합니다.

그림-1에 KVL을 적용합니다.

이제 임피던스 Z₂ ∆Z만큼 변경됩니다. 그리고 수정된 회로는 그림-2와 같다. 그림-2의 루프를 통과하는 전류를 계산해야 합니다(I').

그림-2에 KVL을 적용합니다.

임피던스의 변화로 인해 루프 전류의 변화는 ∆I로 표시됩니다. 그리고 ∆I는 기존 전류 I와 새로운 전류 I'의 차이와 같습니다.

Δ나 =나 – 나

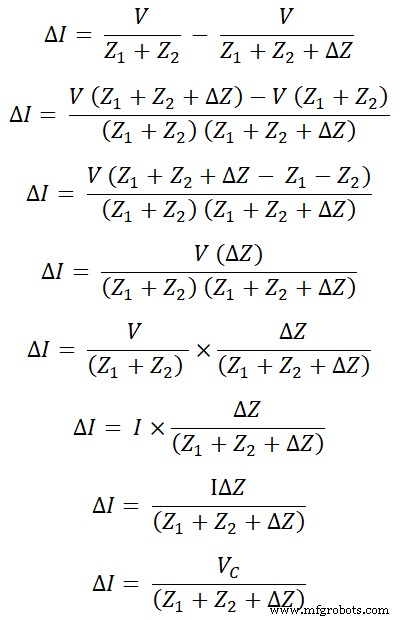
이제 아래 그림을 고려하십시오.

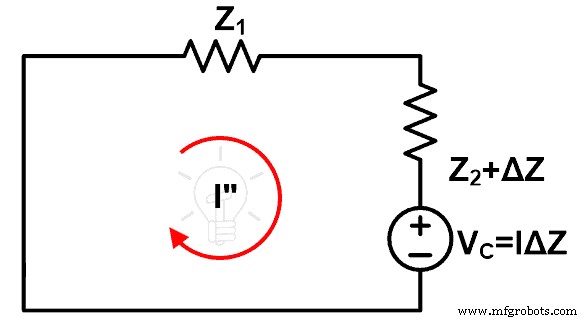
이 그림은 보상 정리를 구현한 후의 회로를 나타냅니다. 여기서 원래의 전압원은 단락에 의해 제거됩니다(이상적인 전압원이라고 가정).

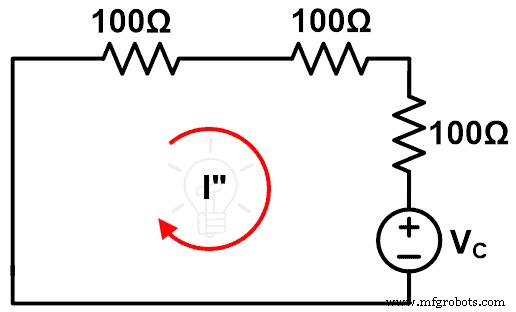
우리는 이 루프를 통해 I인 현재 패스를 찾을 것입니다." 그리고 이 전류를 위에서 계산한 전류와 비교합니다.

루프를 통과하는 전류를 계산하려면 위 그림에 KVL을 적용하세요.

V_C =Z ₁ 나" +(Z ₂ +ΔZ ) 나"

V_C =나" (Z ₁ + Z ₂ + ΔZ )

나" =V_C / (Z ₁ + Z ₂ + ΔZ )

나" =Δ나

따라서 수정 후 전류(∆I)의 변화는 보상 정리에 의해 계산된 전류와 동일함을 증명합니다.

보상 정리의 진술을 증명했습니다.

• 관련 게시물:중첩 정리 – 해결된 예를 통한 회로 분석

보상 정리 실험

목표: 보상 정리를 증명하고 전류의 변화를 찾으십시오.

장치: 전압계, 전류계, 저항기, 연결 전선, 브레드보드,

회로도:

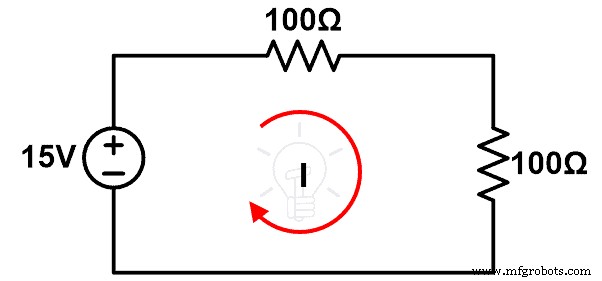
절차:

Step-1 브레드보드에 연결 와이어를 사용하여 그림-5와 같이 구성 요소를 연결합니다.

2단계 현재 I를 측정합니다.

Step-3 그림-6과 같이 컴포넌트를 연결합니다. 여기에 추가 저항을 연결했습니다.

4단계 현재 I1을 측정합니다.

5단계 I 및 I1의 값에서 전류(∆I)의 변화를 계산합니다.

Step-6 그림-7과 같이 컴포넌트를 연결합니다. 이 회로는 보상 회로입니다.

7단계 현재 I 측정".

8단계 현재(∆I)의 변화를 I와 비교합니다.

실험 테이블:

선생님 아니요.	나	나 1	∆나	나"
1

결과:

현재 I''의 값을 ∆I와 비교하여 보상 정리를 증명할 수 있습니다.

• 관련 게시물: Millman의 정리 – AC 및 DC 회로 분석 – 예

보상 정리의 예

예제-1

• 1) 저항이 3Ω일 때 AB 브랜치를 통과하는 전류를 구합니다.
• 2) 3Ω 저항이 9Ω으로 변할 때 보상 정리를 이용하여 가지 AB를 통과하는 전류를 구한다.
• 3) 보상 정리를 증명합니다.

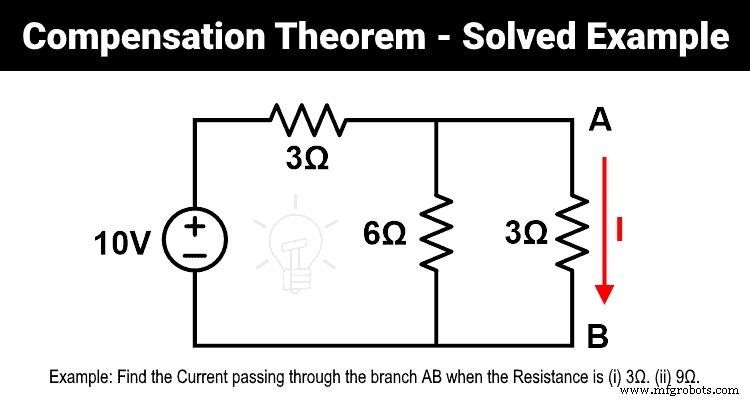
답변-1

그림과 같이 6Ω과 3Ω 저항이 병렬로 연결되어 있습니다. 그리고 이 병렬 조합은 3Ω 저항과 직렬로 연결됩니다. 따라서 등가 저항은 다음과 같습니다.

R _등 =6 | | 3+3

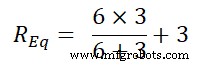
R _등 =2 + 3

R _등 =5Ω

옴의 법칙에 따름;

10 =나 (5)

나 =10 ÷ 5

나 =2A

이제 분기 AB를 통해 현재 패스를 찾아야 합니다. 따라서 현재 구분선 규칙에 따라

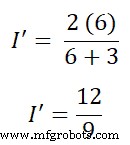
나' =1.333A(또는 3/4A)

• 관련 게시물: 대체 정리 – 해결된 예가 있는 단계별 가이드

답변-2

3Ω 저항을 9Ω 저항으로 교체해야 합니다. 보상 정리에 따르면 9Ω 저항과 직렬로 새로운 전압 소스를 추가해야 합니다. 그리고 이 전압원의 값은;

V_C =나 ΔZ

어디서,

ΔZ =9 – 3 =6 Ω 및 I' =4/3A(또는 1.333A)

V_C =(4/3A) x 6Ω

V_C =8V

수정된 회로도 또는 보상 회로도는 아래 그림과 같습니다.

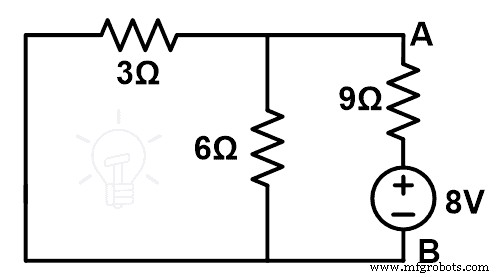
이제 동등한 저항을 찾습니다. 여기서 3Ω과 6Ω 저항은 병렬로 연결됩니다. 그리고 이 병렬 조합은 9Ω 저항과 직렬로 연결됩니다.

R_Eq =3 | | 6 + 9

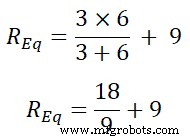
R_Eq =2 + 9

R_Eq =11Ω

옴의 법칙에 따라

V =Δ나는 R

8 =Δ나 (11Ω)

Δ나 =8 ÷ 11

Δ나 =0.7272A

그래서, 보상 정리에 따르면; 전류의 변화는 0.7272A입니다.

• 관련 게시물: Tellegen의 정리 – 해결된 예 및 MATLAB 시뮬레이션

답변-3

보상 정리를 증명하고자 합니다. 따라서 주어진 예에서 9Ω 저항으로 전류를 계산합니다.

수정된 회로도는 아래 그림과 같습니다.

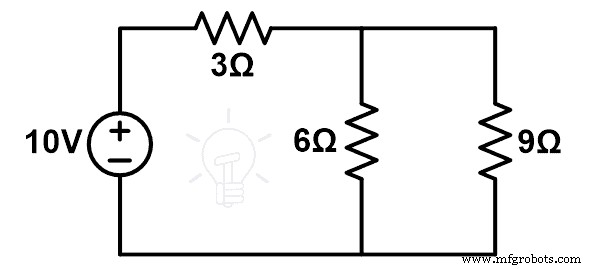
여기서 9Ω과 6Ω 저항을 병렬로 연결하고 이 병렬 조합을 3Ω 저항과 직렬로 연결합니다.

동등한 저항은 다음과 같습니다.

R_Eq =9 | | 6 + 3

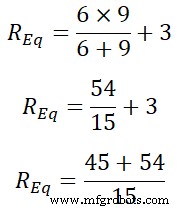
R_Eq =99 ÷ 15

R_Eq =6.66Ω

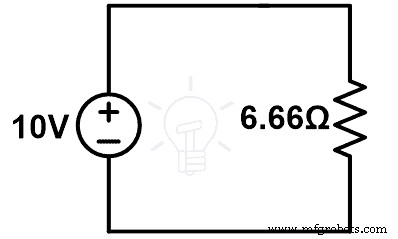
위 그림에서

10 =나 (6.66)

나 =10 ÷ 6.66

나 =1.5151A

현재 구분선 규칙에 따름;

나" =0.6060A

Δ나 =나 – 나"

Δ나 =(4/3A) – 0.6060

Δ나 =1.333A – 0.6060

Δ나 =0.7273A

따라서 보상 정리에서 계산된 전류의 변화는 원래 회로에서 계산된 전류의 변화와 동일함을 증명합니다.

• 관련 게시물:  AC 및 DC 회로의 최대 전력 전달 정리
  

예시 2

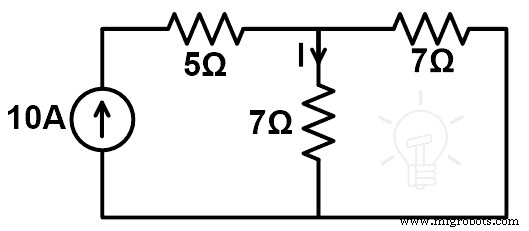
아래 회로에서 보상 정리를 이용하여 3Ω 저항을 7Ω 저항으로 대체했을 때의 전류 변화를 구하라. 그리고 보상 정리를 증명하십시오.

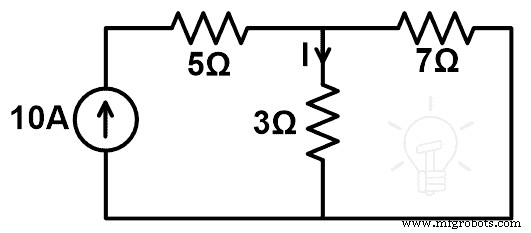
위의 네트워크는 저항과 독립적인 전류 소스로만 구성됩니다. 따라서 이 네트워크에 보상 정리를 적용할 수 있습니다.

이 그림에서 네트워크는 현재 소스에서 제공됩니다. 이제 3Ω 저항 분기를 통과하는 전류를 찾아야 합니다. 이 전류는 KCL 또는 KVL을 사용하여 찾을 수 있습니다. 그러나 여기에서 이 전류는 현재 분할 규칙으로 쉽게 찾을 수 있습니다.

따라서 현재 구분선 규칙에 따라

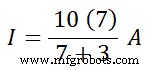
나 =70 ÷ 10A

나 =7A

3Ω 저항이 있는 원래 네트워크에서 해당 분기를 통과하는 전류는 3A입니다. 이제 이 저항을 3Ω에서 7Ω으로 변경해야 합니다. 이 수정으로 인해 해당 분기를 통과하는 전류가 변경됩니다. 그리고 우리는 보상 정리에 의해 이러한 전류의 변화를 찾을 것입니다.

이를 위해서는 보상 네트워크를 만들어야 합니다. 보상 네트워크를 만들려면 전압 소스를 단락시키고 전류 소스를 개방하여 네트워크에서 사용할 수 있는 모든 독립 소스를 제거해야 합니다.

이 네트워크에서는 현재 소스가 하나만 있습니다. 전류 소스가 이상적인 전류 소스라고 가정합니다. 따라서 내부 저항을 추가할 필요가 없습니다.

보상 회로에서 수정해야 할 두 번째 수정 사항은 전압 소스를 추가하는 것입니다. 그리고 이 전압의 값은;

V_C =나 ΔZ

V_C =7 × (7 – 3)

V_C =7 × 4

V_C =28V

보상 네트워크는 아래 그림과 같습니다.

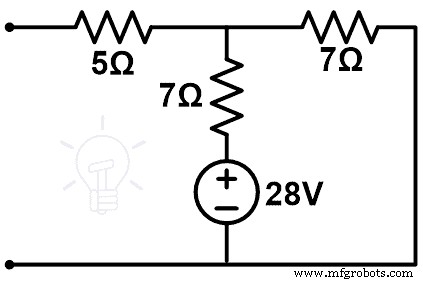
이 그림에는 루프가 하나만 있습니다. 그리고 7Ω의 분기를 통과하는 전류는 우리에게 전류의 변화(∆I)를 줄 것입니다.

Δ나 =V_C ÷ (7+7)

Δ나 =28 ÷ 14

Δ나 =2A

보상 정리를 증명하기 위해 7Ω 저항이 연결된 회로에서 전류를 찾습니다. 수정된 회로도는 아래 그림과 같습니다.

나" =(10 (7)) ÷ (7 + 7)

나" =70 ÷ 14

나" =5A

현재 구분선 규칙을 적용하여

전류의 변화를 찾으려면 원래 네트워크를 통과하는 전류에서 이 전류를 빼야 합니다.

Δ나 =나 – 나"

Δ나 =7 – 5

Δ나 =2A

따라서 우리는 보상 정리를 증명했습니다.

관련 전기 회로 분석 튜토리얼:

• SUPERNODE 회로 분석 – 단계별 해결 예
• SUPERMESH 회로 분석 – 해결된 예와 함께 단계별
• Kirchhoff의 전류 및 전압 법칙(KCL 및 KVL) | 해결 예
• Cramer의 법칙 계산기 – 전기 회로에 대한 2 및 3 방정식 시스템
• 휘트스톤 브리지 – 회로, 작업, 파생 및 응용
• 전기 및 전자 공학 계산기
• 5000개 이상의 전기 및 전자 공학 공식 및 방정식