나노물질
산업 제조
작은 각도 산란(중성자, x-선 또는 빛, SAS)은 결정론적 나노 규모 지방 프랙탈의 구조적 특성을 설명하는 것으로 간주됩니다. 우리는 다분산 프랙탈 시스템의 경우 모든 방향에 대해 동일한 확률로 각 구조 수준에서 프랙탈 차원과 배율 인수를 얻는다는 것을 보여줍니다. 이것은 무작위로 배향되고 상호 작용하지 않는 나노/마이크로 프랙탈 시스템의 작은 각도 산란 분석의 맥락에서 추론된 일반적인 결과와 일치합니다. 산란 강도 및 구조 요인에 대한 분석 표현식을 계산하여 2차원 지방 Cantor와 같은 프랙탈에 결과를 적용합니다. 실험 데이터에서 구조적 특성을 계산하는 방법을 설명하고 반복 횟수에 따른 스케일링 계수의 변화에 대한 상관 관계를 보여줍니다. 모델은 지방 프랙탈의 프레임워크에서 기록된 실험 SAS 데이터를 해석하는 데 사용할 수 있으며 프랙탈 차원의 규칙적인 변경 법칙을 특징으로 하는 재료의 구조적 특성을 나타낼 수 있습니다. 산란 지수의 임의의 감소 값으로 거듭제곱 법칙 붕괴를 설명할 수 있습니다. 및 일정한 강도의 영역에 의해 삽입됩니다.
나노 및 마이크로 스케일에서 생성된 많은 계층 구조는 스케일 확장에 따라 변하지 않는 기하학적 특성을 가지며 자기 유사성을 표시하므로 프랙탈 특성을 나타냅니다[1, 2]. 재료 과학 및 나노 기술의 최근 발전으로 인해 정확한 자기 유사성을 가진 다양한 인공 나노/마이크로 규모 결정론적 프랙탈의 준비가 가능하지만[3-7], 대부분의 자연 과정은 무작위의 통계적으로 자기 유사 프랙탈을 생성합니다. 자연 프랙탈 형성의 구조 연구에서 좋은 근사는 임의의 것과 동일한 프랙탈 차원을 가진 결정론적 프랙탈 모델에 의존하여 수행할 수 있습니다. 이 접근 방식은 무작위 프랙탈 표면을 통한 전달이 결정론적 모델 기하학의 응답에 매우 가깝다는 것을 보여주기 위해 성공적으로 사용되었습니다[8]. 결정론적 프랙탈의 구성 알고리즘에 다분산성을 도입함으로써 무작위 프랙탈에 해당하는 것과 유사한 작은 각도 산란(SAS) 강도를 얻을 수 있습니다[9]. 또한 "결정론적" 접근 방식은 계산적으로 더 효율적이므로 프랙탈 형태, 구조 요소 및 회전 반경과 같은 다양한 속성에 대한 분석적 설명이 가능합니다.
결정론적 프랙탈과 랜덤 프랙탈[10, 11] 모두의 구조적 특성을 결정하는 가장 신뢰할 수 있는 방법 중 하나는 중성자 또는 전자기파를 사용하여 나노 또는 미세 구조 물질에 대한 작은 각도 산란의 맥락에서 파동 회절을 사용하는 것입니다(x - 광선, 빛 등) [12]. 이것이 이 연구 영역의 실험적 결정과 관련된 이론적 설명의 기본 작업 중 하나가 프랙탈의 구조와 해당 회절 스펙트럼 또는 산란 강도 분포 대 산란파 벡터 간의 관계를 밝히는 것입니다. 많은 실험적, 이론적 연구가 이 방향으로 수행되었습니다[13-21].
표준 이론 계산 및 보간법을 사용하여 이러한 종류의 실험 측정에서 결정되는 매개변수는 질량 프랙탈 차원 D입니다. m (부록 1 참조), D m
다양한 화학적 합성 및 생물학적 시스템의 많은 실험적 회절 강도는 이중 대수 규모에서 일정한 강도의 영역에 의해 삽입된 일련의 거듭제곱 법칙 붕괴로 특징지어집니다. 이러한 거동은 일부 고분자 겔[24], 셀로비오스 기질용 배당체 가수분해효소[25], 고분자 전해질 복합 코아세르베이트[26] 또는 나노다공성 탄소[27]에서 확인할 수 있습니다. 고전적인 Beaucage 모델[28]이 이러한 시스템에 대한 기본 구조 정보(즉, 질량 또는 표면 프랙탈 차원 및 각 구조 수준의 전체 크기)를 제공할 수 있지만 프랙탈 차원의 고정 값. 이 문제는 최근 Cherny et al.에 의해 부분적으로 해결되었습니다. 소각 산란(SAS) 모델의 맥락에서. 단일 스케일의 결정론적 질량 프랙탈의 경우 프랙탈 반복 횟수, 기본 구성 단위의 수 및 스케일링 계수와 같은 추가 정보를 얻을 수 있음을 보여주었습니다. 이 접근 방식은 연속적인 거듭제곱 법칙 붕괴가 산란 분포에 있는 경우 지방 프랙탈에 대한 새 모델을 개발하는 데 성공적으로 사용되었습니다. 기본 구성 단위의 전체 크기가 그 사이의 거리와 같은 차수인 구조에 적용할 수 있습니다[30, 31].
이 기사에서 제시하는 이론적 모델은 이전 모델을 결합하여 적용 가능성을 확장합니다. 그것은 산란 지수의 값이 임의로 감소하는 거듭제곱 법칙 붕괴를 설명합니다. 및 일정한 강도의 영역에 의해 삽입됩니다. 우리 모델은 또한 나노/마이크로 프랙탈의 각 구조 수준에 대한 자세한 정보를 제공할 수 있습니다. 이 목적을 위해 우리는 반복 횟수에 따라 달라지는 배율 인수를 가진 2차원 결정론적 질량 프랙탈로 표현되는 지방 프랙탈을 고려하지만 많은 반복 횟수의 한계에서 표면적이 사라지지 않으므로 양의 르베그 측정. 프랙탈 형태와 구조 요인의 해석적 표현을 도출하고, 각 구조적 수준에서 프랙탈 차원과 스케일링 요인을 결정하는 방법을 보여줍니다.
여기에서 Σ로 표시된 유사하게 배향되고 동일한 회절 구멍의 배열을 고려합니다. , N 포함 j로 레이블이 지정된 투명 영역 , 각 조리개에서 얻은 진폭에 대한 합계를 고려해야 합니다. 따라서 단일 구경의 회절 진폭의 잘 알려진 주파수 분포(부록 2의 식 (37))는 [32]와 같이 다시 쓸 수 있습니다.
$$ A(p,s) =\sum\limits_{j=1}^{N} \iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{- 2 i \pi \left(p(x+x_{j}) + s(y+y_{j})\right)}\mathrm{d}x\,\mathrm{d}y. $$ (1)j의 로컬 프레임에 있는 점의 좌표 th 조리개는 (x j ,y j ) 및 T (x,y )는 각 투명 영역에 해당하는 개별 전송 함수를 나타냅니다. 우리의 경우 조리개가 동일한 개별 분포 함수로 설명되기 때문에 통합과 합산을 교환할 수 있습니다. 따라서 Eq. (1) 다음과 같이 다시 쓸 수 있습니다.
$$ A(p,s) =\iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{-2 i \pi (px + sy)}\mathrm{ d}x\,\mathrm{d}y \times \sum\limits_{j=1}^{N}e^{ipx_{j}}e^{isy_{j}}. $$ (2)이전 등식의 적분 계수는 위에서 언급한 바와 같이 동일한 구멍 각각의 분포 함수의 푸리에 변환을 나타냅니다. 이 진폭은 \(A_{\delta }~=~\sum _{j~=~1}^{N}(x~ -~x_{j})(y~~y_{j})\). 따라서 어레이 내부 구멍의 공간 분포도 고려됩니다. 따라서 식. (2) 배열 정리 [32]로 알려진 형식으로 다시 작성할 수 있습니다.
$$ A(p,s)~=~\mathcal{F}\left\{T(x,y)\right\} \mathcal{F}\left\{A_{\delta}\right\}. $$ (3)푸리에 평면에서 회절된 이미지의 강도 분포는 다음과 같습니다.
$$ I(p,s) \equiv \left| A(p,s) \right|^{2} =\left|\mathcal{F}\left\{T(x,y)\right\}\right|^{2} \big|\mathcal{F }\left\{A_{\delta}\right\}\big|^{2}. $$ (4)예상대로 제품의 첫 번째 요소는 단일 구멍의 산란 강도에 해당하고 두 번째 요소는 회절 구멍 Σ 내에서 이러한 구멍이 분포되는 방식을 나타냅니다. . 이러한 양은 폼 팩터 F라고도 합니다. (p,q ) 및 각각 구조 계수 S (p,q ). 그렇기 때문에 논문 전체에서 얻은 결과는 다음과 같은 산란 강도 형식을 사용하여 표현됩니다.
$$ I(p,q) \equiv F(p,s) S(p,s). $$ (5)얇은(일반) Cantor 프랙탈을 구성하는 자세한 절차는 잘 알려져 있습니다[33]. 여기서는 주요 건설 절차만 요약합니다. 위에서 아래로 접근 방식이 채택됩니다. 모서리 l의 초기 정사각형(또는 다른 유클리드 모양)으로 시작 0 (m에 =0), 중심은 데카르트 좌표계의 원점과 일치하고 모서리는 좌표계 축과 평행하며 정사각형의 모든 점은 조건 -l을 충족합니다. 0 /2≤x ≤나 0 /2 및 -l 0 /2≤y ≤나 0 /2. 첫 번째 반복에서(m =1), 정사각형은 모서리 길이가 \(\beta _{\mathrm {s}}^{(1)}l_{0}\)인 네 개의 다른 정사각형으로 나뉩니다. \(\beta _{\mathrm {s}}^{(1)} \equiv (1-\gamma _{1})/2\)로 표시하고 \(0 <\beta _{\mathrm { s}}^{(1)} <1/2\), 첫 번째 반복 배율 인수 및 γ 포함 1 m에 대해 그림 1a, b)에서 볼 수 있는 것처럼 이 지점에서 제거된 길이의 비율 =1. 상위 인덱스로 나타나는 (⋯) 사이의 숫자는 반복 횟수를 수량화합니다. 거듭제곱 함수의 지수로 해석되어서는 안 됩니다. 스케일링 인자의 관점에서, 네 개의 정사각형의 위치는 벡터 \(\boldsymbol {a}_{j}~=~\left \{ \pm \beta _{\mathrm {t}}^{ (1)}l_{0}, \pm \beta _{\mathrm {t}}^{(1)}l_{0}\right \}\) 가능한 모든 기호 조합, 여기서 \(\beta _{ \mathrm {t}}^{(1)}~=~\left (1-\beta _{\mathrm {s}}^{(1)}\right)/2\)는 공식을 더욱 단순화하는 데 사용됩니다. 숫자 계산의 단순성 때문에 사각형이 초기 모양으로 선택되었습니다. 예를 들어 원과 같은 다른 기하학적 모양을 고려할 수 있습니다. 다른 모양을 선택하는 효과는 폼 팩터의 Porod 영역에서만 관찰되며 이는 이 문서의 범위를 벗어납니다.
<그림>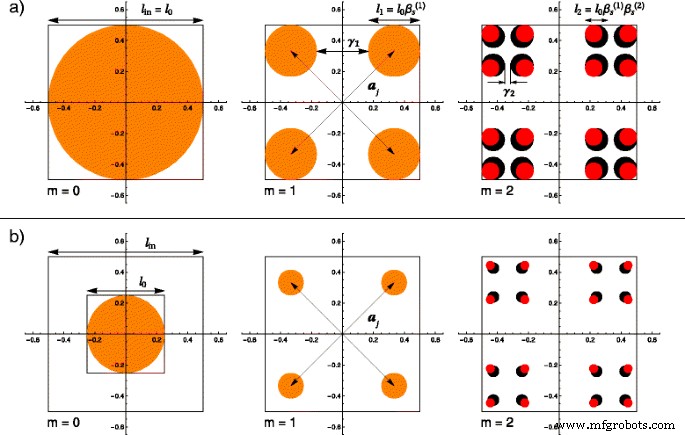
(Color online) m의 기본 모양이 있는 처음 두 반복에 대한 일반 프랙탈과 팻 프랙탈의 비교 =0은 직경이 l인 디스크입니다. 0 프랙탈 크기는 l입니다. 안에 :a 나 0 =나 안에; ㄴ 나 0 =나 안에 /f , f =2. 두 경우 모두 m에서 =1 구조는 동일한 스케일링 계수 \(\beta _{\mathrm {s}}^{(1)}\)로 인해 일치합니다. m로 시작 =2, 지방 프랙탈은 더 큰 배율 인수를 가집니다. \(\left (\beta _{\mathrm {s}}^{(2)}> \beta _{\mathrm {s}}^{(1)}\ right)\) 따라서 디스크의 직경이 더 큽니다(검은색 디스크). ) 일반 프랙탈(빨간색 디스크 ); 아 j 위치 벡터 및 γ 나 i에서 제거된 길이의 분수입니다. 반복
위에서 설명한 처음 두 단계는 m =0 및 m =1. 이것이 지금까지 이 두 구조가 일치하는 이유입니다. 지방 프랙탈을 얻기 위해 반복 m에서 사용된 알고리즘 수정 =1은 m에서 다른 배율 인수를 선택하여 수행해야 합니다. =2, \(\베타 _{\mathrm {s}}^{(2)} \equiv (1 - \감마 _{2})/2\). 높은 반복 횟수[34, 35]의 한계에서 전체 알고리즘을 적용하면 뚱뚱한 프랙탈의 고전적인 버전을 다시 얻습니다. 구성에서 프랙탈의 일반 버전은 각 반복에서 스케일링 계수가 \(\beta _{\mathrm {s}}^{(1)}~=~와 같도록 선택될 때 복구된다는 것이 분명합니다. \베타 _{\mathrm {s}}^{(2)}~=~\cdots =\베타 _{\mathrm {s}}^{(m)}\).
SAS 강도의 거동에서 2개의 거듭제곱 법칙 감쇠 사이의 일정한 안정기를 얻으려면 산란 단위 사이의 거리가 전체 크기보다 훨씬 크다는 점을 고려해야 합니다. 이러한 접근 방식은 표면 프랙탈 모델의 맥락에서 처음 사용되었습니다[36, 37]. f 비율 고려 산란 단위 사이의 전체 거리 l 안에 및 전체 크기 l 0 , 하나는:
$$ f~\equiv~ l_{\text{in}}/l_{0}. $$ (6)두 프랙탈 영역 사이에 일정한 강도의 고원을 표시하는 산란 실험의 경우 f 값 ≫1을 선택해야 합니다. 표면 프랙탈의 경우 f 값 증가 한편으로는 총 SAS 강도와 다른 한편으로는 독립 산란 단위의 근사치 간에 더 나은 일치를 이끌어냅니다[36, 37].
위의 고려 사항을 사용하여 일반 도형과 지방 도형의 차이점을 설명할 수 있습니다. 요인 f의 영향 , 위에서 소개한 도 시각화할 수 있습니다. 이것이 그림 1에서 반경 r의 디스크를 사용하여 비교를 그래픽으로 예시하는 이유입니다. 0 ≡나 0 /2=나 안에 /(2f ) 우리의 기본 모양으로. 그림 1의 각 행에 표시된 처음 두 반복의 결과는 일반 프랙탈(빨간색 디스크로 표시)과 지방 프랙탈(검은색 디스크로 표시)에 대해 얻은 구조를 나타내며, 이 구조도 완전히 중첩될 수 있습니다( 주황색 디스크로 표시됨). 그림 1a로 표시된 행에서 계수 f 고전적 구조와 프랙탈 모양이 얻어지도록 단위와 동일한 것으로 간주됩니다. 그림의 두 번째 행(그림 1b)은 위에 제시된 요인의 영향을 나타냅니다. 이 계산에서 우리는 f의 임의의 값을 선택했습니다. =2. m 반복에서 =0 및 m =1, 두 경우 모두 일반 및 지방 Cantor 집합의 얻은 구조가 동일하고 완전히 중첩됩니다. 이는 일반적인 스케일링 계수로 인해 예상됩니다. 그러나 그림 1의 마지막 이미지 쌍에서 볼 수 있듯이 m =2에서, 지방 프랙탈의 디스크 반지름은 스케일링 계수 \(\beta _{\mathrm {s}}^{(2)}\)가 정의상 일반 것보다 크기 때문에 더 큽니다. 그림 2b의 마지막 이미지에서 디스크 크기는 f 계수의 단일 값이 아니기 때문에 그림 2a의 디스크 크기보다 훨씬 작습니다. .
<그림>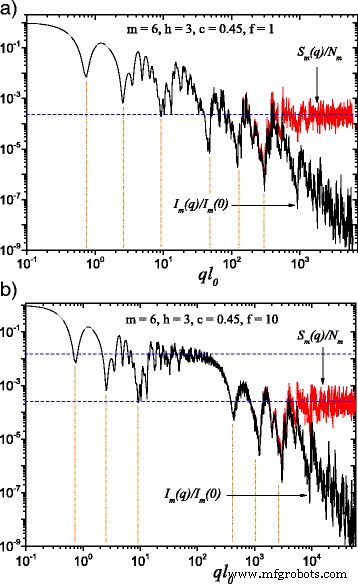
(Color online) Eq.에 의해 주어진 산란 강도 사이의 비교. (22) (검은색 곡선 ) 및 Eq.에 의해 주어진 구조 인자. (24) (빨간색 곡선 ) m에 =6이고 Eq.에 따른 방향에 대한 평균입니다. (25). 여기, h =3(즉, 스케일링 계수는 연속 3회 반복 동안 일정하게 유지됨), 산란 강도 계산의 기본 모양은 모서리 크기 l의 제곱입니다. 0 :a 나 0 =나 안에; ㄴ 나 0 =나 안에 /f (f와 함께 =10). f일 때 ≠1, 두 개의 일반화된 거듭제곱 법칙 감쇠 사이에 일정한 강도의 고원이 나타납니다(그림 2b). 가로선 구조 인자 ≃1/N의 점근선을 나타냅니다. m , 최소 위치는 식에 따라 추정됩니다. (26)
거듭제곱 법칙 자체를 얻으려면 고전적인 지방 프랙탈 모델을 더욱 일반화해야 합니다. 이것은 스케일링 인자 변경이 매 반복마다 수행되는 것이 아니라 매 초, 세 번째, ⋯ 또는 일반적으로 매 h마다 수행된다는 점을 고려하여 수행됩니다. 반복. m에서 제거된 길이의 비율 반복:
$$ \감마_{m}~=~c^{p_{m}}, $$ (7)0<c <1. 기능 p m 는 다음과 같이 정의됩니다.
$$ p_{m} \equiv \left\lfloor 1+\frac{m-1}{h} \right\rfloor, $$ (8)m의 모든 양의 정수 값에 대해 , h =1,⋯,m , 여기서 바닥 함수 ⌊⋯ ⌋가 사용되었습니다. 따라서 m th 반복은 다음과 같이 제공됩니다.
$$ \beta_{\mathrm{s}}^{(m)}~=~\frac{1-\gamma_{m}}{2}. $$ (9)이제 p 함수의 목적이 m h에 대해 배율을 일정하게 유지하는 것입니다. 반복(h <나 ).
각 사각형의 위치 벡터 구성 요소는 다음과 같이 쓸 수 있습니다.
$$ \beta_{\mathrm{t}}^{(m)} =\frac{\beta_{\mathrm{s}}^{(m)}}{2} + \frac{\gamma_{m}} {2}, $$ (10)각 정사각형의 모서리 길이는 다음과 같이 지정됩니다.
$$ l_{m}=\frac{l_{0}}{2^{m}}\prod_{i=1}^{m}(1-\gamma_{i}). $$ (11)계수 f 길이 l의 공식에 사용됩니다. 0 (h +1)번째 및 m th, 정사각형의 크기는 정사각형 사이의 거리에 따라 감소합니다.
$$ l_{0} =\left\{\begin{array}{ll} l_{\text{in}}, &\mathrm{for~~iterations~~} \leq h \\ l_{\text{in }}/f, &\mathrm{for~~iterations~~}> h, \end{array}\right. $$ (12)여기서 h <나 . 각 반복의 제곱 수는 다음과 같습니다.
$$ N_{m}~=~4^{m}. $$ (13)따라서 일정한 스케일링 계수를 사용하는 반복으로 간주되는 모든 스케일에서 [29, 38, 39]에 의해 주어진 다른 프랙탈 차원을 갖습니다.
$$ D_{\mathrm{m}}~=~-\frac{2 \ln 2}{\ln \beta_{\mathrm{s}}^{(m)}}. $$ (14)많은 반복 횟수의 한계에서 구성된 프랙탈 집합의 프랙탈 차원은 [34]가 됩니다.
$$ D \equiv \lim\limits_{m \rightarrow \infty}{\frac{\ln N_{m}}{\ln (l_{0}/l_{m})}} =2, $$ (15 )이것은 2차원 지방 프랙탈의 기대값입니다. 마지막으로 a 나 i에서 제거된 상대 영역입니다. th 반복, \(\prod _{i=1}^{m}(1-a_{i})> 0\) if \(\sum _{i=1}^{\infty } a_{i} <\infty \), 따라서 모델은 지방 프랙탈의 정의와 특성을 만족합니다[35].
Babinet 원리에 따르면 m 반복하면 격자의 구멍은 프랙탈의 나머지 사각형이 되고 제거된 부분은 복사에 불투명해집니다.
지방 칸토어 프랙탈에 대한 산란 강도의 해석적 표현을 유도하기 위해 1D에 해당하는 임의 반복에 대한 격자 투과율의 반복 관계를 작성하는 것으로 시작합니다. 사례. m에 =0,
$$ T_{0}(l_{0}, x) \equiv \text{rect}(l_{0}, x) =\left\{\begin{array}{ll} 1, &|x|여기서 δ (x -아 )는 x에서의 1차원 디랙-델타 분포입니다. =아 . 기호 *는 컨볼루션 연산자를 나타냅니다. 따라서 m에서 반복하면 다음과 같이 작성할 수 있습니다.
$$ \begin{정렬} T_{m}(l_{m}, x) =T_{m-1}(l_{m}, x) \ast \delta\left(\frac{x-u_{m} }{l_{m}} \right) + \\ T_{m-1}(l_{m}, x, y) \ast \delta\left(\frac{x+u_{m}}{l_{m }} \right),~~~~~~~~~~~~ \end{정렬} $$ (18)여기서 \(u_{m}~=~l_{0}\beta _{\mathrm {t}}^{(m)}\prod _{j=1}^{m-1}\beta _{\mathrm {s}}^{(j)}\). 식에서 푸리에 변환을 수행합니다. (18), m에서 산란 진폭이 반복:
$$ A_{m}(p)=2^{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\prod\limits_{i=1}^{ m}\cos(2\pi p u_{i}). $$ (19)2D 이후 뚱뚱한 프랙탈 모델은 2개의 1차원 뚱뚱한 프랙탈의 직접적인 곱이며, 푸리에 변환은 2개의 1차원 푸리에 변환의 곱으로 작성할 수 있습니다. 따라서 2차원 산란 진폭은 다음과 같이 쓸 수 있습니다.
$$ A_{m}(p,s)\equiv A_{m}(p) A_{m}(s), $$ (20)따라서
$$ \begin{정렬} A_{m}(p, s) =N_{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin (\pi s l_{m})}{\pi s l_{m}} \times \\ \prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}), \end{정렬} $$ (21)산란 강도가 다음과 같이 되도록
$$ \begin{정렬} I_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin( \pi s l_{m})}{\pi s l_{m}} \right)^{2} \times \\ N_{m}^{2} \left(\prod\limits_{i=1}^ {m}\cos(2\pi p u_{i})\cos(2\pi s u_{i}) \right)^{2}. \end{정렬} $$ (22)이전 방정식의 첫 번째 요소는 Eq. (5):
$$ F_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin(\pi s l_{ m})}{\pi s l_{m}} \right)^{2}, $$ (23)모서리 l의 단일 정사각형에서 얻은 산란 강도에 해당합니다. m . 두 번째 요인은 구조 요인으로 인한 회절 강도를 나타내며 Eq. (5):
$$ S_{m}(p, s) =N_{m}^{2}\left(\prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}) \right)^{2}, $$ (24)제곱이 분포되는 방식을 설명합니다. 총 산란 복사 강도는 F의 곱입니다. m (p,s ) 및 S m (p,s ).
Eq.에서 공식화된 강도의 거듭제곱 법칙 감쇠입니다. (22)는 모든 방향에 대해 평균을 수행한 후 얻어진다[29]. 모든 방향에 대해 동일한 확률을 고려하면 2차원 프랙탈의 경우 산란 벡터 q의 모든 방향에 대해 통합하여 평균을 계산할 수 있습니다. =(p,s ):
$$ \langle f(p, s) \rangle =\frac{1}{2\pi} \int_{0}^{2\pi}f(q,\phi)\mathrm{d}\phi, $ $ (25)여기서 p =q cosϕ 그리고 s =q 죄ϕ . 따라서 산란 강도 I (q )는 운동량 전달 계수 q의 함수로 얻습니다. ≡|q |.
왜냐하면 구조 인자의 정의에서 \(S_{m}(0)~=~N_{m}^{2}\), 여기서 N m 식에서 정의된 제곱수입니다. (13) 정규화의 표준 절차 S m (0) =1은 [11, 29]에 설명된 대로 채택될 수 있습니다.
단분산 산란 강도 I에 대해 계산된 결과 m (q ) 및 구조 계수 S m (q ), m =6, 고전적인 지방 프랙탈에 대해 그림 2에 표시됩니다(f =그림 2 a)에서 1이고, 이 작업에서 개발된 확장 지방 프랙탈 모델의 경우(f =그림 2 b)의 10. 그림 2b를 얻기 위해 h를 고려했습니다. =3이므로 처음 세 반복의 배율 인수 \(\beta _{\mathrm {s}}^{(1)}\)가 일정하게 유지되고 다른 상수 값 \(\beta _{\ Mathrm {s}}^{(2)}\) 다음 세 번 반복합니다. 예상대로 두 경우 모두(<>f =1 및 f =10), 한편으로는 산란 강도와 다른 한편으로는 구조 인자 간의 차이는 \(q \gtrsim 1/l_{m}\)일 때 관찰할 수 있습니다. 이 영역에서 산란 강도는 거듭제곱 법칙 감쇠 I (q )∝q −3 . 구조 인자는 1/N 경향이 있는 점근적 값을 가집니다. m , 그림 2a의 수평선 또는 그림 2b의 아래쪽 수평선으로 표시 [29, 33].
단순 거듭제곱 법칙 감쇠에 대해 최대값과 최소값의 중첩으로 식별할 수 있는 두 개의 일반화된 거듭제곱 법칙 감쇠의 연속을 그림 2a에서 볼 수 있습니다. 그러나 그림 2b에서 도메인 20≲ql에서 대략 일정한 강도의 영역 0 ≲100은 두 개의 연속적인 일반화된 거듭제곱 법칙 붕괴에 의해 포함되어 명확하게 구별될 수 있습니다. 이것은 정사각형의 크기가 100배 감소하기 때문입니다(f =10) 그들 사이의 거리와 비교. 그림 2b의 위쪽 수평선 주위에서 관찰할 수 있는 이 영역은 점근선 1/N을 갖습니다. 3 , 고전적인 지방 프랙탈의 구조 요인 중 하나와 동일하게 처음 세 번의 반복만 고려하는 경우와 유사한 동작을 나타냅니다.
또한 Fig. 2에서 각 scale에서의 최소값의 수는 일정한 scaling factor의 반복 횟수와 일치함을 알 수 있다. 이러한 최소값은 프랙탈 내부의 다른 정사각형을 통과하는 복사가 간섭하고 위상이 반대일 때 발생하므로 정사각형 중심 사이에서 가장 자주 마주하게 되는 거리(2u m )는 π와 같습니다. /q . 이것이 최소값의 대략적인 위치가 다음 관계에서 얻어지는 이유입니다.
$$ q_{i} \simeq \frac{\pi}{2 u_{i}},~~~~i=1, \cdots, m $$ (26)도 2에서 수직선으로 표시하였다. 처음 6번의 반복에 대해 Eq를 사용하여 계산된 위치 간에 상당히 일치하는 것을 관찰할 수 있습니다. (26), 산란 강도 또는 구조 인자에서 발견되는 것들. 이 근사치는 반복 횟수가 특정 값 이상으로 증가하면 반복 횟수가 많을수록 정확도가 떨어질 수 있습니다. 이러한 경우에 가장 자주 접하는 거리와 점점 더 많은 거리가 비교되기 때문입니다. 그럼에도 불구하고 이 근사치는 실제로 4개 또는 5개 이상의 최소값을 구별할 것으로 거의 기대할 수 없는 경우에 상당히 잘 작동합니다.
각 개별 척도에 대해 주어진 범위에서 1/(2u 나 )≲q ≲1/(2u 나 +1 ), 회절 패턴은 i의 간섭에 의해 생성됩니다. th 프랙탈 반복. 이것은 이 간격 내에서 함수 I m (q )q 디 그리고 S m (q )q 디 로그 주기 [29], 여기서 D 주어진 스케일에 해당하는 프랙탈 차원입니다. 특히, Fig. 2 및 3, 기능 I m (q )q −1.1 그리고 S m (q )q −1.1 처음 세 반복 동안 \(1/\beta _{\mathrm {s}}^{(1)}\) 기간을 갖는 로그 주기적인 반면 I m (q )q −1.51 그리고 S m (q )q −1.51 세 반복의 두 번째 그룹에 대해 \(1/\beta _{\mathrm {s}}^{(2)}\) 로그 주기입니다.
<그림>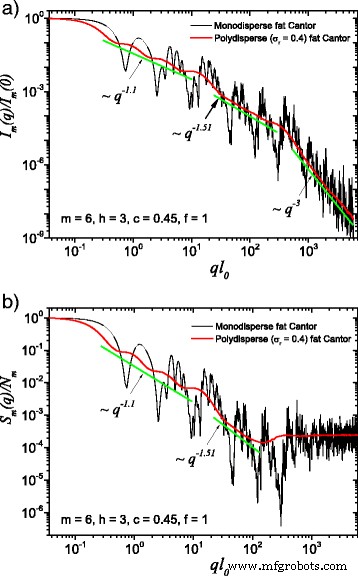
(온라인 컬러) 단분산 시스템과 다분산 시스템의 비교:a 산란 강도(식(22)); ㄴ Eq.(24)), Eq.에 따라 프랙탈의 모든 방향에 대해 평균을 냅니다. (25). 여기서 f =1, m =6, h =3(즉, 스케일링 계수는 세 번의 연속 반복 동안 일정하게 유지됨) 기본 모양은 초기 모서리 길이 l의 제곱입니다. 0 =나 안에 . 두 경우 모두 다분산은 단분산 산란 곡선을 없애고 프랙탈 차원은 각 구조 수준에서 복구할 수 있습니다.
결정론적 질량 프랙탈과 유사한 방식으로 Eq. (26) 지방 프랙탈을 특징짓는 몇 가지 구조적 매개변수를 얻는 데 사용할 수 있습니다. 첫째, 최소값의 총 수는 프랙탈 반복의 총 수와 일치합니다. 그림 2는 프랙탈이 \(\beta _{\mathrm {s}}^{(1)}\) 배율 인수가 있는 세 번의 반복과 \(\beta _{\mathrm {s} 배율이 있는 세 번의 반복으로 구성됨을 보여줍니다. }^{(2)}\). 둘째, 이러한 최소값의 주기성(또는 I m (q )q 디 그리고 S m (q )q 디 ), 스케일링 팩터를 복구할 수 있습니다. 그림 2b에서 스케일링 인자 \(\beta _{\mathrm {s}}^{(1)}\)는 ql에서 최소값의 주기성에서 얻을 수 있습니다. 0 ≃7,25 및 90, 스케일링 계수 \(\beta _{\mathrm {s}}^{(2)}\)는 ql에서 최소값의 주기성에서 얻을 수 있습니다. 0 ≃400,1000 및 2500. 또한, 프랙탈 영역 사이의 중간 고원의 길이는 비율의 표시로 사용할 수 있습니다(f ) 산란 단위 사이의 거리 및 전체 크기. 그림 2b에서 이 범위는 13≲ql에 해당합니다. 0 ≲130.
우리 작업의 이 부분에서 격자 크기가 분포 함수 D를 따르는 것을 고려할 수 있습니다. N (나 0 ), D N (나 0 )dl 0 간격(l)에 있는 프랙탈 격자 크기의 확률을 제공합니다. 0 ,나 0 +dl 0 ). 이 단계는 지방 프랙탈 모델에 다분산성을 도입합니다. 로그 정규 분포를 선택하여 이를 예시합니다.
$$ D_{\mathrm{N}}(l_{0}) =\frac{1}{\sigma l_{0} (2\pi)^{1/2}}e^{-\frac{\left (\log(l_{0}/\mu)+\sigma^{2}/2\right)^{2}}{2\sigma^{2}}}, $$ (27)상대 분산 \(\sigma _{\mathrm {r}} =\left (\left \langle l_{0}^{2} \right \rangle _{D} - \mu ^{2}\right)^ {1/2}/\mu \), 평균값 μ =〈l 0 〉 D , and variance \(\sigma =\left (\log \left (1+\sigma _{\mathrm {r}}^{2}\right)\right)^{1/2}\). Using Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:
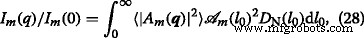
어디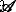 
is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term 
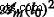[29].
The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f factor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ r , the positions of main minima and maxima are still observable.
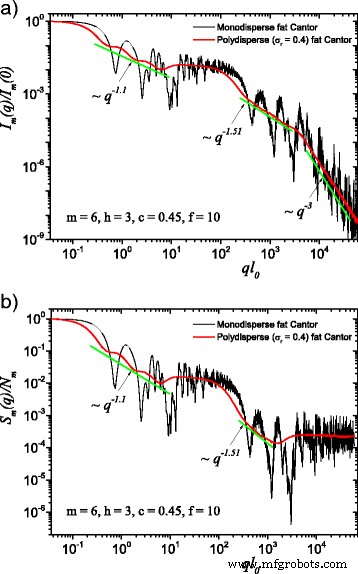
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); ㄴ structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql 0 ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l 0 =l in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level
More generally, for small values of σ r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.
In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.
Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.
We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.
The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.
Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D m ).
In general terms, the mass-radius relation can be rewritten as [2]:
$$ M(r) =A(r) r^{D_{\mathrm{m}}}, $$ (29)where the scaling law correction A (r ) tends to a constant value if r →∞ .
If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l 0 , composed of k elementary units at the first iteration, each of size β s l 0 , where β s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:
$$ M(\beta_{\mathrm{s}}l_{0}) =\beta_{\mathrm{s}}^{D_{\mathrm{m}}}M(l_{0}), $$ (30)one can write M (l 0 )=kM (β s l 0 ). 식을 사용하여 (29), one obtains a direct method to compute the fractal dimension, via:
$$ k \beta_{\mathrm{s}}^{D_{\mathrm{m}}} =1. $$ (31)Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z direction. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:
$$ A(u,v) =\frac{z}{i\lambda} \iint\limits_{\Sigma} A(x,y)\frac{e^{ikr}}{r^{2}} \mathrm{d} x\,\mathrm{d} y. $$ (32)In the previous formula, \(r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}\) is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .
Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:
$$ r \approx z\left(1 + \frac{(u-x)^{2}}{2z^{2}} + \frac{(v-y)^{2}}{2z^{2}}\right). $$ (33)This approximation leads to the Fresnel diffraction integral:
$$ \frac{A(u,v)}{P(u,v)} =\iint\limits_{-\infty}^{~~~+\infty} \left\{A(x,y) e^{i\frac{k}{2z}(x^{2} + y^{2})}\right\} e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y, $$ (34)where the prefactor P (u,v ) is given by
$$ P(u,v) =\frac{e^{ikz}e^{i\frac{k}{2z}(u^{2}+v^{2})}}{i\lambda z}, $$ (35)그리고 k =2π /λ . Considering, in addition, that the condition z ≫k Max(x 2 +y 2 )/2 is satisfied, one has \(\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1\). Rewriting Eq. (34), the Fraunhofer approximation becomes:
$$ A(u,v) =P(u,v)\iint\limits_{-\infty}^{~~~+\infty} A(x,y) e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y. $$ (36)Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space:
$$ A(p,s) =\iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{-2 i \pi (px + sy)}\mathrm{d}x\,\mathrm{d}y. $$ (37)나노물질
목제 태엽 인형은 이미 17세기에 일본에 나타났습니다. 로봇에 대한 일본의 관심은 이후에도 계속됐다. 특히 기모노를 입고 차를 내는 기계는 세계 최초의 로봇 중 하나로 꼽힐 만큼 유명하다. 쟁반에 담긴 찻그릇을 손님에게 옮기고 손님이 그릇을 갈아줄 때까지 기다렸다가 다시 주인에게 돌아왔다. 일본은 다른 일부 국가와 달리 로봇의 위협을 느끼지 않으며 일본의 로봇 기술은 다양한 응용 분야에서 한계를 뛰어넘을 잠재력이 있습니다. 일본에서 탄생한 화낙의 역사는 CNC의 역사 그 자체로 인정받고 있습니다. 1956년에는 일본 민간 부문에서
누군가가 공장용 로봇을 구매하기로 결정하면 프로세스가 빠르게 시작될 수 있지만 일반적으로 작업장에서 승인하고 현실화하는 데 약간의 시간이 걸립니다. 로봇을 구매하는 것은 복잡한 과정이 아니지만 비용이 많이 들 수 있기 때문에 구매하기 바로 전에 모든 것이 제대로 설계되었는지 확인하는 데 시간이 걸립니다. RobotWorx의 전문가가 구매 프로세스를 쉽게 진행할 수 있도록 도와드립니다. 그렇다면 새 로봇을 구입하기로 결정했을 때 가장 먼저 하는 일은 무엇입니까? 통합업체에 접근하기 전에 해당 로봇이 수행할 작업에 대해 어느 정도