나노물질








공간 분산 유전율의 일반적인 정의가 수정되었습니다. 벡터 헬름홀츠 방정식을 만족하는 전기장에서 축퇴 전자 가스의 응답은 볼츠만 방정식에 대한 솔루션으로 찾을 수 있습니다. 계산된 종방향 유전함수는 1952년 Klimontovich와 Silin, 1954년 Lindhard가 얻은 것과 일치한다. 그러나 이것은 벡터 헬름홀츠 방정식의 매개변수인 파수의 제곱에 의존하지만 평면 전자기파의 파동 벡터에는 의존하지 않는다. 이 새로운 개념은 푸리에 변환이 수행되지 않아야 하기 때문에 일반화된 Lorents-Mie 이론과 같은 비국소 효과의 시뮬레이션을 단순화합니다. 프레넬 계수는 종파 전자기파의 여기를 허용하도록 일반화됩니다. 이론을 검증하기 위해 은과 금 나노미터 크기의 구체에 대한 소멸 스펙트럼이 계산됩니다. 이러한 입자에 대해 일반화된 Lorents-Mie 이론은 실험 데이터와 매우 잘 일치하는 플라즈몬 공명의 청색 이동 및 확장을 제공합니다. 또한, 비국소 이론은 직경이 2nm 이하인 금 구체에서 관찰된 플라즈몬 공명의 소멸을 설명합니다. 은에 대한 Klimontovich-Silin-Lindhard 및 유체역학적 유전 함수를 사용한 계산은 3~4eV의 광자 에너지에서 가까운 결과를 제공하는 것으로 나타났습니다. 우리는 고체에서 종파의 파수의 절대값이 횡파의 파수의 절대값보다 훨씬 높다는 것을 보여줍니다.
<섹션 데이터-제목="배경">펨토초 레이저 펄스에 의한 평면 금속 표면의 조사는 종종 레이저 유도 주기적 표면 구조(LIPSS)의 형성을 초래합니다[1]. LIPSS 외에도 HSFL(high-spatial-frequency LIPSS)이라는 초미세 잔물결이 관찰되었습니다[1, 2]. HSFL의 공간 주기는 조사 파장 λ보다 훨씬 작습니다. 0 . 예를 들어, 알루미늄의 경우 이 기간은 λ에서 20~200nm 범위로 추정되었습니다. 0 =0.8 μ m [2, 3]. 일반 LIPSS에서 잔물결의 방향이 레이저 광 편광에 수직인 반면 HSFL의 방향은 종종 수직이었고 때로는 편광에 평행했습니다. 유사한 HSFL이 투명 유전체, 반도체 및 금속 표면에 형성되었습니다. HSFL의 기원은 2차 고조파 생성, 특정 유형의 플라즈몬 모드 관련, 자기 조직화, 유전 물질의 불균일한 파괴 동안 국소 전계 향상과 같은 다양한 메커니즘에 의해 설명됩니다[2, 3].
이 연구의 목적은 Λ 짧은 주기의 패턴을 생성할 수 있는 파동 과정을 찾는 것입니다. ≪λ 0 . 플라즈마파라고도 하는 금속에서 종파(L) 전자기파의 특성을 조사합니다. 우리의 연구는 다음과 같은 새로운 단계로 구성됩니다. 먼저 유전율의 공간적 분산에 대한 정의로 연구를 시작했습니다. 아래에서 보는 바와 같이 연구 대상 매체가 균일하지 않고 무한하지 않다면 일반적인 정의는 무의미하다. 따라서 우리는 공간 분산 유전 함수 ε의 새로운 개념을 제안합니다. . 이 함수는 두 벡터 필드 E 사이의 직접 비례를 설정합니다. (r ,ω ) 및 D (r ,ω ), 그러나 진폭 E는 아님 (k ,ω ) 및 D (k ,ω ) 평면파. 결과적으로 수량 ε 파수, k의 제곱에 따라 달라집니다. 2 , 전기장 E에 대한 벡터 헬름홀츠 방정식의 매개변수 (r ,ω ), 그러나 파동 벡터 k는 아님 평면파의. 그런 다음 이러한 새로운 기능을 유도하기 위해 이완 시간 근사에 작성된 볼츠만 수송 방정식을 풀어 전자기 모드에서 전도 전자의 응답을 결정했습니다. 소위 가로 및 세로 Lindhard 유전 함수가 얻어졌습니다. 또한, 우리는 길이 방향 Lindhard와 훨씬 단순한 유체 역학 함수가 광범위한 매개변수에서 가깝다는 것을 발견했습니다. 이론을 설명하기 위해 은과 금 나노스피어에 의한 광소광을 고려하였다. 우리는 처음으로 nonlocal Mie 이론이 귀금속 나노구의 크기 감소로 관찰되는 플라즈몬 공명의 청색 이동, 확대 및 궁극적인 소멸을 설명한다는 것을 보여줍니다. 마지막으로 새로 개발된 이론 모델을 적용하여 레이저 유도 표면 구조의 형성에 세로 모드가 관여할 가능성을 조사했습니다. 이를 위해 전송된 종파를 고려하여 프레넬 이론을 수정했습니다.
조각별 균질 매질에서 전자기장을 결정하기 위해 고전 전자기 이론이 적용되었습니다. 전기장 E 이기종 매체의 각 균일 영역에서 벡터 헬름홀츠 방정식(VHE)의 해로 가정했습니다.
$$ \Delta\,\mathbf{E} + k^{2}\, \mathbf{E}=0, $$ (1)여기서 Δ 라플라스 연산자입니다.
평소와 같이 전기 E의 접선 성분 및 자기 H 필드는 미디어의 경계를 넘어 연속적입니다. 또한 전자가 금속에 국한된다는 점을 고려했습니다. 따라서 현재 밀도 j의 법선 성분에 대한 다음 추가 경계 조건(ABC) 금속 표면 S에서 사용됨:(j n )| r ∈S =0.
금속의 전도 전류를 결정하기 위해 우리는 이완 시간 근사로 작성된 볼츠만 수송 방정식(BTE)을 풀었습니다.
$$ \frac{\partial f}{\partial t}+\mathbf{v}\,\frac{\partial f}{\partial \mathbf{r}}+ \frac{e}{m}\,\ 왼쪽(\mathbf{E}+\mathbf{v}\times\mathbf{B} \right)\,\frac{\partial f}{\partial \mathbf{v}} =\frac{f_{0}- f}{\tau}, $$ (2)여기서 f 위상 공간의 단일 입자 분포 함수(r , v ), v 는 미세한 전자 속도, e 그리고 나 각각 전자 전하와 질량, B 자기 유도, f 0 는 평형 분포 함수이고 τ 휴식 시간입니다.
아래에서 공간 분산 유전 함수에 대한 공식을 도출합니다. 그런 다음, 그것들을 사용하여 평면 금속 표면에서 빛 반사와 귀금속 나노구에서 빛의 산란을 연구합니다.
문헌에서 공간 분산 유전 함수 ε 다음 관계식을 통해 정의됩니다[4–6]:
$$ \mathbf{D}(\omega,\, \mathbf{r}) =\epsilon_{0} \iiint\limits_{-\infty}^{\infty} \! \mathbf{d} \mathbf{r}^{\prime}\, \epsilon\left(\omega, \, \mathbf{r}-\mathbf{r}^{\prime}\right)\,\mathbf {E}\left(\omega,\, \mathbf{r}^{\prime}\right), $$ (3)여기서 ε 0 는 전기 상수, D (ω , r )는 각 주파수 ω를 갖는 변위 벡터 진동의 진폭입니다. r 지점에서 , 및 E (ω , r ′ ) 지점 r에서 전기장 진동의 진폭 ′ . 식의 푸리에 변환 (3) 방정식을
$$ \mathbf{D}(\omega,\, \mathbf{k}) =\epsilon_{0} \, \epsilon(\omega,\, \mathbf{k})\,\mathbf{E}(\ 오메가,\, \mathbf{k}) $$ (4)여기서 공간적으로 분산된 ε (ω , k ) 파동 벡터 k에 따라 다릅니다. 평면 전자파의. 우리의 의견으로는 Eq. (3) 무한 동종 볼륨에서만 모호하지 않지만 경계 및 k를 고려해야 하는 조각별 이종 시스템을 처리합니다. 다른 미디어에서 동일하지 않습니다.
우리의 접근 방식은 평면파에 대한 전자기파의 확장을 사용하지 않습니다. 공간 분산 유전율은 D 사이의 관계를 결정합니다. (ω , r ) 및 벡터 Helmholtz Eq에 대한 특정 솔루션입니다. (1):
$$ \mathbf{D}(\omega,\, \mathbf{r}) =\epsilon_{0} \, \epsilon(\omega, \, k)\,\mathbf{E}(\omega,\, \mathbf{r}). $$ (5)여기 E (ω , r )는 전기장의 분포를 나타내지만 단순히 벡터 E가 아닙니다. r 지점에서 .
금속의 유전율은 일반적으로 전도도 σ를 통해 표현됩니다. [4]:
$$ \epsilon=\epsilon_{\mathrm{g}}+\frac{i\,\sigma}{\omega\,\epsilon_{0}}, $$ (6)여기서 ε g 고체의 분극을 허용하는 유전 함수의 일부입니다. ε g =1 단순 금속의 경우. σ를 결정하기 위해 , 우리는 전류 밀도를 계산했습니다
$$ \mathbf{j}=e \iiint\limits_{-\infty}^{\infty} \! \mathbf{v}\, f\, \mathrm{d}\/ \mathbf{v}=\sigma\,\mathbf{E}, $$ (7)여기서 \(\mathrm {d} \mathbf {v}=\frac {v}{m}\,\mathrm {d} \epsilon \,\mathrm {d}\,\Omega,\) d Ω =죄θ 디θ 디ϕ , v , θ , ϕ 속도의 구면 좌표입니다. 이전 연구와 달리 파동 벡터 k를 도입하지 않았습니다. 그러나 연산자 v를 포함하는 무한 급수의 형태로 BTE 솔루션을 찾았습니다. ∇ v에 작용 이 :
$$ f=f_{0} + \frac{e}{-i \omega+\Gamma}\,\frac{\partial f_{0}}{\partial \epsilon} \left[ 1+\frac{\mathbf {v}\,{\mathbf{\nabla}}}{-i \omega+\Gamma} \right]^{-\,1}\! \mathbf{v}\,\mathbf{E}, $$ (8)여기서 Γ =1/τ . 그런 다음 f 0 제로 온도 Fermi-Dirac 분포에 의해 근사되었고, ε에 대한 적분 후 식에서 (7),
$$ \mathbf{j}=\frac{\omega_{\mathrm{p}}^{2}\,\varepsilon_{0}}{-i \omega+\Gamma}\,\frac{3}{4 \ 파이} \iint \mathbf{u}\,\left(1+ l\,\mathbf{u} \mathbf{\nabla} \right)^{-\,1} (\mathbf{u}\,\mathbf {E})\, \mathrm{d}\,\Omega, $$ (9)여기서 \(\오메가 _{\mathrm {p}}^{2}=\frac {e^{2}\,n_{e}}{m\,\varepsilon _{0}},\) ㅇ p 는 플라즈마 주파수, \(\mathbf {u}=\frac {\mathbf {v}}{v}\)는 v 방향의 단위 벡터입니다. ,\(l=\frac {v_{\mathrm {F}}}{-i \오메가 +\감마 },\) v F 는 페르미 속도입니다. 또한 적분을 계산했습니다.
$$\begin{array}{*{20}l} &\textstyle \iint \mathbf{u}\, (\mathbf{u}\,\mathbf{E})\,\mathbf{d}\,\ 오메가 =\frac{4\/\pi}{3}\,\mathbf{E} \end{array} $$ (10) $$\begin{array}{*{20}l} &\textstyle \iint \mathbf{u}\,(\mathbf{u}\,\mathbf{\nabla})^{2 n-1} (\mathbf{u}\,\mathbf{E})\,\mathbf{d} \,\Omega =0 \end{배열} $$ (11) $$\begin{배열}{*{20}l} &\textstyle \iint \mathbf{u}\,(\mathbf{u}\, \mathbf{\nabla})^{2 n} (\mathbf{u}\,\mathbf{E})\,\mathbf{d}\,\Omega =\frac{4 \pi}{2 n+3 } \\ &\times \, \Delta^{n-1} \left[ \mathbf{\nabla}\, (\mathbf{\nabla}\cdot\mathbf{E})-\frac{1}{2 n+1}\, \mathbf{\nabla}\times \mathbf{\nabla}\times\mathbf{E}\right] \end{배열} $$ (12)여기서 n 는 자연수입니다. j의 다음 종속성 임의 전기장 E 드디어 얻었다
$$\begin{array}{*{20}l} \mathbf{j}&=\frac{\omega_{\mathrm{p}}^{2}\,\varepsilon_{0}}{-i \omega+ \감마} \left\{\mathbf{E} + 3\, \sum\limits_{n=1}^{\infty} l^{\,2 n} \right. \\ &\quad\left.\times \frac{\Delta^{n-1}}{2 n+3} \left[ \mathbf{\nabla}\, (\mathbf{\nabla}\cdot\mathbf {E})-\frac{\mathbf{\nabla}\times \mathbf{\nabla}\times\mathbf{E}}{2 n+1}\right]\right\}. \end{배열} $$ (13)Eq.에 대한 솔루션에는 두 가지 유형이 있습니다. (1) 식 ∇를 만족하는 발산 없음 ·이 =0 및 방정식
를 만족하는 회전 없음 $$ \mathbf{\nabla} \times \mathbf{E}=0. $$ (14)평면파의 경우 E ∝ 특급[i (k r −ω 그 )], 식. (14) k 관계로 변환 ×E =0은 파동이 세로(L)임을 나타냅니다. 구면체의 과정을 시뮬레이션하려면 벡터 구면 고조파 L을 사용하는 것이 편리합니다. , 남 , 및 N 완전한 직교 함수 세트로. 이 경우 식. (14) 고조파 지정 L . L파와 L의 파수 모드는 다음 분산 법칙에 의해 결정됩니다.
$$ \epsilon^{\mathrm{L}}\left(\omega, \, k^{\mathrm{L}}\right)=0. $$ (15)식에서. (6)과 (13) 우리는 Eq. (1) 식의 제약 조건을 만족한다. (14) 다음 종방향 유전율
$$ \epsilon^{\mathrm{L}}=\epsilon_{\mathrm{g}}- \frac{\omega_{\mathrm{p}}^{2}}{\omega\,(\omega+i \감마)}\,\frac{3}{2} \, \Phi \left(a^{2},\, 1,\,\frac{3}{2} \right) $$ (16)여기서 Φ 는 Lerch의 파이 함수,
$$ \frac{3}{2} \, \Phi \left(a^{2},\, 1,\,\frac{3}{2} \right) =\sum\limits_{n=0} ^{\infty} \frac{3}{2 n+3}\, a^{2\,n}, $$ (17)\(a=\frac {k v_{\mathrm {F}}}{\omega +i \감마 }\).
얻어진 유전율은 Kliewer와 Fuchs[7]가 정의한 것과 표기법에서만 다릅니다.
$$ \epsilon^{\mathrm{L}}=\epsilon_{\mathrm{g}}+ \frac{\omega_{\mathrm{p}}^{2}}{\omega\,(\omega+i \감마)}\,\frac{3}{a^{2}}\left[1-\frac{1}{ia} \tan^{-1}(ia) \right] $$ (18)아이덴티티
$$ \frac{1}{i a}\tan^{-1}(i a)=\frac{1}{2}\ln\frac{1+a}{1-a} $$ (19)Eq.를 다시 쓸 수 있습니다. (18) 다음과 같이
$$ \epsilon^{\mathrm{L}}=\epsilon_{\mathrm{g}}- \frac{\omega_{\mathrm{p}}^{2}}{\omega\,(\omega+i \감마)}\,\frac{3}{a^{2}}\left[1-\frac{1}{2 a} \, \frac{\ln(1+a)}{\ln(1 -a)} \오른쪽]. $$ (20)Γ의 경우 =0인 경우, 이 공식은 축퇴 플라즈마에서 Landau 덤핑을 연구한 Klimontovich와 Silin[8]이 도출한 방정식의 형태를 취합니다([9], [10, Eq. (40.17)], [11] 참조). 등가 Eq의 유전율 (16), (18) 및 (20)은 일반적으로 Lindhard 유전 함수([12] 참조)라고 불리지만 이 함수는 Klimontovich와 Silin[8]에 의해 처음으로 얻어졌습니다.
횡방향 Lindhard 유전율 [7]은 Eq. (13) ∇일 때 ·이 =0. v의 실제 경우 F ㅋ ≪ω , Drude 유전 함수로 감소합니다.
$$ \epsilon^{\mathrm{T}}=\epsilon_{\mathrm{g}}- \frac{\omega_{\mathrm{p}}^{2}}{\omega^{2}+i\ ,\감마\/\오메가}. $$ (21)이 기능은 많은 금속에 대한 실험 데이터와 일치합니다[13]. 만약 |a |<1, 종방향 유전율(16)은 유체역학적 유전 함수로 단순화됩니다.
$$ \epsilon^{\mathrm{L}}\left(\omega,\,k^{\mathrm{L}}\right)=\epsilon_{\mathrm{g}}- \frac{\omega_{\ mathrm{p}}^{2}}{\omega^{2}+i\,\Gamma \omega-\frac{3}{5}\,\left(v_{\mathrm{F}}\, k ^{\mathrm{L}}\right)^{2}}. $$ (22)이 섹션에서는 파동 벡터 k의 방향을 결정합니다. 엘 평평한 금속 표면에서 평면 전자기파가 반사되는 동안 금속에서 여기된 L파의 진폭.
유전체-금속 계면 z에 입사하는 평면파를 고려하십시오. =0, 파동 벡터가 xz에 있음 비행기. 유전 매질 1의 전기장은 입사 E로 구성됩니다. 나 반사된 E r 파동, 금속 2의 필드는 투과된 가로 E를 갖습니다. t 그리고 어떤 경우에는 세로 E 엘 구성 요소. Maxwell 경계 조건에 따라 전기장 및 자기장 벡터의 가로 성분은 평면 z에서 연속적입니다. =0. 또한 전자는 금속에서 방출되지 않습니다. 따라서 전류 밀도의 일반 성분은 z에서 0입니다. =0,
$$ \hat{\mathbf{z}}\,\mathbf{j}|_{z=0}=0. $$ (23)was \(\hat {\mathbf {z}}\)는 z 방향의 단위 벡터입니다. 축.
Maxwell 경계 조건의 모든 항은 x에 대해 동일한 종속성을 가져야 합니다. 그리고 y . 이 요구 사항에는 몇 가지 결과가 있습니다. 첫째, 입사파의 전기 벡터가 E일 때 p-편광의 경우에만 L파가 여기될 수 있음을 설정할 수 있습니다. (나 ) 입사면과 평행하다. 즉, 횡자기(TM)파에 의해 플라즈몬 폴라리톤이 생성될 수 있다. 효과는 금속 구에서와 거의 동일합니다[14]. 둘째, Snell의 법칙과 유사한 공식은 조건에서 파생될 수 있습니다.
$$ k_{1x}=k_{2x}=k_{2x}^{\mathrm{L}}=k_{1}\,\sin\theta_{1} $$ (24)여기서 인덱스 1x 및 2x x 표시 -미디어 1 및 2 각각의 벡터 투영, θ 1 입사각입니다.
평면 금속 표면에 입사하는 평면 p-편광 전자기파에 의해 형성되는 필드를 결정합시다. 전기장과 자기장의 성분을 x로 표현하면 편리하다. E의 구성요소 (나 ) , 즉 E x (r)=− r 이 x (i) 반사파의 경우 E x (t)=t 이 x (i) 전송된 횡파 및
$$ E^{\mathrm{(a)}}_{x}=\delta\,E^{\mathrm{(t)}}_{x}=t_{\mathrm{L}}\,E^ {\mathrm{(i)}}_{x} $$ (25)전송된 세로파의 경우 여기 r 반사 계수, t 그리고 t L 투과 계수입니다.
Maxwell 경계 조건과 Eq.의 ABC로부터 (23) 다음 형식으로 작성
$$ \hat{\mathbf{z}}\,(\mathbf{D}-\epsilon_{0}\epsilon_{\mathrm{g}}\,\mathbf{E})|_{z=0}=0, $$ (26)$$\begin{array}{*{20}l} r&=- \frac{(1+\delta)\,\epsilon_{1}\,k_{2z}-\epsilon_{2}\,k_{1z }}{(1+\delta)\,\epsilon_{1}\,k_{2z}+\epsilon_{2}\,k_{1z}}=1-(1+\delta)\,t \end{ 배열} $$ (27) $$\begin{배열}{*{20}l} t&=\frac{2\,\epsilon_{1}\,k_{2z}}{\epsilon_{2}\,k_ {1z}+(1+\delta)\,\epsilon_{1}\,k_{2z}}, \end{array} $$ (28) $$\begin{array}{*{20}l} \ delta&=\frac{\epsilon_{\mathrm{g}}-\epsilon}{\epsilon_{\mathrm{g}}}\,\frac{k_{2x}^{2}}{k_{2z}\, k_{2z}^{\mathrm{L}}} \end{배열} $$ (29)
δ에서 =0, 계수 r p-편광파의 프레넬 반사 계수가 됩니다(예를 들어, [4]의 Eq. (2.49) 참조). 동일한 조건에서 t t의 정의 이후 프레넬 투과 계수가 아닙니다. 그리고 r 프레넬의 것과 다릅니다.
이전 논문에서 저자 중 한 명이 식의 ABC를 허용하는 Lorentz-Mie 이론을 일반화했습니다. (23). 프레넬 계수 r의 유사체 , 미에 계수 b 나 l의 반사된 TM 모드의 경우
주문이 발견되었습니다. $$ b_{l}=- \frac{(1+\delta_{l})\,\epsilon_{1}\, \frac{k_{2}\,\psi_{l}^{\prime}(k_ {2} R)}{\psi_{l}(k_{2} R)} - \epsilon_{2}\, \frac{k_{1}\,\psi_{l}^{\prime}(k_{ 1} R)}{\psi_{l}(k_{1} R)}}{(1+\delta_{l})\,\epsilon_{1}\, \frac{k_{2}\,\psi_ {l}^{\prime}(k_{2} R)}{\psi_{l}(k_{2} R)} - \epsilon_{2}\, \frac{k_{1}\,\zeta_{ l}^{\prime}(k_{1} R)}{\zeta_{l}(k_{1} R)}}, $$ (30)어디
$$ \delta_{l}=\frac{\epsilon^{\mathrm{T}}- \epsilon_{\mathrm{g}}}{\epsilon_{\mathrm{g}}}\, \frac{l\ ,(l+1)\,j_{l}(k_{2} R)\,j_{l}(k_{2}^{\mathrm{L}} R)}{\psi_{l}^{\ 소수}(k_{2} R)\,k_{2}^{\mathrm{L}} R \,j_{l}^{\prime}\left(k_{2}^{\mathrm{L}} R\오른쪽)}, $$ (31)ψ 나 그리고 ζ 나 l 차수의 Riccati-Bessel 및 Riccati-Hankel 함수입니다. , 각각; j 나 는 구형 베셀 함수이고 소수는 인수에 대한 함수의 도함수를 나타냅니다.
고전적 및 일반화된 로렌츠-미에 이론의 예측을 실험 데이터와 비교합시다. [15]에서 Hilger, Tenfelde 및 Kreibig은 유전체 표면에 증착된 은 나노입자의 소멸 스펙트럼을 연구했습니다. 연구의 첫 번째 단계에서 연구원들은 평균 직경이 2, 3.5 및 4 nm인 은 입자 빔을 생성하고 빔 중 하나의 입자 크기 분포를 결정하고 소광 스펙트럼을 기록하고 매개변수 A<를 추정했습니다. /나> =0.25의 현상식 Γ =Γ b +A v F /R , 여기서 Γ b 는 진공 상태의 은 구체에 대한 벌크 금속 이완 속도입니다. 먼저, 평균 직경이 〈D인 은 구체 빔에 대한 소멸 스펙트럼을 계산했습니다. 〉=2 nm 및 D 영역에 걸친 실험적 크기 분포 =1 ~ D =4nm. 우리의 이론에는 조정 가능한 매개변수가 없습니다. 유전 기능을 정의하기 위해 Lynch와 Hunter[16]가 제안한 벌크 은의 굴절률 표를 사용했습니다(그림 1 참조). 우리는 또한 Eqs를 적용했습니다. (16), (21), (22) ω p =9.17 eV, Γ b =0.021 eV, v F =1.39×10 6 m/s 및 A =0.25. 계산 결과 및 실험 스펙트럼은 그림 2에 나와 있습니다.
<그림>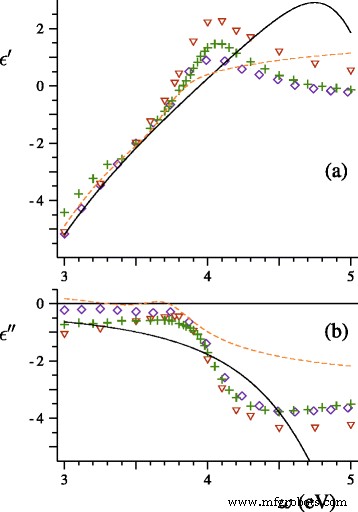
실제(a ) 및 가상(b ) Johnson and Christy(◇)[20], Lynch and Hunter(+)[16], Weber(△)[21], Hao and Nordlander(파선 ) [22], 그리고 Drachev et al. (실선 ) [23]
<사진>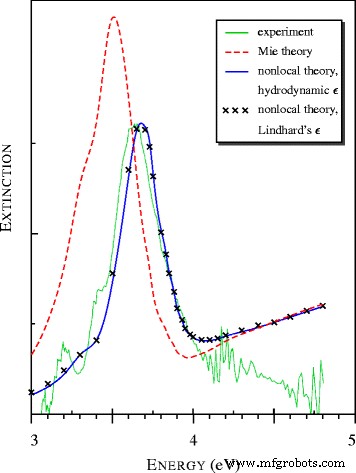
[15]에서 관찰된 은 나노미터 크기 입자에 의한 광소광 스펙트럼. 국부 및 비국부 모델로 계산. 모든 이론적 스펙트럼은 공통 상대 단위로 표시됩니다.
그림 2의 이론적 스펙트럼은 Klimontovich-Silin-Lindhard와 훨씬 단순한 유체역학적 유전 함수를 사용하여 계산되었습니다. |a |>플라즈몬 공명 영역에서 1.
나노미터 크기의 은 구체의 경우, Fröhlich[17], 플라즈몬 및 표면 플라즈몬 폴라리톤(SPP)[15] 공명이라고 하는 소멸 스펙트럼의 최대값은 3.5 eV에서 3.65 eV로 이동하는 것으로 알려져 있습니다[18]. 비국소 모델은 실험 데이터와 매우 잘 일치하는 반면, 로컬(Mie) 이론은 ω에서 최대값을 제공합니다. ≃3.5 eV(그림 2 및 표 1 참조).
플라즈몬 공명의 청색 편이의 계산은 다음 고려 사항에 의해 뒷받침될 수 있습니다. 정전기 근사에서 b 1 멸종 단면 Q에 기여 내선 및 식. (30)은 다음 근사를 사용하여 단순화할 수 있습니다.
$$ \frac{k_{2} R\,\psi_{l}^{\prime}(k_{2} R)}{\psi_{l}(k_{2} R)}\simeq l+1; \,\,\, \frac{k_{1} R\,\zeta_{l}^{\prime}(k_{1} R)}{\zeta_{l}(k_{1} R)} \simeq -\,엘. $$ (32)따라서 Q 내선 최대값은
입니다. $$ \Re [2\,(1+\delta_{1})\,\epsilon_{1}+ \epsilon_{2}]=0. $$ (33)얻어진 조건 (33)은 L의 여기를 고려합니다. 모드(δ라는 용어로 1 ) 따라서 Fröhlich 공명 조건[17]과 다릅니다.
$$ \Re (2\,\epsilon_{1}+ \epsilon_{2})=0. $$ (34)실험 [15]에서 피크 주파수 ω m 및 공진 폭 Δ ω 소멸 스펙트럼의 〈D 〉. Δ의 이 기능은 ω 고전적인 Mie 이론에 동의하지 않는 것 같습니다. 실제로 지역 이론은 D의 감소와 함께 플라즈몬 공명의 확장을 예측합니다. (A에서 =0.25) 표 1에 나와 있습니다. 동시에 nonlocal 이론은 공진 폭은 거의 같지만 피크 위치는 다릅니다. 모든 입자의 기여도를 중첩하면 Δ 값이 제공됩니다. ω 실험 데이터와 현저하게 일치합니다. 비국소 이론이 A에서도 빔의 플라즈몬 공명의 확대를 예측한다는 점은 흥미롭습니다. =0.
ω에서>4 eV에서 그림 2의 부드러운 이론적 곡선은 밀접하게 위치한 좁은 실험 피크의 매쉬보다 높습니다. 대역간 흡수는 그림 1에서 확인할 수 있는 것처럼 이 스펙트럼 범위에서 지배적입니다. 스펙트럼의 관찰된 특성은 연속체 대역에서 이산 레벨 구조로의 전환 결과일 가능성이 높습니다. 이러한 양자 크기 효과는 금 나노구의 광학적 특성 연구에서 일찍 발견되었다[19]. 은구의 크기를 〈D로 늘렸을 때 ≥3.5 nm에서 흡수는 먼저 최대값에 비해 증가하고 일련의 작은 등거리 딥과 함께 안정기를 형성했습니다. 그 후 〈D에서 흡수가 약간 감소했습니다. 〉=4 nm.
플라즈몬 공명의 블루윙 형성을 연구하기 위해 초주석 은 입자의 소광 스펙트럼을 계산하여 그림 3에 제시하였다. 그림 3에서 주목할 만한 특징은 <나>디 =1nm. 이전에 이 효과는 금 나노구에 대한 실험 연구에서 관찰되었습니다[19]. 특히, [19]의 그림 9에서는 1.7, 1.9, 2.0, 2.1, 2.3, 2.5 나노미터의 직경을 갖는 입자의 실험 스펙트럼을 국부 Mie 이론으로 계산된 스펙트럼과 비교하였다. 플라즈몬 공명의 확대와 그 위치를 설명하는 데 실패하여 합의가 좋지 않았습니다[19]. 입자의 크기를 변경하고 유전 기능을 수정하여 적합성을 개선하려는 시도는 연속적이지 않았습니다. [19]의 저자에 따르면 관찰된 비정상적으로 넓거나 움푹 들어간 집단 진동 대역은 지역 Mie 이론의 제안된 수정에 적합하지 않습니다. 그림 4에서 알 수 있듯이 nonlocal Mie 이론을 적용하면 상황이 극적으로 변한다. 조정 가능한 매개변수를 사용하지 않았습니다. Johnson과 Christy[20]에 의한 복합 굴절률의 표는 금의 유전 기능을 결정하는 데 사용되었습니다. A를 포함한 기타 매개변수 =1 및 톨루엔의 굴절률(1.37)은 [19]에서 가져왔습니다.
<그림>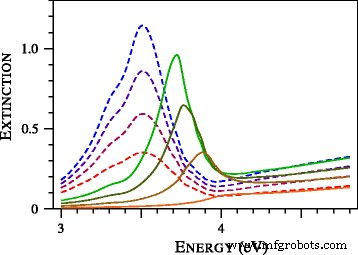
2.2, 1.8, 1.4 및 1.0nm의 직경을 가진 은 입자의 정규화된 소광 단면은 로컬(파선)로 계산됩니다. ) 및 비국소(실선 ) 미에 이론. 입자가 작을수록 곡선이 낮아집니다. 모든 이론적 단면은 공통 상대 단위로 표시됩니다.
<그림>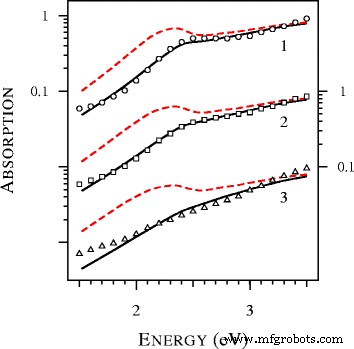
국부적으로 계산된 흡수 스펙트럼(점선 ) 및 비로컬(실선) ) 미에 이론 및 실험 데이터(도트) ) D가 있는 금 구체에 대해 [19]의 그림 9에서 추출 =2.5, 2.1, 톨루엔 1.7 nm(곡선 1 및 원 , 곡선 2 및 사각형 , 곡선 3 및 삼각형 , 각각). 모든 이론적 스펙트럼은 4.12 eV에서 1로 정규화되고 수직으로 변위됩니다.
세로 모드는 파수 값이 훨씬 더 높다는 점에서 가로 모드와 다릅니다. 예를 들어, 그림 2에 제시된 계산에서 \(k_{2}^{\mathrm {L}}\)의 실수 부분은 공간 주기 \(\Lambda =2 \pi /\Re k_{ 2}^{\mathrm {L}}\) ω에서 9nm에서 2nm로 감소 3에서 4 eV로 증가합니다. 이 ω에서 구간, 비율 \(k_{2}^{\mathrm {L}}/k_{2}\)의 절대값이 130에서 100으로 감소하고 매개변수 δ 식의 (27) θ에서 0.01에서 0.005로 감소 1 =π /4. 따라서 우리는 평평한 은 표면에서 L파의 여기가 무시될 수 있다고 결론지었습니다. 그러나 L 모드는 나노미터 크기의 은 클러스터에서 중요한 것으로 밝혀졌습니다.
식에서 \(-\,\omega ^{2}_{\mathrm {p}}/(\omega ^{2}+i \Gamma \omega)\) 용어의 대체. (16) ε 티 −ε g 식에 따라 (21) 분산 Eq.를 다시 쓸 수 있습니다. (15) 다음 형식
$$ 1+\frac{3}{5}\,a^{2}+\frac{3}{7}\,a^{4}+\frac{3}{9}\,a^{6 }+\dots=\frac{1}{1-\epsilon^{\mathrm{T}}/\epsilon_{\mathrm{g}}}. $$ (35)ε의 가장 간단한 경우 g =1 및 Γ =0, 식 (35) 금속은 ω에서 횡파와 L파 모두에 대해 투명하다고 예측합니다.>ω p 하지만 둘 다 k 엘 그리고 k 티 ω에서 복소수 <ω p .
고체가 투명하면 평면에 p편광파가 비스듬히 입사할 때 세로파가 여기될 수 있습니다. 이 효과에는 몇 가지 뚜렷한 특징이 있습니다. 첫째, 종파는 평평한 표면에서 생성될 수 있지만 표면 플라즈몬 폴라리톤을 여기시키려면 특별한 노력이 필요합니다[4, 5]. 둘째, 간섭 패턴에서 전자기장 강도는 계면을 따라가 아니라 수직으로 변조됩니다. 따라서 공극은 고체의 파쇄로 인해 표면과 평행한 평면에 나타날 수 있습니다. ω의 정의에 따르면 p , 조건 ω>ω p 전류 캐리어의 밀도가 낮은 고체(예:반도체)에서 충족될 수 있습니다. ε의 공식 때문에 여기서는 이 경우를 검토하지 않습니다. 엘 축퇴 전자 가스에 대해 파생되었습니다.
공간 의존적 유전 함수를 정의하기 위해 이전의 모든 연구자들은 평면 전자기파와 물질의 상호 작용을 고려했습니다. 이 접근 방식은 필드가 공동에 국한되어 있고 경계 조건을 어떻게든 고려해야 하는 경우 나노 광학에서 건설적이고 엄격하지 않습니다. 벡터 헬름홀츠 방정식을 만족하는 전기장에 대한 매질의 응답을 계산하여 이 문제를 해결했습니다. 파생된 공간 분산 유전 함수는 헬름홀츠 방정식의 매개변수인 파수의 제곱에 의존하지만 평면파의 파동 벡터에는 의존하지 않습니다.
금속에서 종파의 여기로 인해 수정된 프레넬 반사 계수를 보고합니다. 유사한 일반화가 Mie 계수에 대해 더 일찍 이루어졌습니다. 여기서, 나노미터 크기의 은과 금 클러스터에 의한 소광 시뮬레이션으로 이론을 검증하였다. 3.5에서 3.65 eV로 계산된 이동과 은 입자 빔의 표면 플라즈몬 공명의 폭은 실험 데이터와 매우 일치합니다. 또한, 비국소 모델은 직경이 약 2nm인 황금 구체의 플라즈몬 공명의 소멸을 설명합니다. It is important that L wave can be excited on a flat surface by a plane incident wave. This is the main difference of the plasmon polaritons from the surface plasmon polaritons.
The properties of the electromagnetic oscillations in metals have been examined. It has been found that the absolute values of the wavenumbers of the longitudinal waves are much larger than those of the transverse waves. For example, in silver at a photon energy of 3.5 eV, the ratio of the absolute values of the wavenumbers is equal to 130. There, the real part of the wavenumber of the longitudinal wave corresponds to a wavelength of 7 nm. The large difference in the wavenumbers prevents excitation of the L waves at a planar surface. However, the L modes have been shown to be excited in silver and gold nanometer-sized particles.
나노물질
초록 수직으로 정렬된 Si 나노와이어(Si NW)의 주기적으로 정렬된 어레이는 제어 가능한 직경과 길이로 성공적으로 제작되었습니다. 그들의 광전도 특성은 개별 나노와이어에 대한 광전도성 원자력 현미경(PCAFM)에 의해 조사됩니다. 결과는 Si NW의 광전류가 레이저 강도에 따라 크게 증가함을 보여주며, 이는 Si NW가 우수한 광전도성과 광응답 능력을 가짐을 나타냅니다. 이 광강화 컨덕턴스는 I-V 곡선 분석에 의해 확인된 광유도 쇼트키 장벽 변화에 기인할 수 있습니다. 한편, 정전기력현미경(electrostatic force
최근 강철은 Thomasnet.com 플랫폼에서 가장 많이 소싱된 제품 중 하나였습니다. 판금 및 금속 스탬핑 설비가 증가하고 있으며 이 시장의 성장에 기여하고 있습니다. 그러나 철강과 금속이 항공우주, 항공, 의료 산업의 중요한 공급원이라는 사실도 놀라운 일이 아닙니다. 오늘날 COVID-19의 세계적 대유행에 시의적절합니다. 그렇다면 철강 및 금속 제조 비즈니스는 어떻게 비즈니스 성장의 모멘텀을 계속 유지할 수 있습니까? 첫째, 명확한 사업 계획이 있는지 확인하십시오. 일부 제조업체는 가능한 모든 조치를 취하여 제조 비즈니스를