나노물질








스핀 및 밸리 축퇴가 모두 해제되는 주기적인 포텐셜에서 실리신의 스핀 및 밸리 종속 에너지 밴드와 수송 특성을 연구합니다. Dirac point, miniband, band gap, isotropic velocity, conductance는 스핀과 밸리 지수에 크게 의존함을 알 수 있다. 여분의 Dirac 포인트는 전압 전위가 증가함에 따라 나타나며, 스핀과 골이 다른 전자에 대해 임계값이 다릅니다. 흥미롭게도 갭리스 그래핀 이외의 전기장과 교환장으로 인해 속도가 크게 억제된다. 특정 계곡 부근의 특정 스핀에 대해 우수한 콜리메이션 효과를 얻을 수 있다. 스핀 및 밸리 종속 밴드 구조를 사용하여 전송을 조정할 수 있으며 Dirac 지점에서 완벽한 전송이 관찰됩니다. 따라서 구조적 매개변수에 의해 효과적으로 전환될 수 있는 현저한 스핀 및 밸리 분극이 달성됩니다. 중요한 것은 스핀과 밸리 분극이 주기적인 전위의 무질서에 의해 크게 향상된다는 것입니다.
<섹션 데이터-제목="배경">6각형 격자 구조를 갖는 2차원(2D) Dirac 재료는 silicene[1, 2], 전이 금속 dichalcogenides[3, 4] 및 phosphorene[5]와 같은 그래핀의 발견 이후 광범위하게 탐구되고 있습니다. 그래핀은 많은 특정 특성을 가지고 있지만 제로 밴드 갭과 약한 스핀-궤도 상호작용(SOI)으로 인해 응용이 제한됩니다. 최근에는 그래핀의 실리콘 유사체인 silicene이 에피택시 성장을 통해 제작되었으며[6-10], 이론적 연구에 의해 안정성이 예측되었다[11, 12]. 그래핀과 실리신은 K 주위에 유사한 밴드 구조를 가지고 있습니다. 및 K ′ 계곡과 둘 다의 저에너지 스펙트럼은 상대론적 Dirac 방정식[13]으로 설명됩니다. 그래핀과 달리 실리신은 강한 고유 SOI와 좌굴 구조를 가지고 있습니다. 강한 SOI는 Dirac 지점[13, 14]에서 틈을 열어 스핀과 밸리 자유도 사이의 결합으로 이어질 수 있습니다. 좌굴 구조는 실리신 시트에 수직인 외부 전기장에 의해 밴드 갭을 제어할 수 있게 해줍니다[14-16]. 또한, silicene은 기존의 실리콘 기반 전자 기술과 더 호환되는 장점이 있습니다. 이러한 특성으로 인해 실리신은 차세대 나노전자공학을 위한 우수한 재료입니다. 특히, 실온에서 실리신 전계 효과 트랜지스터는 실험[17]에서 성장-전달-가공 공정에 의해 성공적으로 제작되었다.
2D Dirac 재료의 발견은 계곡의 양자 제어를 탐구하는 새로운 기회를 제공합니다. 동등하지 않은 두 계곡 K 및 K ′ 첫 번째 Brillouin 영역에서 양자 정보 및 양자 계산을 위한 전하 및 스핀 외에 추가 자유도로 간주될 수 있습니다[18-20]. 예를 들어, 전자 스핀 큐비트를 스핀-밸리 큐비트로 확장하기 위해 밸리 자유도를 통합할 수 있습니다[18]. 따라서 Valley pseudospin을 생성, 감지 및 조작하는 것을 목표로 하는 Valleytronics가 상당한 관심을 끌고 있습니다. 그래핀에서 고유한 에지 모드[21, 22], 삼각 휨 효과[23], 토폴로지 라인 결함[24, 25], 변형률[26, 27] 및 정전기 게이트를 활용하여 밸리 분극을 달성하기 위한 다양한 방식이 제안되었습니다. [28]. 그래핀에 비해 실리신은 계곡 슈도스핀 연구에서 상당한 이점이 있다. silicene은 다양한 외부 필드의 변조 하에서 다양한 위상 위상과 Chern 수를 나타내는 것으로 밝혀졌습니다[13, 16, 29, 30]. 전기장이 있는 경우 E z 및 교환 필드 h , Ezawa는 E z -어 스핀 및 밸리 인덱스가 특징인 평면 [16]. Rashba SOI를 추가로 고려하면 토폴로지 상전이로 인해 밸리 편광된 양자 비정상 홀 상태가 silicene에서 예측됩니다[31]. 상태 전이를 기반으로 약 100% 스핀 분극을 갖는 실리신 기반 스핀 필터가 제안되어 약한 무질서에 대해 강건합니다[32]. Yokoyama는 강자성(FM) 규소 접합을 통한 탄도 수송을 연구하고 제어 가능한 스핀 및 밸리 분극 전류를 시연했습니다[33]. 반전 대칭이 깨진 전이 금속 디칼코게나이드에서 고유 SOI에서 발생하는 가전자대의 스핀 분할은 시간 반전 대칭으로 인해 두 골에서 반대입니다[3, 34, 35]. 깨진 반전 대칭은 K 또는 K ′ 각각 오른쪽 또는 왼쪽 원형 편광을 통한 계곡 [3, 34]. 실험에서 밸리 편광의 신호는 광학 [36, 37] 및 전송 [38, 39] 측정에 의해 조사되었습니다. 대칭 파괴 게이트 전기장을 받은 이중층 그래핀에서 거대한 비국소 밸리 홀 효과가 관찰되었으며, 비국소 신호는 실온까지 지속됩니다[38]. 2D Dirac 재료의 Valleytronics에 대한 최근 리뷰는 Ref. [40].
초격자는 반도체 및 2D 재료에서 전자 구조를 엔지니어링하는 효과적인 방법입니다[41]. 나노크기의 초격자 패턴은 그래핀이나 실리신이 금속 기판 위에 놓일 때 실험에서 자연적으로 발생할 수 있습니다[42, 43]. 그래핀의 초격자는 실험적으로 관찰된 키랄 특성으로 인해 스펙트럼에서 새로운 Dirac 점의 생성과 등방성 페르미 속도[44]의 재정규화로 이어질 수 있습니다[43, 48, 49]. 전기장이 있는 규소 초격자 E z 및 교환 필드 h , 스핀 및 밸리 축퇴가 모두 해제됩니다. 초격자에 의한 미니밴드 구조와 미니갭은 스핀과 밸리 지수에 의존하는 것으로 확인되었다[50]. 게다가, 스핀 및 밸리 분극은 실리신 초격자에 의해 향상될 수 있다[51]. 그래핀과 마찬가지로 규소 초격자에서도 많은 새로운 전자 구조가 예상됩니다. 그러나 규소 초격자에 대한 연구는 매우 적습니다[50, 51]. 이 논문에서 우리는 보완적인 측면, 즉 스핀 및 밸리 종속 밴드 구조와 실리신의 수송 특성에 대해 자세히 논의합니다. 우리는 스핀과 밸리 지수가 구조적 매개변수에 의해 조정될 수 있는 추가 디랙 포인트와 이방성 속도에 서로 다른 영향을 미친다는 것을 발견했습니다. 전기장과 교환장으로 인해 속도가 크게 억제됩니다. 이 장애에 의해 크게 향상될 수 있는 현저한 스핀 및 밸리 분극이 달성됩니다.
논문은 다음과 같이 구성되어 있습니다. "방법" 섹션에서는 이론적 형식주의와 분산 관계를 제시합니다. 밴드 구조, 스핀 및 밸리 편광 전송에 대한 수치 결과는 "결과 및 논의" 섹션에 나와 있습니다. 마지막으로 "결론" 섹션의 요약으로 마무리합니다.
단일 입자 근사에서 Dirac 점 근처의 silicene 전자 구조는 효과적인 Dirac Hamiltonian을 따릅니다. 고려 중인 시스템은 일련의 국소 전위 장벽 U에 의해 형성된 1차원 규소 초격자입니다. , 필드 교환 h , 수직 전기장 E z . 유 , h , 및 E z 장벽 너비가 d인 장벽 영역에만 존재합니다. b , 반면 U =h =이 z 웰 너비가 d인 웰 영역에서 =0 와 , 그림 1에 표시된 대로. Kronig-Penney 유형의 초격자는 x를 따라서만 변합니다. 방향이며 한 단위의 길이는 d입니다. =d b +d 와 . 유사한 모델이 Refs에서 논의되었습니다. [51, 52], 본 연구에서 연구된 밴드 구조와 무질서 효과보다는 주로 열전 및 전자 수송에 초점을 맞춘다. 실험적으로 U 금속 게이트 및 h에 의해 생성될 수 있습니다. 실리신 층 위에 주기적으로 증착되는 FM 절연체 EuO[33]의 자기 근접 효과에 의해 생성될 수 있습니다(그림 1 참조). 전기장 E z silicene에 수직으로 적용하면 엇갈린 하위 격자 전위 Δ를 유도할 수 있습니다. z =ℓ 이 z , 2ℓ ≈0.46Å A의 수직 분리 그리고 B 좌굴 구조로 인한 두 하위 격자의 사이트 [16]. 따라서 전자 상태는 Hamiltonian,
에 의해 설명될 수 있습니다. $$\begin{array}{@{}rcl@{}} H =\hbar v_{F} (k_{x} \tau_{x} - \eta k_{y} \tau_{y}) + \Delta_ {\eta \sigma} \tau_{z} + U_{\sigma}. \end{array} $$ (1) <그림>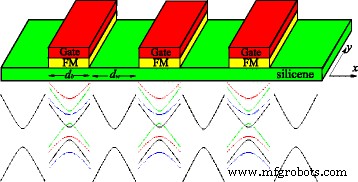
위:규소 초격자의 개략도. silicene 상부에 있는 EuO 및 EuS와 같은 FM 절연체는 그래핀에 대해 제안된 바와 같이 silicene에서 교환 장을 유도한다[53]. FM 절연체 상단의 금속 게이트는 로컬에서 페르미 레벨을 제어합니다. 하단:외부 필드가 있거나 없는 규소의 에너지 스펙트럼 개략도
Δ η σ =Δ z −η σ λ 그래서 엇갈린 전위 Δ로 제어할 수 있는 다양한 스핀 및 밸리 지수에 대한 밴드 갭을 설명합니다. z 및 SOI λ 그래서 . 유 σ =우 −σ 어 는 다양한 스핀 지수에 대한 효과적인 잠재력입니다. η =±1은 K를 나타냅니다. 및 K ′ 계곡. σ =±1은 스핀업 및 스핀다운 상태를 나타냅니다. v F 는 페르미 속도입니다. silicene에서 내부 및 외부 Rashba 효과는 매우 작으며 무시할 수 있습니다[15].
y에 따른 번역 불변성으로 인해 방향, 횡파 벡터 k 와 보존됩니다. 계곡 η에 대한 파동 함수 그리고 스핀 σ 각 지역의 형식은 Ψ입니다. (x ,y )=ψ (x )e 아이키 와
$$\begin{array}{@{}rcl@{}} \psi(x) =A \left(\begin{array}{cc} 1 \\ \frac{\hbar v_{F} k_{-} }{\epsilon_{\eta \sigma}} \end{array}\right) e^{i q_{\eta \sigma} x} + B \left(\begin{array}{cc} 1 \\ \frac {- \hbar v_{F} k_{+}}{\epsilon_{\eta \sigma}} \end{array}\right) e^{-i q_{\eta \sigma} x}. \end{배열} $$ (2)장벽 지역에서는 ε η σ =ε b =(이 -유 σ )+Δ η σ 그리고 x 파동 벡터의 성분 \( q_{\eta \sigma } =q_{b} =\sqrt {(E - U_{\sigma })^{2} - \Delta ^{2}_{\eta \sigma } - (\hbar v_{F} k_{y})^{2}} / \hbar v_{F} \). 우물 영역에서 ε η σ =ε 와 =이 −η σ λ 그래서 및 \( q_{\eta \sigma } =q_{w} =\sqrt {E^{2} - \lambda _{SO}^{2} - (\hbar v_{F} k_{y})^{ 2}} / \hbar v_{F} \). ㅋ ± =q η σ ±나 η ㅋ 와 . 전송 확률 T η σ 전송 행렬 기법을 사용하여 계산할 수 있습니다. 0 온도에서 특정 계곡의 특정 스핀에 대한 정규화된 컨덕턴스는
$$\begin{array}{@{}rcl@{}} G_{\eta \sigma} (E) =\frac{1}{2} \int_{-\pi/2}^{\pi/2 } T_{\eta \sigma} (E,E\sin \theta) \cos \theta d \theta, \end{array} $$ (3)여기서 θ x에 대한 입사각입니다. 방향. 스핀 및 계곡 분해 컨덕턴스는 \(G_{\uparrow (\downarrow)} =\left (G_{K \uparrow (\downarrow)} + G_{K^{\prime } \uparrow (\downarrow )} \right) / 2 \) 및 \(G_{K (K^{\prime })} =\left (G_{K (K^{\prime }) \uparrow } + G_{K (K^{ \prime }) \downarrow } \right) / 2\), 각각. 그런 다음 스핀 분극 P를 소개합니다. s 및 계곡 편파 P v :
$$\begin{array}{@{}rcl@{}} P_{s} =(G_{\uparrow} - G_{\downarrow}) / (G_{\uparrow} + G_{\downarrow}), \ 끝{배열} $$ (4) $$\begin{배열}{@{}rcl@{}} P_{v} =(G_{K} - G_{K^{\prime}}) / (G_{ K} + G_{K^{\prime}}). \end{배열} $$ (5)Bloch의 정리와 파동 함수의 연속성 조건에 기초하여 분산 관계 E (카 x ) K 근처의 스핀업 및 스핀다운 전자의 경우 및 K ′ 계곡을 계산할 수 있습니다.
$$ \begin{정렬} \cos(k_{x} d) &=\cos(q_{w} d_{w}) \cos(q_{b} d_{b}) \\&\quad- \frac {(\epsilon_{b} q_{w})^{2} + (\epsilon_{w} q_{b})^{2} + (\epsilon_{b} \!- \!\epsilon_{w}) ^{2} k^{2}_{y}}{2 \epsilon_{w} \epsilon_{b} q_{w} q_{b}} \sin(q_{w} d_{w}) \sin( q_{b} d_{b}), \end{정렬} $$ (6)그리고 k x 는 Bloch 파수입니다. 계산을 단순화하기 위해 무차원 단위가 도입되었습니다. \(E \rightarrow E d / \hbar v_{F}\), \(U \rightarrow U d / \hbar v_{F}\), \(\ 람다 _{SO} \rightarrow \lambda _{SO} d / \hbar v_{F}\), \(\Delta _{z} \rightarrow \Delta _{z} d / \hbar v_{F}\) , \(h \rightarrow hd / \hbar v_{F}\), k 와 →ㅋ 와 d , 카 x →ㅋ x d , d 와 →d 와 /d , 및 d b →d b /d . Δ에서 z =λ 그래서 =h =0, 식 (6) 스핀과 밸리가 모두 퇴화되는 주기적인 포텐셜에서 틈이 없는 그래핀에서 발견되는 것으로 환원된다[44-47]. 식에서 (6) 교환 필드 h를 볼 수 있습니다. 계곡이 축퇴를 유지하는 동안 단독으로 스핀의 분할을 유발할 수 있습니다. 그러나 계곡 축퇴는 전기장 E에 의해 해제될 수 있습니다. z SOI λ의 도움으로 그래서 . 따라서 교환장과 전기장의 조합은 그림 1과 같이 스핀 및 밸리 축퇴를 들어올릴 수 있습니다[16, 31-33]. 제안된 시스템에서 다른 밸리 근처에서 다른 스핀을 가진 전자는 다양한 밴드를 나타냅니다. 구조 및 운송 기능.
이 섹션에서는 위의 방정식을 사용하여 실리신 초격자에서 서로 다른 스핀 및 밸리 인덱스에 대한 밴드 구조 및 전송 속성을 계산합니다. 장벽과 우물의 너비는 다음과 같다고 가정합니다. 우물과 장벽 너비가 같지 않은 경우의 결과(d b ≠d 와 ) 갭리스 그래핀의 것과 유사하다[47]. 일부 매개변수는 d로 설정됩니다. b =d 와 =50 nm 및 λ 그래서 달리 명시되지 않는 한 =3.9 meV(실리신). 우리는 페르미 준위 근처의 처음 두 개의 미니밴드(가장 낮은 원자가 및 전도 미니밴드)에 집중할 것입니다.
첫째, 잠재 U의 효과 에너지 밴드의 gapless 경우와 gapless 경우를 동시에 논의하기 위해 Δ를 설정했습니다. z =7.8 meV=2λ 그래서 . 잠재력이 없는 경우(U =0), K 근처의 스핀업 전자 계곡(K ↑ 전자) 및 K 근처의 스핀다운 전자 ′ 계곡(K ′ ↓ 전자)는 갭이 없는 반면(그림 2(a1, a4) 참조) 스핀다운 전자는 K 근처에 있습니다. 계곡(K ↓ 전자) 및 K 근처의 스핀업 전자 ′ 계곡(K ′ ↑ 전자)에는 큰 간격이 있습니다(그림 2(a2, a3) 참조). 스핀업(또는 스핀다운) 전자의 미니밴드는 E에서 음(또는 양) 에너지 범위로 이동합니다. =0 by h , 효과적인 잠재력으로 인해 U σ =우 −σ 어 . K의 밴드 구조 ↑ (또는 K ↓ ) 전자 및 K ′ ↓ (또는 K ′ ↑ ) E에 대한 전자 존재 거울 대칭 =0, 식과 일치 (6). 그러나 이 거울 대칭은 U가 있으면 파괴됩니다. . U 증가하면 추가 Dirac 포인트가 나타나며 그 동안 그 수가 증가합니다. 여분의 Dirac 점은 주변에 있는 파동 함수의 키랄성에 의해 입증될 수 있습니다[46]. 실리신 시스템에서 Dirac 포인트의 특징은 그림 2와 같이 스핀 및 밸리 자유도에 크게 의존합니다. 예를 들어 U에서 K에 대한 그림 2(d1–d4)의 =135 meV ↑ , 케이 ↓ , 케이 ′ ↑ 및 K ′ ↓ 전자의 경우 Dirac 포인트의 수는 각각 5, 6, 4 및 7입니다. U의 특정 값에 대해 , 예:U =40.66 meV for K ↓ 전자(그림 2(b2) 참조) 및 U =100.63 meV for K ′ ↑ 전자(그림 2(c3) 참조), 새로운 Dirac 포인트는 k에서 생성될 수 있습니다. 와 =0이고 k에서 반대 방향으로 이동하는 쌍으로 분할됩니다. 와 =0점이지만 항상 k를 유지 x =0, U 추가 증가합니다. 결과적으로 K의 밴드 갭은 ↓ 및 K ′ ↑ 전자가 닫히고(그림 2(b2, c3) 참조), 갭이 있는 시스템은 갭이 없게 됩니다. U의 임계값을 찾기 위해 , 우리는 d를 설정했습니다. b =d 와 그리고 k x =0. 갭리스 그래핀의 규칙과 유사하게 [47], 암시적 함수 정리를 고려하면 새로운 Dirac 점에서 세로 파동 벡터가 q를 만족한다는 결론을 내릴 수 있습니다. b =q 와 언제
$$\begin{array}{@{}rcl@{}} E_{0} =\frac{(U - \sigma h)^{2} - \Delta_{z}^{2} + 2 \eta \ 시그마 \Delta_{z} \lambda_{SO}}{2(U - \sigma h)}. \end{array} $$ (7) <그림>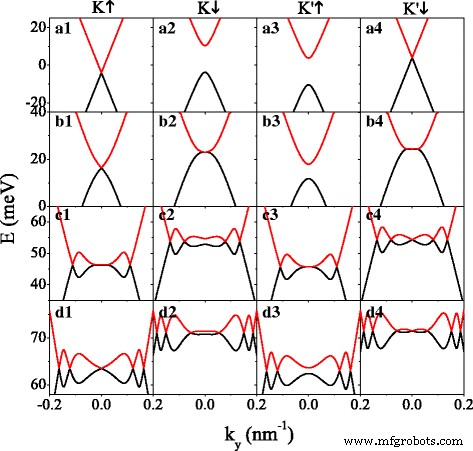
에너지 스펙트럼 대 k 와 잠재적 U의 여러 다른 값에 대해 . (a1–a4) U =0; (b1–b4) U =40.66 meV; (c1–c4) U =100.63 meV; (d1–d4) U =135.0 meV. 매개변수의 값은 h입니다. =8.0 meV, Δ z =7.8 meV 및 k x =0
K를 위해 ↑ 및 K ′ ↓ η를 갖는 전자 σ =1, Δ일 때 z =2λ 그래서 , 식 (7)
로 줄일 수 있습니다. $$\begin{array}{@{}rcl@{}} E_{0} =\frac{U - \sigma h}{2}. \end{배열} $$ (8)이에 따라 식. (6)
로 바뀝니다. $$ {}\cos^{2}(q_{w} d_{w}) - \frac{\left(\epsilon_{b}^{2} + \epsilon_{w}^{2}\right) q_ {w}^{2} + (\epsilon_{b} - \epsilon_{w})^{2} k^{2}_{y}}{2 \epsilon_{w} \epsilon_{b} q_{w }^{2}} \sin^{2}(q_{w} d_{w}) =1, $$(9)\(\left (\epsilon _{b}^{2} + \epsilon _{w}^{2}\right) q_{w}^{2} + (\epsilon _{b} - \epsilon _{w})^{2} k^{2}_{y} =-2 \epsilon _{w} \epsilon _{b} q_{w}^{2}\) 또는 q 와 d =2n π (n 양의 정수임). 식을 기반으로 합니다. (8), 우리는 ε b =−ε 와 , 따라서 이전 평등은 k인 경우에만 충족됩니다. 와 0 K의 경우 =0 ↑ 및 K ′ ↓ Δ의 전자 z =2λ 그래서 , 원래 Dirac 점에 해당합니다. q 솔루션 와 d =2n π
형식을 가짐 $$\begin{array}{@{}rcl@{}} k_{y0} =\pm \frac{1}{d} \sqrt{\frac{\left(E_{0}^{2}-\ 람다_{SO}^{2}\right)d^{2}}{(\hbar v_{F})^{2}} - (2n\pi)^{2}}. \end{배열} $$ (10)\(\sqrt {E_{0}^{2}-\lambda _{SO}^{2}}d / 2\pi \hbar v_{F} \geq n\)일 때, k 와 0 실제이며 (E에 정확히 위치한 새로운 Dirac 포인트가 발생합니다. 0 ,카 와 0 ). U의 낮은 값에서 , 카 와 0 가상이며 n에 대한 솔루션이 없습니다. , 이는 추가 디랙 포인트가 없음을 의미합니다. Dirac 포인트는 U의 임계값 이후에만 나타납니다. , 예:U =40.66 meV for K ↓ n에 해당하는 그림 2(b2)의 전자 =1. 식에 따르면 (10), 디랙 포인트 수 N 디 얻어 질 수있는. Δ일 때 z =2λ 그래서 ,
$$\begin{array}{@{}rcl@{}} N_{D} =2 \left[ \frac{\sqrt{E_{0}^{2}-\lambda_{SO}^{2}} d}{2\pi\hbar v_{F}} \right] + 1 \end{배열} $$ (11)K를 위해 ↑ 및 K ′ ↓ 전자, 동안
$$\begin{array}{@{}rcl@{}} N_{D} =2 \left[ \frac{\sqrt{E_{0}^{2}-\lambda_{SO}^{2}} d}{2\pi\hbar v_{F}} \right] \end{배열} $$ (12)K를 위해 ↓ 및 K ′ ↑ 여기서 [...]는 정수 부분을 나타냅니다. U의 임계값에서 , 예:U =40.66 meV 및 100.63 meV, Dirac 포인트 수는 N입니다. 디 =2n K의 경우 -1 ↓ 및 K ′ ↑ 전자(그림 2(b2, c3) 참조).
식 (7)과 (10)은 Dirac 포인트의 위치와 수가 전기장 E에 의해 조정될 수 있음을 나타냅니다. z 및 교환 필드 h . 그림 3은 Dirac 포인트 수 N을 보여줍니다. 디 U의 함수로 E의 다른 값에 대해 z 그리고 h . Δ일 때 z 그림 3a에서 =7.8 meV, U 증가 , N 디 K를 위해 ↑ 및 K ′ ↓ 전자는 Eq와 일치하여 홀수의 형태로 증가합니다. (11). 아니 디 K를 위해 ↓ 및 K ′ ↑ 전자는 Eq와 일치하여 짝수의 형태로 증가합니다. (12), N 제외 디 임계값에서. 그림 3a와 b를 비교하면 h 증가하면 스핀다운(또는 스핀업) 전자의 임계값이 점차 감소(또는 증가)합니다. Δ일 때 z =15 meV≠2λ 그래서 그림 3c에서 N 디 N을 제외한 모든 전자에 대해 짝수의 형태로 증가합니다. 디 임계값에서. U의 중요한 가치는 스핀과 골이 다른 전자의 경우 다릅니다. Dirac 포인트는 매개변수 U의 공동 변조로 제어할 수 있습니다. , E z , 및 h .
<사진>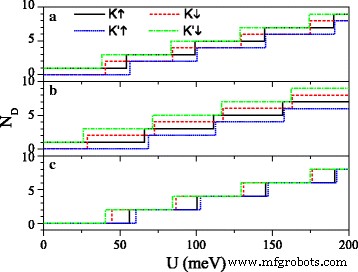
디랙 포인트 수 N 디 잠재 U 대 . (아 ) h =8.0 meV 및 Δ z =7.8 meV; (b ) h =20.0 meV 및 Δ z =7.8 meV; (ㄷ ) h =8.0 meV 및 Δ z =15.0 meV
잠재적인 U 및 장벽 너비 d b 그림 4와 같이 밴드 갭을 조절하는 데 사용할 수 있습니다. K의 갭 ↑ 및 K ′ ↓ 전자는 작지만 K의 간격은 ↓ 및 K ′ ↑ 전자는 Δ로 인해 큽니다. η σ =Δ z −η σ λ 그래서 . U로 증가하면 모든 미니밴드가 점차 고에너지 영역으로 이동하고(그림 4a 참조) 모든 밴드 갭은 U로 감쇠 진동을 표시합니다. (그림 4b 참조). U일 때 =σ 어 , 유효 전위는 0이고 갭은 최대값에 도달합니다. 격차는 U의 임계값에서 닫힙니다. , 새로운 Dirac 포인트의 출현으로 인해. 그림 4c, d는 장벽 너비 d에 대한 미니밴드 및 밴드 갭의 의존성을 나타냅니다. b U에서 =0. 외부 필드가 없는 경우(d b =0), 미니밴드는 계속 퇴화하고 페르미 레벨의 갭은 2λ입니다. 그래서 . d의 등장으로 b , 밸리와 스핀이 비축퇴되는 미니밴드가 분할됩니다. K의 미니밴드 ↑ (또는 K ↓ ) 및 K ′ ↓ (또는 K ′ ↑ ) 전자는 E에 대해 거울 대칭을 유지합니다. =0(그림 4c 참조). d b K의 갭이 증가합니다. ↓ 및 K ′ ↑ 전자는 점차 넓어집니다. K의 갭 ↑ 및 K ′ ↓ 전자는 d일 때 0으로 감소합니다. b d 만족 b /d 와 =λ 그래서 /Δ z , 이후 d로 증가 b (그림 4d 참조). d의 추가 증가와 함께 갭 너비가 포화에 접근합니다. b . 또한, 미니밴드의 너비는 d로 좁혀집니다. b 고유 상태의 더 적은 결합으로 인해 증가합니다(그림에는 표시되지 않음). 밴드 갭에 대한 전기장의 영향은 이전 연구[50]와 유사합니다.
<그림>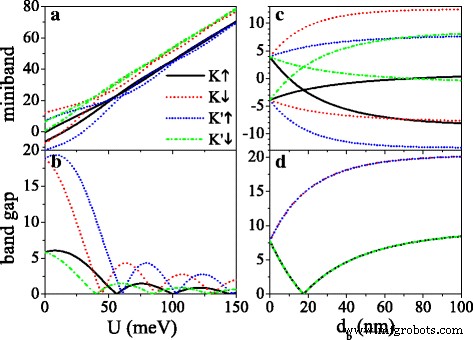
(아 ) 페르미 레벨 근처의 미니밴드 및 (b ) 원래 Dirac 지점 대 잠재적인 U에서의 밴드 갭 , d에 b =d 와 =50nm. (ㄷ ) 페르미 레벨 근처의 미니밴드 및 (d ) 원래 Dirac 지점 대 d에서의 밴드 갭 b , U에서 =0 및 d 와 =50nm. 다른 매개변수의 값은 h입니다. =8.0 meV, Δ z =15.0 meV 및 k x =카 와 =0
그룹 속도는 그림 5와 같이 스핀 및 밸리 지수에 크게 의존합니다. 구성 요소(v x ,v 와 )의 속도는
로 정의할 수 있습니다. $$\begin{array}{@{}rcl@{}} v_{x} / v_{F} =\partial E / \partial k_{x}, \quad v_{y} / v_{F} =\ 부분 E / \부분 k_{y}. \end{array} $$ (13) <그림>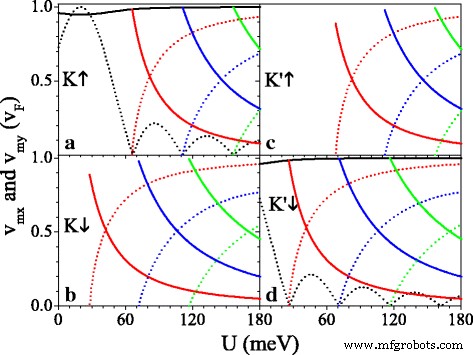
(아 –d ) 속도 대 잠재력 U , 매개변수는 h로 설정됩니다. =20.0 meV 및 Δ z =7.8 meV. 검정, 빨강, 파랑 및 녹색 실선 곡선은 속도 v입니다. 0x , v 1x , v 2x , 및 v 3x , 각각. 검정, 빨강, 파랑 및 녹색 점선 곡선은 속도 v입니다. 0y , v 1y , v 2y , 및 v 3y , 각각
그림 5는 속도 구성요소 v를 나타냅니다. mx 및 v 나의 v 단위 F 원래 Dirac 지점(m =0) 및 새로운 Dirac 포인트(m) =1,2,3). U로 볼 수 있습니다. 증가, v 0y 감쇠 방식으로 진동하고 v 0x ≈v F 거의 영향을 받지 않습니다(그림 5a, d 참조). U의 임계값에서 새로운 Dirac 포인트가 나타나는 곳, v mx ≈v F 하지만 v 0y =v 나의 =0, k를 따라 시준 동작을 나타냅니다. x 특정 스핀 및 밸리에 대한 방향. U일 때 임계값을 초과하고 추가로 증가합니다. v 나의 v로 증가 F 하지만 v mx 점차적으로 0으로 감소합니다. 주기적 전위의 효과는 키랄 특성의 결과로 매우 이방성입니다. 이방성 속도의 특징은 간격 Δ으로 인해 스핀과 밸리에 따라 다양합니다. η σ 잠재적인 U σ , U를 사용하여 명령할 수 있습니다. . U 복용 =20 meV(예:v) 0y =v F K를 위해 ↑ 전자는 v보다 훨씬 큽니다. 0y =0.16v F K를 위해 ′ ↓ 전자, v 없음 0y K를 위해 ↓ 및 K ′ ↑ 밴드갭으로 인한 전자. v mx (또는 v 나의 ) 스핀업 전자의 경우 동일한 밸리에 있는 스핀다운 전자의 경우보다 항상 더 크거나 작습니다. 특히 그림 5는 U의 작은 값에 대해 , v 0x , v 0y , 및 v mx v보다 작습니다. F Δ로 인해 z 그리고 h , 갭리스 시스템 이외 [44]. 예를 들어, v 1x =0.98v F , 0.89v F , 0.89v F 및 0.98v F K를 위해 ↑ , 케이 ↓ , 케이 ′ ↑ 및 K ′ ↓ Dirac 점이 나타날 때 각각 전자. Δ의 영향력을 밝히기 위해 z 그리고 h 그룹 속도에서 그림 6은 속도(v 0x ,v 0y ) (a) Δ의 함수 z 및 (b) h K를 위해 ↑ 전자. 그림 6a에서 v 0x Δ로 단조 감소 z 동안 v 0y Δ의 변화에 둔감합니다. z . 반대로, v 0x h에 둔감하다 , 동안 v 0y 최대값 v으로 증가 0y =v F h에 =σ 유 그런 다음 h로 감소합니다. . 결과는 그룹 속도가 Δ에 의해 억제될 수 있음을 나타냅니다. z 그리고 h 실리신에서.
<그림>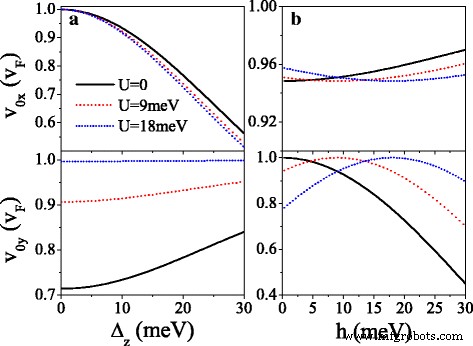
속도 v 0x 및 v 0y 대 (a ) Δ z 그리고 (b ) h , K용 ↑ 전자. (아 ) h =20.0 meV 및 λ 그래서 =Δ z /2. (b ) Δ z =7.8 meV
스핀 및 밸리 종속 밴드 구조는 전송 속성에 반영되며 전송 제어에 대한 지침을 제공합니다. 이 섹션에서 우리는 유한 규소 초격자를 통한 스핀 및 밸리 편극 수송의 특성에 대해 논의합니다. 그림 7은 전송 확률 T를 보여줍니다. η σ (a, c) K ↑ 및 (b, d) K ↓ 전자 및 주기 수 n =10. 빨간색 점선 곡선은 전송을 결정하는 다양한 전자 상태의 경계이기도 한 미니밴드입니다. 미니밴드 영역에서는 전송이 제한되고 밴드 갭 영역에서는 전송이 되지 않는 것을 볼 수 있습니다(그림 7a, b 참조). 전송 분포는 k를 중심으로 대칭입니다. 와 =0은 대칭 미니밴드로 인한 것입니다. 전송의 공진 특성은 공진 상태에서 발생합니다. 전송은 k 근처의 갭 영역에 여전히 존재한다는 점에 유의해야 합니다. 와 =0은 고유 상태의 터널 효과로 인한 것입니다. 티 η σ K에 대한 페르미 수준에서 ↑ 및 K ↓ 전자는 각각 그림 7c, d)에 나와 있습니다. T를 사용하여 많은 얇은 공진 피크를 명확하게 볼 수 있습니다. η σ =1은 Dirac 포인트의 위치에서 정확하게 발생하여 시스템을 스핀 및 밸리 필터로 적용할 수 있음을 시사합니다.
<그림>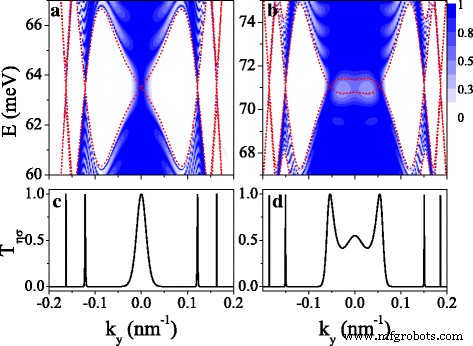
전송 T의 등고선 플롯 η σ (이 ,카 와 ) (a) ), (ㄷ ) 케이 ↑ 전자 및 (b ), (d ) 케이 ↓ 전자. 매개변수의 값은 그림 2(d1–d4)와 동일하며 n =10
스핀 및 밸리 인덱스에 대한 밴드 구조의 강한 의존성은 높은 스핀 및 밸리 분극의 실현에 유리합니다. 그림 8은 미니밴드, 컨덕턴스 G를 나타냅니다. η σ , 스핀 분극 P s , 및 계곡 편파 P v 잠재적 U의 함수로 . It can be found that the distribution of conductance is completely in agreement with the band structure, that is, the conductance (or conductance gap) corresponds to the miniband (or band gap). The minibands for spin-up and spin-down electrons could be alternative distribution by adjusting h 제대로. Consequently, \(G_{K(K^{\prime })\uparrow }\) and \(G_{K(K^{\prime })\downarrow }\) present alternative distribution as well, i.e., \(G_{K(K^{\prime })\uparrow }\) nearly vanishes for those regions where \(G_{K(K^{\prime })\downarrow }\) is in resonance and vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ z , the minibands and conductances for electrons near K and K ′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.
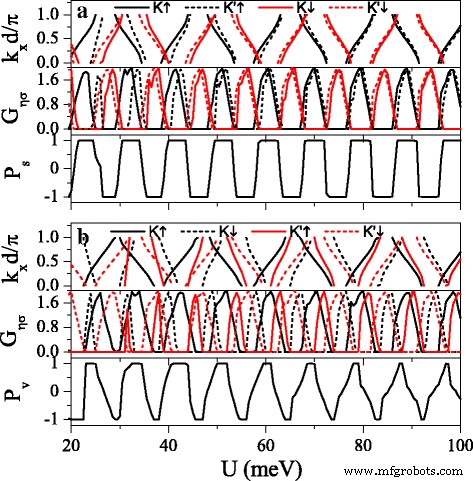
Minibands, conductances G η σ , spin polarization P s , and valley polarization P v versus potential U . (아 ) Δ z =4.0 meV. (b ) Δ z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d b =d 와 =120 nm, and n =10
Figure 9 shows the (a) spin polarization P s and (b) valley polarization P v in (U ,h ) space. Interestingly, both P s and P v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P s and P v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U 그리고 h . For example, when h =6 meV and U =42 meV, P s ≈1 and P v ≈1, meaning that the current is mainly contributed by K ↑ electrons. When h =6 meV and U =44 meV, P s ≈1 and P v ≈−1 while P s ≈−1 and P v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.
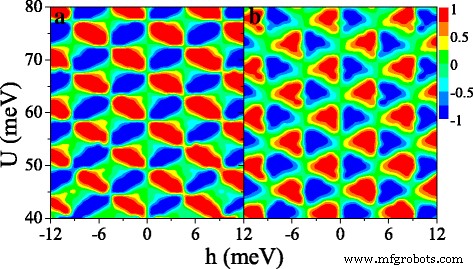
Contour plot of (a ) spin polarization P s (U ,h ) 및 (b ) valley polarization P v (U ,h ), at Δ z =10.0 meV. The values of other parameters are the same as these in Fig. 8
In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ z 그리고 h fluctuate around their mean values, given by 〈Δ z 〉=Δ z 0 and 〈h 〉=h 0 , 각각. The fluctuations are given by
$$\begin{array}{@{}rcl@{}} \Delta_{z} |_{i} =\Delta_{z0} (1 + \delta \zeta_{i}), \quad h |_{i} =h_{0} (1 + \delta \zeta_{i}), \end{array} $$ (14)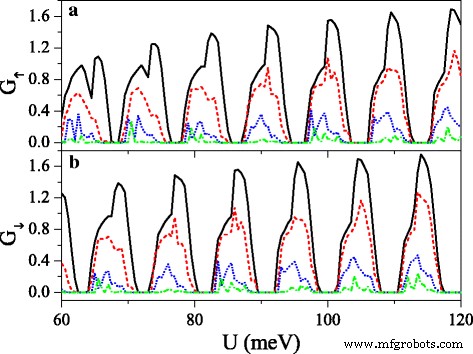
Conductances (a ) G ↑ and (b ) G ↓ versus potential U , when the electric field presents disorder, at n =50 and Δ z 0 =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8
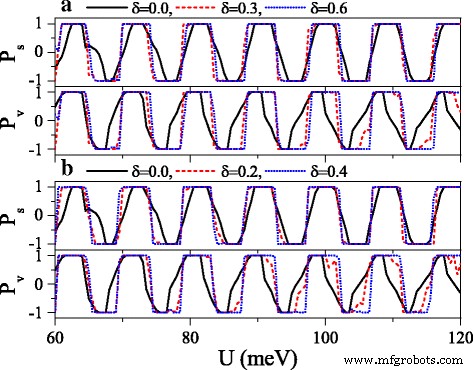
Polarizations P s and P v versus potential U when a the electric field or b the exchange field presents disorder. Δ z 0 =20.0 meV and h =7.0 meV in (a ). Δ z =20.0 meV and h 0 =7.0 meV in (b ). The values of other parameters are the same as these in Fig. 10
where {ζ 나 } is a set of uncorrelated random variables or white noise, − 1<ζ 나 <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y direction. Thus, k 와 still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G ↑ and (b) G ↓ . With the presence and increase of the disorder strength δ , both G ↑ and G ↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G ↑ completely fall into the forbidden (or allowable) ranges of G ↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G 케이 and G 케이 ′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P s and P v . Obviously, with the increase of δ , P s and P v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.
In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.
2차원
Ferromagnetic
Spin-orbit interaction
나노물질
초록 실현 가능한 밴드 구조 엔지니어링 및 그에 따른 향상된 발광 효율을 실현하기 위해 InGaNBi는 가시광선 및 중적외선의 광자 장치에 활용될 수 있는 매력적인 합금입니다. 본 연구에서는 밴드갭, 스핀 궤도 분할 에너지, InGaNBi 대 In 및 Bi 조성의 기판 변형과 같은 구조적, 전자적 특성을 1차 원리 계산을 사용하여 연구합니다. 격자 매개변수는 In 및 Bi 조성이 증가함에 따라 거의 선형으로 증가합니다. 비스무트 도핑에 의해 4차 InGaNBi 밴드갭은 0.38-1.9μm의 파장 범위에 해당하는 최대 9.375%의
초록 제어 가능한 광학 속성은 광전자 응용 분야에 중요합니다. 2차원 Janus WSSe의 고유한 특성과 잠재적인 응용을 기반으로 첫 번째 원칙 계산을 통해 WSSe 이중층의 변형률 변조된 전자 및 광학 특성을 체계적으로 조사합니다. 선호되는 적층 구성 및 칼코겐 차수는 결합 에너지에 의해 결정됩니다. 모든 안정적인 구조의 밴드갭은 외부 응력에 민감한 것으로 밝혀졌으며 적절한 압축 변형 하에서 반도체에서 금속성에 맞춰질 수 있습니다. 원자 궤도 투영 에너지 밴드는 축퇴와 구조적 대칭 사이의 양의 상관 관계를 보여주며, 이는 밴드갭