나노물질








나노결정 앙상블의 발광 역학은 균일하지 않은 확장된 샘플 및 입자간 상호작용에서 복사 및 비방사 속도의 크기 의존성을 포함하여 다양한 프로세스에 의해 복잡합니다. 이는 실리콘 나노결정(SiNC)의 특정 경우에 대해 Kohlrausch 또는 "신장된 지수"(SE) 기능으로 널리 모델링된 비지수적 붕괴를 초래합니다. 우리는 먼저 exp[− (t /τ) β ]. 그런 다음 발광 감쇠 또는 모집단 감쇠가 이 함수를 따른다고 가정하여 계산된 분포와 평균 시간을 비교하고 결과가 β에 대해 유의하게 다르다는 것을 보여줍니다. 1보다 훨씬 낮습니다. 그런 다음 이 두 가지 유형의 SE 기능과 다른 모델을 평균 크기가 다른 두 개의 열 성장 SiNC 샘플의 발광 감쇠 데이터에 적용합니다. 평균 수명은 실험 설정 및 선택한 피팅 모델에 크게 의존하며, 어느 것도 앙상블 붕괴 역학을 적절하게 설명하는 것으로 보이지 않습니다. 그런 다음 수명 분포를 직접 추출하기 위해 주파수 분해 분광법(FRS) 기술이 SiNC에 적용됩니다. 비율 분포는 ~ 0.5 디케이드의 절반 너비를 가지며 주로 다소 고주파수 편향된 로그 정규 함수와 유사합니다. TRS와 FRS 방법의 조합은 광범위한 방출 스펙트럼을 갖는 NC 재료의 발광 역학을 밝히는 데 가장 적합합니다.
콜로이드 나노 입자는 촉매 작용, 의료 치료 및 광전자 응용을 포함한 다양한 응용 분야에서 사용될 수 있습니다[1,2,3,4]. 반도체 나노 입자는 발광, 광전지 및 광촉매 응용 분야에서 특히 중요합니다[5, 6]. 실리콘 나노결정(SiNC)은 조정 가능한 방출 특성[7]과 실리콘의 풍부함 및 생체 적합성[8]으로 인해 현재 관심의 초점입니다. 나노입자 기반 기술을 개발하려면 관련 광전자 특성에 대한 깊은 지식이 필요하며 시간 분해 분광법은 종종 이러한 목적에 유용한 도구입니다.
SiNC의 발광 수명은 일반적으로 기본 형식 exp[ − (λt)를 갖는 확장 지수(SE) 함수로 모델링됩니다. ) β ], 여기서 분산 매개변수 β 0과 1 사이의 값을 취합니다. λ 는 비율 매개변수이고 t 시간이다. 이 함수는 종종 "지수보다 느림"으로 설명되며 더 긴 수명으로 이어지는 붕괴 속도의 비대칭 분포를 의미합니다. 일단 β 및 λ 매개변수가 발광 감쇠 곡선을 피팅하여 발견된 경우 해당 감쇠율 분포를 대략적으로 재구성할 수 있습니다[9].
실리콘 및 기타 반도체 양자점에서 SE 발광 감쇠의 기원은 지난 20년 동안 크게 논의되었으며 최근에도 논쟁이 계속되고 있습니다[10]. 붕괴 역학에서 SE의 출현에 대한 다양한 설명이 제안되었는데, 여기에는 캐리어 터널링 및 나노결정의 밀접하게 이격된 앙상블에서의 트래핑[11], 비균질하게 넓어진 크기 분포[12], 크기 의존적 전자-포논 커플링[10]이 포함됩니다. , 그리고 비방사성 재결합을 위한 장벽 높이의 분포[13], 후자는 다공성 실리콘에 대한 이전 제안과 유사합니다[14]. 분명히, 속도 분포에 대한 지식은 보다 일반적으로 반도체 나노결정뿐만 아니라 SiNC의 발광 메커니즘을 이해하는 데 필요합니다.
SiNC에 대한 많은 이전 문헌에서 확장된 지수 붕괴는 일반적으로 다른 가능한 분포에 대한 분석 없이 선험적으로 가정되었습니다. SE는 시각적으로 잘 맞는 경향이 있습니다(즉, 가장 잘 맞는 선이 "눈으로" 데이터와 잘 일치하는 것으로 나타남). 더욱이 [15]와 같은 대부분의 이전 작업에서 인구 감소 또는 발광 감소가 실제로 모델링되는지에 대한 명확성이 부족합니다. 이것들은 도함수에 의해 관련되며 샘플의 붕괴 시간 척도를 이해하려면 올바른 표현을 사용해야 합니다[16]. 또한 검출기의 반응성 함수는 넓은 앙상블 방출 스펙트럼으로 인해 SiNC에서 측정된 발광 감쇠 곡선에 상당한 영향을 미칠 수 있습니다. 그럼에도 불구하고 반응성을 고려한 경우가 거의 없어 여러 조사의 결과를 비교하기가 어렵습니다. 마지막으로, 이전 연구에서는 실리콘 나노결정의 분석에 주파수 분해 분광법(FRS)을 사용하려고 시도한 적이 없습니다. 원칙적으로 FRS는 모델을 선험적으로 가정하지 않고 수명 분포를 추출하는 것을 허용합니다.
이 논문의 목적은 실리콘 나노결정의 발광 역학을 측정, 모델링 및 해석하는 접근 방식을 확립하는 것입니다. 이것이 문헌에서 종종 모순되는 결과의 광대한 다양성을 더 잘 이해하는 데 도움이 될 수 있고, 다른 측정 간에 더 나은 일치 또는 적어도 더 일관성을 이끌어내고, 발광 메커니즘을 더 잘 이해하는 데 도움이 될 수 있기를 바랍니다.
Si 나노결정에 널리 사용되는 신장 지수(stretched exponential), 최근 SiNC에 처음 적용된 대수 정규 붕괴 분포[17], 이분자 붕괴의 세 가지 모델을 비교합니다. 모든 모델에 대해 강도 함수 g의 적분으로 표시되는 방출 확률 밀도 함수 (그 ), 시간 t' t'에 남아 있는 여기의 비율과 관련이 있습니다. [16]에 따라.
$$ {\int}_0^tg\left({t}^{\hbox{'}}\right) dt=1-\frac{c_t}{c_0}, $$ (1)여기서 c 그 및 c 0 t 시간에 들뜬 NC의 수입니다. 그리고 처음에는. 확률 밀도 함수는 시간 0과 t 사이에 방출된 광자의 비율을 나타냅니다. 방출된 광자의 총 수에 비례합니다. 인구 감소가 1차 비율 방정식(즉, "단분자" 재조합)을 따르는 경우 dc 그 /dt = − λc 그 , 여기서 λ =1/τ 0 , 일반적인 c 그 /ㄷ 0 =exp[− λt ] 및 g (그 ) =λ⋅ exp[− λt ] 식의 양변에 시간 미분을 취한 후 1. dt' 창에서 측정된 발광 강도 때문에 미분이 필요합니다. 해당 구간에 대한 들뜬 부분의 변화에 비례합니다.
복사율과 비방사성 비율을 모두 고려하면 총 감쇠율 λ을 대체합니다. λ R + λ NR 그래서 g (그 ) =(λ R + λ NR )exp[− (λ R + λ NR 그 ] =λ R exp[− (λ 리 + λ NR )그 ] + λ NR exp[− (λ R + λ NR )그 ] 여기서 첫 번째 항만 측정 가능하며,
$$ g(t)={\lambda}_R\exp \left[-\left({\lambda}_R+{\lambda}_{NR}\right)t\right]. $$ (2)데이터를 피팅하는 데 사용되는 감쇠 함수, I 그 =아· exp(− λt ) + dc, 추가 임의의 전인자, A로 확장 이는 검출 효율과 여기된 나노입자의 수에 따라 달라지며 적절한 규모로 이어질 것입니다. DC 오프셋은 일반적으로 다른 피팅 매개변수로 감쇠 기능에 추가됩니다.
확장된 지수 감쇠의 경우 여기된 방출기의 비율은 다음과 같이 감쇠합니다.
$$ \frac{c_t}{c_0}=\exp \left[-{\left({\lambda}_{SE}t\right)}^{\beta}\right]. $$ (3)여기서 λ SE 확장된 지수 감쇠율입니다(1/τ와 동일). SE ). 이것을 식에 대입하면 1 및 이전과 같이 양변의 미분을 취하면 다음과 같이 주어진 방출 확률 함수가 생성됩니다.
$$ g(t)={\beta \lambda}_{SE}^{\beta }{t}^{\beta -1}\exp \left[-{\left({\lambda}_{SE} t\right)}^{\beta}\right]. $$ (4)주파수 분포를 추정하는 방법 H (λ ) 식으로 이어진다. 3은 역 라플라스 변환[9]을 사용하여 표시되어 β가 감소함에 따라 넓어지는 분포를 생성합니다. 고주파 쪽으로 치우쳐 있습니다.
불행히도, Eq. 4, prefactor를 복사 부분과 비 복사 부분으로 분리하는 것은 불가능합니다. 이것은 Eq. 4는 λ에 대해서만 올바르게 정규화됩니다. NR = 0[16]이며, PL 감쇠 곡선에서 얻은 수명 분포는 이러한 방식으로만 이해됩니다. 또한 전인자에 시간 종속 항이 있습니다. 따라서 집단 붕괴는 발광 붕괴와 비교하여 다른 시간 의존성을 갖는다[16, 18]. τ 값을 얻으려면 SE 및 β 적절한 평균 수명을 추출할 수 있는 인구 감소에 대해 Eq를 사용해야 합니다. 4 관찰된 붕괴를 모델링하기 위해 여기서 g를 대체합니다. (그 ) 측정된 감쇠 함수 I 그 :
$$ {I}_t=A{\beta \lambda}_{SE}^{\beta }{t}^{\beta -1}\exp \left[-{\left({\lambda}_{SE }t\right)}^{\beta}\right]+\mathrm{dc}. $$ (5)식에서 5, 스케일링 매개변수(β도 흡수할 수 있음) 및 λ prefactor의 용어) 및 dc 오프셋이 피팅 매개변수로 삽입되었습니다. 평균 수명은 다음과 같습니다.
$$ \left\langle {\tau}_{SE}\right\rangle =\frac{\tau_{SE}}{\beta}\Gamma \left[\frac{1}{\beta}\right], $$ (6)여기서 Γ 감마 함수를 나타내며 평균 감쇠 시간은
$$ \left\langle t\right\rangle ={\tau}_{SE}\frac{\Gamma \left(2/\beta \right)}{\Gamma \left(1/\beta \right)} . $$ (7)많은 이전 작업에서 "표준" 확장 지수 exp[− (λ SE 그 ) β ] 인구 감쇠 대신 발광 감쇠를 모델링합니다. 따라서 다음과 같이 정규화된 강도 함수가 있습니다.
$$ g(t)=\frac{\lambda_{SE}\beta }{\Gamma \left(1/\beta \right)}\exp \left[-{\left({\lambda}_{SE} t\right)}^{\beta}\right]. $$ (8)방정식 8은 t =0이고 ∞는 1과 같습니다. 해당 피팅 모델은 간단히
$$ {I}_t=A\exp \left[-{\left({\lambda}_{SE}t\right)}^{\beta}\right]+\mathrm{dc}. $$ (9)식 9는 (식 4와 같이) 식 4와 같은 사실에도 불구하고 널리 적용되고 종종 SiNC 발광 데이터에 아주 잘 맞습니다. 8은 100%의 절대 양자 효율(AQY)에 대해 엄격하게 정규화됩니다. 종종 간과되는 점은 τ를 추출할 수 없다는 사실입니다. SE (=1/λ SE ) 및 β 식에 의해 모델링된 발광 감쇠로부터 9를 사용하여 Eqs로 평균 시간을 계산합니다. 6 및 7. 본질적으로 Eqs. 4와 8은 서로 다른 강도 붕괴 모델이며 다른 인구 붕괴 함수, 평균 시간 및 붕괴 속도 분포를 예상해야 합니다.
식에 의해 주어진 강도 함수로 이어질 인구 감소를 찾기 위해. 9, 우리는 식에서 얻은 것과 동일한 프로세스를 적용합니다. 4에서 식. 5, 하지만 그 반대는 다음과 같습니다.
$$ \frac{c_t}{c_0}=1-\frac{\lambda_{SE}\beta }{\Gamma \left(1/\beta \right)}{\int}_0^t\exp \left[ -{\left({\lambda}_{SE}t\right)}^{\beta}\right]\cdot \mathrm{dt}. $$ (10)여러 단계 후에 Eq. 10은
$$ \frac{c_t}{c_0}=\frac{1}{\Gamma \left(1/\beta \right)}\Gamma \left[1/\beta, {\left({\lambda}_{ SE}t\right)}^{\beta}\right]. $$ (11)방정식 11은 Eq에 의해 주어진 강도 감쇠에서 얻은 인구 감쇠입니다. 8. 일반적인 방법으로 평균 수명을 찾으면
$$ \left\langle {\tau}_{SE}\right\rangle ={\tau}_{SE}\frac{\Gamma \left(2/\beta \right)}{\Gamma \left(1 /\베타 \오른쪽)} $$ (12)의 평균 붕괴 시간
$$ \left\langle t\right\rangle ={\tau}_{SE}\frac{\Gamma \left(3/B\right)}{2\Gamma \left(2/\beta \right)} . $$ (13)마지막으로 빈도 분포는 (1 /λ )·H (λ ), 여기서 이전과 같이 H (λ )는 ref에서 계산된 분포입니다. [9] 식에 의해 주어진 인구 감소에 대해. 3. 이러한 결과는 표 1에 요약되어 있습니다.
두 SE 공식 간의 차이는 중요합니다(그림 1). 문헌에서 강도 감쇠가 A· exp[− (t /τ SE ) β ] + dc (즉, Eq. 9) 그리고 평균 시간은 Eqs를 사용하여 계산됩니다. 6과 7. 이것은 수학적으로 잘못된 것처럼 보입니다. Eqs. 6과 7은 식에 의해 주어진 강도 감쇠에서 파생됩니다. 4, 방정식이 아닙니다. 8. 예를 들어, τ SE =100μs 및 β =0.7, 그림 1과 같이 exp[− (t)로 주어진 강도 감쇠에 대해 /τ SE ) β ], 식을 사용하여 127μs에 비해 199μs(식 12)의 평균 시간 상수를 찾습니다. 6. 평균 붕괴 시간에 대해서도 유사한 차이가 발견되었습니다(식 7 및 13). 또한 특성 수명을 추정하기 위한 Higashi-Kastner 방법[19]으로 알려진 접근 방식이 있는데, 이는 SE 붕괴 모델을 적용하는 대안으로 SiNC에 적용되었습니다[20, 21]. 이 모델에서 특성 지연 시간 t d , 단순히 I로 표시된 감쇠 데이터의 피크로 간주됩니다. 그 ·t 대 t . 이것은 (1 /β ) 1 /β ·τ SE 식에서 얻은 9 [20].
<그림>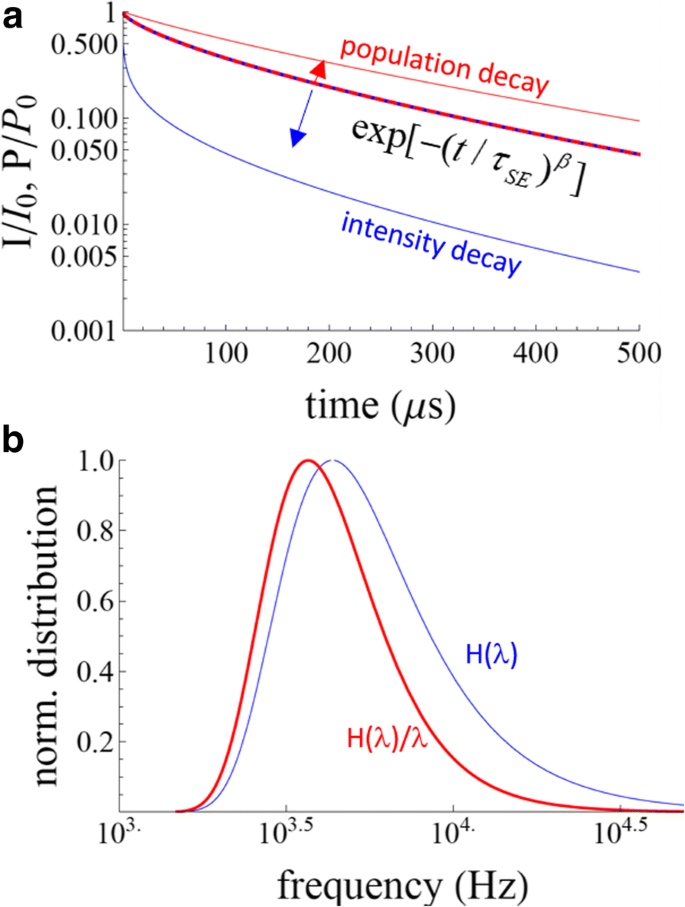
늘어난 지수. 아 τ 확장 지수 함수에 대한 인구 및 강도 감소 SE =100μs 및 β =0.7. 파란색-빨간색 점선은 exp[−입니다. (λt ) β ]. 이것이 인구 감소를 나타내는 경우 강도 감소는 파란색 선으로 표시됩니다. 만약 exp[− (λt ) β ]는 강도 감소이고, 인구 감소는 빨간색 선으로 표시됩니다. ㄴ 해당 비율 분포
대안적으로, 붕괴율의 분포는 특정 Η를 따를 수 있습니다. (λ ), 다음과 같이 주어진 발광 감쇠로 이어집니다.
$$ g(t)={\int}_0^{\infty}\mathrm{H}\left(\lambda \right)\cdot \exp \left(-\lambda t\right)\mathrm{d}\ 람다, $$ (14)여기서 Η (λ )는 감쇠율의 주파수 종속 분포를 나타냅니다. 방정식 14는 Eq.로 축소됩니다. Η인 경우 2 (λ )는 디랙 델타 함수 δ와 같습니다. (λ − λ 0 ) 또는 선택된 분포에 의해 가중치가 부여된 연속적인 지수 시리즈를 나타낼 수 있습니다. 많은 나노결정 앙상블이 자연적으로 대수정규 크기 분포를 따르기 때문에 대수정규 함수는 나노결정 시스템에서 합리적인 선택으로 보입니다[22]. 더 이상의 혼동을 피하기 위해 다음과 같이 주어진 대수 정규화 함수의 표준 정규화 정의를 사용합니다.
$$ H\left(\lambda \right)=\frac{1}{\lambda}\cdot \frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{\ 왼쪽(\ln \lambda -\mu \right)}^2}{2{\sigma}^2}\right]. $$ (15)측정된 감쇠 함수는
$$ {I}_t=A\cdot {\int}_0^{\infty}\left(\frac{1}{\lambda}\cdot \frac{1}{\sigma \sqrt{2\pi }} \exp \left[-\frac{{\left(\ln \lambda -\mu \right)}^2}{2{\sigma}^2}\right]\cdot \exp \left(-\lambda t \right) d\lambda \right)+ dc. $$ (16)SE 함수와 마찬가지로 두 개의 독립 변수(오프셋 및 배율 인수 포함)만 있습니다. 순간은 평소와 같이 정의됩니다. 즉, 중간 비율은 exp로 제공됩니다. (μ ), exp의 평균 (μ + σ 2 /2), 그리고 가장 가능성 있는 수명(분포의 정점)은 exp입니다. (μ − σ 2 ). 이전에는 비표준 분포가 사용되었습니다[16](즉, 자체적으로는 유효하지만 일반적으로 허용되는 로그 정규 분포 함수가 아닌 분포). 방정식 14는 복사 감쇠 분포에도 적용됩니다(즉, AQY =100%). 사실, 붕괴율 분포는 (알려지지 않은) 양자 효율 함수에 의해 가중된다는 것이 제안되었습니다[16]. 실제 상황에서는 표본에서 비복사율의 인구 분포를 아는 것이 어렵거나 불가능하다는 점을 감안할 때 이 경고를 받아들이기만 하면 됩니다.
발광 붕괴는 2차 반응(즉, "이분자" 붕괴)에 해당할 수도 있습니다[23]. 여기서 인구 감소 속도는 dc로 표시됩니다. /dt =− λ [ㄷ 그 ] 2 , 나머지 분수 c를 산출합니다. 그 /ㄷ 0 =(c 0 λt + 1) −1 . 이 식을 Eq.에 대입합니다. 1은 거듭제곱 법칙 붕괴를 초래합니다.
$$ {I}_t/{I}_0=A\frac{\lambda {c}_0}{{\left(\lambda {c}_0+1\right)}^2}. $$ (17)이분자 모델에는 하나의 속도 상수 λ만 있습니다. (비율 분포가 있는 확장 지수 및 로그 정규와 달리) 평균 수명이 없습니다. 보다 구체적으로, 시간 적분은 발산하고 2차 감쇠의 평균 수명은 무한합니다.
"표준" SE 기능(식 9)은 지금까지 SiNC 발광 감쇠에 사용되는 지배적인 모델이었으며 발광 메커니즘에 대한 감쇠의 의미를 해석하는 데 많은 논문이 사용되었습니다. 대수 정규 수명 분포는 아주 최근에 SiNC에 처음 적용되었습니다[17, 24, 25]. 분명히 어떤 모델을 가정할 선험적 이유가 거의 없으며 대신 붕괴율의 분포를 직접 설정하는 것이 더 좋습니다. 이것은 원칙적으로 최소한 SiNC가 아닌 비정질 실리콘에 여러 번 적용된 QFRS(Quadrature Frequency-Resolved Spectroscopy)에 의해 달성될 수 있습니다.
QFRS 방법은 희토류가 도핑된 유리[26,27 및 a-SiOx:H
직교 FRS 신호는 단일 지수 감쇠가 QFRS 스펙트럼에서 델타 함수를 생성하지 않는다는 사실로 인해 복잡합니다. 관찰된 신호는 실제로 [31]에 의해 로그 척도에 주어진 단일 지수 응답 함수를 가진 수명 분포의 컨볼루션입니다.
$$ {S}_{\log_{10}\mathrm{r}}=\frac{{\omega \tau}_0}{1+{\omega}^2{\tau}_0^2}, $$ (18)여기서 시간 상수 τ 0 =ω 0 −1 . 따라서 Decay rate 분포가 수십 년 폭이 아닌 한 의미 있는 분포를 추출하기 위해 deconvolution을 수행해야 합니다.
SiNC와 관련된 낮은 대비와 비정질 탄소 지지체의 겹치는 얼룩으로 인해 명시야 이미지를 사용하는 컴퓨터 기반 입자 계수 알고리즘을 적용할 수 없으며 픽셀 계수 소프트웨어를 사용하여 "눈으로" 직경을 추정해야 했습니다. 샘플 명시야 TEM 이미지는 그림 2a, d에 표시되어 있으며 수동 입자 계수 결과는 2.9 nm의 선형 평균 직경(평균 및 표준 편차의 자연 로그 μ =1.057 및 σ =0.1555) 및 5.4nm(μ =1.663 및 σ =0.1917), 각각 1100 및 1200 °C 어닐링 온도에 대해. 이러한 샘플은 이후 "작은" 및 "대형" SiNC라고 합니다. 크기는 선택된 NC(그림 2b, e)의 고해상도 이미징으로 추가로 확인되었으며, 여기서 격자 무늬는 NC를 식별하고 직경을 추정하는 또 다른 방법으로 사용될 수 있습니다. 푸리에 변환 적외선(FTIR) 분광법 및 XPS 데이터는 준비된 SiNC가 도데센으로 성공적으로 기능화되었음을 보여주었습니다. 그러나 작은 SiNC는 큰 것보다 더 산화되어 더 작은 정도의 기능화를 나타냅니다(추가 파일 1:그림 S1 및 S2).
<사진>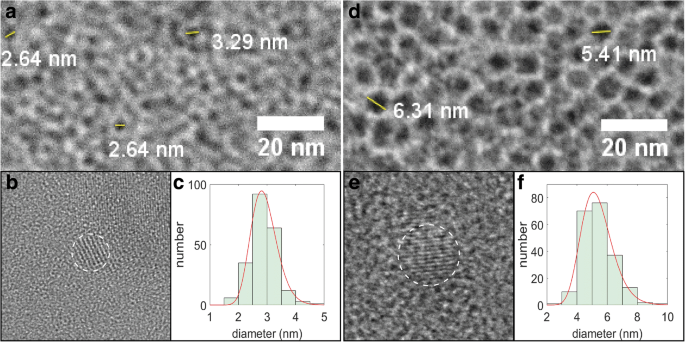
SiNC의 TEM 이미지. 아 명시야, b 고해상도 및 c 작은 SiNC에 대한 크기 분포 히스토그램. 패널 d –f 대형 SiNC의 유사한 이미지 세트를 나타냅니다.
광발광(PL) 스펙트럼은 660 및 825nm에 중심을 두고 있으며 작은 SiNC 및 큰 SiNC에 대해 각각 반치폭 최대값이 123 및 198nm입니다(그림 3 삽입). 간접 밴드갭 에너지는 \( {E}_g\kern0.5em =\kern0.5em \sqrt{E_{g,\mathrm{bulk}}^2\kern0.5em +\ kern0.5em D/{R}^2} \) [32] D 포함 =4.8eV 2 /nm 2 및 R 작은 입자에 대해서는 거의 일치하지만 큰 입자에 대한 PL 피크에서 얻은 것보다 약간 작은 밴드갭을 예측하는 NC 반경입니다. AQY는 작은 SiNC 샘플의 경우 12%, 큰 NC의 경우 56%였습니다. 다른 시스템에 대한 독립적인 측정은 두 샘플에 대해 18% 및 48%를 산출했으며, 이는 다른 여기 및 차단 파장에 대한 AQY 측정[33]의 불확실성의 전형입니다. 우리는 더 큰 NC의 덜 구부러지고 에너지가 낮은 표면이 더 나은 표면 기능화를 유도하고 비방사 표면 상태가 전체 PL 스펙트럼에 더 적은 기여를 한다고 가정합니다.
<그림>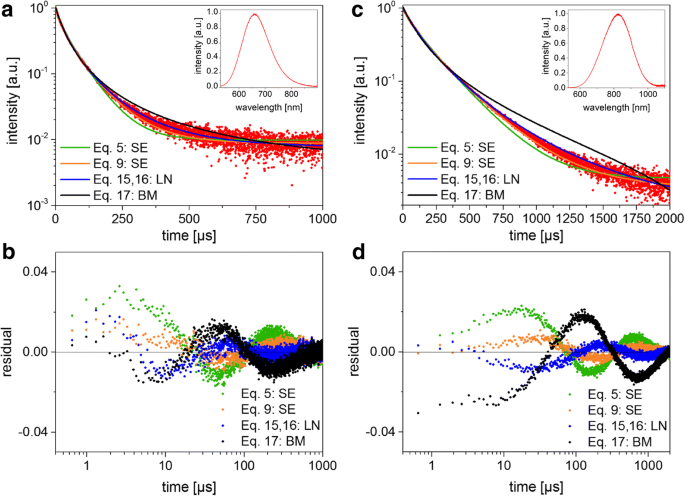
TRS 데이터 및 피팅 결과. 아 발광 감쇠 및 해당 피팅 기능(BM 이분자, SE 확장 지수, LN lognormal) 작은 SiNC의 경우. PL 스펙트럼은 삽입에 표시됩니다. ㄴ 적합에 대한 잔차 도표(a , ㄷ , d ) 큰 SiNC에 대한 곡선과 잔차를 보여줍니다.
두 샘플 모두 SiNC에 대한 광범위한 이전 문헌을 기반으로 예상한 대로 비지수적 붕괴를 산출했습니다. 측정된 PL 감쇠는 Eqs에 적합했습니다. 표준 제곱합 최소화를 사용하여 다양한 모델을 테스트하기 위해 5, 9, 16 및 17을 참조하십시오(그림 3). 넓은 NC 발광 스펙트럼에서 검출기의 반응성이 일정하지 않다는 사실은 나중에 논의될 것입니다. 모든 경우에 잔차가 진동하여 어떤 모델도 완전히 적절하지 않은 것처럼 보이지만 "단순한" SE 모델(식 9)과 로그 정규(식 16)는 잔차의 가장 낮은 제곱합을 향하는 경향이 있습니다. 두 SiNC 샘플에 대해 계산된 피팅 매개변수와 평균 수명이 표 2에 나와 있으며, 여기서 평균은 붕괴 모델의 선택에 따라 크게 달라집니다. Higashi-Kastner 방법도 적용되었으며(그림 4) 지연 시간 곡선을 치우친 가우시안으로 피팅하여 피크 위치를 결정했습니다. Higashi-Kastner 방법은 시간 상수 t를 산출합니다. d (1 /β ) 1 /β ∙τ SE , 이러한 값은 Eq.에서 가져옵니다. 9 [20] 이전에 표시된 대로. 이분자 모델은 지나치게 들뜨지 않는 분리된 나노결정과 일치하여 상당히 잘 맞지 않습니다. 따라서 더 이상 논의되지 않습니다.
<그림>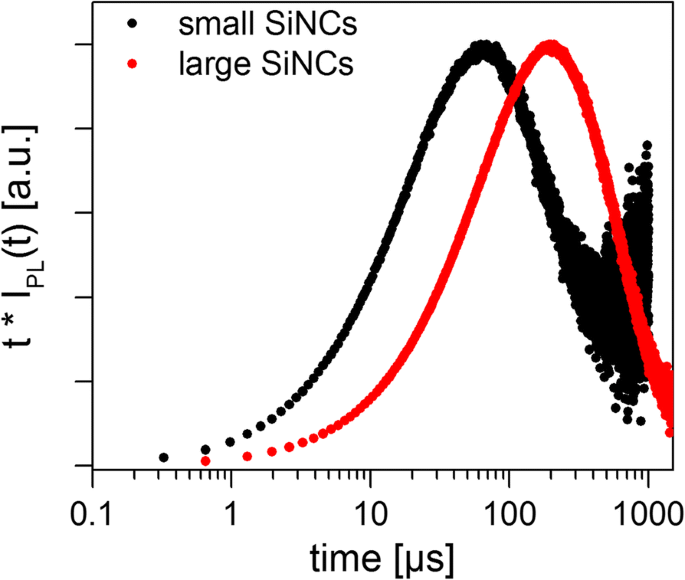
소형 및 대형 SiNC 앙상블에 대한 감쇠 시간(Higashi-Kastner 플롯)을 곱한 정규화된 PL 감쇠 곡선. 피크 위치는 t로 표시되는 가장 지배적인 감쇠 시간을 나타냅니다. d 표 2
이러한 측정 조건에 대해 평균적으로 NC당 여기자 수를 추정하려면 여기율을 흡수 단면적에서 계산해야 하며, 이는 분명히 10 −14 만큼 높을 수 있습니다. cm 2 이 실험을 위해 [34]. 4500 W/m 2 의 여기 복사 조도가 주어졌을 때 352 nm 및 측정된 피크 방출 속도(다음 섹션 참조)에서 크고 작은 SiNC에 대한 NC당 여기 수는 각각 ~ 1 및 0.2 미만인 것으로 추정되었습니다. 이것은 큰 SiNC가 약간 과도하게 흥분될 수 있음을 시사합니다. 이것은 일부 NC에 다중 여기자의 존재로 인해 추가적인 비방사 효과를 유발할 수 있습니다. 이 가능성을 더 평가하기 위해 수명을 가진 전력의 함수로 측정했습니다. 위에 보고된 값의 2%까지 감소합니다. 결과는 경향이 없었고 항상 ~ 2% 내에서 동일했습니다(추가 파일 1 그림 S3). 이는 저전력 측정에서 낮은 신호 대 잡음비에도 불구하고 피팅 및 반복성 오류에 가깝습니다. 따라서 NC의 가능한 과 여기가 결과에 거의 영향을 미치지 않는 것으로 보입니다.
TRS에서 수명 분포를 추정하기 위해 ~ 3 nm 대역 통과를 갖는 모노크로메이터를 사용하여 고정 파장 세트에 대해 감쇠를 측정했습니다(그림 5). 낮은 강도로 인해 광자 계수 PMT 시스템이 이러한 목적으로 사용되었습니다. 효과적인 단색 복사를 사용하면 좁은 파장 범위에서 응답 함수의 분포가 무시할 수 있기 때문에 다른 검출기로 측정된 감쇠 상수에 차이가 없어야 합니다. 다른 실리콘 NC [25, 35, 36]에서 관찰된 것과 동일한 경향이 도데실 말단 입자에 대해 발견되었습니다. 즉, 분산 매개변수는 1에 가까울수록 증가하고 수명은 파장의 함수로 빠르게 증가합니다(그림 5, 표 3).
<그림>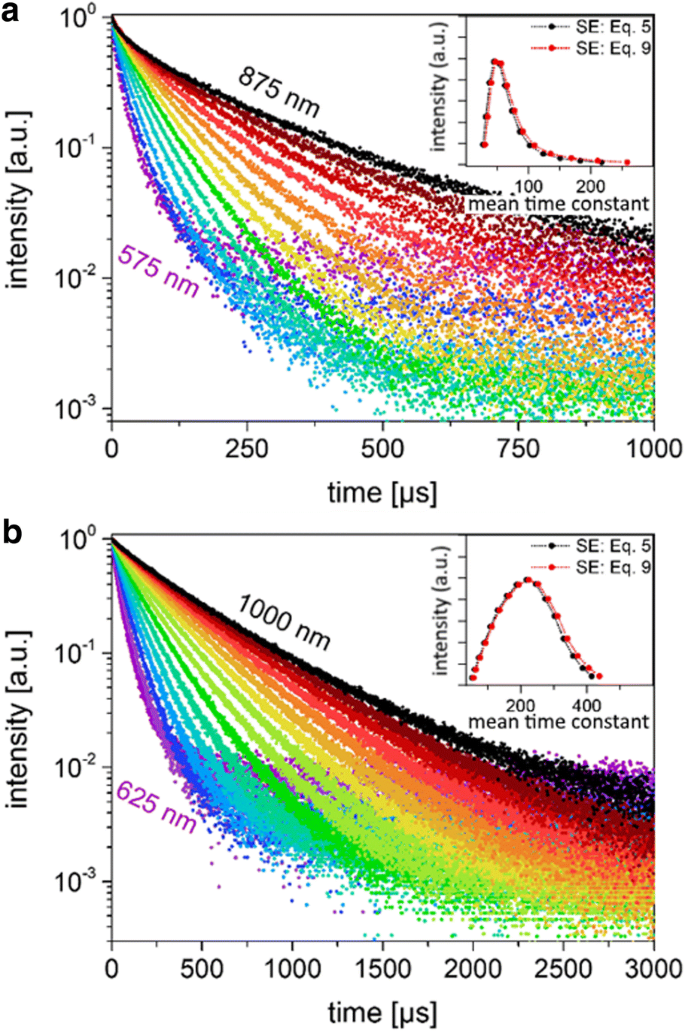
좁은 파장의 PL은 감쇠합니다. 아 발광은 25nm 간격으로 575~875nm 범위의 특정 방출 파장(3nm FWHM)에서 작은 SiNC에 대해 감쇠합니다. 데이터는 Eqs에 적합했습니다. 5와 9는 거의 단일 지수 피팅을 산출했습니다. ㄴ 동일한 조건에서 측정 및 장착된 큰 SiNC에 대해 625~1000nm 범위의 특정 방출 파장에서 발광이 감소합니다. 소형 및 대형 SiNC에 대한 결과 시간 상수는 표 1에 나와 있습니다.
더 작은 입자는 동일한 측정 파장에서 더 큰 입자보다 항상 더 짧은 수명을 가졌습니다. 이 관찰은 더 작은 입자의 더 낮은 AQY와 일치하며, 이는 큰 NC의 수명이 비복사 과정에 의해 덜 강하게 지배됨을 나타냅니다. 큰 NC는 또한 작은 NC 샘플에 비해 덜 산화됩니다(추가 파일 1 그림 S1). 따라서 작은 샘플에서 더 낮은 AQY의 관찰은 측정된 더 짧은 수명과 일치하지만 파장 선택을 통해 두 샘플을 상대적으로 비교할 수는 없습니다(기본적으로 방출 파장은 크기 및 산화 정도[24], 두 샘플에서 다름).
또한 그림 5에 삽입된 것으로 표시되는 것은 Eqs를 사용하여 단색 데이터에서 얻은 평균 수명을 표시하여 얻은 분포입니다. 해당 파장에서 PL 강도의 함수로 데이터에 맞게 5 또는 9를 선택합니다. 이러한 붕괴의 경우 베타 매개변수가 1에 상당히 가깝기 때문에 두 가지 버전의 SE 모델로 계산된 평균 수명과 이러한 방식으로 얻은 분포 사이에는 거의 차이가 없습니다. 이러한 붕괴는 I PL , 그럼에도 불구하고 수명 분포를 나타낼 수 있습니다. 작은 입자의 경우 ~ 47μs에서 피크를 관찰한 반면, 큰 NC의 경우 피크는 더 대칭적이며 220μs를 중심으로 합니다.
우리는 두 가지 테스트 표준에서 FRS 데이터를 검증하는 것으로 시작했습니다. 첫 번째는 RC 회로이고 두 번째는 형광성 Eu-킬레이트 도핑된 미소구체(Fisher Scientific)의 샘플입니다. RC 회로는 FRS 데이터가 Eq와 일치하는 단일 지수 감쇠를 가지고 있습니다. 9는 78.9μs의 측정된 감쇠 시간 상수와 일치하여 12.7kHz에서 매우 밀접하게 정점을 찍었습니다. Eu-킬레이트 PL 스펙트럼은 수백 마이크로초 정도의 감쇠 시간으로 650nm에서 정점을 이루며 Si NC에 대한 표준을 제시합니다. 발광도 670μs의 수명으로 거의 단일 지수적으로 감쇠했습니다. FRS 데이터는 ~ 1570Hz에 중심을 두었고 너비는 거의 같은 응답 함수(식 18)로 관찰된 TRS 결과에 상당히 가깝습니다. 차이(636 vs. 670 μs)는 아래에서 자세히 설명하는 것처럼 여기 방법과 결합된 감쇠의 약간 비지수적 동작 때문일 수 있습니다.
Si-NC에 대한 FRS 데이터는 관찰된 QFRS 결과가 응답 함수보다 약간 더 넓은 것으로 판명되었기 때문에 문제가 됩니다(그림 6a의 삽입 참조). 따라서 deconvolution 절차에서 심각한 문제를 피하기 위해 노이즈가 거의 없어야 하는 데이터에 대해 deconvolution을 수행해야 합니다. 우리는 포지티브 제약을 적용하기 위해 Richardson-Lucy 디콘볼루션 방법[37]을 사용했습니다. 그런 다음 분해되고 정규화된 QFRS 데이터는 사전에 어떤 모델도 가정하지 않고 각각 큰 NC와 작은 NC(빨간색 점)에 대해 그림 6에 표시된 대로 측정된 수명 분포를 직접 산출합니다. 두 샘플 모두에 대해 큰 NC의 경우 더 높은 주파수로 약간 치우친 반면 작은 NC 분포는 세미로그 플롯에서 더 거의 대칭적인 광범위한 수명 분포를 찾습니다. 감쇠율 분포는 작은 NC의 경우 19,900Hz(50.3μs)에서 정점을 찍은 반면, 큰 NC의 경우 분포는 6280Hz(159.2μs)에서 정점을 찍었습니다.
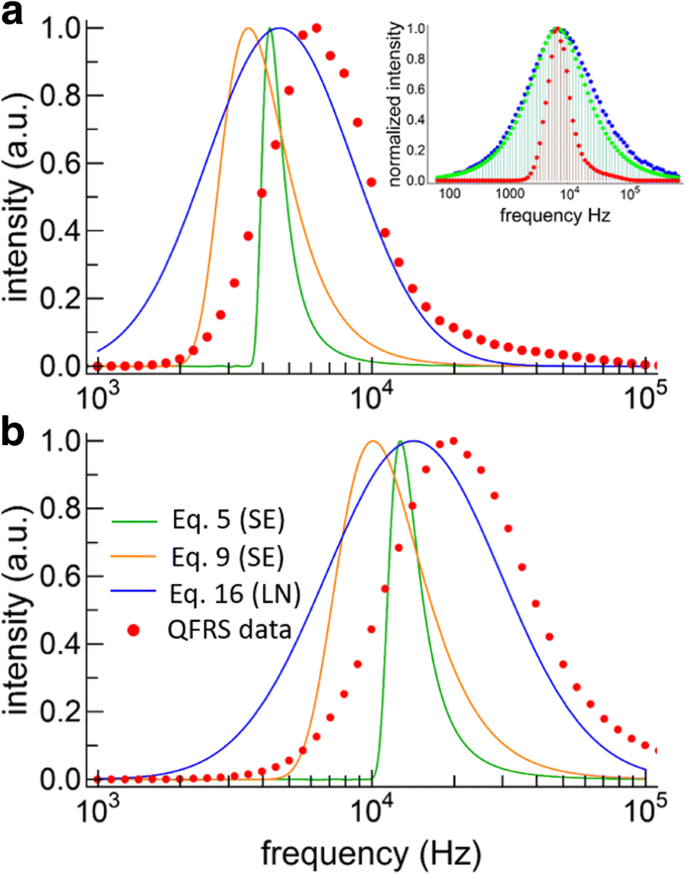
Lifetime distributions. 아 Lifetime distributions for large SiNCs obtained from fitting the TRS data with the two SE models and the LN model. The deconvolved QFRS data is also shown (red points). The inset shows the raw QFRS data for this sample (blue), the response function (green), and the deconvolution (red). ㄴ Lifetime distributions obtained by model fitting the TRS data (lines, same color scheme for both graphs) and QFRS (red points) for the small SiNCs
The lifetime distributions obtained from the stretched exponentials (orange and green curves) and lognormal (blue curve) model fits are also plotted in Fig. 6 for the large and small particles. The three decay models yield different distributions, both in terms of the overall shape and the peak frequencies. For both samples, the QFRS peaks at a higher frequency than any of the TRS model fits. While this may seem surprising, the same effects have been observed for CdSe NCs having a distribution of lifetimes [38, 39]. In fact, the TRS decay curve for CdSe NCs was evidently sensitive to the pulse duration, with shorter pulses accentuating the shorter lifetimes and the opposite case for long pulses. Furthermore, the mean lifetimes obtained by long-pulse duration techniques were a factor of 3–4 times longer than those obtained by phase measurement, which was due to preferential excitation of the long-lived population in steady-state excitation [38]. Indeed, the response function for TRS with a slow repetition rate is narrower than for FRS, cutting off especially sharply on the high frequency side [29]. Essentially, FRS accentuates the short-lived components of the ensemble decay more than steady-state TRS does, and this may account for the difference in the peak frequencies obtained by TRS model fitting and FRS. Despite these inherent differences, FRS appears suited to uncovering the distribution of lifetimes in ensembles of SiNCs, because it is obtained by direct measurement rather than by an assumed model. For SiNCs typical of a thermally grown ensemble, the main drawback of FRS is the necessity of a deconvolution.
While the detector response function certainly affects the QFRS, it plays a role in the TRS data as well. Indeed, measuring the ensemble decay with the APD vs. the PMT setup yielded mean decay times that were different by a factor of ~ 2, regardless of the fitting model applied. The detector responsivity also affects choice of the TRS “best” model fit. As mentioned above, our Thorlabs APD responsivity peaks at 600 nm, whereas for our Hamamatsu PMT the responsivity maximizes at 850 nm, in the long-wavelength, slow-decay part of the SiNC spectrum. Although apparently not reported before in the literature on SiNCs, this issue means that wide-spectrum TRS results from different setups are not comparable. Unfortunately, despite some critical conclusions, ref. [38] also used different detectors to compare the decay dynamics from the same wide-band NC sample and the response functions may not have been the same. Fortunately, however, the phase measurements and the steady-state measurements used the same detector (as was the case here) and the differences in the observed dynamics for these situations remain valid. Finally, the detector response function is in principle correctable in the FRS data if the responsivity curve and monochromated decay rate distribution are known over a wide range of wavelengths (i.e., decay rates). The responsivity correction has no such simple solution with TRS alone.
The most common models used for SiNC luminescence decay were described theoretically. The population decay corresponding to the “simple” stretched exponential luminescence decay, exp[− (t /τ ) β ], was derived and expressions for the characteristic mean times were found. This model was compared against the alternative model in which the population decays according to the simple SE. Two dodecene-functionalized SiNCs samples were then prepared from thermal nucleation and growth, followed by etching and alkane surface functionalization. These samples consisted of particles with mean diameters of 2.9 and 5.4 nm, respectively. The basic PL spectrum and TRS was measured using standard methods. The TRS data were fit with several distributions in order to establish whether any of them can be considered “true” and to find which one yields the best fit. While the simple SE luminescence decay fits the TRS data reasonably well, the distribution of residuals shows that it is not strictly accurate. None of the fitting models fully captures the shape of the measured decay rate distribution; they also show large deviations in the peak position and the shape of the distribution, as well as disagreement in the average time constants. Furthermore, the ensemble mean time constants were dependent on the responsivity curve of the detection system. This leads to serious questions about how to interpret the PL decay from ensembles of thermally-grown SiNCs.
Quadrature frequency-resolved spectroscopy was then employed with the intent to find the lifetime distribution directly for SiNC ensembles formed by thermal annealing of a base oxide. The spectrum was found to be not much wider than the intrinsic QFRS response function, requiring a deconvolution in order to extract the SiNC rate distribution. This yielded a distribution whose shape was nearly symmetrical (on a semilog scale) for the small NC sample and about half a decade wide, whereas it was slightly more skewed for the large NCs. We find that FRS techniques are suited to the study of SiNC luminescence dynamics and, after deconvolving the system response from the data, FRS yields the decay rate distribution directly. The most significant problem is the required deconvolution, but the Richardson-Lucy method was found to produce fairly robust results. While the detector response function can in principle be corrected from the FRS data, there is no simple means to do this for wide-PL-band TRS data. Still, as long as the data compared are from the same detector then the results should at least be internally meaningful. Hopefully in the future, these issues will be more fully considered when analyzing inhomogeneously broadened NC luminescence lifetimes, rather than defaulting to the simple stretched exponential model (Eq. 9) to describe and characterize the dynamical processes at work in the PL spectrum.
The SiNCs were synthesized according to a recently-proposed method [21]. Briefly, 4 g of hydrogen silsesquioxane (HSQ) was annealed at 1100 or 1200 °C for 1 h in a flowing 5% H2 + 95% Ar atmosphere, resulting in composites of SiNCs embedded in a silica matrix. These composites were mechanically ground into a fine powder using an agate mortar. The powder was shaken for about 8 h with glass beads using a wrist action shaker. The powders were suspended in 95% ethanol and interfaced to a vacuum filtration system equipped with a filter. To liberate the H-SiNCs, the silica matrix was removed via HF etching. An approximately 200 mg aliquot of the composite was transferred to a Teflon beaker to which 2 mL of ethanol, 2 mL of water, and 2 mL of 49% HF aqueous solution were added in order to dissolve the silica matrix. After stirring the suspension for 40 min, the liberated H-SiNCs were extracted as a cloudy yellow suspension using toluene and isolated by centrifugation at 3000 rpm for 5 min. The resulting hydrogen-terminated SiNCs were suspended in 10 mL dry toluene, and then transferred to an oven-dried Schlenk flask equipped with a magnetic stir bar. Subsequently, 1 mL of 1-dodecene (ca. 4.6 mmol), as well as 20 mg of AIBN were added. The suspension was subjected to three freeze-pump-thaw cycles using an Ar charged Schlenk line. After warming the suspension to room temperature, it was stirred for 24 h at 70 °C, and 10 mL of methanol and 20 mL of ethanol were subsequently added to the transparent reaction mixture. The resulting cloudy suspension was transferred to a 50 mL PTFE vial and the SiNCs were isolated by centrifugation at 12,000 rpm for 20 min. The SiNCs were re-dispersed in 10 mL toluene and isolated by addition of 30 mL ethanol antisolvent followed by another centrifugation. The latter procedure was carried out one more time. Finally, the dodecyl-SiNCs were re-dispersed in 5 mL dry toluene and stored in a screw capped vial (concentration ~ 0.5 mg/mL) for optical studies.
TEM samples were prepared by depositing the freestanding nanoparticles directly onto an ultrathin (ca. 3 nm) carbon-coated copper TEM grid. The NCs were imaged by bright-field TEM using a JEOL JEM-2010 and HRTEM was done on a JEOL JEM-ARM200CF. Fourier transform infrared spectroscopy (FTIR) was performed in a Nicolet 8700 from Thermo Scientific. X-ray photo-electron spectroscopy was measured in a SPECS system equipped with a Phoibos 150 2D CCD hemispherical analyzer and a Focus 500 monochromator. The detector angle was set perpendicular to the surface and the X-ray source was the Mg Kα line.
Luminescence spectra were excited with a 352-nm Ar + ion laser, which was pulsed (50% duty cycle, 50–250 Hz) using an Isomet IMDD-T110 L-1.5 acousto-optic modulator (AOM) with a fall time of ~ 50 ns. The used setup is schematically depicted in Fig. 7. The laser beam passes the acousto-optic modulator and one of the diffracted beams is selected by an iris. A beamsplitter reflects the main part of the pulsed laser beam into the sample cuvette and the incident power on the sample was ~ 8 mW spread over an area of ~ 4 mm 2 . The luminescence was collected with an optical fiber (numerical aperture 0.22), sent through a 450-nm longpass filter and is guided to the appropriate detector. The PL spectrum was measured by an Ocean Optics miniature spectrometer whose response function was corrected using a calibrated radiation source (the HL-3 + -CAL from Ocean Optics). The quantum efficiency was measured using an integrating sphere with 405-nm excitation, using a solution diluted to have an absorbance of ~ 0.15 at that wavelength.
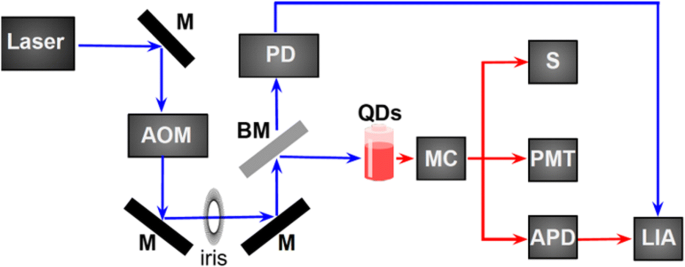
Diagram of the experimental setup. 엠 mirror, AOM acousto-optic modulator, BM beamsplitter, PD photodiode, MC monochromator, S spectrometer, PMT photomultiplier tube, APD avalanche photodiode, LIA lock-in amplifier
The luminescence dynamics were measured with two different detectors. The first detector was the Thorlabs 120A2 avalanche photodiode (50 MHz roll-off), which was interfaced to a Moku:Lab (200 MHz) in digital oscilloscope mode. The second detector was a Hamamatsu h7422-50 photomultiplier tube interfaced to a Becker-Hickl PMS400 multiscalar. The error in the luminescence decay times was obtained by repeating the measurements three times, yielding a standard error in the mean lifetime calculated using the stretched exponential fit (Eq. 4) of 1 μs. All fits to the decay data were done in Origin using the least linear squares with the Levenberg-Marquardt algorithm, and were repeated in Matlab using the same method. For wavelength-dependent decay measurements, the luminescence was sent through an Acton MS2500i monochromator prior to detection, with the half width of the detected radiation set to ~ 3 nm.
For QFRS measurements, the AOM was set to produce a sinusoidal oscillation. A part of the incident beam was deflected into a Thorlabs PDA10A photodiode (200 MHz) in order to generate the reference signal. The SiNC PL response was simultaneously collected and sent to the APD. The reference signal was obtained using the beamsplitter, and along with the corresponding PL signal, was analyzed using the Moku:Lab in the lock-in amplifier mode to measure the in-phase and quadrature components of the signal.
Finally, we also searched for a short-lifetime component in the luminescence, as has sometimes been reported previously and attributed to oxidation [22]. This system used a 405-nm picosecond diode laser (Alphalas GmbH) to excite the NCs, and a Becker-Hickl HPM-100-50 PMT interfaced to an SPC-130 pulse counter system. This setup has a response time of ~ 100 ps. No evidence of a nanosecond decay was observed in these SiNCs.
Avalanche photodiode
Absolute quantum yield
Frequency-resolved spectroscopy
Lognormal
Nanocrystals
광발광
Photomultiplier tube
Quadrature frequency-resolved spectroscopy
Stretched exponential
Silicon nanocrystals
Time-resolved spectroscopy
나노물질
초록 이 논문에서는 열 및 진동 보조제가 결합된 하이브리드 가공 공정 중 절단 메커니즘을 조사하기 위해 분자 역학 시뮬레이션을 수행합니다. 하나의 진동 주기에서 재료 제거 거동과 표면 아래 손상 형성을 연구하기 위해 수정된 절단 모델이 적용되었습니다. 결과는 하이브리드 가공 공정 동안 지배적인 재료 제거 메커니즘이 단일 진동 주기에서 압출에서 전단으로 변환될 수 있음을 나타냅니다. 절단 온도가 증가함에 따라 크랙의 발생 및 전파가 효과적으로 억제되고 지배적인 재료 제거 메커니즘이 전단될 때 팽창이 나타납니다. 하나의 진동 주기에서
전력 회사는 현대 장비 및 인프라에 대한 투자 필요성과 고객 비용 최소화 요구 사이의 균형을 유지하는 데 어려움을 자주 겪습니다. 상당한 요율 인상을 피하는 가장 효과적인 방법 중 하나는 모든 기존 자산의 평생 가치를 극대화하는 것입니다. 유틸리티는 자산 관리의 모범 사례를 활용하여 사용 수명을 개선하고 가장 가치 있는 투자에 대한 성능을 최적화합니다. ISO 55000과 같은 일부 확립된 규제 표준은 조직이 효과적인 자산 관리 시스템을 구축하고 유지하는 데 유용한 지침을 제공합니다. 유틸리티 산업(수도, 전기 등)의 다양한 측면과