나노물질








AlN의 굴절률은 발광 소자의 외부 양자 효율과 같은 AlGaN 기반 심자외선 광전자 소자에 직접적인 영향을 미칩니다. 고밀도 스레딩 전위가 일반적으로 AlN에 존재하기 때문에 스레딩 전위에 대한 AlN의 굴절률 의존성을 밝히는 것은 의미가 있습니다. 이 논문에서는 다양한 전위 밀도가 AlN의 굴절률에 미치는 영향을 조사했습니다. 4.24 × 10 8 에서 전위 밀도 증가 ~ 3.48 × 10 9 cm − 2 , AlN의 굴절률은 280 nm에서 2.2508에서 2.2102로 감소합니다. 추가 연구는 전위 주변의 나노 스케일 변형 장이 빛의 전파를 변화시켜 AlN의 굴절률을 감소시킨다는 것을 보여줍니다. 본 연구는 광전자소자의 설계를 통해 고성능의 심자외선 광전자소자를 구현하는데 도움이 될 것이다.
AlN 기반 재료는 발광 다이오드(LED)[1,2,3,4,5], 레이저 다이오드[6,7,8], 광검출기[6,7,8]와 같은 심자외선(DUV) 광전자 장치를 제조하는 유망한 재료입니다. 9, 10] 3.4에서 6.2eV로 조정할 수 있는 직접 밴드갭으로 인해 [11]. AlN의 굴절률은 광전자 소자의 성능에 직접적인 영향을 미칩니다. LED의 경우, 내부 전반사각이 AlN 층과 다른 영역 사이의 굴절률 차이에 의해 결정되기 때문에 AlN의 굴절률은 광추출 효율(LEE)에 영향을 미치며, 이는 양에 대한 주요 제한 요소입니다. 광 출력의. 외부 양자 효율(EQE)은 내부 양자 효율과 LEE의 곱이므로 AlN의 굴절률은 LED의 EQE에 영향을 미칩니다. 또한 굴절률은 반사율이 굴절률에 민감한 DBR(Distributed Bragg Reflector)[12,13,14]과 같은 도파관 구조의 설계에서 중요한 역할을 합니다. 따라서 AlN의 굴절률에 영향을 미치는 요인을 밝히는 것이 중요합니다. AlN의 굴절률은 온도, 압력 및 밴드갭을 비롯한 많은 요인에 의해 영향을 받을 수 있음을 선행 연구에서 알 수 있습니다. AlN의 굴절률은 온도가 높을수록[15] 압력이 낮을수록 증가합니다[16]. AlN 기반 재료의 경우 밴드갭이 증가함에 따라 굴절률이 낮아집니다[17]. 또한 반도체의 전위는 반도체의 특성과 소자의 성능에 큰 영향을 미친다. 전위는 재료의 응력을 해제합니다[18]. 그것들은 또한 광검출기의 암전류와 반응성에 영향을 미치고[19] 다중 양자 우물의 IQE에 영향을 미칠 것입니다[11, 20]. 그러나 AlN 재료에 높은 TDD가 있으며 일반적으로 10 8 에서 다양하지만 다양한 나사 전위 밀도(TDD)가 AlN의 굴절률에 미치는 영향에 초점을 맞춘 연구는 거의 없습니다. ~ 10 9 cm − 2 최근 보고서의 주문 [21,22,23]. TDD와 AlN의 굴절률 사이의 상관 관계를 조사하는 것은 광전자 장치의 성능을 최적화하는 열쇠입니다. 이 논문에서는 AlN의 굴절률에 대한 다양한 TDD의 의존성을 연구했습니다. 633 nm, 365 nm 및 280 nm와 같은 다른 광자 파장이 사용됩니다. 결과는 전위가 AlN의 굴절률 감소로 이어진다는 것을 보여줍니다. 결과는 DUV LED 및 DBR 구조와 같은 AlN 기반 광전자 장치의 설계 및 시뮬레이션에 도움이 될 것입니다.
전위와 AlN의 굴절률 사이의 관계를 연구하기 위해 c-사파이어 기판에서 금속 유기 화학 기상 증착(MOCVD)에 의해 AlN 템플릿을 성장시킨 다음 다른 온도에서 어닐링하여 전위 밀도가 다른 AlN 샘플을 얻었습니다.
MOCVD에 의해 AlN 템플릿을 성장시킬 때, 트리메틸알루미늄과 암모니아가 전구체 가스로 사용되었습니다. 수소는 캐리어 가스로 사용되었습니다. 성장 중 압력은 40 mbar로 유지되었습니다. 핵형성층의 성장 온도와 시간은 150 s 동안 약 955 °C이고 고온(HT) AlN 성장을 위해 1280 °C까지 상승합니다. 15분간의 고온 AlN 성장 후, AlN 중간층은 1050°C에서 160초 동안 성장되었다. 마지막으로, 성장 온도를 1280°C까지 올려 두꺼운 HT AlN을 50분 동안 성장시켰다. AlN 필름의 총 두께는 약 1.1 μm입니다.
MOCVD에 의한 AlN 층의 성장 후, AlN 템플릿은 1 시간 동안 각각 1500 °C, 1600 °C, 1700 °C 및 1750 °C에서 ex situ 열처리되었습니다. 열처리하지 않은 AlN층을 샘플 1로, 1500 °C~1750 °C 열처리 후의 샘플을 샘플 2~5로 표시하였다. X선 회절(XRD)을 이용하여 AlN 샘플의 TDD를 측정하였으며, 분광 타원 측정(SE) 측정을 통해 굴절률을 측정했습니다. AlN 템플릿의 응력 상태를 특성화하기 위해 라만 이동 스펙트럼이 채택되었습니다.
그림 1a 및 b는 5개의 AlN 샘플의 (0002) 및 (10-12) 평면 XRD 요동 곡선(XRC)을 보여줍니다. (0002) 평면 XRC의 반치폭(FWHM)이 약간 감소하고 (10–12) 평면 XRC의 FWHM이 샘플 1에서 샘플 5로 크게 감소하는 것을 관찰할 수 있습니다. 나사 및 모서리 전위의 밀도 구성 요소는 공식 (1) 및 (2)에 따라 (0002) 및 (10–12) 평면 XRC의 FWHM을 사용하여 계산할 수 있습니다. [24, 25].
$$ {\rho}_{\mathrm{s}}={\beta_{(0002)}}^2/\left(2\pi \ln 2\times {\left|{b}_c\right|} ^2\right) $$ (1) $$ {\rho}_{\mathrm{e}}={\beta_{\left(10-12\right)}}^2/\left(2\pi \ ln 2\times {\left|{b}_a\right|}^2\right) $$ (2)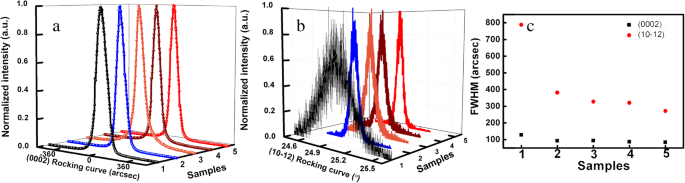
아 5개의 AlN 샘플의 (0002) 평면 XRC. ㄴ 5개의 AlN 샘플의 (10-12) 평면 XRC. ㄷ (0002, 10-12) 평면 XRC의 FWHM; 빨간색 원은 (10-12) 평면의 FWHM을 의미하고 검은색 사각형은 (0002) 평면의 FWHM을 나타냅니다.
여기서 ρ s 및 ρ e 나사 및 모서리 성분으로 전위의 밀도를 각각 나타냅니다. β XRC의 FWHM입니다. |ㄴ ㄷ | c축 격자 상수와 동일하고 |b 아 | AlN의 a축 격자 상수와 동일합니다. (0002) 및 (10-12) 평면 XRC의 FWHM은 5개의 AlN 샘플에 대한 그림 1c에 표시되고 5개의 AlN 샘플의 계산된 TDD는 표 1에 표시됩니다.
5개 샘플의 SE 실험 데이터는 직접 밴드 갭 반도체의 광학적 특성을 효과적으로 재현할 수 있는 파라메트릭 반도체 모델을 사용하는 CompleteEASE 소프트웨어(J.A. Woollam Inc.)에 의해 피팅되었습니다[26]. 그림 2a는 5개 샘플의 부분 실험 및 피팅 곡선을 보여줍니다. 5개 표본의 평균 제곱 오차(MSE)는 각각 8.139, 8.536, 9.175, 10.560, 9.821로, 이는 좋은 적합 결과를 확인시켜줍니다. 모든 데이터 및 피팅 결과는 추가 파일 1에 제공됩니다.
<사진>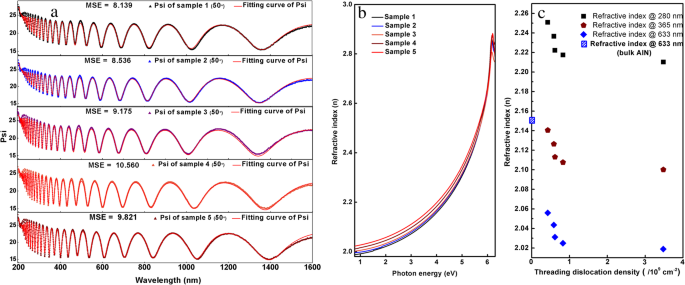
아 SE 측정 및 피팅 곡선의 부분 실험 데이터. ㄴ 굴절률 곡선. ㄷ 280 nm, 365 nm 및 633 nm에서 굴절률과 다른 TDD 비교
5개 샘플의 굴절률 곡선은 그림 2b와 같이 피팅 결과에서 얻을 수 있습니다. 광자 에너지가 AlN의 밴드갭(약 6.2 eV)보다 낮을 때 굴절률은 5개 샘플 모두의 광자 에너지가 증가함에 따라 증가합니다. 그러나 광자 에너지가 6.2 eV보다 높으면 광자 에너지가 증가함에 따라 굴절률이 감소합니다. 이 현상은 Kramers-Krőnig 분산 관계로 설명할 수 있습니다. AlN의 TDD가 감소함에 따라 굴절률은 633 nm에서 2.019에서 2.056으로 증가하며, 이는 벌크 AlN(633 nm에서 2.15)에 더 가깝습니다[27]. 이는 AlN의 전위가 벌크 AlN 결정의 굴절률보다 작은 굴절률을 만든다는 것을 의미합니다.
4.42 eV(280 nm, 태양광 차단 UV), 3.40 eV(365 nm, GaN 밴드갭) 및 1.96 eV(633 nm)에서 굴절률과 TDD 사이의 관계는 표 2c와 표 1에 나와 있습니다. TDD의 증가에 따라 AlN의 굴절률이 감소함을 알 수 있다. 4.24 × 10 8 에서 전위 밀도 증가 ~ 3.48 × 10 9 cm − 2 , AlN의 굴절률은 280 nm에서 2.2508에서 2.2102로 감소합니다.
전위가 AlN의 굴절률을 어떻게 변화시키는지에 대한 메커니즘을 밝히기 위해 전위에 의해 유도된 변형장이 연구됩니다. 굴절률과 스트레인 필드 사이의 관계는 식 (3)으로 설명됩니다[28]:
$$ \Delta {\left(\frac{1}{n^2}\right)}_i=PS=\sum \limits_{ij}{p}_{ij}{s}_j $$ (3)공식에서 p ij 탄성 광학 텐서 및 S 스트레인의 존재입니다. 광탄성 상수 행렬 P wurtzite AlN은 식 (4) [29, 30]과 같이 표시됩니다.
$$ p=\left(\begin{array}{l}-0.1\kern1.75em -0.027\kern0.75em -0.019\kern1em 0\kern3em 0\kern2.75em 0\\ {}-0.027\kern0.5em -0.1\kern2em -0.019\kern1em 0\kern3em 0\kern2.75em 0\\ {}-0.019\kern0.5em -0.019\kern1em -0.107\kern1em 0\kern3em 0\kern2.75em 0\\ kern2.75em 0\kern3em 0\kern3.5em -0.032\kern0.75em 0\kern2.75em 0\\ {}0\kern2.75em 0\kern3em 0\kern3.5em 0\kern3em -0.032\0kern0.5 \\ {}0\kern2.75em 0\kern3em 0\kern3.5em 0\kern3em 0\kern2.75em -0.037\end{배열}\right) $$ (4)AlN의 나사 전위 및 모서리 전위의 변형장 매트릭스가 고려됩니다. 두 종류의 전위에 대한 원통형 링 모델은 그림 3에 설명되어 있습니다. 모델에 따라 단일 전위 주변의 변형장의 분포를 얻을 수 있습니다[31, 32].
<그림>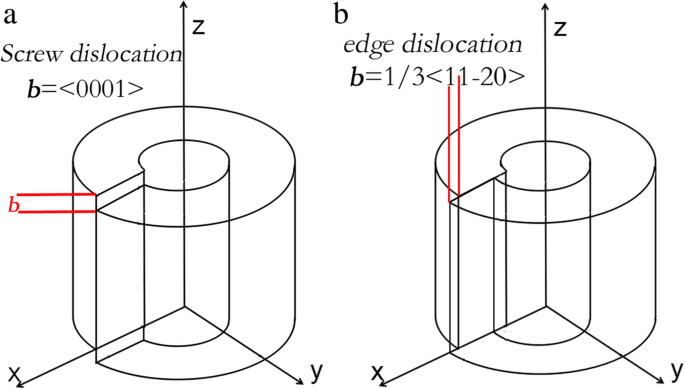
a의 원통형 링 모델 나사 탈구 및 b 가장자리 전위
단위 나사 전위 주변의 변형장은 다음과 같이 쓸 수 있습니다.
$$ {e}_{xz}={e}_{zx}=-\frac{b}{4\pi}\frac{y}{\left({x}^2+{y}^2\ 오른쪽)} $$ (5) $$ {e}_{yz}={e}_{zy}=\frac{b}{4\pi}\frac{x}{\left({x}^2 +{y}^2\right)} $$ (5a) $$ {e}_{xx}={e}_{yy}={e}_{zz}={e}_{xy}={ e}_{yx}=0 $$(5b)단위 가장자리 전위 주변의 변형장은 다음과 같이 쓸 수 있습니다.
$$ {e}_{xx}=-\frac{b}{4\pi \left(1-v\right)}\frac{y\left({x}^2-{y}^2\right )}{{\left({x}^2+{y}^2\right)}^2}-\frac{b}{2\pi}\frac{y}{\left({x}^2 +{y}^2\right)} $$ (6) $$ {e}_{yy}=\frac{b}{4\pi \left(1-v\right)}\frac{y\left (3{x}^2+{y}^2\right)}{{\left({x}^2+{y}^2\right)}^2}-\frac{b}{2\pi }\frac{y}{\left({x}^2+{y}^2\right)} $$ (6a) $$ {e}_{zz}=\frac{b\left(\lambda - 2 v\lambda -2 Gv\right)}{2\pi \left(2G+\lambda \right)\left(1-v\right)}\frac{y}{x^2+{y}^2} $$ (6b) $$ {e}_{xy}={e}_{yx}=\frac{b}{4\pi \left(1-v\right)}\frac{x\left({ x}^2-{y}^2\right)}{{\left({x}^2+{y}^2\right)}^2} $$ (6c) $$ {e}_{xz }={e}_{zx}={e}_{yz}={e}_{zy}=0 $$ (6d)여기서 b 단위 전위의 Burgers 벡터의 길이이며 e 전위 주변의 변형률을 나타냅니다. 지 =121 GPa는 wurtzite AlN의 전단 계수입니다. λ =117.1 GPa 및 v =0.241은 각각 절름발이 상수와 푸아송 비[33, 34]입니다. e 간의 통신에 따르면 이 그리고 S ㅋ (나 ,j =x ,y ,z; ㅋ =1,2,3...6) [35], 전위에 의한 굴절률의 변화를 더 나타내기 위해 아래와 같이 변형장을 매트릭스 형성으로 변환한다.
$$ {S}_{\mathrm{edge}}=\left({S}_1\kern0.5em {S}_2\kern0.5em {S}_3\kern0.5em 0\kern0.5em 0\kern0. 5em {S}_6\right) $$ (7) $$ {S}_{\mathrm{나사}}=\left(0\kern0.5em 0\kern0.5em 0\kern0.5em {S}_4\ {S}_5\kern0.5em 0\right) $$ (8)행렬 (7)과 (8)을 공식 (3)으로 가져오면 다음 식을 얻을 수 있습니다. Δn 단위 나사 및 단위 모서리 전위로 인해 발생합니다.
$$ \Delta {\left(\frac{1}{n^2}\right)}_{\mathrm{screw}}={\left(\frac{1}{n_1^2}-\frac{1 }{n_0^2}\right)}_{\mathrm{나사}}=-0.032\left({S}_4+{S}_5\right)=-0.008\frac{b\left(xy\right)} {\pi \left({x}^2+{y}^2\right)} $$ (9) $$ \Delta {\left(\frac{1}{n^2}\right)}_{ \mathrm{edge}}={\left(\frac{1}{n_1^2}-\frac{1}{n_0^2}\right)}_{\mathrm{edge}}=-0.146\left( {S}_1+{S}_2\right)-0.145{S}_3-0.037{S}_6=\hbox{-} 0.146\left(\frac{b}{4\pi \left(1-v\right) )}-\frac{b}{2\pi}\right)\frac{2y}{x^2+{y}^2}-0.145\frac{b\left(\lambda -2\lambda v-2 Gv\right)}{2\pi \left(2G+\lambda \right)\left(1-v\right)}\frac{y}{x^2+{y}^2}-0.037\frac{b }{4\pi \left(1-v\right)}\frac{x\left({x}^2-{y}^2\right)}{{\left({x}^2+{y }^2\오른쪽)}^2} $$ (10)계산에 기초하여 단위 나사 및 단위 모서리 전위 주변의 굴절률 분포(예:633 nm)는 그림 4에 나와 있습니다. 전위 주변의 굴절률은 반경 방향을 따라 변하는 것을 나타냅니다. 불균일한 매체로 간주될 수 있는 전위 코어에서. 따라서 AlN에서 전파되는 빛은 상응하게 TDD의 영향을 받습니다. 빛이 전위 주변의 이러한 굴절 필드를 통과할 때 산란과 간섭이 발생합니다[36]. 결과적으로 AlN의 굴절률이 변경되며 이는 비균질 매질의 산란 매트릭스에 해당합니다[37].
<그림>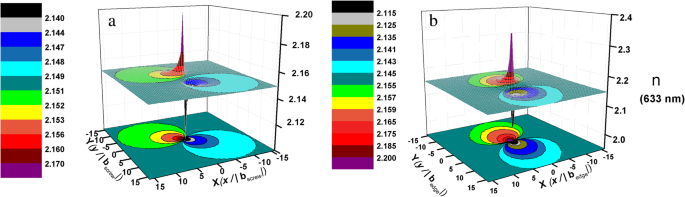
a 주변의 633 nm에서 굴절률 분포 단위 나사 전위 및 b 단위 가장자리 전위
"소개" 섹션에서 언급했듯이 굴절률이 전위에 의해 실제로 영향을 받는다는 것을 증명하려면 다른 영향 요인을 제거해야 합니다. 모든 샘플은 온도의 영향을 피하기 위해 실온에서 측정되었습니다. AlN 재료에서 응력의 영향을 피하기 위해 Raman 스펙트럼을 사용하여 AlN 응력을 확인하고 그 결과를 그림 5에 나타내었습니다. E g 750 cm − 1 에서 사파이어의 모드 피크 교정으로 간주됩니다. AlN E의 라만 이동 피크 2 (h ) 표 1과 같이 TDD의 감소에 따른 청색 이동. E의 청색 이동 2 (h ) 피크는 AlN이 사파이어 기판으로부터 점점 더 많은 압축 응력을 받는다는 것을 의미합니다. 그러나 압축 응력이 증가함에 따라 굴절률은 633 nm에서 벌크 AlN의 굴절률에 가까워집니다. AlN의 응력이 불균일 기판에서 받는 응력은 굴절률에 거의 영향을 미치지 않음을 분명히 알 수 있습니다. 결론을 뒷받침하는 추가 증거는 AlN이 Si 기판으로부터 인장 응력을 받을 때 AlN의 굴절률이 벌크 AlN의 굴절률보다 작다는 것입니다[38]. 이는 이 연구에서 AlN이 압축 응력을 받는 조건과 동일합니다. 이 현상은 AlN의 굴절률에 큰 변화를 주기에는 기판이 받는 응력이 너무 작기 때문일 수 있습니다. 결과적으로 다른 요인의 영향과 비교하여 AlN의 굴절률에 대한 기판의 응력 영향은 무시할 수 있습니다.
<그림>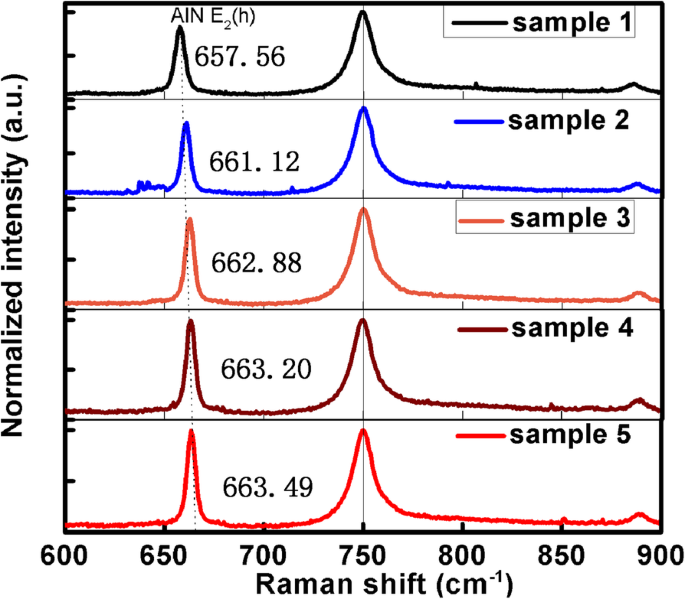
5개 샘플의 라만 이동 스펙트럼
5개 샘플의 밴드갭도 여기에서 계산됩니다. 광흡수 계수 α SE 피팅 결과에서 추출한 다음 밴드갭 E g 아래 공식에 따라 계산됩니다[39]:
$$ {\left(\alpha E\right)}^2=\left\{\begin{array}{c}C\left(E-{E}_g\right)\kern0.75em \left(E\ ge {E}_g\right)\\ {}0\kern4.75em \left(E<{E}_g\right)\end{array}\right. $$ (11)(αE의 플롯 ) 2 대 E x의 절편은 그림 6과 같습니다. -축은 E의 값입니다. g . x의 피팅 곡선의 절편에서 -축, 샘플 1에서 샘플 5에 대해 6.1106에서 6.1536 eV로 증가하는 밴드갭이 그림 6에 나와 있습니다. 굴절률과 밴드갭 사이의 관계는 다음과 같습니다[16].
$$ n(E)={\left[a{\left(\frac{E}{E_g}\right)}^2\left(2-{\left(1+\frac{E}{E_g}\ right)}^{0.5}-{\left(1-\frac{E}{E_g}\right)}^{0.5}\right)+b\right]}^{0.5} $$ (12) <그림>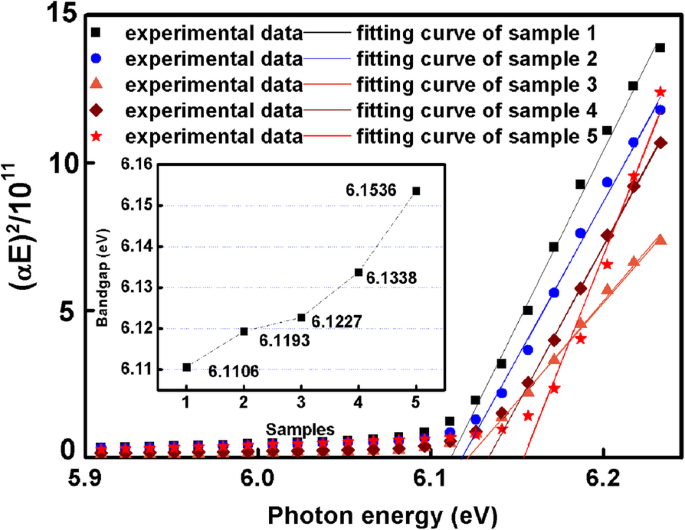
(αE의 의존성 ) 2 에 (E ), 삽입 그림은 AlN 템플릿의 밴드갭을 보여줍니다.
여기서 E 는 광자 에너지이고 E g 는 AlN의 밴드갭입니다. 아 그리고 b AlN에 대해 각각 13.70 및 7.81에 해당하는 상수입니다. AlN의 굴절률은 E가 증가함에 따라 감소해야 합니다. g 공식에 따르면. 그러나 본 연구에서는 E의 증가에 따라 AlN의 굴절률이 증가한다. g 이는 TDD의 영향에 비해 AlN의 굴절률에 대한 밴드갭의 영향을 무시할 수 있음을 의미합니다. 따라서 TDD의 변화는 AlN의 굴절률 변화에 중요한 역할을 한다.
위의 분석과 결합하여 나노 스케일 스트레인 필드가 전위 주변의 굴절률 분포에 영향을 미치고 AlN의 굴절률에 추가로 영향을 미치는 것으로 확인되었습니다. 전위는 실험 데이터에 따라 AlN의 굴절을 감소시킵니다.
결론적으로, AlN의 굴절률에 대한 TDD의 효과는 실험적으로나 이론적으로 연구되었다. 온도, 응력 및 밴드갭의 영향을 배제하면 TDD가 증가함에 따라 AlN의 굴절률이 감소한다는 결론을 얻을 수 있습니다. 추가 연구에 따르면 전위 주변의 나노스케일 변형 장은 전위 주변에서 굴절률이 크게 변하는 것으로 나타났습니다. 빛이 전위를 통해 전파되면 산란과 간섭이 발생하여 AlN의 굴절률이 변경됩니다. 이 연구의 발견은 AlN 기반 DUV 광전자 장치를 최적화하는 데 도움이 될 것입니다.
모든 데이터는 적절한 요청에 따라 제공될 수 있습니다.
분산 브래그 반사경
심자외선
외부 양자 효율
최대 절반에서 전체 너비
발광 다이오드
광추출 효율
금속-유기 화학 기상 증착
평균 제곱 오차
분광 타원 측정
스레딩 전위 밀도
XRD 요동 곡선
X선 회절
나노물질
고객은 자주 방문하는 비즈니스에서 더 많은 것을 기대합니다. 실제로 비즈니스 리더의 70%는 팬데믹 이후 고객 요구가 강화되었다고 말합니다. 유틸리티 회사이든 고객의 비즈니스 또는 가정에서 서비스를 제공하든 관계없이 서비스를 제공하는 사람들을 돌보기 위해 적절한 현장 서비스 관리가 필요합니다. 하지만 이런 환경에서는 현장 봉사를 잘하기가 어렵습니다. 비즈니스가 성장하고 방정식에 더 많은 움직이는 부분을 추가함에 따라 특히 어렵습니다. 모든 현장 서비스 운영자는 어떤 종류의 프로세스와 이러한 프로세스가 작동하도록 하는 올바른
우리가 3D 프린팅이라고 부르는 것은 일반적으로 금형 제조, 산업 디자인 및 기타 분야에서 사용됩니다. 또한 식품 분야에서 3D 프린팅 기술도 중요한 발전을 이루었습니다. 3D 프린팅의 장점 1. 조작이 간단하고 편리합니다. 전통적인 선반의 제조 공정은 작업자가 오랜 시간 동안 작동 방법과 기술을 배워야 합니다. 그러나 3D 프린팅은 컴퓨터 소프트웨어의 작동과 기계의 캘리브레이션만 알면 되며 전체 작동 프로세스는 장기간의 연구 없이 마스터할 수 있습니다. 기존 선반 제조 공정에 비해 훨씬 간단합니다. 2. 생산 효율성 향상 3D