나노물질








우리는 이론적으로 Rashba 스핀-궤도 결합(RSOC)으로 인한 두 개의 평행선 결함이 있는 실리신의 계곡 분극을 조사합니다. RSOC가 고유 스핀-궤도 결합(SOC)을 초과하는 한 두 계곡의 전송 계수는 동일한 주기와 강도로 진동하며, 이는 넓은 전송 피크와 제로 전송 안정기로 구성됩니다. 그러나 수직 전계가 존재하면 첫 번째 계곡의 진동 주기가 증가하는 반면 두 번째 계곡의 진동 주기는 짧아져 완벽한 계곡 분극이 달성될 수 있는 대응하는 넓은 피크-제로 고원 영역이 생성됩니다. 또한, 전기장의 세기를 조절하여 밸리 분극도를 1에서 -1로 변경할 수 있습니다. 우리의 발견은 순수한 전기 수단으로 밸리 분극 전류를 생성하는 다른 경로를 설정하고 반도체 밸리트로닉스의 흥미로운 응용 분야에 대한 문을 엽니다.
실리콘 원자의 버클이 낮은 단층 벌집 격자인 실리콘은 밸리트로닉 응용 분야에서 그래핀에 대한 잠재적으로 매력적인 대안입니다. 낮은 버클 구조는 실리신에서 상대적으로 큰 SOC(spin-orbit coupling)를 발생시키며 Dirac 지점 K에서 약 1.55meV의 상당한 에너지 갭이 추정됩니다. 및 K ′ [1] 그래핀과 달리 실리센의 저에너지 분산 관계는 선형이 아닌 포물선 형태이다. 버클링 구조에 의해 촉진된 실리신의 밴드 구조는 전기장을 인가하여 제어할 수 있으며, 양자 스핀 홀 절연체에서 양자 밸리 홀 절연체로 위상 전이(topological phase transition)도 일어날 수 있다[2, 3]. 규소는 Ag(111), Ir(111), ZrB2(0001)[4-6]와 같은 기판 표면에서 성공적으로 합성되었으며, 여러 이론 연구에서 자립형 안정 구조가 예측되었습니다. ]. 가장 중요한 것은 실온 실리신 전계 효과 트랜지스터(FET)가 실험적으로 성공적으로 관찰되었다는 것입니다[8]. 전기장 조정 가능성 및 기존 실리콘 기반 장치와의 호환성으로 인해 silicene은 차세대 Valleytronics에 적용할 수 있는 잠재적인 2차원 재료가 됩니다.
그래핀 및 전이금속 디칼코게나이드(MoS2 등), 서로 다른 결정학적 방향을 가진 물질의 두 영역 사이의 결정립 경계는 골 분극을 달성하기 위한 이상적인 선택이며 상당한 관심을 끌고 있습니다[9-14]. 최근 silicene의 ELD(Extended Line Defect)가 제1원리 계산에 따라 광범위하게 조사되었으며[15, 16], 5-5-8 ELD(이하 "선 결함"으로 약칭)는 다음과 같은 것으로 밝혀졌습니다. 가장 안정적이고 가장 쉽게 형성되는 구조 실리신 라인 결함의 스핀 및 밸리 분극이 이론적으로 조사되었다[17-19] 라인 결함의 형성은 흡착된 Si 원자, 여기서 선 결함의 양쪽은 유사 가장자리 상태와 유사한 거동을 나타내고 지그재그 가장자리의 결정립계는 유사 가장자리로 작용합니다[16] 분명히 이러한 격자는 선에 대해 거울 대칭을 갖습니다. 결함과 결함으로 분리된 "왼쪽" 및 "오른쪽" 영역의 해당 격자 벡터는 반대입니다[10, 11]. 반전 영역 경계가 있는 이러한 선 결함에서 A /나 부격자와 계곡 지수는 결함을 교차할 때 교환됩니다. 라인 결함은 그래핀의 준 입자에 대해 반투명하고 높은 입사각에서 높은 골 분극이 나타납니다. 계곡 편광은 q입니다. 와 (y를 따라 전자의 그룹 속도 방향) 라인 결함에 따라 다릅니다. 선형 분산과 일정한 그룹 속도를 갖는 그래핀의 경우 계곡 분극은 크게 |q에서 거의 100%에 도달할 수 있습니다. 와 | (높은 입사각에 해당) |q로 감소합니다. 와 | |q로 줄어들고 사라집니다. 와 |∼0 [9, 14]. 대조적으로, silicene은 두 가지 다른 투과 특성을 갖는다[17, 18]. 첫째, 페르미 에너지가 포물선 분산 관계로 인해 대역 가장자리에 가까우므로 두 골을 구별할 수 없게 되며, 둘째, 나선형으로 인해 투과가 제한됩니다. 그림 1c와 같이 라인 결함의 양쪽에 역으로 흐르는 에지 상태. 당연히 특정 RSOC에 SOC가 있는 시스템은 효율적인 스핀 FET의 유망한 후보입니다. RSOC는 평면 내 유효 자기장을 생성하고 구속 평면에 수직으로 주입되는 스핀 세차를 유도합니다. 스핀 분극[20]과 반전[21]은 게이트된 실리센 나노리본에서 조사되었습니다. 이론적 계산에 따르면 실리신의 에너지 밴드는 RSOC에 의해 크게 변조될 수 있습니다[22, 23]. 예를 들어, 상대적으로 강한 RSOC에서 K의 스핀다운(-업) 밴드 (케이 ′ ) 밸리는 위로 이동하는 반면 전도대의 다른 스핀 밴드는 변경되지 않습니다. 실리신 라인 결함의 고유한 전송 특성과 실리신에서 RSOC의 영향을 고려하여 밸리 편광 캐리어를 생성하기 위한 실용적인 완전 전기 방식이 가능합니다.
<그림>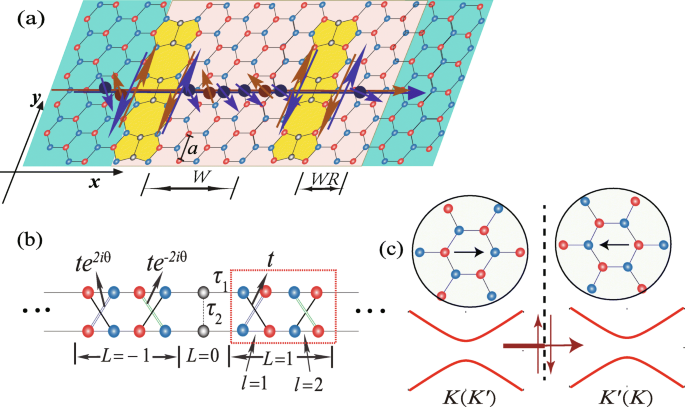
아 상태의 세차 과정의 개략도(K ,↑ )(빨간색 구) 및 (K ′ ,↓ )(파란색 구) 두 개의 평행선 결함이 있는 실리신 시트를 통과합니다. 여기서 파란색(빨간색) 원은 A를 나타냅니다. (B ) 부격자. 상태(K ,↑ ) 및 (K ′ ,↓ )은 pseudo-edge를 따라 순환하고 RSOC와 전기장은 프렌치 그레이 영역에 존재한다고 가정합니다. 와 (와 =2) 및 WR (WR =1) \(\sqrt {3}a\) 단위로 산란 영역의 너비를 나타냅니다. ㄴ 라인 결함이 있는 무한 실리신의 단순화된 격자 모델, 여기서 θ =카 와 아 점선 직사각형은 슈퍼셀에 해당합니다. 단위 셀에서 격자점은 일련의 인덱스(L,l ). ㄷ K의 한 스핀 상태에 대한 전송 (케이 ′ ) 반전 영역 경계가 있는 라인 결함을 가로지르는 계곡. 삽입된 부분은 선 결함(점선)으로 분리된 두 영역에서 결정 격자의 방향을 보여줍니다. 굵은 선/가는 선은 의사 에지를 따라 역으로 흐르는 나선형 에지 상태로 인해 선 결함을 가로질러 전송이 제한됨을 나타냅니다.
이 논문에서 우리는 silicene 이중선 결함을 사용하여 서로 다른 밸리의 Dirac 페르미온을 분극화하는 효율적인 방법을 제안하여 실리신의 전기장을 활용하여 뚜렷한 밸리 분극을 생성합니다. 우리의 결과는 페르미 에너지가 전도대의 바닥 근처에 있을 때 넓은 진동 피크와 최저점을 포함하는 두 계곡에서 전송 계수의 진동 이미지가 RSOC가 고유 SOC를 초과하는 한 일치한다는 것을 보여줍니다. 단일 라인 결함은 밸리 종속 전자를 분산시킬 수 없습니다. 두 개의 평행선 결함이 관련되면 진동하는 최하점이 제로 전송 고원으로 발전하고 수직 전기장으로 두 Dirac 계곡의 진동 주기를 변경하여 계곡 종속 전송의 효과적인 변조를 실현할 수 있습니다. 두 계곡은 증가 및 감소하고 넓은 피크-제로 고원 해당 영역에서 완벽한 계곡 분극으로 이어집니다. 실험에서는 전기장에 의한 컨덕턴스의 변화를 측정하여 이러한 순수한 밸리 전류를 감지할 수 있습니다. 이 현상은 RSOC 및 전기장을 활용하여 실리신 장치에서 밸리 분극을 효과적으로 변조하기 위한 다른 경로를 제공합니다.
RSOC 및 전기장으로 인해 밸리 분극 전류를 생성하기 위해 스핀 세차를 나타내는 그림 1a와 같이 2단자 실리신 라인 결함 장치의 개략도부터 시작하겠습니다. 폭이 W인 라인 결함의 한쪽에 RSOC가 존재한다고 가정합니다. 및 WR \(\sqrt {3}a\) 단위, 여기서 a =3.86 Å은 그림 1a와 같이 깨끗한 실리센의 격자 상수입니다. 페르미 에너지가 전도대의 맨 아래에 있을 때 상태(K ,↓ )[ (케이 ,↓ ) 계곡 K의 상태에 해당 ↓와 함께 (아래) 스핀] 및 (K ′ ,↑ ) RSOC의 에너지 밴드 조작으로 인해 격차에 있습니다. 다른 두 상태(K ,↑ ) 및 (K ′ ,↓ ), 그림 1a와 같이 SOC[24]의 스핀-모멘텀 잠금 특성으로 인해 의사 모서리를 따라 순환합니다. 확실한 스핀 상태의 경우 그림 1c에서와 같이 필터 역할을 하고 라인 결함을 가로지르는 전송을 억제할 수 있는 라인 결함의 양쪽에서 반대 방향으로 의사 가장자리를 따라 흐릅니다.
꽉 바인딩 표현의 격자 모델은 RSOC가 있는 라인 결함 시스템을 설명하는 데 사용됩니다. [17, 22]
$$\begin{array}{@{}rcl@{}} H&=&t\sum_{\langle i,j\rangle\alpha}c_{i\alpha}^{\dag}c_{j\alpha}+ \tau_{2}\sum_{\langle \gamma\delta\rangle\alpha}c_{i_{y}\alpha,\gamma}^{\dag}c_{i_{y}\alpha,\delta}+ \ 타우_{1}\sum_{\langle i,\gamma\rangle\alpha}c_{i\alpha}^{\dag}c_{i_{y}\alpha,\gamma}\\ &+&i\frac{t_ {so}}{3\sqrt{3}}\sum_{\langle\langle i,j\rangle\rangle\alpha\beta}\nu_{ij}c^{\dag}_{i\alpha}\sigma_ {\alpha\beta}^{z}c_{j\beta}+\Delta_{z}\sum_{i\alpha}\mu_{i} c_{i\alpha}^{\dag}c_{i\alpha }\\ &+&it_{R}\sum_{\langle i,j\rangle\alpha\beta}c_{i\alpha}^{\dag}(\vec{\sigma}\times\mathrm{\mathbf{ d_{ij}}})^{z}_{\alpha\beta}c_{j\beta}+Hc, \end{배열} $$ (1)
여기서 \(c_{i\alpha }^{\dag }\) 및 \(c_{i_{y}\alpha,\gamma /\delta }^{\dag }\)는 스핀
실리신의 ELD는 y를 따라 엄청나게 확장되는 그림 1a에 나와 있습니다. 방향. y를 따른 격자 구조의 병진 대칭 방향은 k를 나타냅니다. 와 는 보존된 양이며 생성(소멸) 연산자는 푸리에 변환에 따라 다음과 같이 다시 작성할 수 있습니다(스핀 인덱스는 무시됨)[17].
$$\begin{array}{@{}rcl@{}} c_{i}^{\dag}=\sum_{k_{y}}c_{k_{y},i_{x}}e^{- 2ik_{y}i_{y}a},c_{i}=\sum_{k_{y}}c_{k_{y},i_{x}}e^{2ik_{y}i_{y}a}, \\ c_{i_{y},\gamma}^{\dag}=\sum_{k_{y},\gamma}c^{\dag}_{k_{y},\gamma}e^{-2ik_ {y}i_{y}a},c_{i_{y},\gamma}=\sum_{k_{y},\gamma}c_{k_{y},\gamma}e^{2ik_{y}i_ {당신}. \end{배열} $$ (2)그런 다음 Eq.의 Hamiltonian 행렬 1은 \(H=\sum _{k_{y}}H_{k_{y}}\)로 분리되며, 여기서 \(H_{k_{y}}\)는 다음 형식으로 설명될 수 있습니다.
$$ {\begin{정렬} H_{k_{y}}=-\sum_{i}\varphi_{i,1}^{\dag}\hat{T}_{11}\varphi_{i,1} -\sum_{i}\varphi_{i,2}^{\dag}\hat{T}_{22}\varphi_{i,2}\\ -\sum_{i}\varphi_{i,1}^ {\dag}\hat{T}_{12}\varphi_{i,2}-\sum_{i\neq-1}\varphi_{i,2}^{\dag}\hat{T}_{23 }\varphi_{i+\hat{x},1}\\ -\varphi_{\bar{1},2}^{\dag}\hat{T}_{\bar{1}0}\varphi_{0 }-\varphi_{0}^{\dag}\hat{T}_{01}\varphi_{1,1}-\varphi_{0}^{\dag}\hat{T}_{00}\varphi_ {0} -\varphi_{\bar{1},2}^{\dag}\hat{T}_{\bar{1}1}\varphi_{1,1}+hc, \end{정렬}} $$ (3)여기서 \(\varphi _{i,l}^{\dag }=\left [ c_{{{k}_{y}},i,l,A\uparrow }^{\dag }, c_{{{ k}_{y}},i,l,A\downarrow }^{\dag }, c_{{{k}_{y}},i,l,B\uparrow }^{\dag },c_{ {{k}_{y}},i,l,B\downarrow }^{\dag }\right ]\), i 인덱스 세트(i,l )는 슈퍼셀 \((\bar {i}=-i)\) 의 위치를 나타내고, l =1 또는 2는 그림 1b의 점선 직사각형에 표시된 것처럼 슈퍼셀에서 서로 다른 지그재그 사슬을 나타냅니다. \(\hat {T_{ll'}}\)는 각 지그재그 체인의 해밀턴 행렬을 나타냅니다(l =나 ′ ) 슈퍼셀 또는 서로 다른 지그재그 사슬 간의 상호작용(l ≠나 ′ ).
두 계곡 K 및 K ′ 이제 [0,±π에서 캐스팅됩니다. /3아 ] 라인 결함의 삽입으로 인한 것입니다. η의 전송 행렬 (η =케이 /케이 ′ ) 계곡은 일반화된 Landauer 공식[26, 27],
을 사용하여 계산됩니다. $$\begin{array}{@{}rcl@{}} T={\left(\begin{array}{cc} T^{\uparrow\uparrow}_{\eta} &T^{\uparrow\ downarrow}_{\eta} \\ T^{\downarrow\uparrow}_{\eta} &T^{\downarrow\downarrow}_{\eta} \end{array} \right)}=\sum_{i ,j=1}^{8}{ \left(\begin{array}{cc} \vert t_{ij,\eta}^{\uparrow\uparrow}\vert^{2} &\vert t_{ij, \eta}^{\uparrow\downarrow}\vert^{2} \\ \vert t_{ij,\eta}^{\downarrow\uparrow}\vert^{2} &\vert t_{ij,\eta} ^{\downarrow\downarrow}\vert^{2} \end{배열} \right)}, \end{배열} $$ (4)어디에
$$\begin{array}{@{}rcl@{}} t=2\sqrt{-Im\Sigma_{L}}G^{r}\sqrt{-Im\Sigma_{R}} \end{array } $$ (5)그리고
$$\begin{array}{@{}rcl@{}} t_{ij,\eta}^{\uparrow\uparrow}&=t_{2(i-1)+1,2(j-1)+ 1}\\ t_{ij,\eta}^{\uparrow\downarrow}&=t_{2(i-1)+1,2j}\\ t_{ij,\eta}^{\downarrow\uparrow}&=t_{2i,2(j-1)+1}\\ t_{ij,\eta}^{\downarrow\downarrow}&=t_{2i,2j}. \end{배열} $$ (6)여기서 \(-Im\Sigma _{L,R}=-\left (\Sigma _{L,R}^{r}-\Sigma _{L,R}^{a}\right)/ 2i\ )은 잘 정의된 행렬 제곱근을 가진 양의 반정부호 행렬입니다. 여기서 \(\Sigma _{L,R}^{a}=\left [\Sigma _{L,R}^{r}\right ]^{ \dag }\)는 왼쪽/오른쪽 리드의 지연/고급 자체 에너지입니다. 16×16 부분행렬 G r x를 따라 첫 번째 슈퍼셀과 마지막 슈퍼셀을 연결하는 지연된 Green의 함수입니다. 방향이며 재귀적 Green의 함수 방법을 사용하여 계산할 수 있습니다. η의 총 투과 계수 계곡은 \(T_{\eta }=T^{\uparrow \uparrow }_{\eta }+T^{\uparrow \downarrow }_{\eta }+ T^{\downarrow \uparrow }_{\eta입니다. }+T^{\downarrow \downarrow }_{\eta }\) 및 스핀 편극 P s 및 계곡 편파 P η 제공할 수 있습니다.
$${\begin{정렬} P_{s}&=\frac{T_{K}^{\uparrow\uparrow}+T_{K}^{\uparrow\downarrow}-T_{K}^{\downarrow\ 아래쪽 화살표}-T_{K}^{\downarrow\uparrow}+T_{K'}^{\uparrow\uparrow}+T_{K'}^{\uparrow\downarrow}-T_{K'}^{\downarrow \downarrow}-T_{K'}^{\downarrow\uparrow}}{T_{K}+T_{K^{\prime}}},\\ P_{\eta}&=\frac{T_{K} -T_{K^{\prime}}}{T_{K}+T_{K^{\prime}}}. \end{정렬}} $$스핀 종속 전송 계수 계산에서 τ를 설정합니다. 2 =τ 1 =그 =1 에너지 단위, SOC 강도 t 그래서 =0.005그 , 페르미 에너지 E f =1.001그 그래서 , 전도대의 하단에 위치합니다. 산란 영역의 너비는 W입니다. 단일 라인 결함의 경우 =1000이고 추가 너비 WR=1000은 그림 1a와 같이 두 개의 평행 라인 결함에 대해서도 고려됩니다.
그림 2는 사건의 함수로서 계곡 \(\eta, T^{sc}_{\eta }/T^{sf}_{\eta }\)의 스핀 보존/스핀 플립 투과 계수를 보여줍니다. 각도 α (a) RSOC 강도 t R (b–d). 그림 2a–c는 단일 라인 결함의 경우에 해당하고 (d)는 두 개의 평행 라인 결함의 경우입니다. 확실한 t에서 R (예:t R =5그 그래서 그림 2a)에서와 같이 스핀 종속 투과 계수 \(T^{sc}_{K}/T^{sf}_{K}\)는 일정하고 포물선 분산 관계로 인해 입사각과 무관합니다. , 도 2a에 도시된 바와 같이. 따라서 다음 계산에서 입사각 α를 사용할 수 있습니다. =0을 예로 들 수 있습니다. 약한 t R , 2차원 전자 가스에서와 유사한 진동 현상[26, 27]이 그림 2b의 삽입 그림에서 볼 수 있듯이 Rashba 분할로 인해 나타납니다. t R 증가(t R >그 그래서 ), \(T_{K}^{\uparrow \uparrow }\) 및 \(T_{K}^{\uparrow \downarrow }\)는 진동 주기가 동일하고 크기가 t R 일부 진동 피크와 최저점으로 구성되어 있는 반면 \(T_{K}^{\downarrow \downarrow }/T_{K}^{\downarrow \uparrow }\) 는 페르미 에너지가 갭에 있기 때문에 0이 되는 경향이 있습니다. 그림 2b에 나와 있습니다. 따라서 K의 총 투과 계수는 밸리는 주로 스핀업 상태에 기여합니다. 실제로 두 계곡의 진동 이미지 K 및 K ′ , K의 투과 계수가 일치하는 동안 ′ 계곡은 주로 스핀다운 전자에 의해 기여됩니다.
<그림>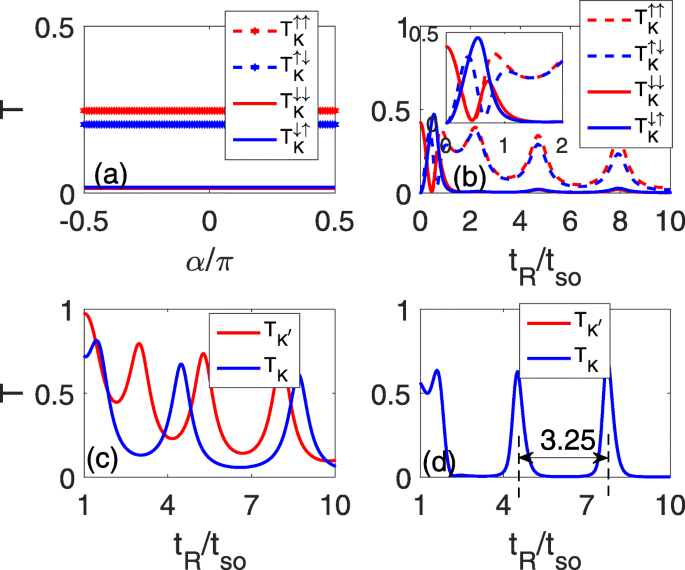
입사각 α의 함수로서의 스핀 보존 및 스핀 플립 투과 계수 t에 R =5그 그래서 a에서 RSOC 강도 t의 기능으로 R b에서 –d , 여기서 a -ㄷ 단일 라인 결함 및 d에 대한 것입니다. Δ와 함께 두 개의 평행선 결함에 대한 것입니다. z =0.2t 그래서 c에서
수직 전기장이 존재하면 계곡 축퇴가 해제되고 두 계곡의 진동 동작이 다릅니다. K의 진동 주기 계곡이 증가하는 반면 K ′ 그림 2c와 같이 계곡이 감소합니다. 그러나 진동하는 바닥이 명확한 크기를 갖기 때문에 단일 라인 결함으로 하나의 원추형 밸리 상태를 필터링하는 것은 불가능해 보입니다. 당연히 그림 2d와 같이 전송을 더욱 억제하기 위해 두 개의 평행선 결함이 있는 진동 현상을 고려할 수 있습니다. 그림 2b와 d를 비교하면 진동 피크가 좁아지고 예각화되는 반면 진동 최저점은 넓어지고 약해져서 제로 전송 플랫폼을 형성함을 알 수 있습니다. 두 개의 인접한 진동 피크 사이의 공간은 3.25t로 고정됩니다. 그래서 , 그림 2d의 두 개의 점선으로 특징지어집니다.
더 나은 밸리 필터 효과를 얻기 위해 수직 전기장의 효과에 주의를 집중합니다. 이 효과의 결과는 그림 3에 나와 있습니다. 위에서 논의한 바와 같이 두 골의 진동 주기는 반대 방식으로 변경되고 그림 2d의 원래 겹치는 진동 피크가 완화됩니다. 한편, 제로 전송 고원은 T에 대해 넓어지고 좁아집니다. 케이 및 \(T_{K^{\prime }}\), 각각 그림 3a 및 b에 표시된 대로. Δ에서 z =0.15t 그래서 , 두 개의 인접한 진동 피크 사이의 공간은 3.6t로 발전합니다. 그래서 T를 위해 케이 , 3.1t로 축소됩니다. 그래서 \(T_{K^{\prime }}\)의 경우 그림 3a에 표시된 두 개의 파란색 및 빨간색 파선으로 표시됩니다. 전기장이 강화됨에 따라 두 개의 인접한 진동 피크 사이의 공간은 T 동안 계속 증가/감소합니다. 케이 /\(T_{K^{\prime }}\), 5.4t 그래서 /2.8t 그래서 Δ에서 z =0.3t 그래서 , 도 3b에 도시된 바와 같이. 진동 주기의 변화는 P가 있는 완벽한 계곡 분극이 있는 넓은 피크-제로 고원의 해당 영역으로 이어질 것입니다. η 그림 3c 및 d에서와 같이 =±1 고원을 실현할 수 있습니다. 동시에 높은 스핀 분극 P s P일 때도 발생합니다. η =±1.
<그림>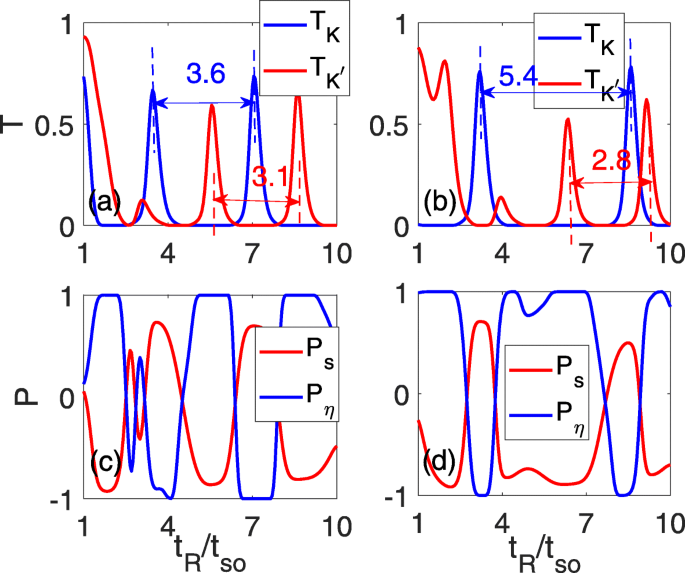
총 투과 계수 \(T_{K}/T_{K^{\prime }}\) (a , b ) 및 스핀/밸리 편광(c , d ) RSOC 강도 t의 함수 R 다른 하위 격자 전위에 대해. Δ z =0.15t 그래서 a에서 및 c 및 Δ z =0.3t 그래서 b에서 그리고 d; 다른 매개변수는 그림 2d의 매개변수와 동일합니다.
그러나 RSOC의 제어 불가능성으로 인해 라인 결함에서 유도된 RSOC가 고유 SOC보다 클 수 있음에도 불구하고 이러한 순수한 밸리 전류를 실험적으로 감지하는 것은 여전히 어렵습니다. 순수 계곡 전류를 실험적으로 편리하게 조사하기 위해 실험 중에 지속적으로 제어할 수 있는 전기장의 함수로서 투과 계수와 계곡 분극도 조사합니다. P에 의한 완벽한 계곡 편파가 나타난다. η =±1은 Δ의 특정 범위에서 나타날 수 있습니다. z P에서 변경할 수 있습니다. η =1 ~ P η 그림 4a와 같이 전기장이 증가함에 따라 =-1입니다. 확실한 t R (예를 들어 t R =7.2t 그래서 , 그림 4a)에서 점선으로 표시된 것처럼 투과 계수 \(T_{K}/T_{K^{\prime }}\)는 Δ로 진동합니다. z , 여기서 K의 넓은 전송 피크 (케이 ′ ) 계곡은 K의 제로 전송 고원에 해당합니다. ′ (케이 ) 계곡. 총 투과 계수는 기본적으로 전기장이 변화함에 따라 하나의 계곡에 의해 기여되며, 그림과 같이 완전한 계곡 분극은 \(T_{K}/T_{K^{\prime }}\)의 최대값 부근에서 항상 발생할 수 있습니다. 그림 4b. 페르미 에너지가 대역 가장자리에서 출발하기 때문에 완벽한 계곡 분극은 E에서도 여전히 생존할 수 있습니다. f =1.5t 그래서 , 그림 4c와 같이 고원 관계가 잘 유지될 수 있습니다. 실험 중에 총 전송 계수에 비례하는 전도도와 같은 실험적으로 측정 가능한 양으로 왼쪽에서 오른쪽 리드로 밸리 분극 전류를 분석할 수 있습니다. 두 최소값(때로는 0임) 사이의 최대 전도도는 한 계곡에서 나와야 합니다. 다음 공식에 따라 컨덕턴스의 크기를 추정할 수 있습니다. \(G=\frac {e^{2}}{h}\int _{-k_{F}}^{k_{F}}T\frac {dk_ {y}}{2\pi /L_{y}}=\frac {e^{2}}{h}\frac {Ly\sqrt {E^{2}-t^{2}_{so}} }{2\pi \hbar v_{F}}2T\) [28], 여기서 L 와 =2a ≈7.72Å는 실리신 라인 결함의 폭, v F =5.5×10 5 나 /s 는 페르미 속도, \(\hbar =h/2\pi \)는 \(\phantom {\dot {i}\!}h=4.13566743\times 10^{-15}eV\cdot를 사용하여 축소된 플랑크 상수입니다. s, T=T_{K}+T_{K'}\) 총 투과 계수 및 E 는 입사 전자의 현장 에너지입니다. 그러면 컨덕턴스는 약 \(G\approx \left [0.7T\sqrt {E^{2}-t^{2}_{so}}/eV\right ]\frac {e^{2}}{ 시간}\). 또한 입사측의 현장 에너지가 E로 상승함을 알 수 있습니다. =0.15t (그 =1.6eV ), 두 골의 투과 계수는 그림 4d와 같이 스핀과 운동량 보존으로 인해 그림 4c에 비해 약간만 변하고 투과 피크-제로 플래토 관계는 여전히 유지됩니다. 이 경우 컨덕턴스는 약 \(G\approx 0.17T\frac {e^{2}}{h}\)이며 실험에서 감지할 수 있습니다. 이 현상을 관찰할 수 있는 에너지 창은 약 0.5t입니다. 그래서 (그 그래서 <이 <1.5그 그래서 ) 이는 t에 비례합니다. 그래서 . 실험에서 밴드 에지 근처에서 페르미 에너지를 제어하는 것은 어렵지 않으며 SOC 갭은 Bi(111) 이중층[29]에 근접하여 44 meV까지 급격하게 증가할 수 있습니다. 이는 순수 검출을 위한 에너지 영역을 크게 향상시킬 수 있습니다. 계곡류. 또한, 계산 모델은 그래핀, 게르마넨[30], stanene 및 MoS2의 다른 낮은 버클 대응물에도 적용할 수 있습니다. [31-36], 더 큰 밴드 갭[37, 38]과 SOC 강도(SOC 강도는 stanene의 경우 0.1eV에 도달할 수 있음[38, 39])가 있습니다. 실제 실험에서는 특수 기판으로 면내 거울 대칭을 깨뜨리면 고유 SOC를 초과할 수 있는 강한 RSOC를 쉽게 실현할 수 있다[40]. 따라서 이 계획은 실험에서 완전히 실현 가능합니다.
<그림>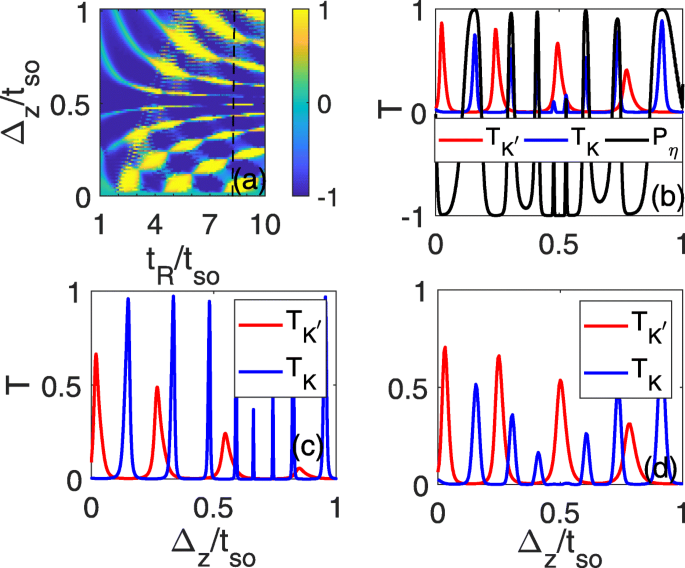
계곡 양극화 a 및 \(T_{K}/T_{K^{\prime }}\) (b –d ) Δ의 함수로 z 그리고 t R . 그 R =7.2t 그래서 (b에서 –d ), E f =1.5t 그래서 c에서 그리고 d , 현장 에너지는 E입니다. =0.15t d의 왼쪽 전극에; 다른 모든 매개변수는 그림 2d의 매개변수와 동일합니다.
우리는 실리신 라인 결함에서 밸리 분극 전류를 생성하는 전기적 방법을 제안했습니다. 밸리 분극 전류를 생성하는 데 사용되는 기존의 전기적 접근 방식과 극명하게 대조적으로, 우리는 스핀 분극 FET에서 널리 사용되는 스핀 분극을 조정하는 것으로 간주되는 RSOC를 탐구합니다. 두 계곡의 투과 계수는 투과 피크와 제로 투과 고원으로 구성된 동일한 주기와 강도로 진동하는 것으로 나타났습니다. 계곡 편극 전류는 전기장으로 두 계곡의 진동 주기를 조정하여 생성할 수 있으며, 이는 계곡 상태의 대칭을 파괴하고 해당 전송 피크-제로 고원 영역을 가져올 수 있습니다. 또한, 우리는 실험에서 순수한 밸리 전류를 감지하는 방식을 제공하고 그 결과는 전기 수단에 의한 밸리 편광 전류의 조작에 빛을 비출 수 있습니다.
현재 연구 중에 생성 및/또는 분석된 데이터 세트는 합당한 요청이 있는 경우 해당 저자로부터 사용할 수 있습니다.
2차원
확장된 라인 결함
전계 효과 트랜지스터
Rashba 스핀-궤도 결합
고유 스핀-궤도 커플링
나노물질
완성된 부품에 결함이나 흠집이 있으면 분명히 불만족스러운 사람이 될 것입니다. 플라스틱으로 만든 부품의 경우 흠집이 부품의 기능적 장애로 이어질 수 있으므로 더 많은 문제를 의미할 수 있습니다. 플라스틱 부품의 이러한 흠집의 예로는 웰드 라인이 있습니다. 이 라인은 전체 생산 공정의 실패로 이어질 수 있으므로 플라스틱 제품에 심각한 영향을 줄 수 있습니다. 이것은 일반적으로 프로세스가 처음부터 다시 시작되어야 하므로 막대한 돈의 손실을 의미합니다. 이를 방지하기 위해 이 기사에서는 웰드 라인의 원인과 그로 인한 결함 및 방지 방법
분말 코팅은 금속, 플라스틱 및 기타 재료에 사용할 수 있는 가장 널리 사용되는 마무리 기술 중 하나입니다. 내구성이 뛰어나고 비용 효율적이며 다재다능합니다. 페인트 대신 분말 코팅 솔루션을 선택하는 것은 종종 제조 및 제조 회사에게 쉬운 결정이지만 기업은 시스템에 투자하기 전에 다른 결정을 내려야 합니다. 그들은 수동 또는 자동 분말 코팅 솔루션을 선택해야 합니다. 자동화된 분말 코팅 라인은 품질 저하 없이 빠른 처리 시간에 보조를 맞춰야 하는 회사에 많은 이점을 제공합니다. 자동 분체 도장 라인의 이점 수동 분말 코팅 스프레