더 큰 5 및 6-변수 Karnaugh 지도

더 큰 Karnaugh 맵은 더 큰 논리 설계를 줄입니다. 얼마나 큰 것이 충분히 큰가? 입력 수, 팬인에 따라 다릅니다. , 고려중인 논리 회로에. 대형 프로그래머블 로직 회사 중 하나에 답이 있습니다.

알테라의 고객 디자인 라이브러리에서 추출한 자체 데이터는 이질성의 가치를 뒷받침합니다. 로직 콘을 조사하고 LUT 기반 노드에 매핑하고 각 노드에서 가장 좋은 입력 수에 따라 정렬함으로써 Altera는 팬 인 분포가 2개에서 6개 입력 사이에서 거의 평평하다는 것을 발견했습니다. 5시에.

대답은 대부분의 모든 설계에 대해 6개 입력, 평균 로직 설계에 대해 5개 입력입니다. 5가지 변수 Karnaugh 지도가 다음과 같습니다.

5가지 변수 K-맵

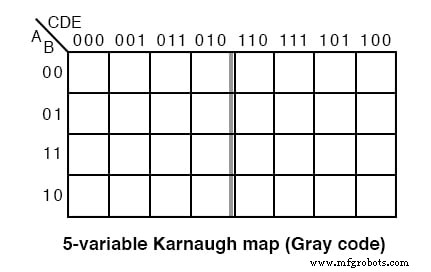
5가지 변수 K-맵의 이전 버전인 그레이 코드 맵 또는 반사 맵이 위에 표시됩니다. 지도의 상단(6변수 맵의 경우 측면)은 전체 그레이 코드로 번호가 매겨집니다. 그레이 코드는 코드의 중간 정도를 반영합니다. 이 스타일 지도는 오래된 텍스트에서 찾을 수 있습니다. 새로운 선호 스타일은 아래와 같습니다.

K-map의 오버레이 버전

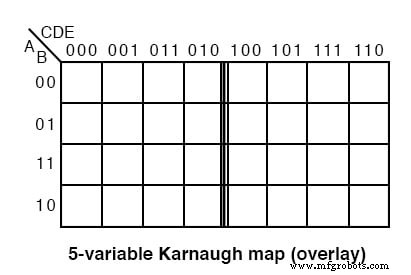
위에 표시된 Karnaugh 맵의 오버레이 버전은 상단에 있는 3비트 주소의 최상위 비트를 제외하고 단순히 두 개(6변수 맵의 경우 4개)의 동일한 맵입니다.

맵 상단을 보면 기존 그레이 코드 맵과 넘버링이 다르다는 것을 알 수 있습니다. 3자리 숫자 중 최상위 숫자를 무시하면 시퀀스 00, 01, 11, 10 오버레이 맵의 두 하위 맵의 머리글에 있습니다. 8자리 3자리 숫자의 시퀀스는 그레이 코드가 아닙니다. 최하위 2비트 중 4개의 시퀀스는 다음과 같습니다.

5-변수 Karnaugh Map을 사용하도록 합시다. A가 MSB(Most Significant Bit)인 5비트 이진 입력(A, B, C, D, E)이 있는 회로를 설계하십시오. 입력 데이터에서 감지된 모든 소수에 대해 출력 논리 High를 생성해야 합니다.

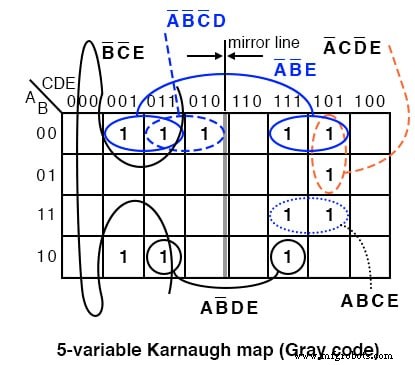
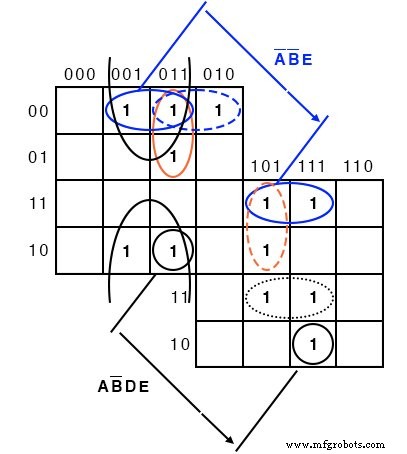
참조용으로 이전 그레이 코드(반사) 맵에 위의 솔루션을 표시합니다. 소수는 (1,2,3,5,7,11,13,17,19,23,29,31)입니다. 플롯 1 각 해당 셀에서. 그런 다음 셀 그룹화를 진행합니다. 단순화된 결과를 작성하여 완료합니다.

4셀 그룹 A'B'E는 미러 라인의 양쪽에 있는 두 쌍의 셀로 구성됩니다. 2셀 그룹 AB'DE도 마찬가지입니다. 미러 라인에 반사되어 2셀 그룹입니다. 이 버전의 K-map을 사용할 때 지도의 다른 절반에서 미러 이미지를 찾으십시오.

출력 =A'B'E + B'C'E + A'C'DE + A'CD'E + ABCE + AB'DE + A'B'C'D

아래에서는 5변수 맵의 더 일반적인 버전인 오버레이 맵을 보여줍니다.

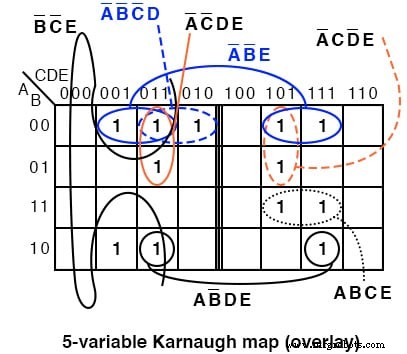
두 맵의 패턴을 비교하면 맵 상단의 주소 지정이 다르기 때문에 맵의 오른쪽 절반에 있는 일부 셀이 이동합니다. 또한 지도의 두 부분 사이의 공통점을 찾는 데 다른 접근 방식을 취해야 합니다.

지도의 절반을 다른 절반 위에 오버레이합니다. 상단 맵에서 하단 맵으로의 모든 겹침은 잠재적인 그룹입니다. 아래 그림은 그룹 AB'DE가 두 개의 스택 셀로 구성되어 있음을 보여줍니다. 그룹 A'B'는 두 개의 적층된 셀 쌍으로 구성됩니다.

A'B'B' 4셀 그룹 ABCDE =00xx1 그룹을 위해. 즉, A,B,E는 동일합니다. 001 그룹별로. 그리고 CD=xx 즉, CD=xx에는 공통점이 없습니다. 4셀 그룹의 경우. ABCDE =00xx1 이후 , 4셀 그룹은 A'B'XXE =A'B'E로 덮여 있습니다. .

위의 5개 변수 오버레이 맵이 스택으로 표시됩니다.

6개의 변수 Karnaugh 맵의 예는 다음과 같습니다. Out =C'F'에 해당하는 4셀 그룹을 보기 위해 4개의 하위 맵을 정신적으로 쌓았습니다.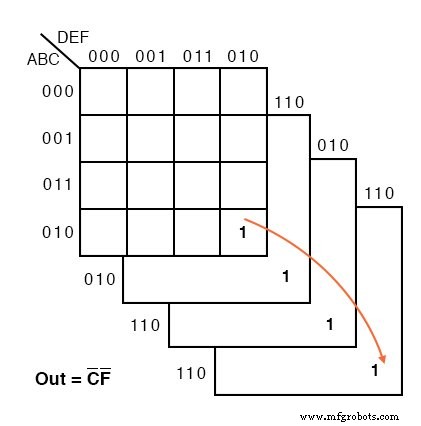

크기 비교기(6변수 K-맵을 설명하는 데 사용됨)는 2개의 이진수를 비교하여 3개의 개별 출력에서 ​​서로 같은지, 큰지 또는 작은지를 나타냅니다. 3비트 크기 비교기에는 두 개의 입력 A₂가 있습니다. A₁ A₀ 및 B₂ B₁ B₀ 집적 회로 크기 비교기(7485)에는 실제로 4개의 입력이 있지만 아래의 Karnaugh 맵은 적절한 크기로 유지해야 합니다. A>B에 대해서만 해결합니다. 출력.

6 가변 K-맵

아래에서 6-변수 Karnaugh 맵은 3비트 크기 비교기에 대한 논리를 단순화하는 데 도움이 됩니다. 오버레이 유형의 지도입니다. 지도의 왼쪽 위와 아래를 가로지르는 바이너리 주소 코드는 완전한 3비트 그레이 코드가 아닙니다.

4개의 서브맵의 2비트 주소 코드는 그레이 코드이지만. 4개의 하위 맵을 서로 겹쳐서 중복 표현식을 찾습니다(위 참조). 아래 예에는 없지만 네 가지 지도 모두에 공통적인 셀이 있을 수 있습니다. 한 쌍의 하위 지도에 공통적인 셀이 있습니다.

위의 A>B 출력은 아래 지도에서 ABC>XYZ입니다.

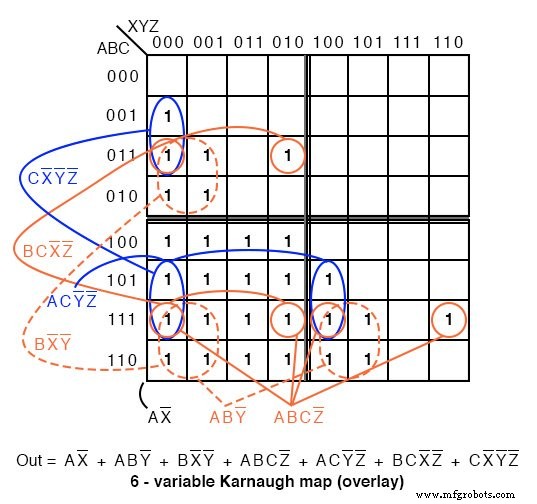
ABC XYZ보다 큽니다. , 1 플롯됩니다. 첫 번째 줄 ABC=000 XYZ 값보다 클 수 없습니다. . 1 없음 이 줄에 s. 두 번째 줄에서 ABC=001 , 첫 번째 셀만 ABCXYZ=001000 ABC입니다. XYZ보다 큼 . 단일 1 두 번째 줄의 첫 번째 셀에 입력됩니다. 네 번째 줄, ABC=010 , 1 쌍이 있습니다. 에스. 세 번째 줄, ABC=011 3개의 1이 있습니다. 에스. 따라서 지도는 1로 채워집니다. ABC가 있는 모든 셀에서 XXZ보다 큽니다. .

셀을 그룹화할 때 가능하면 인접한 하위 맵과 그룹을 형성합니다. 16개의 셀로 구성된 한 그룹을 제외한 모든 그룹에는 하위 맵 쌍의 셀이 포함됩니다. 다음 그룹을 찾으십시오.

<울>

16셀로 구성된 그룹 1개

8셀로 구성된 2개 그룹

4셀 그룹 4개

16셀 그룹, AX' 오른쪽 하단 서브맵 전체를 차지합니다. 하지만 위 그림에서는 동그라미를 치지 않았습니다.

8셀의 한 그룹은 왼쪽 하단 맵의 유사한 그룹을 오버레이하는 상위 서브맵의 4셀 그룹으로 구성됩니다. 8셀의 두 번째 그룹은 왼쪽 하단 지도의 동일한 4셀 그룹을 오버레이하는 오른쪽 서브맵의 유사한 4셀 그룹으로 구성됩니다.

위의 Karnaugh 지도에는 4개의 4셀 그룹이 관련 제품 용어와 함께 표시되어 있습니다. 8셀로 구성된 두 그룹 및 16셀로 구성된 그룹에 대한 제품 항과 함께 최종 Sum-Of-Products 감소가 표시되며, 7개 항 모두가 표시됩니다.

1 세기 맵에는 총 16+6+6=28개가 있습니다. K-map 논리 축소 이전에는 SOP 출력에 28개의 제품 용어가 있었고 각각 6개의 입력이 있었습니다. Karnaugh 지도는 4개 이하의 입력에 대해 7개의 곱 항을 산출했습니다. 이것이 바로 Karnaugh 지도의 모든 것입니다!

배선도는 표시되지 않습니다. 그러나 다음은 4개의 TTL 논리 제품군 부품을 사용하는 ABC>XYZ에 대한 3비트 크기 비교기의 부품 목록입니다.

<울>

7410 트리플 3입력 NAND 게이트 AX', ABY', BX'Y' 1개

2개 7420 듀얼 4입력 NAND 게이트 ABCZ', ACY'Z', BCX'Z', CX'Y'Z'

7-P-term의 출력을 위한 1개 7430 8-입력 NAND 게이트

검토:

<울>

부울 대수학, Karnaugh 지도 및 CAD(Computer Aided Design)는 논리 단순화 방법입니다. 논리 단순화의 목표는 최소 비용 솔루션입니다.

최소 비용 솔루션은 최소 입력 수와 최소 게이트 수로 유효한 논리 감소입니다.

벤 다이어그램을 사용하면 부울 표현식을 시각화하여 Karnaugh 맵으로 쉽게 전환할 수 있습니다.

Karnaugh 지도 셀은 단순화를 초래하는 부울 표현식의 중복성을 시각화할 수 있도록 그레이 코드 순서로 구성됩니다.

더 일반적인 Sum-Of-Products(Sum of Minters) 표현식은 단일 OR 게이트(sum)를 제공하는 AND 게이트(product)로 구현됩니다.

Sum-Of-Products 표현식(AND-OR 논리)은 NAND-NAND 구현과 동일합니다. 모든 AND 게이트와 OR 게이트는 NAND 게이트로 대체됩니다.

덜 자주 사용되는 Product-Of-Sums 표현식은 단일 AND 게이트(곱)에 공급되는 OR 게이트(합)로 구현됩니다. 합산 표현식은 0을 기반으로 합니다. Karnaugh 지도의 s, maxterms.