더 큰 4변수 Karnaugh 지도

그레이 코드를 생성하는 방법을 알면 더 큰 지도를 만들 수 있습니다. 사실, 우리가 해야 할 일은 3-변수 맵의 상단을 가로질러 왼쪽에서 오른쪽 순서로 살펴보고 4-변수 맵의 왼쪽 아래로 복사하는 것입니다. 아래를 참조하십시오.

4개의 변수 K 맵 축소

다음 4개의 변수 Karnaugh 맵은 부울 대수에 대해 너무 지루한 부울 표현식의 감소를 보여줍니다. 부울 대수를 사용하여 줄일 수 있습니다.

그러나 Karnaugh 지도는 특히 수행할 논리 축소가 많은 경우 더 빠르고 쉽습니다.

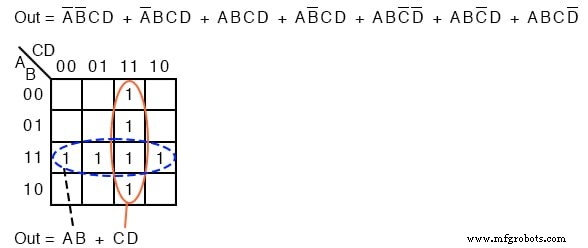
위의 부울 표현식에는 7개의 제품 용어가 있습니다. 위의 K-map에서 위에서 아래로, 왼쪽에서 오른쪽으로 매핑됩니다. 예를 들어 첫 번째 P-term A'B'CD 지도 위치 A=0, B=0, C=1, D=1에 해당하는 첫 번째 행, 세 번째 셀입니다. .

다른 제품 용어도 유사한 방식으로 배치됩니다. 가능한 가장 큰 그룹을 둘러싸면 4명씩 2개 그룹이 위에 표시됩니다.

점선 가로 그룹은 단순화된 제품 용어 AB에 해당합니다. . 수직 그룹은 부울 CD에 해당합니다. 두 그룹이 있으므로 Out=AB+CD의 Sum-Of-Products 결과에 두 개의 제품 항이 있습니다. .

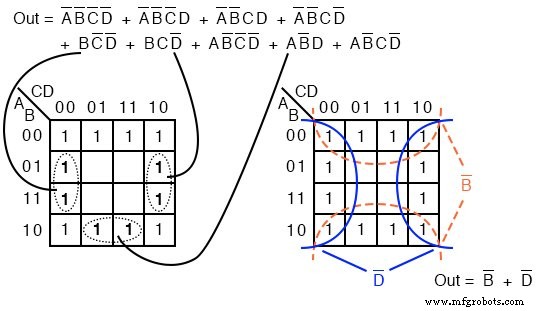
4개의 셀이 물리적으로 인접하도록 아래 지도의 모서리를 냅킨처럼 접습니다.

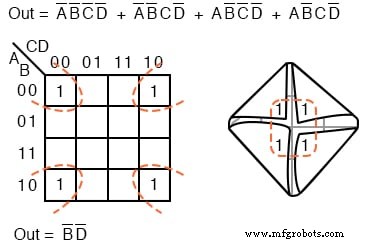
위의 4개 셀은 모두 부울 변수 B'를 갖기 때문에 4개의 그룹입니다. 및 D' 공통점. 즉, B=0 4개의 셀에 대해 D=0 4개의 셀에 대해.

기타 변수 (A, C) 0입니다. 경우에 따라 1 네 모서리 셀과 관련하여 다른 경우.

따라서 이러한 변수는 (A, C) 이 4인조 그룹과 관련이 없습니다. 이 단일 그룹은 단순화된 결과에 대한 하나의 제품 용어로 지도에서 나옵니다. Out=B'D'

아래 K-map의 경우 위쪽 및 아래쪽 가장자리를 8개의 인접한 셀을 형성하는 원통으로 굴립니다.

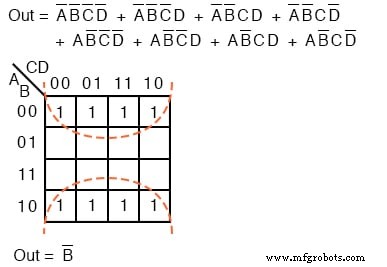
위의 8개 그룹에는 하나의 공통 부울 변수가 있습니다. B=0 . 따라서 8명으로 구성된 한 그룹은 하나의 p-term인 B'에 적용됩니다. . 원래의 8항 부울 표현식은 Out=B'로 단순화됩니다.

4 변수 K 맵의 P-항

아래의 부울 표현식에는 9개의 p-항이 있으며 그 중 3개에는 4개가 아닌 3개의 부울이 있습니다. 차이점은 4개의 부울 변수 곱 항이 하나의 셀을 포함하는 반면 3개의 부울 p-항은 각각 한 쌍의 셀을 포함한다는 것입니다.

4개의 부울 변수에 대한 6개의 곱 항은 위의 일반적인 방식으로 단일 셀로 매핑됩니다. 3개의 부울 변수 용어(각각 3개)는 위에 표시된 것처럼 셀 쌍으로 매핑됩니다.

p-term을 K-map에 매핑하는 중이지 이 ​​시점에서 빼지 않습니다.

단순화를 위해 8명씩 두 그룹을 구성합니다. 모서리에 있는 셀은 두 그룹과 공유됩니다. 이건 괜찮아. 사실, 이것은 셀을 공유하지 않고 8인 그룹과 4인 그룹을 형성하는 것보다 더 나은 솔루션으로 이어집니다. 최종 솔루션은 Out=B'+D'입니다.

아래에서 단순화되지 않은 부울 표현식을 Karnaugh 맵에 매핑합니다.

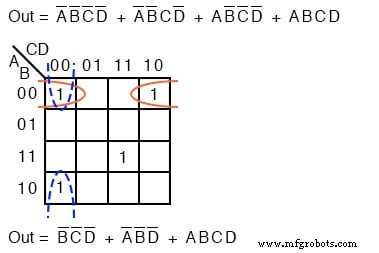
위에서 3개의 세포가 2개의 세포로 이루어진 그룹을 형성합니다. 네 번째 셀은 "실제 세계" 문제에서 자주 발생하는 어떤 것과도 결합할 수 없습니다. 이 경우 부울 p항 ABCD 단순화 프로세스에서 변경되지 않습니다. 결과:아웃=B'C'D'+A'B'D'+ABCD

종종 단순화 문제에 대한 하나 이상의 최소 비용 솔루션이 있습니다. 아래 그림과 같은 경우입니다.

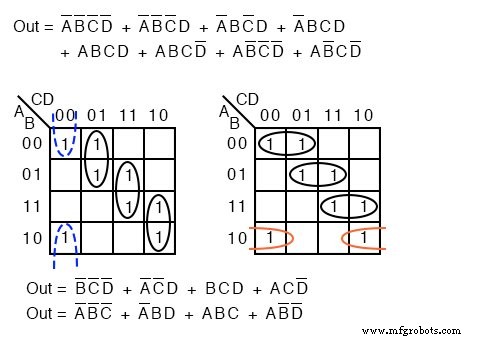
위의 두 결과에는 각각 3개의 부울 변수에 대한 4개의 곱 항이 있습니다. 둘 다 동일하게 유효합니다. 최소 비용 솔루션. 최종 솔루션의 차이는 위와 같이 셀을 그룹화하는 방식 때문입니다.

최소 비용 솔루션은 최소 입력 수와 최소 게이트 수를 가진 유효한 논리 설계입니다.

아래에서 우리는 평소와 같이 단순화되지 않은 부울 방정식을 매핑하고 첫 번째 단순화 단계로 4개의 그룹을 형성합니다. 남아있는 세포를 어떻게 선택해야 하는지 명확하지 않을 수 있습니다.

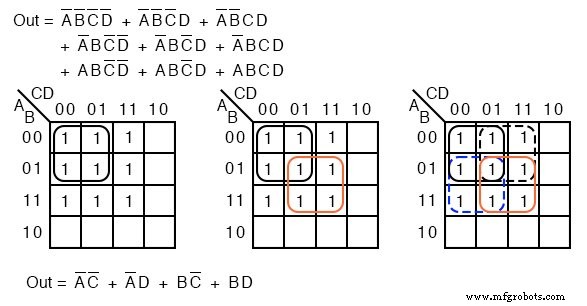
위 중앙의 4개 그룹에서 3개의 셀을 더 선택합니다. 아직 두 개의 셀이 남아 있습니다. 이들을 선택하는 최소 비용 방법은 위의 오른쪽과 같이 인접 셀과 4개의 그룹으로 그룹화하는 것입니다.

주의할 점은 3명으로 구성된 그룹을 만들지 마십시오. 그룹화는 2의 거듭제곱, 즉 1, 2, 4, 8 ...

이어야 합니다.

아래에는 두 가지 가능한 최소 비용 솔루션의 또 다른 예가 있습니다. 세포를 매핑한 후 4명씩 두 그룹을 형성하여 시작하십시오.

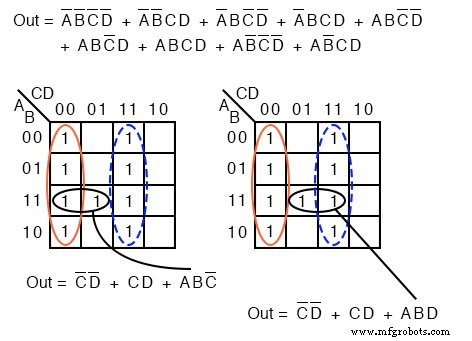
두 가지 솔루션은 남아 있는 단일 셀이 두 셀의 그룹으로 첫 번째 또는 두 번째 그룹 4개와 함께 그룹화되는지 여부에 따라 다릅니다. 해당 셀은 ABC'로 나옵니다. 또는 ABD , 당신의 선택.

어느 쪽이든, 이 셀은 부울 곱 용어 중 하나에 포함됩니다. 최종 결과는 위에 나와 있습니다.

아래에는 왼쪽의 Karnaugh 맵 또는 오른쪽의 부울 대수학을 사용한 단순화의 예가 있습니다. 플롯 C' 지도에서 주소 C=0이 포함된 모든 셀 영역 , 지도 왼쪽의 8셀. 그런 다음 단일 ABCD를 플로팅합니다. 셀.

이 단일 셀은 그림과 같이 2셀 그룹을 형성하며 이는 P-term ABD로 단순화됩니다. , Out =C' + ABD의 최종 결과 .

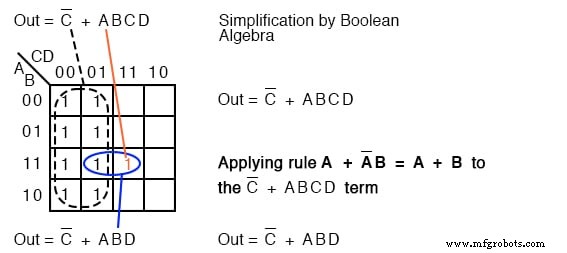
이것은 (위) 당신이 정리를 기억한다고 가정할 때 많은 노력 없이 부울 대수로 줄일 수 있는 4변수 문제의 드문 예입니다.

관련 워크시트:

<울>

Karnaugh 매핑 워크시트