나노물질








이 연구는 메타표면 편광자의 열화 특성에 대한 실험적 및 수치적 조사에 중점을 둡니다. 메타표면은 근적외선 영역에서 10,000 정도의 높은 소광비를 나타내는 적층된 보완 구조를 가지고 있습니다. 그러나 시간이 지남에 따라 성능이 크게 저하되었습니다. 이러한 열화의 원인을 명확히 하기 위해 표면 거칠기와 금속 손실의 영향을 수치적으로 조사했습니다. 열화는 주로 손실 증가에 기인합니다. 이러한 수치 계산은 또한 상보 구조의 두께를 다른 값으로 조정함으로써 소광비가 향상됨을 보여줍니다. 본 연구는 시간 열화에 대한 민감도가 낮고 소광비가 높은 메타표면 편광판을 구현하는 길을 열었다.
<섹션 데이터-제목="배경">나노크기의 빛 제어는 나노광학 및 나노포토닉스 분야에서 널리 연구되어 왔다. 그 결과 지금까지 다양한 형태의 광자나노구조가 제안되었다. 예를 들어, 초고품질(Q) 인자[1]를 가진 광결정(PhC) 나노공동은 빛을 파장 이하 영역으로 가둘 수 있습니다. PhC 공동과 유사하게 높은 Q 계수는 마이크로 디스크[2, 3], 구형[4] 및 트로이달[5] 공동에 의해 실현됩니다. 높은 Q 계수를 가진 공동은 일반적으로 투명한 유전 물질로 구성됩니다. 이러한 유전 공동과 달리 금속 공동은 Q 계수가 낮지만 전체 공동 크기를 줄일 수 있습니다. 특히, 플라즈몬 서브파장 공동은 극히 작은 규모의 빛을 제어하는 데 중요합니다[6]. 플라즈몬 공동은 낮은 Q 계수를 갖지만 깊은 하위 파장 영역으로 빛을 압축할 수 있습니다[7]. 이 극도로 제한된 빛은 포토닉스와 전자공학을 결합하는 열쇠가 될 것으로 예상됩니다[8].
위에서 언급한 광자 나노구조 외에도 메타표면은 최근 고기능성 및 초박형 광학소자를 설계하기 위해 상당한 주목을 받고 있다. 굴절[9], 반사[10], 광발광[11], 형광[12-14], 파장판[15] 및 빔 스플리터[16]를 제어하는 다양한 유형의 메타표면이 있습니다. 편광 상태는 메타표면에 의해 제어될 수 있는 빛의 기본적이고 중요한 속성 중 하나입니다[17-22]. 수치적 및 실험적 연구에 따르면 적층된 상보적 구조를 갖는 메타표면 편광자는 근적외선 영역에서 10,000 정도의 높은 소광비를 갖는다[23-26]. 상보적 구조는 Babinet의 원리로 인해 거의 동일한 파장에서 공명을 가집니다[27, 28]. 상보적 구조가 특정 편광에 대해 높은 투과율을 나타내는 공진 상에 있을 때, 다른 구조는 동일한 편광에 대해 낮은 반사율을 나타내는 오프 공진입니다. 그 결과, 전체 구조가 높은 투과율을 나타냅니다. 직교 편광의 경우 전기장과 자기장의 역할이 교환되어 높은 반사율이 발생합니다. 따라서 상보적인 구조를 가진 메타표면은 높은 소광비를 보인다. 그러나 메타표면이 대기에서 분해되는 은을 포함하기 때문에 이 고성능의 안정성과 신뢰성에 대해 깊은 우려가 있습니다. 이 문제를 피하기 위해 대안적인 접근 방식은 금을 플라즈몬 재료로 사용하는 것이지만 이는 금속 손실 증가로 인해 편광판의 성능을 저하시킵니다. 따라서 실제 적용을 위해서는 메타표면 편광자의 안정성과 신뢰성을 다루어야 합니다.
이 연구에서는 메타표면 편광판의 열화 특성을 조사합니다. 우리는 편광판의 소광비가 시간 열화를 나타냄을 보여줍니다. 열화의 원인으로 우리는 편광판의 고성능에 대한 표면 형태의 영향에 중점을 둡니다. 형태를 설명하기 위해 두 가지 모델을 소개합니다. 하나는 가우시안 백색 잡음이 있는 주기적인 곡선으로 표면 거칠기를 설명하고 다른 하나는 무작위로 분포된 나노 입자를 사용하여 거칠기를 설명합니다. 우리는 또한 고성능에 대한 금속 손실의 영향을 조사했습니다. 이러한 수치 계산을 통해 우리는 열화를 일으키는 중요한 요소를 밝히고 높은 소광비를 가진 최적화된 메타표면 편광자를 제안합니다.
높은 소광비 측정을 위한 실험 설정은 그림 1에 개략적으로 나와 있습니다. 우리는 주파수 3배의 Nd:YAG(yttrium iron garnet) 레이저(Optolette 355, Opotek)에 의해 펌핑된 광학 매개변수 발진기(OPO)를 빛으로 사용했습니다. 원천. 펄스 폭과 반복률은 각각 7ns와 20Hz였다. OPO의 아이들러 빛은 렌즈로 샘플에 초점을 맞추고 GLP(Glan-laser prism)에 의해 선형 편광되었습니다. 투과된 아이들러 광은 확장된 InGaAs 광검출기(Edmund Optics)에 의해 측정되었습니다. 이 광학 시스템에서 단일 펄스의 광 강도 변동은 신호 대 잡음비(S/N)를 불량하게 만듭니다. 따라서 이러한 변동의 영향을 제거하기 위해 단일 펄스의 평균 투과율을 측정했습니다. 단일 펄스의 광도를 모니터링하기 위해 렌즈와 GLP 사이에 한 쌍의 빔 샘플러를 삽입했습니다. 아이들러 광의 일부는 두 번째 빔 샘플러(BS2)에서 반사된 다음 반사 중성 밀도(ND) 필터에서 다시 반사되어 광검출기를 손상시키지 않도록 반사된 레이저 강도를 조정했습니다. 조정된 레이저는 핀홀을 통해 확장된 InGaAs 광검출기(Edmund Optics)에 입사하여 BS2의 후면에서 반사된 불필요한 "고스트" 빛을 차단했습니다(그림 1 삽입 참조). 첫 번째 빔 샘플러는 광학 경로의 편차를 보정하는 역할을 합니다.
<그림>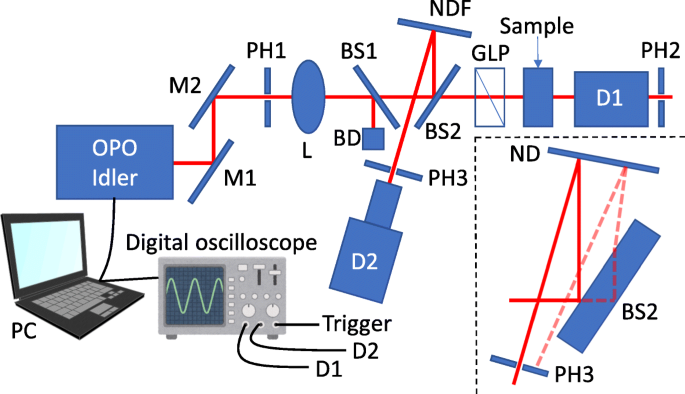
소광비 측정의 실험 설정의 개략도. M 미러, PH 핀홀, L 렌즈, BS 빔 샘플러, BD 빔 댐퍼, NDF 중성 밀도 필터, GLP Glan-레이저 프리즘, D 검출기
이 설정을 사용하여 다음과 같이 소광비를 평가했습니다. 전송된 신호는 D로 계산됩니다. 1 =(1−R BS2 )T GLP 티 샘플 나 , 여기서 R BS2 , T GLP , T 샘플 , 그리고 나 BS2의 반사율, GLP의 투과율, 샘플의 투과율, BS2 전면의 광도입니다. 검출기 2의 신호 강도는 D로 계산됩니다. 2 =R BS2 R NDF 나 , 여기서 R NDF 반사 ND 필터의 반사율입니다. 검출된 신호가 광량에 비례하도록 광량을 충분히 감소시킨다는 점에 유의하십시오. D 사용 1 그리고 디 2 , 우리는 T를 계산할 수 있습니다. 샘플
로 $$\begin{array}{@{}rcl@{}} T_{\text{샘플}} =\frac{R_{\mathrm{BS2}}R_{\text{NDF}}}{1-R_{ \mathrm{BS2}}}\frac{1}{T_{\text{GLP}}}\frac{D_{1}}{D_{2}}. \end{배열} $$ (1)T를 평가하려면 샘플 , 우리는 또한 빔 샘플러와 같은 광학 요소의 반사율과 투과율을 측정해야 합니다. 우리의 초점이 소광비, 즉 투과율에 있기 때문에 이것은 불필요합니다. 샘플을 90° 회전하고 동일한 설정으로 투과율을 측정하면 간단히 소광비 η를 얻을 수 있습니다.
로 $$\begin{array}{@{}rcl@{}} \eta =\frac{T_{\text{샘플}}^{\mathrm{H}}}{T_{\text{샘플}}^{ \mathrm{L}}} =\frac{(D_{1}/D_{2})^{\mathrm{H}}}{(D_{1}/D_{2})^{\mathrm{L} }}, \end{배열} $$ (2)여기서 위 첨자 H와 L은 각각 높은 투과율과 낮은 투과율을 나타내는 편광 상태를 나타냅니다. 이 논문에서는 D 비율을 측정했습니다. 1 /디 2 직교 편광 상태에 대해 소광비 η를 평가했습니다. .
측정된 데이터의 유효성을 확인하기 위해 산란행렬법[29, 30]과 역푸리에법[31]을 통합한 엄밀한 결합파 분석(RCWA)을 기반으로 수치 계산을 수행했습니다. Ag와 실리카의 유전율은 각각 [32]와 [33]에서 얻었다. 계산에 사용된 역격자 벡터의 수는 2601입니다.
거친 금속 구조의 투과율을 계산하기 위해 유한 요소법에 기반한 COMSOL Multiphysics의 상용 소프트웨어를 사용했습니다. 이전 연구[34]에서 광학 응답에 대한 거칠기의 영향은 금속 유전율의 허수부의 증가로 설명되었습니다. 본 논문에서는 금속 손실의 증가와 함께 투과율에 대한 거칠기에 따른 구조적 변화의 직접적인 영향도 고려하였다. 우리는 이 두 가지 효과를 따로따로 다루었습니다. 구조적 변화의 영향만을 고려할 때, 거칠기를 갖는 금속 구조에 벌크 유전율을 적용하였다. 한편, 증가된 손실의 영향만을 고려할 때, 거칠기가 없는 금속 구조에 수정 유전율을 적용하였다. 수치 계산의 상대 허용 오차를 1% 미만으로 설정했습니다.
그림 2a는 3층 메타표면 편광판의 개략도를 보여줍니다. 첫 번째 층은 세 번째 층(그림 2b 참조)과 상보적인 구조를 가지며 두 층 모두 은(Ag)을 포함합니다. 두 번째 층과 기질은 실리카(SiO2 ). 그림 1c와 같이 메타표면은 직사각형 구멍(150 nm × 540 nm) 쌍의 배열을 가지며 x 그리고 y 지도. 금속층과 유전체층의 두께는 각각 45nm와 200nm입니다(그림 2d 참조). 샘플은 후속 건식 에칭 기술과 결합된 나노임프린트 리소그래피에 의해 준비되었습니다[35]. 샘플 준비에 대한 자세한 내용은 [26]에 설명되어 있습니다. 그림 3은 준비된 시료의 주사전자현미경(SEM) 이미지를 보여줍니다.
<그림>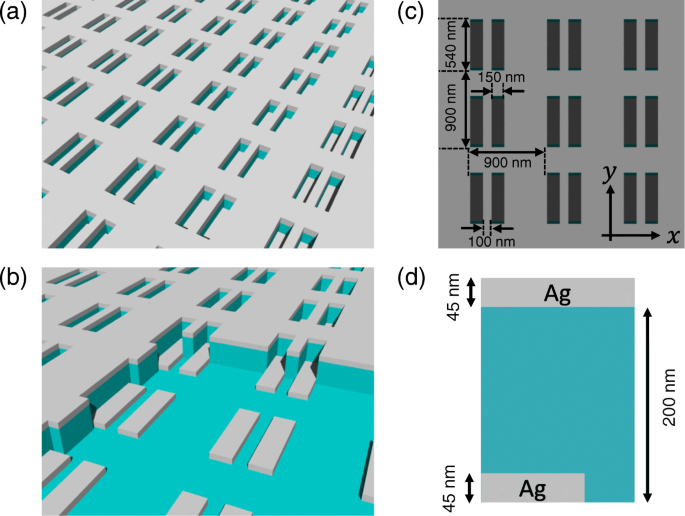
메타표면 편광판의 개략도(a ) 세 개의 레이어(b ). 메타표면은 x 그리고 y 길찾기(c ). 금속 및 유전층의 두께는 각각 45 및 200 nm입니다(d )
<그림>
a의 SEM 이미지 메타표면 편광자와 b 확대된 이미지
분광 광도계(V-7200, JASCO, Japan)를 사용하여 x 샘플의 투과율을 측정했습니다. 그리고 y 양극화. 그림 4는 측정된 결과를 보여줍니다. 파란색과 녹색 선은 x의 투과율을 나타냅니다. 그리고 y 양극화, 각각. 높은 투과율에 해당하는 파란색 선은 높은 신호 대 잡음비로 측정됩니다. 그러나 낮은 투과율에 해당하는 녹색선은 낮은 신호대잡음비를 나타내므로 편광자의 소광비가 높다는 것을 알 수 있다. 특히 녹색선은 투과광의 세기가 분광광도계의 노이즈 레벨 이하이기 때문에 1350nm보다 긴 파장에서 음의 신호를 갖는다. 따라서 우리는 이전 섹션에서 설명한 광학 시스템을 사용하여 높은 소광비를 측정했습니다.
<그림>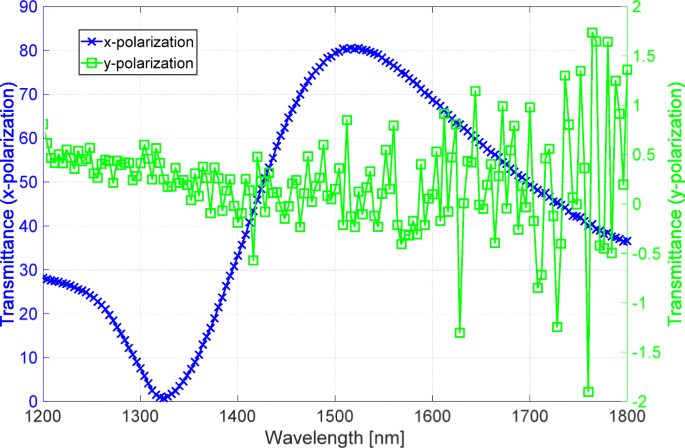
분광광도계로 측정한 투과 스펙트럼. 파란색과 녹색 선은 x의 스펙트럼입니다. 그리고 y 각각의 양극화
그림 5a는 x에 대해 측정된 투과율 스펙트럼을 보여줍니다. 그리고 y 양극화. 높은 투과율에 해당하는 파란색 선은 분광 광도계로 측정한 투과율과 유사한 스펙트럼 프로파일을 가지고 있습니다. 낮은 투과율에 해당하는 녹색 선은 분광 광도계로 측정되지 않은 1625nm의 파장 주변에서 명확한 딥을 가지고 있습니다. x에 대한 투과율을 나눔으로써 y에 대한 양극화 편광, 우리는 그림 5b에 표시된 흡광비 스펙트럼을 평가했습니다. 소광비 스펙트럼은 파장 1640nm 부근에서 20,000을 초과하는 피크값을 갖는다.
<그림>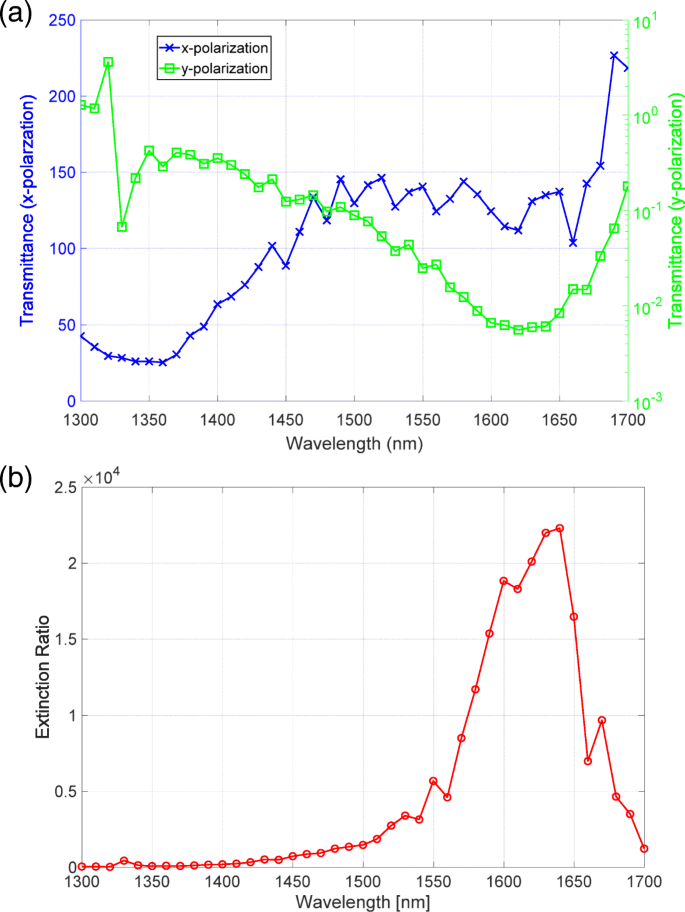
아 x의 투과 스펙트럼 (파란색) 및 y (녹색) 그림 1에 표시된 설정에 의해 측정된 편광. b 메타표면 편광자의 소광비 스펙트럼
측정된 데이터의 유효성을 고려하기 위해 측정된 스펙트럼을 수치 계산 결과와 비교했습니다. 도 6a에 도시된 바와 같이, 높은 투과율 스펙트럼은 분광광도계에 의해 측정된 스펙트럼과 일치하였다. 대수 눈금으로 표시되는 낮은 투과율 스펙트럼은 1640nm의 파장 주변에서 뚜렷한 하강을 나타냅니다. 이 특성은 관찰된 스펙트럼의 특성과 잘 일치했습니다. 도 6b에 도시된 소광비 스펙트럼은 15,000의 피크를 가지며 이는 관찰된 값에 가깝다. 따라서 측정된 투과율 및 소광비 스펙트럼은 수치 계산 결과와 일치하여 20,000을 초과하는 높은 소광비를 성공적으로 관찰했음을 나타냅니다.
<그림>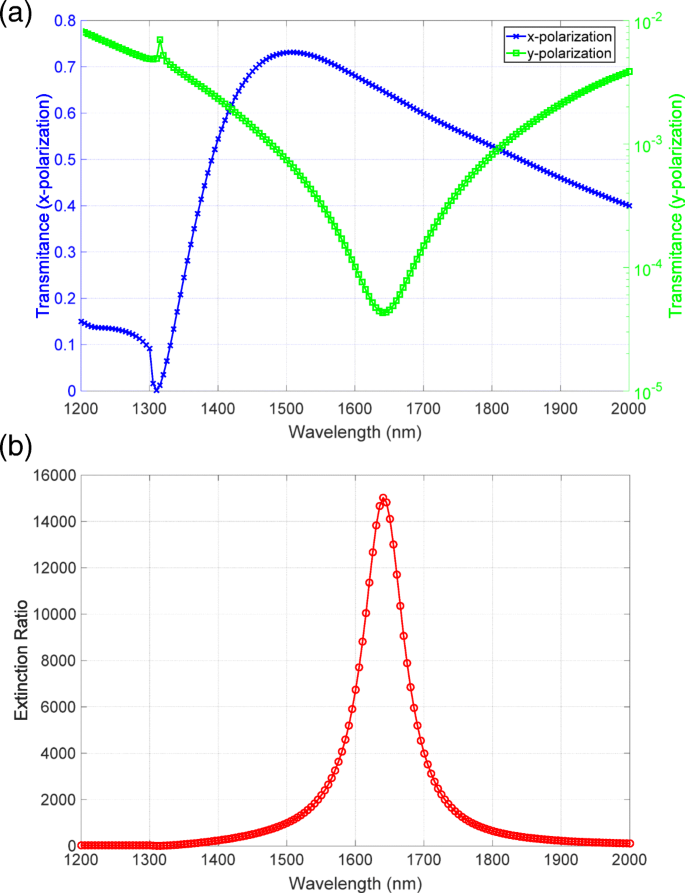
a의 수치 계산 결과 투과율 및 b 소광비 스펙트럼. a의 파란색 및 녹색 선 x에 해당 그리고 y 각각의 양극화
높은 소광비를 갖는 메타표면의 실험적 시연에 이어, 메타표면이 대기에서 분해될 수 있는 Ag를 포함하기 때문에 시간 열화에 대한 안정성에 초점을 맞춥니다. 그림 7은 소광비의 시간 열화를 보여줍니다. 빨간색, 녹색 및 파란색 선은 각각 금속 증착 후 6일, 7일 및 9일 후에 관찰된 소광비 스펙트럼입니다. 빨간색 선은 20,000을 초과하는 피크 값을 가지고 있습니다. 레드 라인 측정 하루 만에 소광율이 떨어졌지만 여전히 피크 값이 10,000을 초과했습니다. 그러나 녹색선 측정 2일 후 소광비는 크게 저하되어 피크값이 500이었다. 청색선은 선폭이 넓어져 손실 증가가 이러한 열화에 수반됨을 알 수 있다. 따라서, 소광비는 급격한 저하를 나타내었고 성능은 한 자릿수 저하되었습니다. 우리는 또한 분해 후 소광비 스펙트럼의 청색 이동 피크를 발견했습니다. 성능 저하와 관련된 중요한 요소에 대한 연구가 설명되어 있습니다.
<그림>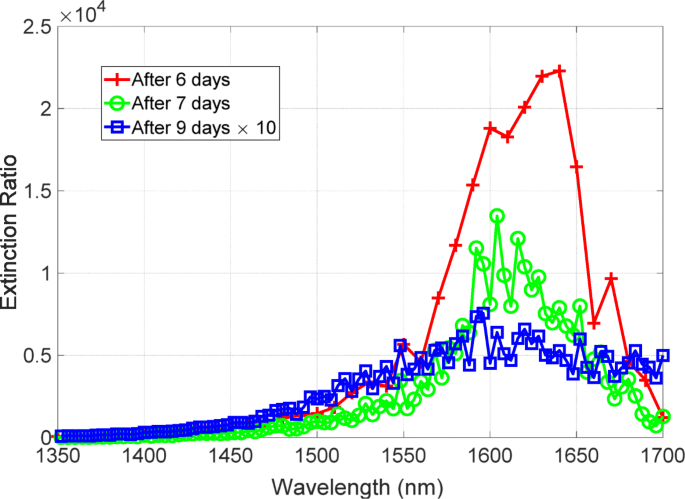
소광비의 시간 저하. 빨간색, 녹색, 파란색 선은 금속 증착 후 6, 7, 9일 동안의 소광비 스펙트럼입니다.
분해는 빠르게 진행되었고 소광 스펙트럼의 선 폭은 넓어졌으며, 이는 일부 구조적 변화가 이 분해 과정에 포함될 것임을 나타냅니다. 따라서 우리는 금속 나노구조의 표면 형태가 편광판의 성능에 영향을 미치는 방식을 조사했습니다. 형태를 설명하기 위해 두 가지 모델을 소개합니다. 하나는 가우스 백색 잡음이 있는 주기적인 곡선으로 표면을 설명하고 다른 하나는 무작위로 분포된 나노 입자로 설명합니다.
먼저 주기 곡선을 사용하여 모델을 조사합니다. 그림 8a는 모델링된 표면을 보여줍니다. CPU 시간과 메모리 리소스를 절약하기 위해 하단 금속 레이어에만 거칠기를 도입했습니다. 거친 표면으로 인해 금속층의 유효 두께가 달라집니다. 따라서 우리는 그림 8b에서 녹색 화살표로 표시된 바닥층의 두께를 변경했습니다. 그림 9a, b는 각각 이 구조의 투과율 및 소광비 스펙트럼을 보여줍니다. 거칠기가 있는 경우에도 메타표면 편광자는 10,000 정도의 높은 소광비를 가지므로 거칠기가 성능을 크게 저하시키지 않음을 나타냅니다. 수치 계산은 또한 두께가 감소함에 따라 소광비의 적색 편이 스펙트럼을 보여주었습니다. 이 적색 편이는 그림 9a에 표시된 투과율의 스펙트럼 특성에 의해 설명됩니다. 높은 투과율은 금속 두께의 변화와 관련하여 매우 낮은 감도를 가지며, 낮은 투과율은 두께가 감소함에 따라 red-shifted dip 위치를 갖는다. 소광비의 피크 위치는 낮은 투과율의 딥에 따라 달라지며 결과적으로 적색 편이가 발생합니다. 계산에서 나타난 적색편이는 실험적으로 관찰된 청색편이의 특징과 일치하지 않는다.
<그림>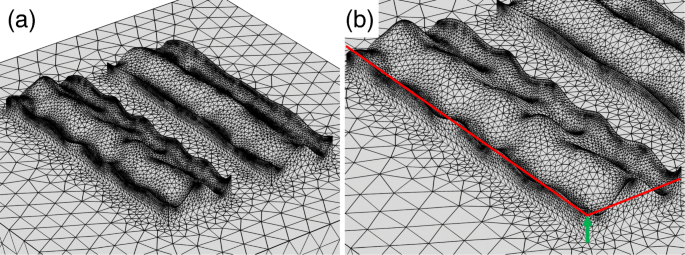
아 가우스 백색 잡음이 있는 주기적 곡선을 사용하여 모델링된 거친 표면. ㄴ 녹색 화살표로 표시된 기본 두께는 계산에서 다양합니다.
<그림>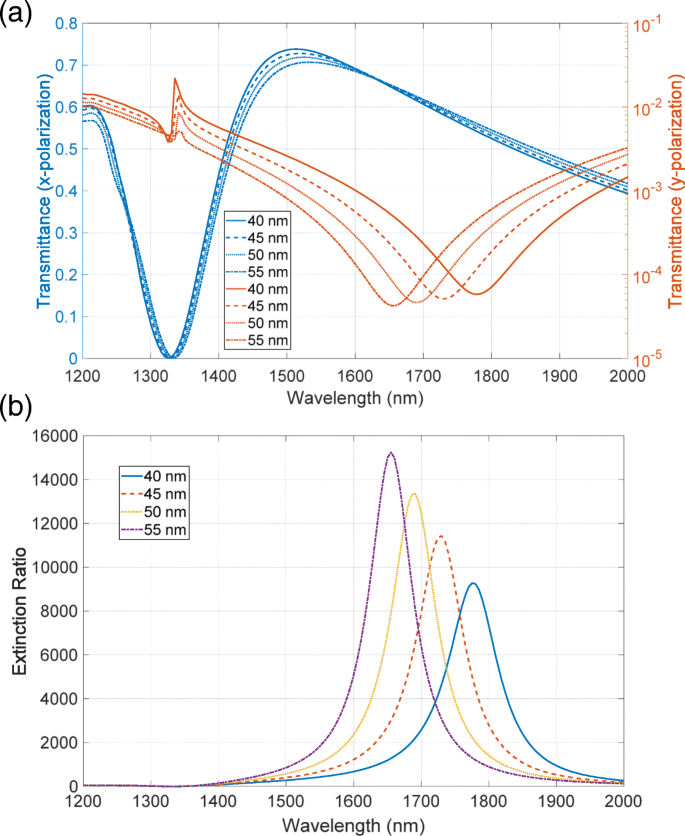
아 투과율 및 b 첫 번째 모델의 소광비 스펙트럼은 그림 8에 나와 있습니다. 바닥 금속층의 기본 두께는 40에서 55nm까지 5nm 간격으로 다양합니다.
둘째, 나노 입자에 의한 모델을 조사합니다. 그림 10a는 15, 20, 25nm 반경의 나노 입자가 그림 10b와 같이 바닥 금속 구조의 표면에 무작위로 분포된 모델링된 표면을 보여줍니다. 우리는 균일하게 분포된 난수에 따라 표면에 반구 모양의 나노 입자를 배치했습니다. 무작위 분포에서 일부 입자는 약간의 공간적 겹침이 있고 입자 사이의 메쉬 크기는 메모리를 극도로 소모하게 됩니다. 이 경우 메모리를 절약하기 위해 입자 중 하나를 수동으로 이동하고 메쉬 크기를 줄였습니다. 바닥 구조의 두께를 40nm로 설정했습니다. 그림 11a, b는 각각 이 구조의 투과율 및 소광비 스펙트럼을 보여줍니다. 첫 번째 모델과 유사하게 소광비 스펙트럼은 10,000 정도의 피크 값을 가지며 크게 저하되지 않습니다. 적색편이 피크는 나노입자의 존재하에서도 나타났다. 이러한 특징 역시 첫 번째 모델에서 관찰된 것과 동일하지만 열화 특성 및 청색편이의 실험 결과와 일치하지 않는다.
<그림>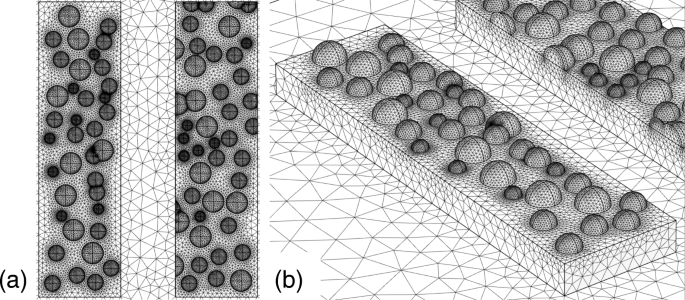
아 평면도 및 b 무작위로 분포된 나노 입자를 사용하여 모델링된 거친 표면의 조감도
<그림>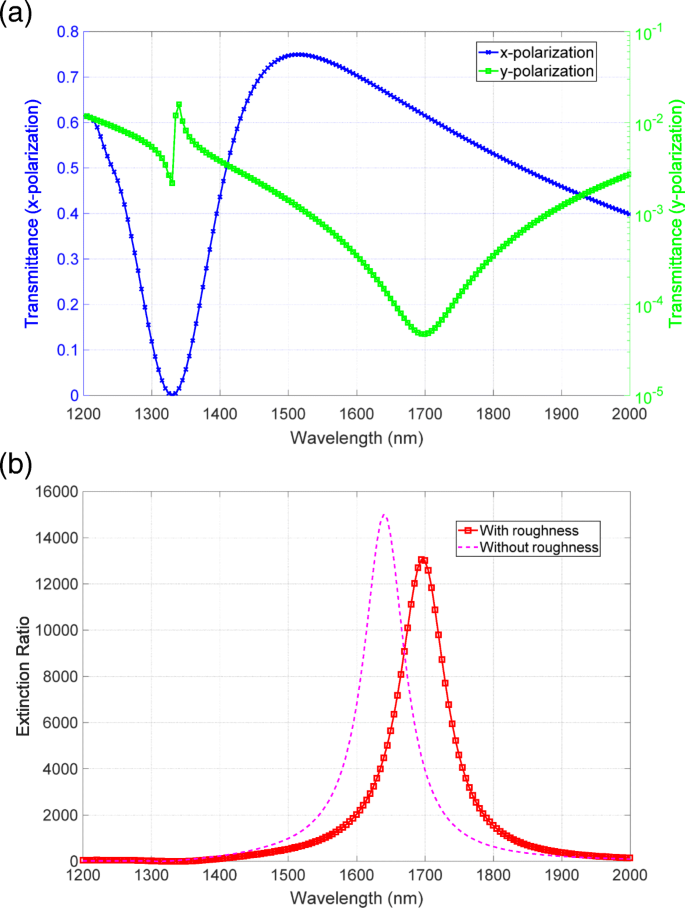
아 투과율 및 b 그림 10에 표시된 두 번째 모델의 소광 스펙트럼
이 단계에서 우리는 표면 형태의 변화가 메타표면 편광판의 성능을 크게 저하시키지 않는다는 것을 수치적으로 보여주었습니다. 이러한 형태의 견고함은 Babinet의 원리에 기인합니다. Babinet의 원리는 표면 형태를 말하는 것이 아니라 보완적인 구조의 스크린을 의미합니다. 이 원리에 기반한 고성능 편광판은 표면 거칠기가 존재하더라도 화면이 불변하여 형태에 대한 강건함을 가져오기 때문에 형태에 크게 영향을 받지 않습니다. 따라서 열화의 원인으로 표면 형태의 또 다른 영향을 고려할 필요가 있습니다. 여기에서는 형태와 관련된 금속 손실에 중점을 둡니다. 표면 거칠기가 증가함에 따라 표면 산란 및 결정립계 효과로 인해 Ag의 허수부가 증가한다[36, 37]. 이러한 손실 증가는 γ로 설명되는 Drude 모델의 감쇠 상수로 설명됩니다. =ρ n 이 2 /나 e , 여기서 ρ , n , e , 및 m e 는 각각 전기 저항률, 전자 밀도, 전자 전하 및 유효 전자 질량입니다. 저항은 두 가지 용어로 구성됩니다. 하나는 벌크 저항이고 다른 하나는 표면 저항입니다. 표면 저항 ρ s 측면 상관 길이 ξ에 반비례합니다. 즉, ρ s ∝ξ −1 [38]. 거칠기가 증가함에 따라 측면 상관 길이 ξ 감소하여 표면 저항과 금속 손실이 높아집니다. 주기 경계 조건이 사용되었고 거친 주기 구조를 가정했기 때문에 이 물리적 메커니즘은 계산에 포함되지 않았습니다. 소광비에 대한 이러한 금속 손실 증가의 영향을 고려하고 Ag의 유전율을 다음과 같이 수정합니다.
$$\begin{array}{@{}rcl@{}} \tilde{\epsilon}_{\text{Ag}} =\text{Re}\left(\epsilon_{\text{Ag}} \right ) + C\times \text{Im}\left(\epsilon_{\text{Ag}}\right)\mathrm{i}, \end{array} $$ (3)여기서 ε Ag 는 [32], C에서 얻은 Ag의 유전율입니다. 는 금속 손실의 증가를 나타내는 상수이고, i는 허수 단위를 나타냅니다. 실수 부분과 허수 부분이 Kramers-Kronig 관계에 의해 연결되기 때문에 허수 부분의 증가에 따라 유전율의 실수 부분을 수정해야 합니다. 본 연구에서는 허수부만을 수정하여 정성적 논의를 하였다. 이 수정된 유전율을 사용하여 소광비 스펙트럼을 계산합니다. 이 결과는 그림 12에 나와 있으며, 여기서 상수 C 1에서 5까지 다양하다. 소광비는 금속 손실이 증가함에 따라 급격히 감소한다. 또한, 스펙트럼의 피크 위치는 손실이 증가함에 따라 청색 편이 특성을 나타냈다. 급격한 저하와 청색 편이의 이러한 특징은 실험적으로 관찰된 특징과 잘 일치합니다. 이 청색편이의 기원은 다음과 같이 설명된다. 낮은 투과율의 dip 값은 금속 손실이 증가함에 따라 점점 더 얕아집니다. 그 결과, 높은 투과율의 피크값에서 소광비에 대한 기여도가 증가합니다. 피크 위치는 금속 손실에 대한 강한 둔감성을 가지며 딥 위치보다 파장이 더 짧기 때문에 소광 스펙트럼의 청색 편이가 발생합니다. 따라서 우리는 허수부의 증가가 저하의 원인이 되는 결정적인 요인임을 발견했습니다.
<그림>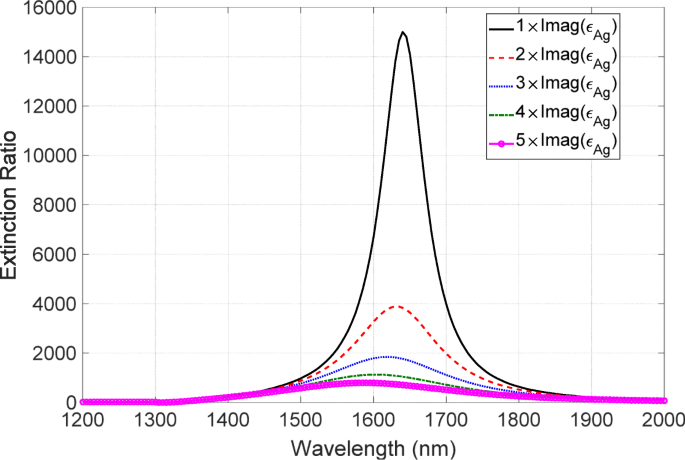
소멸 스펙트럼의 금속 손실 의존성. 검정, 빨강, 파랑, 녹색 및 자홍 선은 C의 경우에 해당합니다. =1,2,3,4 및 5, 각각
우리는 보완 금속 층의 두께를 변화시켜 소광비를 향상시킬 것을 제안합니다. 높은 투과율의 피크 위치는 낮은 투과율의 딥 위치보다 짧은 파장에 위치합니다. 소광비를 높이려면 이러한 피크와 딥 위치가 서로 가까워야 합니다. Babinet의 원리에 따르면 피크와 딥은 동일한 파장에 있어야 합니다. 그러나 원리는 보완 구조가 무한히 얇은 두께의 완벽한 전기 전도체를 구성한다고 가정하며, 이는 근사치에서도 광학 영역에서 검증하기 어렵습니다. 결과적으로 상보적 구조는 서로 다른 공진 파장을 갖습니다. 파장을 조정하기 위해 공진을 담당하는 고유 모드의 특성을 고려합니다. 도 13a, b는 각각 도 6에 도시된 투과율의 피크 및 딥 위치에서의 전기장 및 자기장 분포 패턴을 나타낸다. 이러한 필드 분포는 z -x y에서의 비행기 1 W의 입사광 강도에서 =0. 높은 투과율의 고유 모드는 상부 금속 구조에서 전기 쌍극자의 특성을 갖는 반면, 낮은 투과율의 고유 모드는 하부 구조에서 자기 루프의 특성을 갖는다. 높은 투과율을 위한 공명 파장은 z의 공기 구멍의 너비에 의해 결정됩니다. -x 비행기. 이것은 고정된 매개변수이며 조정할 수 없습니다. 한편, 저투과율에 대한 공진 파장은 z에서 바닥 구조의 단면에 의해 결정됩니다. -x 비행기. 이것은 금속 두께를 변경하여 조정할 수 있습니다. 이러한 조정은 높은 투과율의 피크 위치가 바닥 금속층의 두께에 대해 낮은 감도를 갖는 반면 낮은 투과율의 딥 위치가 높은 감도를 갖는다는 투과율의 두께 의존성과 일치합니다. 이 분석을 바탕으로 파장을 다음과 같이 조정합니다. 두께가 증가함에 따라 단면이 증가하고 낮은 투과율의 공진 파장이 더 짧은 파장으로 이동합니다. 결과적으로 피크 및 딥 위치가 가까워지고 소광비가 향상됩니다. 이를 확인하기 위해 두께에 대한 투과율 및 소광비 스펙트럼의 의존성을 계산합니다. 이 계산에서 우리는 상단 금속층의 두께를 45nm로 고정했습니다. 그림 14a는 x에 대한 투과율 스펙트럼을 보여줍니다. 그리고 y 양극화. 두께가 증가함에 따라 낮은 투과율의 dip 위치는 더 짧은 파장으로 이동하고 dip은 더 깊어진다. 반면, 고투과율의 피크 위치는 피크 값이 ~ 5% 감소하더라도 두께를 변화시켜도 크게 영향을 받지 않는다. 그림 14b는 소광비 스펙트럼을 보여줍니다. 두께가 35nm 또는 40nm일 경우 저투과율의 딥이 45nm보다 얕아져 소광비가 낮아진다. 두께가 50nm 또는 55nm일 때 향상이 거의 없습니다. 이는 피크 및 딥 위치 조정에 의한 향상이 높은 투과율의 피크 값의 감소에 의해 상쇄되기 때문입니다. 두께가 60 또는 65 nm일 때 소광비가 분명히 향상됩니다. 이것은 더 깊은 딥 값과 위치 조정에 의한 향상의 조합 때문입니다. 우리가 수치적으로 나타낸 바와 같이, 소광비의 추가 향상은 상보적인 금속 구조의 두께를 조정함으로써 실현될 수 있다. 이러한 다양한 두께는 금속 증착을 반복하여 실현할 수 있습니다. 먼저 a 두께의 금속 증착 패턴이 있는 기판에서 수행됩니다. 그런 다음 깨끗한 천으로 닦으면 금속 두께가 a인 기판 표면에서 상단 금속층만 제거됩니다. . 그 후, b 두께의 금속 증착 샘플에 대해 수행됩니다. 결과적으로 상단 및 하단 레이어의 두께는 b가 됩니다. 그리고 a +ㄴ , 각각.
<그림>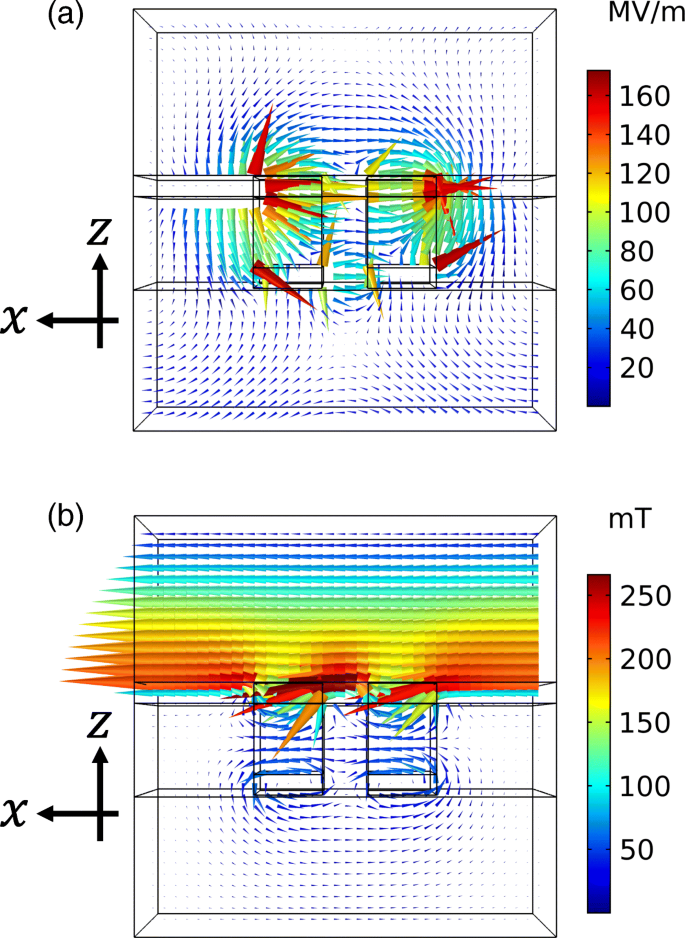
아 고투과율 피크에서의 전계 분포 패턴은 Fig. 6과 같다. b 그림 6과 같이 낮은 투과율의 딥에서의 자기장 분포 패턴. 유사 색상은 벡터 필드의 강도를 나타냅니다.
<그림>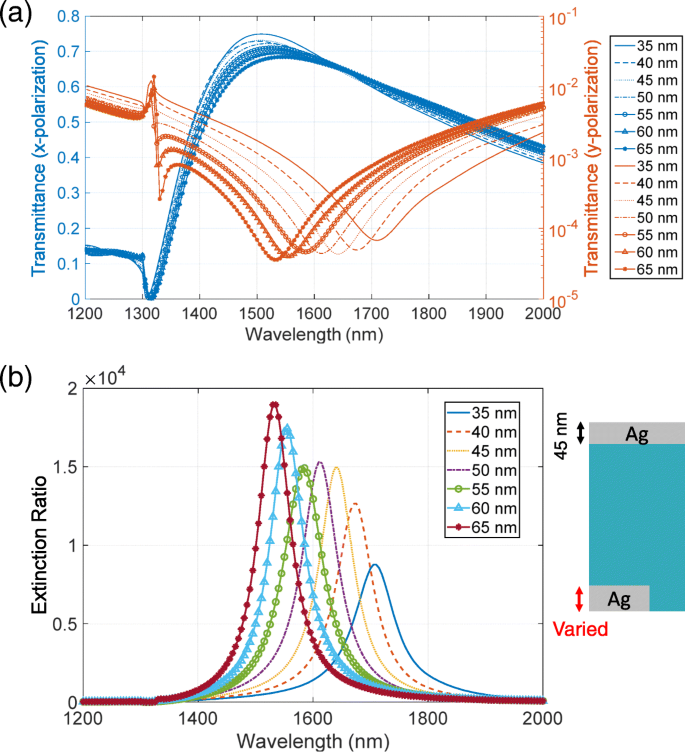
아 투과율 및 b 상보적인 금속 층이 서로 다른 두께를 가질 때의 소광비 스펙트럼. 상단 금속층의 두께는 45nm로 고정되고 하단층의 두께는 5nm 간격으로 35~65nm로 변경됩니다(b의 삽입 참조). )
고성능 메타표면 편광판의 열화 특성을 조사했습니다. 준비된 메타표면은 10,000 정도의 높은 소광비를 보였다. 우리는 고성능이 점차 저하된다는 점에 주목했습니다. 이 분해의 기원을 명확히 하기 위해 우리는 소광비에 대한 표면 형태의 영향을 조사했습니다. 표면 형태를 설명하기 위해 두 가지 모델이 제시되었습니다. 하나는 주기 곡선과 가우시안 백색 잡음의 조합으로 거친 표면을 모델링하는 반면, 다른 하나는 무작위로 분포된 나노 입자로 표면을 모델링합니다. 두 모델 모두 표면 거칠기에 의해 고성능이 저하되지 않는 것으로 나타났습니다. 이는 높은 소광비가 Babinet의 원리에 의해 지배되어 표면 형태가 강건하기 때문입니다. We have also investigated the relation between the extinction ratio and the increase in metallic loss because of the surface roughness, which showed drastic degradation of the extinction ratio. The spectral feature of the blue-shift was also reproduced by the numerical calculation, indicating that the degradation is due to the increase in the metallic loss. From this result, we find that the metal deposition should be conducted to reduce the scattering and grain boundary losses that are related to the roughness. Throughout the numerical calculation, we have found that the low transmittance has a high sensitivity to the surface morphology, while the high transmittance does not have the high sensitivity. By utilizing these findings, we proposed that the extinction ratio can be enhanced by varying the thicknesses of the metallic layers. This study paves a way for the development of a metasurface with a high performance and stability toward time degradation.
Beam sampler
Glan-laser prism
Neural density filter
Optical parametric oscillator
Photonic crystal
주사 전자 현미경
Yttrium iron garnet
나노물질
초록 마찰전기 나노발전기(TENG)의 출력 전력은 마찰전기 물질, 특히 미세구조 및 작용기의 성능에 크게 의존합니다. 이 연구에서는 우수한 마찰 전기 능력을 목표로 층별 적층을 통해 풍부한 플루오르 그룹(-F)을 갖는 교대로 적층된 MXene 복합 필름 기반 TENG를 설계 및 제조합니다. Nb2의 양이 많을 때 균일한 고유 미세구조와 증가된 유전 상수의 이점 CTx 나노시트는 Nb2를 기반으로 하는 TENG가 15wt%로 증가합니다. CTx /Ti3 C2 Tx 복합 나노 시트 필름은 최대 출력을 달성합니다. 8.06μA/c
정밀 가공은 우리가 일상 생활에서 사용하고 의존하는 많은 도구의 부품 및 구성 요소를 만드는 데 사용할 수 있는 기본 서비스입니다. 우리가 서비스하는 모든 산업은 항공 우주, 의료, 자동차 자동화 등을 포함한 고급 가공을 필요로 합니다. 하지만 정밀 가공이란 정확히 무엇입니까? 정밀가공이란 무엇인지, 가공방법과 장점, 고정밀 가공이 왜 중요한지 자세하게 소개합니다. 고정밀 가공이란 무엇입니까? 제조 산업에서 고정밀 가공 는 일반적으로 허용 오차가 몇 마이크로미터 이내인 부품을 나타냅니다. 정밀 가공 공정은 가공 정확도와 표면