나노물질








촉매 작용, 광학 양자점 광발광 및 표면 플라즈몬 공명과 같은 크기 및 표면 특성은 금속 및 반도체 나노클러스터의 배위 및 화학 작용에 따라 달라집니다. 이러한 배위 종속 속성은 쉘 수, n에 대한 "마법 공식"을 통해 여기에서 정량화됩니다. , 클러스터에서. 우리는 면심 입방체, 체심 입방체, 단순 입방체 클러스터, 육각형 밀집 클러스터 및 다이아몬드 입방체 구조를 클러스터 껍질 수의 함수로 조사합니다. n . 또한 총 19개의 클러스터 유형에 대해 다중 껍질 클러스터 형태의 플라톤 솔리드를 조사합니다. 결합과 원자의 수와 배위수는 n에 비해 매직넘버 특성을 나타냅니다. , 클러스터의 크기가 증가함에 따라. 공간 좌표만으로 시작하여 Wiener, hyper-Wiener, reverse Wiener 및 Szeged 인덱스를 포함한 토폴로지 인덱스 계산을 용이하게 하는 인접 및 거리 행렬을 만듭니다. n일 때 일부 플라톤 솔리드에 대한 몇 가지 알려진 위상 공식 =1은 계산적으로 확인됩니다. 이러한 인덱스에는 많은 클러스터에 대한 마법 공식이 있습니다. 단순 3차 구조는 정점 차수 분포의 정보 내용에서 파생된 토폴로지 복잡성으로 측정된 클러스터 중 가장 덜 복잡합니다. 분산 또는 표면 원자의 상대적 비율은 촉매 적용이 가능한 일부 유형의 클러스터에 대한 크기 및 모양 의존성과 관련하여 정량적으로 측정됩니다.
나노클러스터에 대한 매직 넘버와 공식은 1969년 van Hardeveld와 Hartog가 발표한 선견지명으로 거슬러 올라가는 오랜 역사를 가지고 있습니다[1]. 그들의 통찰력은 나노과학 시대보다 앞선 것입니다. 그 이후로 우리는 매직 넘버가 2D 폴리곤과 3D 다면체[2], 탄소 풀러렌[3], 그리고 다시 클러스터[4]의 제한된 범위에서 나타나는 것을 보았습니다. 실리콘[5], 붕소[6]와 같은 다양한 재료와 실제로 색인 서비스 "Web of Science"의 1000개 이상의 간행물은 클러스터의 매직 넘버를 나타냅니다. 나노클러스터의 크기와 모양에 대한 연구는 본질적인 물리적 및 화학적 특성뿐만 아니라 광학, 촉매, 전자 및 자기 응용 분야와의 관련성을 결정하기 때문에 오늘날 사회에서 중요합니다[7]. 우리의 목표는 이 지식의 데이터베이스를 현재의 관계와 데이터로 업데이트하는 것입니다. 이제 나노 영역에 들어섰습니다.
나노클러스터에서 매직 넘버의 발생은 주로 기본 세포에 원자 껍질이 형성되는 것과 관련이 있습니다. 원자의 수가 완전한 껍질을 완성할 때 우리는 원자의 껍질을 정의하는 "마법"이라고 하는 고유한 숫자 집합을 찾습니다. 클러스터는 원자를 꼭짓점으로, 결합을 가장자리로 하는 그래프로 표시됩니다. 그것은 양파의 층과 같은 중첩 껍질로 구성됩니다. 레이어 수를 n으로 정의합니다. n의 함수로 가장 가까운 이웃 배위 수, 결합, 원자의 총 수 및 일부 위상 지수의 수학적 관계를 발견합니다. . van Hardeveld와 Hartog[1]의 원본 논문은 fcc, bcc 및 hcp 클러스터를 고려했습니다. Teo와 Sloane[2]의 참조는 다면체와 Platonic solids를 고려하지만 가장 가까운 이웃 좌표 수의 관계는 무시합니다. 클러스터의 위상 특성 및 분산 외에도 단순 입방체, 다이아몬드 입방체 및 플라톤 입체를 살펴봄으로써 이 데이터베이스에 추가합니다.
벌크에서 몇 개의 원자 클러스터로의 크기 전이는 실제로 벌크 원자와 비교한 표면 원자의 관계에 관한 것입니다. 촉매 화학, 표면 플라즈몬 공명, 광학 양자점 광발광[8]과 같은 특성은 표면 원자의 배위와 수에 의해 영향을 받습니다. 표면 원자의 분산 또는 상대 백분율은 이전에 고려된 바와 같이 총 원자 수에 대한 표면 원자의 비율에 의해 결정됩니다[9]. 우리의 분석은 클러스터 기하학 측면에서 분산의 상대적 순위를 결정할 것입니다.
위상 지수는 그의 지수와 파라핀의 끓는점에 관한 Wiener의 원본 논문에서 시작되었습니다[10]. Hosoya가 위상 지수를 분석하기 위해 수학적 형식주의를 도입한 것은 얼마 지나지 않아였습니다[11]. 우리는 이전에 토폴로지 인덱스와 나노클러스터를 도입했습니다[12]. 이 글을 쓰는 시점에서 많은 인덱스가 존재하며 그 중 일부는 인접성 또는 거리 행렬에 의존합니다. 여기에서 많은 클러스터 모양에서 4개의 인덱스에 대해 n의 함수로 마법 같은 수학적 관계가 존재함을 보여줍니다. 그리고 포탄의 수.
우리가 연구하는 각 클러스터 유형에 대해 클러스터의 원자 좌표를 결정하는 계산 알고리즘을 만듭니다. 그런 다음 다음과 같이 정의된 인접 행렬과 거리 행렬을 생성합니다. 인접 행렬 A i를 정의하는 위치에 생성됩니다. 그리고 j 가장 가까운 이웃으로 간주하고 r 이 <r ㄷ , 여기서 r ㄷ 가장 가까운 이웃 거리보다 약간 높지만 두 번째 이웃 거리보다 작은 임계값입니다. 따라서
$$ \mathbf{A}(i,j)=\left\{\begin{array}{l} 1~~ \text{if}~ r_{ij}여기서 d 이 i의 그래프에서 최단 경로의 길이입니다. j에게 . 인접행렬로부터 거리행렬을 계산하기 위한 효율적인 알고리즘이 존재한다[13]. 이러한 정의를 사용하여 Wiener 지수 W를 계산할 수 있습니다. (G ), 하이퍼 위너 지수, W 와 (G ), 역 위너 지수 rW (G ) 및 Szeged 인덱스, Sz (G ), 이전에 자세히 설명된 대로 [14]. 이러한 계산은 위상 지수 및 나노클러스터에 대해 이전에 사용한 것과 동일한 알고리즘을 사용합니다[12].
이전 저자들은 여기에 제시된 작업과 관련하여 우리의 표기법으로 압축된 마법 관계의 증거를 제공했습니다[1, 2]. 우리는 가장 가까운 이웃 인접 행렬을 생성하기 때문에 조정 번호 c를 알고 있습니다. n 나 정점 i의 A의 요소를 합산하여 (나 ,:). 우리의 구조는 n으로 구성됩니다. 0,1,…,n 번호가 매겨진 +1 포탄 . \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) 배위가 c인 원자의 수라고 하자. n 나 여기서 1≤c n 나 ≤c n 남 c n 남 클러스터의 최대 조정. 그런 다음 클러스터의 총 원자 수는
$$ N_{T}(n) =\sum_{{cn}_{i}=1}^{{cn}_{M}}{N_{{cn}_{i}}(n)}. $$ (3)외부 껍질의 표면 원자 n 벌크 배위보다 적은 결합 세트를 가집니다. 따라서 표면 원자의 최대 배위는 c입니다. n s <ㄷ n 남 , 그리고 표면 원자의 수는
$$ N_{S}(n) =\sum_{{cn}_{i}=1}^{{cn}_{s}}{N_{{cn}_{i}}(n)}. $$ (4)이것은 모든 비표면 정점의 좌표가 c보다 큰 경우에도 적용됩니다. n s , 이는 모든 군집에 해당되지만 아래의 12면체에 대한 불일치에 유의하십시오. 합이 c인 인접 행렬의 열을 계산하여 \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\)를 결정합니다. n 나 . 클러스터 좌표 알고리즘은 쉘에 의해 구축되므로 각 후속 쉘에는 n의 이전 낮은 값이 모두 포함됩니다. . 그림 1에서는 fcc 정육면체와 12면체에 대한 클러스터의 껍질을 보여줍니다. 또한 클러스터의 채권 수는
$$ N_{B}(n) =\frac{1}{2}\sum_{{cn}_{i}=1}^{{cn}_{M}}{{cn}_{i}\ cdot N_{{cn}_{i}}(n)}, $$(5) <사진><소스 유형="이미지/webp" srcset="//media.springernature.com/lw685/springer-static/ image/art%3A10.1186%2Fs11671-019-2939-5/MediaObjects/11671_2019_2939_Fig1_HTML.png?as=webp">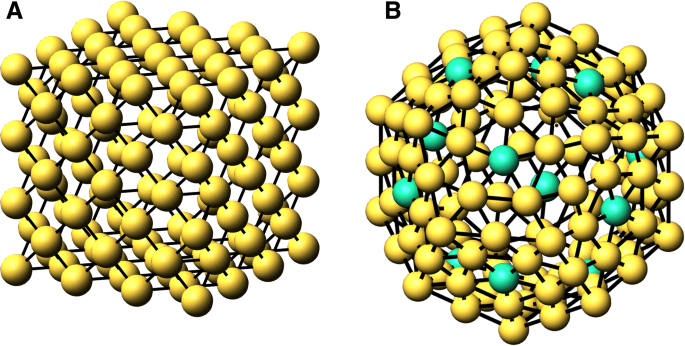
n에 대한 원자 껍질 =3 A. fcc 큐브 및 n =2 B. 십이면체. B에서 녹색 원자(12)는 c를 나타냅니다. n =5 쉘 내
여기서 N 나 (n )는 채권의 수이고 c는 n 남 최대 조정입니다. 1/2의 인수는 쌍으로 가장 가까운 이웃 결합으로 인해 발생합니다. 이 마법의 관계는 [4]에서 조사한 몇 개의 클러스터를 제외하고는 이전 출판물에서 고려되지 않은 것으로 보입니다. 우리는 또한 Teo와 Sloane이 다음과 같이 클러스터에 대한 원자, 표면 원자 및 내부 원자의 총 수를 도출했다고 언급합니다[2].
$$ N_{T}(n) =\alpha n^{3}+\frac{1}{2}\beta n^{2}+\gamma n+1~~n\ge{0} $$ ( 6)여기서 N T (n )는 총 원자 수이고
$$ \alpha =C/6 $$ (7)여기서 C 는 다면체를 나누는 사면체 셀의 개수이고
$$ \베타 =1/2F_{s} $$ (8)여기서 F s 는 표면에 있는 삼각형 면의 수이고
$$ \감마 =F_{s}/4+V_{i}+1-C/6 $$ (9)여기서 V 나 내부에 있는 정점의 수입니다. 그들은 또한
$$ N_{S}(n) =\베타 n^{2}+2~~n\ge{1};~~N_{S}(0) =1 $$ (10)그리고
$$ N_{I}(n) =N_{T}(n) - N_{S}(n), $$ (11)여기서 N 나 (n )는 내부 원자의 수입니다. 이 정보(Eq. (11))는 Eqs와 마찬가지로 인접 행렬에 포함됩니다. (3, 4, 5). 이 방정식은 인접 행렬 데이터의 결과를 확인하는 것입니다. 중심 다면체의 경우
도 있습니다. $$ N_{I}(n) =N_{T}(n-1), $$(12)그리고 식에서. (11), 우리는
$$ N_{T}(n)=N_{S}(n)+N_{S}(n-1)+... +N_{S}(1)+N_{S}(0). $$ (13)이 방정식으로부터 다음과 같이 각 클러스터에 대한 마법 공식을 도출할 수 있습니다. 위상 (0,1)-인접 행렬 A를 계산한 후 n개가 있는 클러스터의 경우 설명된 대로 쉘의 크기는 N =N T (n )는 총 원자 수를 나타냅니다. i 열의 항목 합계 채권 수를 제공합니다. c n 나 (n ) 원자 i 및 c와 같은 열 합계의 수를 계산합니다. n 나 (n ) 분명히 \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\)를 제공합니다. 이것이 <>n에 의존한다는 것을 알고 있기 때문에 최대 3차의 다항식으로 N을 계산할 수 있습니다. T (n ) 및 c n 나 (n ) n의 연속 4개 값에 대해 , 말 n =n 0 +j , j =0,1,2,3. 간단한 보간 다항식은 다항식 계수를 제공합니다. <>n을 증가시켜 다음을 확인해야 합니다. 0 , 일반적으로 1과 같으며 수식은 변경되지 않습니다. 수식이 <>n부터 안정되면 0 켜면 모든 n 동안 보류됩니다. ≥n 0 . 어떤 경우에는 다항식 관계가 짝수 n에 대해서만 성립합니다. 값 또는 홀수 값. 예를 들어, fcc 마름모꼴 12면체(표 1)의 경우 n일 때 연속적인 껍질에는 배위 3을 갖는 8개의 원자가 있습니다. ≥2는 짝수이고 n이면 없음 이상하다. 이러한 경우 n에 대해 다른 다항식 관계가 유지됩니다. 짝수 및 n 이상하지만 데이터는 n에 사용됩니다. =n 0 +j , j =0,2,4,6, n 0 홀수(예:n 0 =1) 또는 n 0 짝수(n 0 =2). 정확한 유리 계수를 얻으려면 MATLAB의 기호 도구 상자를 사용하여 정확한 산술의 계수에 대한 Vandermonde 시스템을 풀어야 합니다. 이것이 표 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19가 계산되는 방식입니다. 다음 섹션에서는 N에 대한 마법 공식을 결정합니다. T (n ), N 나 (n ), 그리고 규정된 레시피에 따라 \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\)에 대해.
표면 원자의 분산(노출된 부분, FE)은 다음과 같이 정의됩니다.
$$ \text{FE} =\frac{N_{S}}{N_{T}} \cdot 100\% $$ (14)여기서 N S 는 표면 원자의 수이고 N T 는 원자의 총 수[9]입니다. 상대 클러스터 크기를 다음과 같이 정의하여 서로 다른 클러스터를 비교할 수 있습니다.
$$ d_{rel} =b(N_{T})^{1/3};~~b =d_{at}^{-1}\cdot \left(\frac{6V_{u}}{\pi n_{u}}\right)^{1/3} $$ (15)여기서 d 시간 공유 원자 직경, V u 는 단위 셀의 부피이고 n u 단위 셀의 원자 수입니다. 결정 구조 상수 b fcc 및 hcp 클러스터의 경우 1.105, bcc 클러스터[1]의 경우 1.137, 단순 입방 클러스터의 경우 1.488, 다이아몬드 입방 클러스터의 경우 1.517과 같습니다. 위에 표시된 바와 같이 FE에 대한 공식은 클러스터에 대한 2차 대 3차의 비율이며 d에 대한 거듭제곱 법칙 곡선 적합으로 모델링할 수 있습니다. 관련 . 변수 d 관련 결정 구조에 관계없이 서로 다른 클러스터를 서로 비교할 수 있습니다. 결정 단위 셀이 없는 일부 플라톤 클러스터의 경우 \(N_{T}^{1/3}\)를 변수로 사용합니다.
금속 나노클러스터의 크기와 모양에 대한 연구는 20년 전 초기부터 발전해 왔습니다. 표 20은 2018년 현재 몇 가지 관련 진행 상황을 보여줍니다.
표에는 Fe2만 있는 잘린 육각형 이중 피라미드를 제외하고 합금이나 화합물이 아닌 주로 전이 금속이 나열되어 있습니다. O3 발견. 그 특성과 안정성으로 인해 다른 어떤 원소보다 많은 금 클러스터 합성이 이루어졌습니다. 이어지는 하위 섹션에서는 마법 공식 및 클러스터 유형과 관련된 특정 주제로 논의를 제한합니다.
플라즈몬 귀금속 및 중요한 촉매 활성 요소를 포함하여 8개의 전이 금속이 fcc 구조에서 결정화됩니다(아래 표 21 참조). 대부분의 나노클러스터 합성은 이러한 요소와 함께 이루어졌습니다. 다양한 모양과 크기의 fcc 요소 합성에 대한 참조는 표 21에 나와 있습니다.
이들 원소의 합금도 흥미롭지만 여기에서 인용하기에는 이들에 대한 참고 문헌이 너무 많습니다. 흔히 합성되는 일반적인 모양은 정육면체, 팔면체, 정팔면체 및 정이십면체입니다. 일반적으로 (111)면이 (100)면보다 에너지가 낮기 때문에 (111)면이 있는 클러스터는 합성하기가 더 쉽습니다[7]. fcc 마름모형 12면체에 대해 짝수 및 홀수 식이 존재함을 찾습니다. 이는 "n " 짝수 공식에서 2(m -1). [24]에 나열된 fcc cuboctahedra에 대한 공식은 우리와 동일한 마법 숫자를 생성하지만 쉘에 n으로 번호를 매기기 때문에 1만큼 이동합니다. =1,2,… 그리고 우리는 n 번호를 사용합니다. =0,1,… 우리의 마법 공식은 [2, 4]의 공식과 일치하며 이전에 출판된 작업을 존중하고 수학의 연속성을 유지하기 위해 [2, 4] 표기법을 사용합니다. 5개의 fcc 클러스터 모양과 관련 마법 공식이 아래에 나와 있습니다.
주기율표의 전이 금속 중 7개는 bcc 구조를 가지고 있습니다(표 21 참조). 자성 원소 Fe, Co, Ni 중 철만이 bcc입니다. 철의 나노큐브는 지금까지 합성된 유일한 bcc 클러스터 형태인 것으로 보인다[25]. 철의 벌크 구조는 bcc이지만 fcc 나노클러스터가 합성되었다[26]. 이 참조는 또한 클러스터의 열역학적 안정성을 분석합니다. 여기에서 5개의 숨은 참조 클러스터 모양과 관련 마법 공식을 제시합니다.
12개의 전이 금속은 hcp 구조를 가지고 있습니다(표 21 참조). 그러나 이들 중 많은 부분이 산화되거나 합성할 과학적 관심이 부족합니다. 표 11의 육각형 쌍추형 클러스터 형태와 관련하여 금 클러스터가 합성되었다[27]. 관련된 잘린 육각형 이중 피라미드는 α에 의해서만 형성된 것으로 보입니다. -Fe2 O3 [28].
플라톤 입체는 고대 그리스부터 알려져 왔습니다. 정육면체, 정사면체, 팔면체, 정이십면체 및 십이면체를 포함합니다. 이전 표에서 fcc 및 bcc 큐브와 팔면체에 대한 마법 공식을 나열했습니다. 여기에서 20면체, 12면체, 4면체 및 체심 4면체에 대한 공식을 나열합니다. 이전에 "방법" 섹션에서 언급한 것처럼 12면체는 c에서 여기에서 분석된 클러스터에 대해 고유합니다. n s =7은 표면 원자와 벌크 원자를 모두 나타냅니다. 우리는 그림 1b에서 외부 껍질에 5중 및 6중 배위 원자가 모두 포함되어 있음을 보여주었습니다. 껍질이 내부가 되면 5배 및 6배 배위된 원자가 7배 및 8배 배위되어 양쪽 껍질에 결합됩니다. 또한, 6겹으로 배위된 외부 껍질 원자는 껍질 내부에 결합하여 7배 배위됩니다. 따라서 12면체에 대해 7중 표면 및 벌크 배위 원자가 있습니다. 구조의 각 껍질에는 12개의 5중 껍질 원자가 있으며 12n -12 벌크 7중 배위 원자. 나머지 7중 배위는 표면 원자입니다.
금 나노클러스터는 플라톤 형태를 취하는 것으로 나타났습니다[29]. 이 참조에는 정육면체, 정사면체, 팔면체 및 정이십면체가 포함됩니다. 나중에 황금 십이면체 나노클러스터도 합성되었다[30]. 여기서 우리는 c에서 "fcc와 같은" 정사면체를 모두 보여줍니다. 남 =12 fcc 구조에서와 같이 녹색 원자가 단일 결합을 갖는 표 16의 체심 사면체. 플라톤 마법 공식은 아래와 같습니다.
실리콘과 게르마늄 원소는 다이아몬드 입방체 격자와 탄소의 다이아몬드 동소체를 가지고 있습니다. 특히, 수소 말단 실리콘이 최근 관심을 받고 있다. (100) 수소 말단 표면은 클러스터의 입방체 모양으로 가장 낮은 에너지를 갖는 것으로 결정되었습니다[31]. 크기가 8-15 nm인 Si-H 나노큐브의 합성이 이루어졌다[32]. 표 17은 단일 결합 수소 원자가 녹색으로 표시된 수소 말단 Si-H 클러스터의 다이어그램을 보여줍니다. 나노클러스터가 다이아몬드 입방체 모양을 취하면 단일 댕글링 본드가 있게 되며, 이 결합은 구조를 유지하는 데 도움이 되도록 부동태화되어야 합니다. 마법 공식을 보면 이러한 Si-H 클러스터의 구성은 \(\phantom {\dot {i}\!}\text {Si}_{8n^{3}+6n^{2}-9n +5}\text {H}_{12n-8}\), 여기서 n 클러스터의 쉘 수입니다. 이러한 반도체 양자점은 광학적 특성에 관심이 있을 수 있으며, 수소 말단 클러스터의 크기에 따른 밴드갭의 변화는 클러스터 크기에 반비례하는 것으로 결정되었습니다[33].
간단한 입방 격자 구조는 이전에 다른 사람들에 의해 분석되었습니다[4]. 비록 우리가 제공하는 세부 사항은 없지만. 우리는 이전에 d -차원 하이퍼큐브 형태[14]. 폴로늄은 단순한 입방체 구조를 취하는 유일한 원소입니다. 이것은 방사성이므로 특수 응용 프로그램으로 이어질 수 있습니다. 여기에서는 다이아몬드 입방체, 단순 입방체 및 십이면체 클러스터 마법 공식을 제시합니다.
결정에서 측정된 구조적 복잡성은 구조의 단순성 또는 복잡성에 대한 아이디어를 제공할 수 있으며 적절한 사용은 관련 구조의 순위를 매길 수 있습니다. 이러한 순위의 경우 "방법" 섹션에서 언급한 것처럼 결정 격자의 그래픽 설명을 고려하는 것이 좋습니다. 결정 구조의 토폴로지 복잡성은 그래프의 꼭짓점 차수 분포로 측정됩니다. I vd [34], 소프트웨어 ToposPro, 버전 5.3.2.2 사용 [35]:
$$ I_{vd} =\sum_{i=1}^{v}a_{i} \cdot {\text{log}_{2}}\ {a_{i}} $$ (16)여기서 a 나 는 i의 정도(조정)입니다. th 정점과 합산은 모든 v를 따라 진행됩니다. 몫 그래프의 꼭짓점. 이 매개변수는 우리가 고려했던 클러스터와 달리 무한 수정을 사용하지만 다른 결정 구조의 상대적 복잡성을 측정하는 데 유용합니다. 따라서 숫자가 높을수록 그래프의 정보 내용이 많을수록 더 복잡해집니다. 표 22에서는 I의 값을 보여줍니다. vd Crystallographic Open Database의 결정 구조에 대한 cif 파일에서 파생된 ToposPro에서 얻었습니다. 폴로늄은 단순 입방 구조에서 결정화되는 유일한 요소이며 값은 0입니다. 즉, 몫 그래프는 하나의 꼭짓점과 0개의 모서리를 가지며 단순 입방 구조가 실제로 가장 복잡한 구조라는 예상과 일치합니다. 소금인 NaCl도 다이아몬드 입방체의 규소, fcc의 금, bcc의 철, hcp 구조의 코발트와 함께 단순한 입방체 구조의 두 가지 요소로 표시됩니다. Shannon 엔트로피[34]와 관련된 다른 복잡도 측정은 모든 요소에 대한 이 측정이 동일하게 0이기 때문에 유용하지 않다고 언급했습니다.
마법 공식을 결정하기 위한 "방법" 섹션에서 설명한 것과 유사한 방법을 토폴로지 인덱스를 설명하는 마법 공식에 적용할 수 있습니다. 여기에서만 다항식의 차수가 7, 8 또는 9이므로 최소 10개의 연속 n에 대한 값 - 값을 계산해야 합니다. 그런 다음 더 높은 차수의 보간 문제가 결과를 제공합니다. 기호 도구 상자로 10×10 크기의 선형 시스템을 푸는 데 시간이 걸리므로 위상 지수에 대한 모든 계수는 모든 다항식의 계수를 얻기 위해 여러 개의 우변을 사용하여 동시에 계산할 수 있습니다.
토폴로지 인덱스에 대한 매직 공식은 표 23, 24, 25에 자세히 설명되어 있습니다. 우리가 분석하는 4가지 인덱스는 n에만 의존합니다. , 클러스터의 셸 수입니다. 결과를 보면 가장 복잡한 구조인 단순 3차 격자도 "가장 단순한" 공식을 가지고 있습니다. 우리의 노력에도 불구하고 bcc 큐브의 Szeged 인덱스를 풀 수 없습니다. 안정적인 솔루션을 찾지 못했습니다. 일반적으로 fcc 구조는 위상 공식에 대해 더 쉽게 풀 수 있습니다. 우리는 hcp 구조를 풀 수 없었고 몇 개의 bcc 구조만 풀 수 있었습니다. 이것은 fcc 격자가 bcc 또는 hcp보다 간단하기 때문에 토폴로지 복잡성과 관련이 있을 수 있습니다(표 22 참조). 표 내에서 cuboctahedron, 20면체 및 decahedron에 대한 공식을 제공합니다. 우리는 이전에 [12]에서 이러한 인덱스에 대한 숫자 데이터 테이블을 제공했으며 [12]의 cuboctahedron은 다른 마법 숫자를 갖는다는 경고를 받았습니다. 여기서 우리는 표로 만들어진 데이터가 마법의 공식으로 간결하게 요약될 수 있음을 알 수 있습니다. 또한 인덱스의 다항식 차수는 3D 공간의 규칙을 따릅니다[14]. Platonic solids에 대한 일부 위상 지수는 이전에 발표되었습니다[36]. 이 참조에서 n에 대한 5개의 모든 고체에 대한 Wiener 지수를 확인합니다. =1. fcc 격자의 단위 셀 행에 대한 Wiener 인덱스가 연구되었지만[37], 클러스터를 연구하기 때문에 결과를 비교할 수 없습니다.
다양한 클러스터의 표면 원자(분산, FE)의 비율이 그림 2에 나와 있습니다. 백금 나노클러스터는 크기와 모양에 따라 달라지는 산소 환원 반응(ORR)과 관련하여 촉매 활성이 있는 것으로 알려져 있습니다[38]. 이 참고문헌은 2.2 nm 크기의 백금 정육면체 클러스터가 최대 ORR 활성을 갖는 것으로 결정했습니다. PtNi 합금의 경우 (111) 표면이 ORR에 더 선호되는 것으로 알려져 있습니다[39]. d에서 FE에 대한 20면체, 8면체, 10면체 및 cuboctahedral 클러스터를 비교합니다. 관련 2.2 nm에서 백금의 경우 =7.5. 20면체, 8면체 및 10면체 클러스터에는 (111) 면이 있는 표면이 있습니다. 그림 2의 거듭제곱 법칙을 사용하여 주어진 d 관련 정이십면체 클러스터의 FE는 47.9%, 육팔면체의 경우 52.8%, 십이면체의 경우 57.5%이고 팔면체 클러스터의 FE=58.9% . 따라서 모양에 따라 팔면체 클러스터는 (111) 표면과 유사한 크기에 대해 가장 높은 FE 값을 모두 갖습니다. 거듭제곱 법칙 계수와 지수는 모두 작은 d에 대한 FE 결정과 관련이 있습니다. 관련 . 멱법칙 지수의 수학적 해석은 세로좌표 FE와 가로좌표 d의 관계로 물리적 의미를 부여합니다. 관련 또는 d의 상대적 백분율 변화에 대한 FE의 상대적 백분율 변화 관련 . 거듭제곱 법칙 계수는 d일 때 단순히 FE의 값입니다. 관련 =1.
<그림>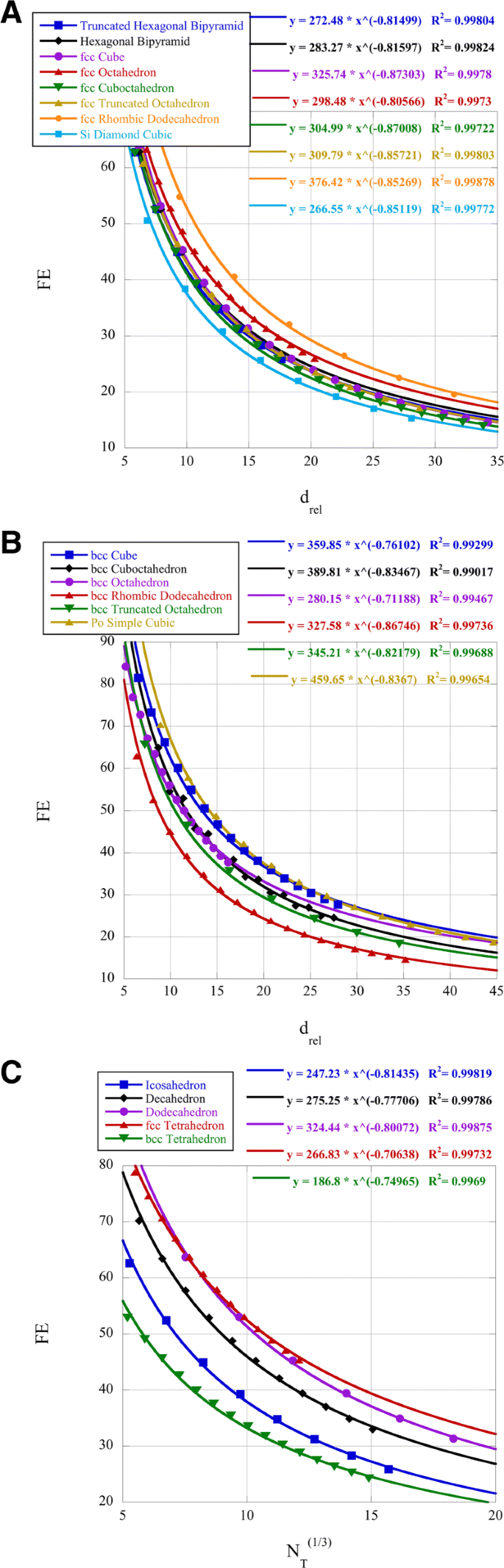
나노클러스터용 분산 FE
또 다른 연구 그룹은 백금 합금 20면체 클러스터를 합성하고 8면체 클러스터와 활성을 비교했습니다[40]. 이 나노클러스터는 크기가 약 13nm 또는 N이었습니다. =팔면체 클러스터의 경우 20,000 및 N 20면체 클러스터의 경우 =15,000 이것은 d를 생성합니다. 관련 8면체 클러스터의 경우 =30이고 20면체 클러스터의 경우 25입니다. 관련 거듭제곱 법칙을 사용하면 FE=18.0%가 됩니다. 8면체 클러스터의 경우 19.8%, 20면체 클러스터의 경우 19.8%입니다. 이 클러스터 크기에 대한 FE 차이는 거의 없지만 20면체 클러스터는 쌍정으로 인해 상당한 양의 변형이 있어 d-밴드 중심을 이동시켜 ORR 결과에 영향을 미칠 수 있습니다[40]. 그러나 [38]의 크기 종속 데이터가 주어지면 더 작은 클러스터가 훨씬 더 높은 ORR 데이터를 생성할 것이라고 제안할 수 있습니다. 실제로 4nm Pt3 Ni 8면체는 Mo로 도핑되었을 때 기록적인 높은 ORR 결과를 생성했습니다[41].
우리는 19가지 유형의 나노클러스터와 원자 수, 결합, 배위 수 및 위상 지수에 대한 몇 가지 관련 마법 공식을 연구했습니다. 여기에는 fcc, bcc, hcp, Platonic solids, diamond 입방체, 단순 입방체 및 십이면체 클러스터가 포함됩니다. 이러한 결과의 대부분은 이전에 결정된 것보다 더 상세하며 많은 수가 처음으로 열거됩니다. 재료 관련 연구의 가장 큰 목표는 구조와 특성의 상관관계입니다. 나노클러스터의 마법적 관계에 대한 이 상세한 연구는 그 방향으로 나아가는 단계입니다. 예를 들어 표면 원자의 분산과 촉매 활성과의 관계에 대한 논의가 있습니다. 이러한 결과가 과학자들이 나노클러스터 구조 및 관련 특성을 연구하는 데 도움이 되는 것이 우리의 의도입니다.
몸 중심 입방체
결정학적 정보 파일
면심 입방체
노출된 분수, 분산
육각형 밀착 포장
산화환원반응
역 위너 지수
세게드 인덱스
위너 지수
하이퍼 위너 지수
나노물질
복잡하고 혁신적인 디자인을 제공하는 풀 서비스 복합 재료 툴링 제조업체인 Symmetrix Composite Tooling(미국 브리스톨)은 2021년 3월 New York에서 열리는 제36회 Americas Cup에 대한 미국 도전자인 New York 요트 클럽 American Magic과 공급업체/기술 파트너십을 발표했습니다. 뉴질랜드. Symmetrix의 대형 CMS 포세이돈 5축 CNC 기계를 사용하여 회사는 American Magic의 AC75 포일링 모노헐 2개와 높이 26미터 높이의 마스트에 대한 패턴과 몰드를 생산했습
Gartner는 보고서에서 RPA 소프트웨어에 대한 시장의 힘과 주요 엔터프라이즈 공급업체를 조사합니다. RPA가 기업에서 매우 빠르게 채택되고 있다는 점을 감안할 때 2024년에는 24억 달러에 이를 것으로 추정되며, Gartner는 RPA 소프트웨어에 대한 최초의 Magic Quadrant를 출시할 때가 되었다고 말할 수도 있습니다. Gartner에 따르면 RPA는 시장으로서 2018년 총 수익이 8억 5천만 달러 미만으로 여전히 상대적으로 작지만 공식적으로 추적하는 가장 빠르게 성장하는 소프트웨어 하위 부문이며 전년 대비