나노물질








현재 이중 인터페이스 자기 터널 접합(MTJ)은 나노 규모 기술 노드에서 열 안정성 장벽을 향상시키기 위해 개발되었습니다. Dzyaloshinskii-Moriya 상호 작용(DMI)은 중금속/강자성 구조의 사용으로 인해 이러한 장치에 필연적으로 존재합니다. 이전 연구에서는 기존의 단일 인터페이스 STT(스핀 전달 토크) MTJ에 대한 DMI의 해로운 영향이 입증되었습니다. 여기에서 우리는 이중 인터페이스 STT-MTJ에서 DMI의 해로운 영향이 거의 제거될 수 있음을 증명할 것입니다. 이러한 결론은 DMI에 대한 Ruderman-Kittel-Kasuya-Yosida(RKKY) 상호작용의 억제 효과에 기인합니다. 이론적인 모델과 마이크로 자기 시뮬레이션 결과를 기반으로 상세한 메커니즘을 분석합니다. 우리의 작업은 이중 인터페이스 STT-MTJ의 합성 자유 레이어에서 DMI를 적절하게 제어하는 것의 중요성을 강조합니다.
자기 랜덤 액세스 메모리(MRAM)는 저전력 소비, 고밀도, 빠른 액세스 속도, 거의 무한한 내구성 및 CMOS 기술과의 우수한 호환성 덕분에 차세대 비휘발성 메모리의 가장 유망한 후보 중 하나입니다[1, 2]. MRAM의 기본 장치는 MTJ(자기 터널 접합)로, 두 개의 강자성층(고정층 및 자유층) 사이에 샌드위치된 터널 장벽으로 구성됩니다. 수직 이방성의 발전을 통해 MTJ의 피처 크기는 40 nm 또는 1x nm 미만으로 축소되었습니다[3,4,5]. 그러나 sub-40 nm MTJ의 과제는 적절한 열 안정성 장벽 E을 유지하는 것입니다. =μ 0 엠 s 안 ㅋ V /2. (μ 포함 0 진공 자기 투자율, M s 포화 자화, H ㅋ 이방성 필드, V 자유층의 부피). 이 방정식이 나타내는 바와 같이, E MTJ의 스케일링에 따라 감소하여 데이터 보존 시간이 단축됩니다. 이 문제를 극복하기 위해 충분히 높은 E를 달성하기 위한 이중 인터페이스 MTJ가 제안되었습니다. sub-40 nm 기술 노드에서 [6,7,8,9,10]. 복합 자유층으로 두 개의 결합된 강자성층을 사용함으로써 등가 체적(V ) 이중 인터페이스에서 MTJ는 열 안정성 장벽을 향상시키기 위해 증가됩니다. 한편, 낮은 스위칭 전류를 유지하기 위해 감쇠 상수가 감소합니다.
이중 인터페이스 MTJ에서 강자성체/중금속(FM/HM) 구조는 성능 최적화에 중요한 역할을 합니다. 한편, FM/HM 구조는 스핀-궤도 결합(SOC)을 증가시켜 수직 이방성을 유도합니다. 반면에 중금속은 복합 자유층의 두 강자성층 사이에 스페이서로 작용하여 Ruderman-Kittel-Kasuya-Yosida(RKKY) 상호작용을 제공합니다[11]. 동일한 레이어처럼 작동하도록 합니다. 게다가, 최근 연구는 강자성체의 원자 스핀과 결합하는 중금속의 강한 SOC가 Dzyaloshinskii-Moriya 상호작용(DMI)이라고 불리는 비대칭 교환 결합을 형성할 수 있음을 보여줍니다[12, 13]. 따라서 DMI는 FM/HM 구조의 이중 인터페이스 MTJ에서 자연스럽게 유도됩니다. DMI는 키랄 자기 질감(예:스핀 나선, 스커미온 및 Neel-유형 도메인 벽)을 선호하고 최근 연구에 의해 검증된 바와 같이 자화 역학에 극적으로 영향을 미칩니다. ,22,23,24,25]. 두 개의 FM/HM 인터페이스를 추가 RKKY 상호 작용과 함께 고려해야 하기 때문에 DMI의 역할이 이중 인터페이스 MTJ에서 더 복잡해질 것이라는 점을 언급하는 것이 중요합니다. 따라서 DMI가 이중 인터페이스 MTJ에 미치는 영향을 밝히는 것이 중요합니다.
이 편지에서 우리는 처음으로 DMI와 RKKY 상호 작용의 작용에 따라 이중 인터페이스 MTJ의 전환 과정을 연구합니다. 이중 인터페이스 MTJ는 MRAM의 데이터 쓰기를 위한 주류 접근 방식인 STT(스핀 전달 토크)에 의해 전환됩니다. DMI가 STT 스위칭에 해로운 영향을 미친다는 것이 최근 보고되었다[21, 22]. 여기에서 우리의 결과는 이중 인터페이스 MTJ에서 DMI의 해로운 영향이 RKKY 상호 작용에 의해 억제되어 빠른 스위칭과 보다 균일한 역학을 초래할 수 있음을 보여줍니다. 우리의 작업은 부정적인 계면 효과에 대한 이중 인터페이스 STT-MTJ의 견고성을 증명합니다.
이 작업에서 연구된 장치는 합성 자유층으로 FM/HM/FM 구조를 사용하여 그림 1a에 나와 있습니다. HM 층 두께는 유도된 RKKY 상호작용이 두 개의 FM 층을 강자성적으로 결합하도록 적절한 값으로 조정된다. FM 층 중 하나는 자기적으로 더 부드럽고 FL1(자유 층 1)로 표시되는 반면 다른 하나는 자기적으로 더 단단하고 FL2(자유 층 2)로 표시됩니다. 복합 자유층의 자화를 전환하기 위해 이중 인터페이스 MTJ에 전류를 인가하고 STT를 생성합니다. 이 작업에서는 참조 레이어에서 FL1으로 전송된 STT만 고려하는 반면 FL1과 FL2 사이의 다른 토크는 무시됩니다. 이 단순화된 모델은 이전에 보고된 작업[26,27,28]과 일치합니다. DMI는 FM/HM 및 HM/FM 인터페이스 모두에서 유도되며 다른 키랄성으로 인해 반대 부호를 갖습니다[29].
<그림>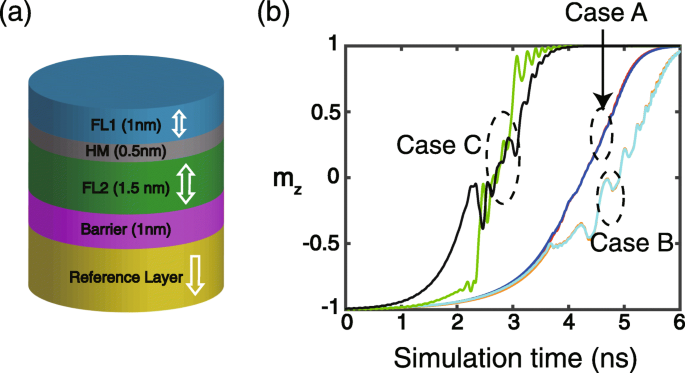
아 이 작업에서 연구된 장치의 도식적 구조. 다른 레이어는 명확성을 위해 표시되지 않습니다. ㄴ 시간 종속 m의 일반적인 결과 z (단위 자화의 수직 성분). 사례 A:σ =1 × 10 −3 J/m 2 , 디 1 =디 2 =0(FL1의 경우 빨간색, FL2의 경우 파란색). 사례 B:σ =1 × 10 −3 J/m 2 , 디 1 =1 mJ/m 2 , 디 2 =−1 mJ/m 2 (FL1의 경우 주황색, FL2의 경우 청록색). 사례 C:σ =1 × 10 −4 J/m 2 , 디 1 =디 2 =0(FL1의 경우 녹색, FL2의 경우 검정색)
이중 인터페이스 MTJ에서 FL1 및 FL2의 자화 역학은 마이크로 자기 시뮬레이션에 의해 연구됩니다. 단위 자화 벡터의 시간 진화는 다음 Landau-Lifshitz-Gilbert(LLG) 방정식에 의해 제어됩니다. 우리는 소자 구조를 모델링하고 자화 역학 분석을 위한 LLG 방정식을 풀기 위해 오픈 소스 마이크로자기 시뮬레이션 도구인 OOMMF 패키지를 선택했습니다[30].
$$ \frac{\partial \mathbf{m}}{\partial t}=-\gamma \mathbf{m}\times {\mathbf{H}}_{eff}+\alpha \mathbf{m}\times \frac{\partial \mathbf{m}}{\partial t}+\gamma \frac{\mathrm{\hslash}}{2e}\frac{\eta }{M_s{t}_F}J\mathbf{m }\times \left(\mathbf{m}\times \mathbf{z}\right) $$여기서 γ 는 자이로마그네틱 비율, m 자화에 따른 단위 벡터, z 두께 방향의 단위 벡터, H 에프 는 단축 수직 이방성, 6-이웃 교환 에너지, DMI 필드, RKKY 상호 작용, 자기 소거 필드, 쌍극자 상호 작용 및 STT를 포함하는 유효 필드입니다. 다른 매개변수와 기본값은 달리 명시되지 않는 한 표 1에 나열되어 있습니다. 이 매개변수 값은 최신 기술에 따른 것입니다. DMI 크기에 관해서는 이중 인터페이스 MTJ에서 CoFeB/W/CoFeB 복합 자유층을 고려합니다[10, 31, 32, 33]. 보고된 W/CoFeB의 실험적 DMI 결과는 0.12mJ/m 2 에서 다양합니다. ~ 0.73mJ/m 2 [34,35,36]. 시뮬레이션에서 DMI 크기 범위를 ±2mJ/m 2 로 확장합니다. 일반 연구용입니다.
한 쌍의 자기 모멘트 사이의 RKKY 에너지 m 나 그리고 m j E로 정의됩니다. 이 =σ [1 − m 나 ∙ m j ]/∆ 이 , 여기서 m 나 그리고 m j 는 각각 FL1 및 FL2의 자기 모멘트입니다. σ 는 두 표면 간의 쌍선형 표면 교환 계수입니다. ∆ 이 셀 i 방향의 재량 셀 크기입니다. 셀 j 쪽으로 . 이 작업에서 FL1과 FL2는 강자성으로 결합된 다음 σ> 0은 RKKY 상호작용이 m을 만드는 경향이 있음을 의미합니다. 나 m에 평행 j . DMI는 인접한 원자 스핀 S에 작용합니다. 1 및 S 2 SOC가 큰 세 번째 원자를 통해. 해당 DMI Hamiltonian은 H로 표시됩니다. DM =− D 12 ∙ (S 1 × S 2 ), 여기서 D 12 는 DMI 벡터[37]입니다. 따라서 DMI는 S 1 및 S 2 , RKKY 상호 작용과 경쟁합니다.
먼저 시간에 따른 m의 전형적인 시뮬레이션 결과 z (단위 자화의 수직 성분)은 그림 1b에 나와 있습니다. RKKY 상호작용이 충분히 강한 경우(예:σ =1 × 10 −3 J/m 2 A와 B)의 경우 FL1과 FL2가 함께 결합되어 있으므로 DMI를 고려하든 안 하든 자화 역학은 거의 동일합니다. 또한 DMI의 도입은 보고된 결과[21,22,23]와 일치하고 DMI의 비대칭 교환에 기인할 수 있는 자화 전환 과정을 왜곡하는 것으로 나타났습니다(사례 B 참조). RKKY 상호 작용이 충분히 강하지 않으면 FL1과 FL2의 자화 역학이 이상적으로 결합되어 둘 사이의 상당한 차이가 관찰될 수 없습니다(사례 C 참조). 아래에서 시뮬레이션 결과는 달리 명시되지 않는 한 충분히 강한 RKKY 상호 작용에서 얻은 것입니다.
이후 다양한 RKKY 상호작용에 따른 스위칭 속도를 연구한다. 스위칭 속도는 m z 0에 도달합니다(전환 시간으로 정의됨). 디 1 그리고 디 2 는 각각 양수와 음수 값으로 설정됩니다[29]. 해당 결과는 그림 2에 나와 있습니다. DMI가 없는 경우, 다른 보고된 결과와 일치하여 향상된 RKKY 상호 작용으로 전환 시간이 증가합니다[26,27,28,38]. 그 이유는 더 강한 RKKY 상호 작용이 FL1과 FL2의 자화 역학을 더 일관되게 만들어 복합 자유층의 이방성을 동등하게 증가시키기 때문입니다. 그러나 RKKY 강도에 대한 전환 시간의 의존성은 DMI가 있는 경우 더욱 혼란스러워집니다. 이 혼돈은 주로 FL1과 FL2 사이의 이방성의 불일치에 기인합니다. 자세한 설명은 나중에 보여드리겠습니다. 이러한 결과는 이중 인터페이스 MTJ의 스위칭 동작에 대한 DMI의 무시할 수 없는 영향을 입증합니다.
<그림>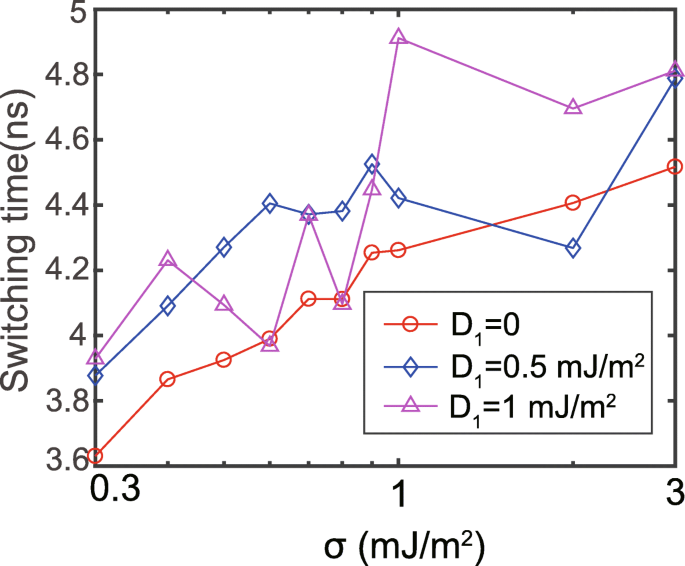
RKKY 강도의 함수로서의 스위칭 시간, σ는 로그 눈금으로 표시됩니다. 디 1 그리고 디 2 동일한 값으로 설정되지만 부호는 반대입니다.
다음으로 DMI의 효과를 보다 자세히 연구한다. 그림 3은 DMI 강도의 함수로서의 스위칭 시간을 보여줍니다. D 1 그리고 디 2 실제로는 반대 부호를 가지지만 의도적으로 그림 3a에서 동일한 양의 값으로 설정됩니다. 즉, Fig. 3a는 시뮬레이션 모델 검증을 위해 연구한 가상의 경우에 해당한다. 물리 이론의 관점에서, 두 개의 긍정적인 DMI의 해로운 영향은 강자성 결합 RKKY 상호 작용의 작용으로 누적됩니다. 따라서 D가 증가함에 따라 스위칭 시간이 증가할 것으로 예상됩니다. 1 그리고 디 2 , 이전 연구에서 보고된 바와 같이 [21, 22]. 이 분석은 그림 3a에 표시된 결과와 잘 일치합니다. 따라서 시뮬레이션 모델의 합리성이 검증됩니다. 그림 3a와 달리 DMI의 해로운 영향은 D 1 그리고 디 2 그림 3b와 같이 반대 부호를 가지며 스위칭 시간의 변화는 그림 3a에 비해 훨씬 작습니다. 그림 3b에서 곡선은 정확히 단조롭지 않으며 국부적 변동은 나중에 설명됩니다. 놀랍게도, 두 인터페이스에서 DMI의 영향은 D의 크기를 적절하게 조정하여 상쇄될 수 있습니다. 1 그리고 디 2 , 도 3c에 도시된 바와 같이. 이러한 결과는 다음과 같이 키랄성 이론으로 설명할 수 있습니다.
<그림>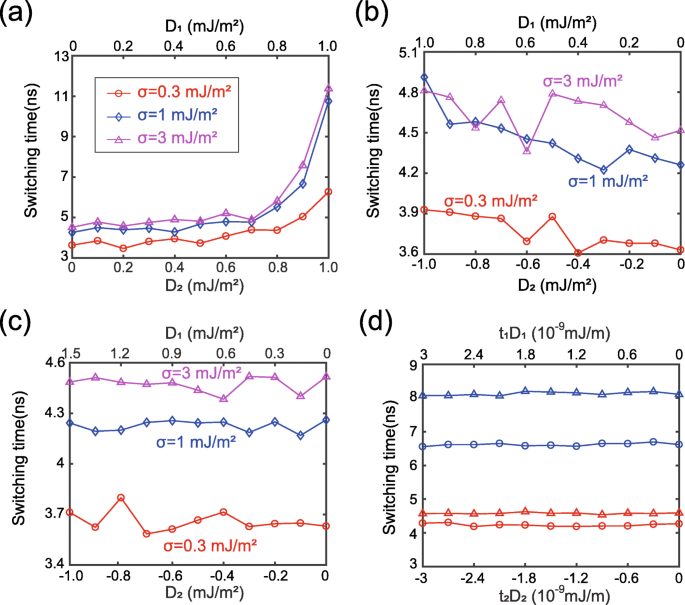
DMI 강도의 함수로서의 스위칭 시간. 아 디 1 그리고 디 2 동일한 양수 값으로 설정됩니다. ㄴ 디 1 그리고 디 2 동일한 값으로 설정되지만 부호는 반대입니다. ㄷ 디 1 그리고 디 2 t를 충족하도록 구성됩니다. 1 디 1 + 그 2 디 2 =0. d t를 유지하면서 두께 또는 이방성 상수를 변경하는 동안 추가 결과 1 디 1 + 그 2 디 2 =0. 파란색 선:t 1 2 nm로 변경됩니다. 빨간선:t 1 1.5 nm로 변경됩니다. 삼각형 데이터:σ =3 × 10 −3 J/m 2 . 원 데이터:σ =1 × 10 −3 J/m 2
DMI 에너지는 E로 표현됩니다. DM =그 ∬ 디 [나 x (∂m z /∂x ) − m z (∂m x /∂x ) + m 와 (∂m z /∂y ) − m z (∂m 와 /∂y )]d 2 r =tDε DM [39], 여기서 D 연속 DMI 상수, t 는 강자성층의 두께이다. 위에서 언급했듯이 FL1과 FL2의 자화 역학은 충분히 강한 RKKY 상호 작용에서 거의 동일합니다. 이 경우 동일한 ε DM FL1 및 FL2에서 얻습니다. 그러면 FL1과 FL2의 총 DMI 에너지는 E로 계산할 수 있습니다. 너무 =(t 1 디 1 + 그 2 디 2 )ε DM . 따라서 D를 설정하여 1 /디 2 =− t 2 /그 1 , FL1 및 FL2의 DMI 효과는 충분히 큰 σ의 경우 그림 3c와 일치하여 완전히 상쇄될 수 있습니다. 이 결론은 D를 유지하는 동안 다른 매개변수가 의도적으로 변경되는 그림 3d에 표시된 추가 결과에 의해 추가로 확인됩니다. 1 /디 2 =− t 2 /그 1 .
등가 DMI 크기(D eq )는 합성 자유층의 D로 표현될 수 있습니다. eq =(t 1 디 1 + 그 2 디 2 )/(그 1 + 그 2 ), 이중 인터페이스 MTJ에 대한 DMI의 영향을 정량적으로 분석하는 데 사용할 수 있습니다. 이 방정식의 유효성을 검증하기 위해 그림 4a에 두 그룹의 시뮬레이션 결과를 보여줍니다. 여기서 두 개의 곡선은 동일한 D eq 그러나 서로 다른 두 쌍의 {D 1 , 디 2 } 값. 두 곡선 사이에는 약간의 차이가 있지만 전반적인 경향은 유사하며 STT 스위칭에 대한 DMI의 해로운 영향을 검증합니다. 여기서 두 곡선의 차이는 다음과 같이 설명할 수 있다. FL1과 FL2는 서로 다른 이방성 상수를 가지므로 그림 4c와 같이 자화 역학의 국소적인 불확실한 진동을 유발합니다. 도 2 및 도 3b에서도 동일한 현상이 관찰된다. 대신 FL1 및 FL2의 이방성 상수가 동일한 값으로 설정된 이상적인 경우가 그림 4b, d에 나와 있습니다. 분명히, 두 곡선 사이에 좋은 일치가 나타나 위의 D 표현을 나타냅니다. eq 이중 인터페이스 MTJ의 동등한 DMI 효과를 잘 설명할 수 있습니다.
<그림>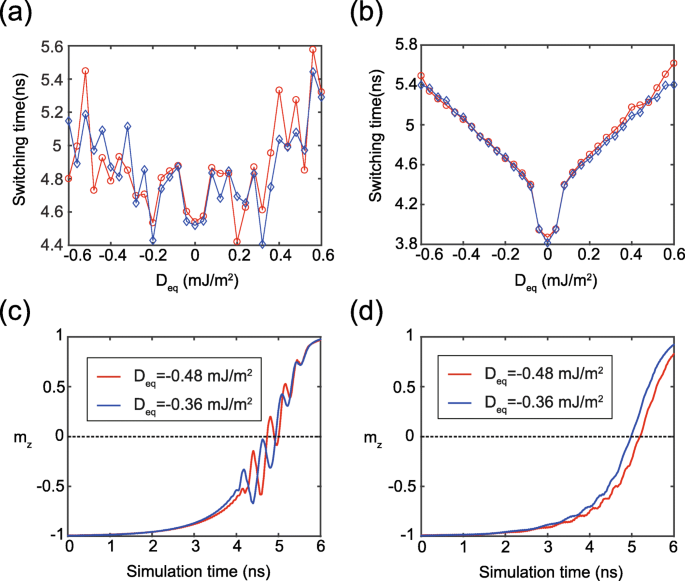
아 , b D의 함수로서의 스위칭 시간 eq . 각 D eq 서로 다른 두 쌍의 {D 1 , 디 2 } D에 따른 값 eq =(t 1 디 1 + 그 2 디 2 )/(그 1 + 그 2 ). 빨간색 곡선:D 1 한편 D 2 1mJ/m 2 로 고정 . 파란색 곡선:D 1 그리고 디 2 항상 같은 값으로 설정됩니다. 여기서 σ =1 × 10 −2 J/m 2 . a에서 , 다른 매개변수는 표 1과 같이 구성됩니다. b , 케이 u 1 =케이 u 2 =0.7mJ/m 3 이상적인 경우. ㄷ , d 시간 종속 m의 일반적인 결과 z a에 해당 그리고 b , 각각
마지막으로, 우리는 자화 역학의 시간 진화를 더 자세히 분석합니다. 그림 5는 자화 스위칭 동안 시간에 따른 에너지를 보여줍니다. FL1 및 FL2의 DMI 에너지는 D의 부호와 크기에 따라 누적되거나 취소됩니다. 1 그리고 디 2 . 이러한 경향은 위의 이론적 모델과 잘 일치합니다. 또한 RKKY 에너지는 낮은 값으로 유지되어 FL1 및 FL2의 자기 모멘트가 동기적으로 구동됨을 확인합니다. RKKY 및 DMI 필드의 분포는 그림 6에 나와 있으며, 여기서 RKKY 필드는 다양한 경우에 서로 다른 역할을 합니다. 첫째, 0이 아닌 DMI의 경우(케이스 2 및 케이스 3 참조), RKKY 필드는 DMI가 0인 경우(케이스 1 참조)에 비해 훨씬 강합니다. RKKY 필드는 DMI가 있는 상태에서 자성 텍스처의 추가적인 불균일성을 극복해야 함을 이해할 수 있습니다. 둘째, D인 경우 1 그리고 디 2 부호가 반대인 경우 RKKY 필드는 FL1 및 FL2 모두에서 DMI 필드에 저항합니다(사례 2 참조). 결과적으로 DMI가 약해져서 자화 역학이 보다 균일해집니다. 대조적으로, 한 번 D 1 그리고 디 2 동일한 부호를 가지면 RKKY 필드는 한 강자성 층에서 DMI 필드에 저항하지만 다른 강자성 층에서는 DMI 필드를 돕습니다(사례 3 참조). 따라서 전체 DMI 필드는 여전히 자화 역학에 일정한 영향을 미치므로 D 1 그리고 디 2 같은 기호입니다.
<그림>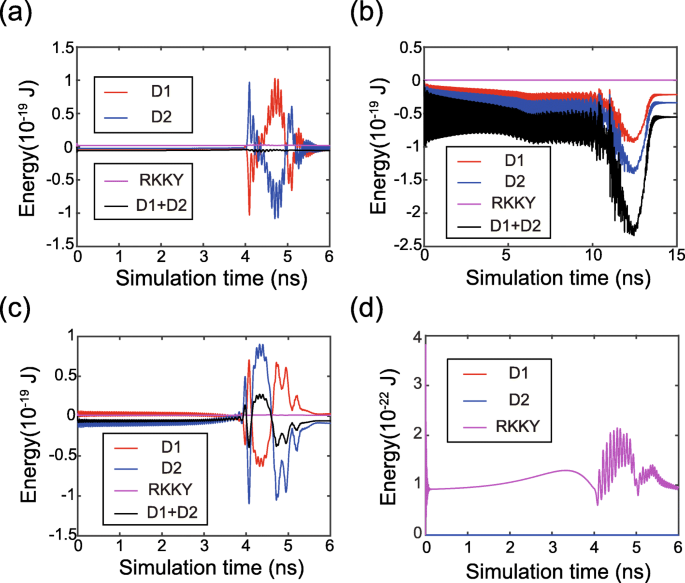
DMI 및 RKKY 에너지의 시간 진화. 아 디 1 =1.5mJ/m 2 , 디 2 =− 1mJ/m 2 , 즉 DMI 효과가 취소됩니다. ㄴ 디 1 =디 2 =1mJ/m 2 , 즉 DMI 효과가 누적됩니다. ㄷ 디 1 =1mJ/m 2 , 디 2 =− 1mJ/m 2 즉, DMI 효과가 완화되지만 상쇄되지는 않습니다. d 디 1 =디 2 =0
<그림>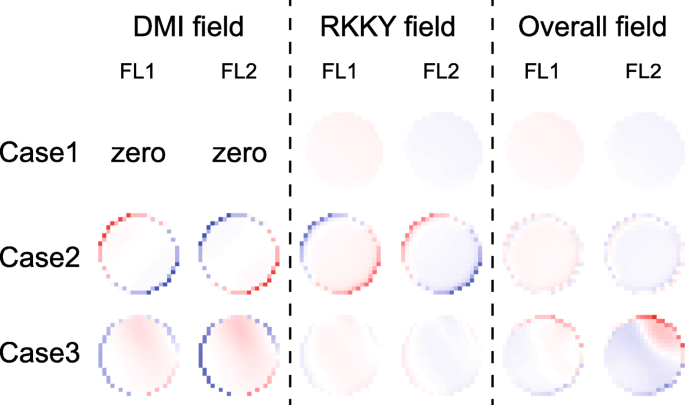
DMI 및 RKKY 필드의 공간 분포. 여기에 각 경우에 대해 한 시점의 일반적인 결과가 표시됩니다. 결론은 다른 순간에도 변하지 않습니다. 사례 1:D 1 =디 2 =0. 사례 2:D 1 =1.5mJ/m 2 , 디 2 =− 1mJ/m 2 , 즉, DMI 효과가 취소됩니다. 사례 3:D 1 =디 2 =1mJ/m 2 , 즉 DMI 효과가 누적됨
그림 7은 자화 스위칭 동안 FL1 및 FL2의 마이크로 자기 구성을 보여줍니다. 모든 경우에 영역 벽이 나타나지만 때때로 다른 기능이 관찰될 수 있습니다. DMI가 불균일한 자기 질감을 선호한다는 것은 잘 알려져 있습니다. 그럼에도 불구하고, Fig. 7에서 DMI가 존재하는 경우에도 균일한 자화가 여전히 형성된다(m 시간 참조). z =− 0.5(2)의 경우 DMI 효과가 상쇄됩니다. 다시 말하지만, 이 결과는 위의 이론적 모델을 검증합니다. 또한, D 1 그리고 디 2 위의 분석과 일치하는 동일한 부호입니다(영역 벽이 항상 나타나는 경우 3 참조). 또한 더 작은 MTJ로 시뮬레이션된 일부 결과를 보여줍니다(그림 7의 마지막 두 행 참조). 케이스 2(DMI가 상쇄됨)와 케이스 3(DMI가 상쇄되지 않음)의 마이크로자성 구성의 차이가 더 두드러집니다.
<사진>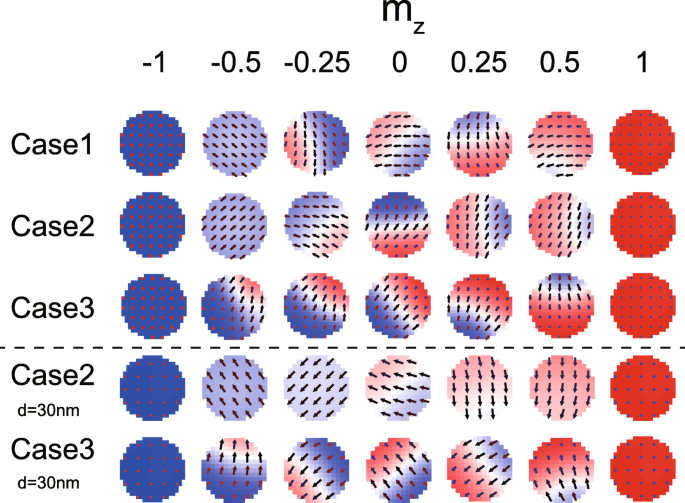
자화 스위칭 중 마이크로 자기 구성. 여기에서 Case 1~3은 그림 6과 같은 파라미터로 설정되어 있습니다.
우리는 이중 인터페이스 STT-MTJ에 대한 DMI의 영향을 종합적으로 연구했습니다. 잘 알려진 바와 같이 이중 인터페이스 MTJ는 열 안정성 장벽을 향상시키기 위해 개발되었습니다. 이 연구에서 우리의 결과는 DMI의 해로운 영향을 억제하는 이중 인터페이스 MTJ의 또 다른 이점을 증명합니다. 두 개의 강자성 층에 있는 DMI는 적절한 값과 반대 부호로 구성된 경우 억제되거나 심지어 상쇄될 수 있으며, 이는 이중 인터페이스 STT-MTJ 구조에 의해 자연스럽게 충족됩니다. 결론을 설명하기 위해 이론적 모델이 제안되었습니다. 자화 역학에서 DMI의 역할을 밝히기 위해 마이크로 자기 시뮬레이션 결과가 논의되었습니다. 우리의 작업은 이중 인터페이스 STT-MTJ에서 DMI를 최소화하는 실행 가능한 접근 방식을 제공합니다.
모든 데이터는 제한 없이 완전히 사용할 수 있습니다.
Dzyaloshinskii-Moriya 상호 작용
자유 레이어
강자성체/중금속
자기 랜덤 액세스 메모리
자기 터널 접합
Ruderman–Kittel–Kasuya–Yosida
스핀-궤도 커플링
스핀 전달 토크
나노물질
Fortify(미국 매사추세츠주 보스턴)는 Josh Martin(Fortify의 CEO)과 보스턴 노스이스턴 대학교 DAPS 연구소 소장인 Randall Erb의 복합 3D 프린팅 연구를 기반으로 2016년에 설립되었습니다. (Erb는 Boston Materials와 Fortify의 공동 설립자이기도 합니다.) 그들의 목표는 최적화된 미세 구조로 복합 재료를 빠르게 생산할 수 있도록 하는 것이었습니다. 그들이 개발한 특허받은 Fluxprint 기술은 자기장과 DLP(디지털 광 처리)를 사용하지만 고충진 수지 시스템을 사용하여 고해상
그립 토크:잘못된 질문에 대한 답변. 2부 시리즈 중 2부 (그리핑 토크:이것이 도구/도구 홀더 효율성을 측정하는 올바른 방법입니까? 참조). 금속 가공용 기계가 점점 더 빨라지면서 우리가 공구 보안이라고 부르는 것에 대한 탐구도 계속되었습니다. 새로운 형태의 도구 홀더가 사용되면서 그립 토크는 최고의 생산성을 위해 도구를 제자리에 유지하기 위해 다양한 방법을 판단하고 비교하는 데 계속 선호되는 방법이었습니다. 사이드락 엔드밀 척 사이드록 척은 도구의 보안을 보장하기 위한 초기(거의 100년 전) 솔루션이었습니다