최적화된 반사율 면 코팅에 의한 분산 피드백 양자 캐스케이드 레이저의 안정적인 단일 모드 작동

방법

이론 및 시뮬레이션

유한 DFB 캐비티에서 반사 방지 코팅 효과에 대한 시뮬레이션의 핵심은 두 개의 밴드 에지 모드에 대한 모드 손실 계산입니다. Transfer Matrix 방법은 전체 레이저 구조를 분석하는 적절한 방법이 될 것입니다[16, 17]. 우리는 이 방법을 그림 1에 표시된 것과 유사한 길이 방향 굴절률 프로파일을 갖는 장치에 적용하는 것을 고려합니다. 이 개략도는 서로 다른 유효 굴절률 섭동(n)이 작은 격자의 효과를 보여줍니다. _eff,1 , n _에프,2 ) 및 코팅 필름(n ₃ , n ₄ ) 안내 모드에서. 계산에 사용된 주재료의 복소굴절률은 InP(3.088 + i*2e−4), InGaAs(3.4 + i*2.9e−5), 활성영역(3.298 + i*4e−5), 고농도 InP(2.81 + i*1.4e−2), SiO₂ (1.3603 + i*6.3e−4), Au(1.341 + i*32.582), Al₂ O₃ (1.5348 + i*3.2967e−3) 및 Ge(4.0165 + i*4e−2). 그런 다음 서로 다른 유효 인덱스 n _eff,1 =3.1599 + i*5.17e−5 및 n _eff,2 =3.1662 + i*5.6756e−5는 편미분방정식(PDE) 함수를 통해 COMSOL로 계산되었습니다. 레이저는 단일 가로 모드에서 작동되어 레이저 공동을 따라 각 지점에서 빛의 전파 특성이 단일 스칼라 복소수 k로 설명된다고 가정합니다. , 이는 매질의 파동 벡터입니다. 레이저가 선형으로 편광되고 관련 전기장이 사인파 시간 의존성을 갖는 것으로 추가로 고려됩니다. e ^{나 ωt} . 위에서 주어진 이러한 가정에 따라 1차원 평면 전자기파 계수 E _z , 파동 함수의 특수 변형 부분을 설명하는 Helmholtz 방정식을 만족합니다.

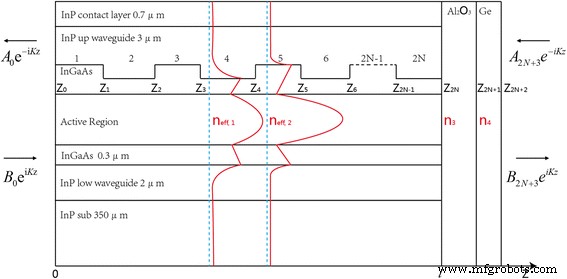
세로 광학 모드 프로파일에 반사 방지 코팅이 된 유한 DFB 캐비티 모델을 보여주는 개략도

케이 (z)는

여기서 ω 및 c 각 주파수와 광속 및 n은 각각 (z)는 레이저 공동을 따라 각 지점의 복소 굴절률입니다. 파동 벡터 k 해결해야 하는 문제는 두 부분으로 나눌 수 있습니다. k _r 그리고 k _나 . 실제 부분 k _r 허수 부분 k 동안 레이저 공동에서 빛의 파장을 결정합니다. _나 유한 캐비티의 모드 손실이 감쇠를 설명하기 때문에 발생합니다. 그림 1에서 레이저는 2N + 2 섹션, 여기서 N 는 격자 기간입니다. 각 섹션에서 전기장 E _n (z) 하나는 복소 진폭 A로 감소하는 2개의 역전파 기하급수적 평면파의 선형 조합입니다. _n 다른 하나는 B로 증가하고 있습니다. _n . 방정식은 다음과 같이 설명됩니다.

총 2N +개가 있습니다. 3개의 인터페이스. 이러한 각 경계면에서 전파 방향에 대한 전기장과 그 미분은 경계면의 양쪽에서 모두 같아야 합니다. 방정식은 다음과 같이 구합니다.

전송 매트릭스 M (d _n )에 의해 주어진다

전기적으로 펌핑된 레이저는 자체 발진 장치라는 점을 고려하면 장치 외부에서 들어오는 파동이 없습니다. 결과적으로 경계 조건 B ₀ =A _{2N + 3} =0이고 방정식은

파동 벡터 k의 각 값 식을 통해 Matlab의 도움으로 얻을 수 있습니다. (6). 허수부 k _나 캐비티 모드의 손실에 해당하는 것은 AR 코팅 효과를 분석하는 데 도움이 될 것입니다.

그림 2a는 전송 매트릭스 시뮬레이션을 기반으로 계산된 결과를 보여줍니다. 두 개의 빨간색 곡선에서 볼 수 있듯이 고주파 모드 손실은 반사율이 감소함에 따라 매우 느리게 변하는 반면 저주파 모드는 급격히 증가합니다. 삽입된 그림은 격자의 단일 기간 동안 저주파 및 고주파 모드에 대해 계산된 모드 프로파일을 보여줍니다. 플로팅된 바와 같이 저주파 모드는 격자의 더 높은 굴절률 부분인 격자 피크에서 더 높은 전기장 크기를 가지며, 또한 고주파수 모드는 격자의 하위 굴절률 부분에 더 집중됩니다. 면 반사율이 없는 무한 캐비티 모델의 경우 고주파 모드는 항상 저주파 모드보다 모드 손실이 낮습니다. 종단면 미러의 효과를 무시할 수 있는 경우 도파관 손실이 더 작은 고주파 모드는 항상 지연됩니다. 그러나 종단면 거울의 존재는 레이저 캐비티에서 DFB 모드를 건설적으로 또는 파괴적으로 간섭하는 반사를 제공합니다. 이 간섭은 각 모드의 유한 격자 캐비티 손실에 영향을 미치고 어떤 모드 레이저가 발생하는지 결정할 수 있습니다. 미러의 효과는 두 미러의 위치가 한 DFB 모드의 전기장 진폭 피크와 일치할 때 가장 크며, 이는 미러가 다른 DFB 모드의 노드에 있을 때도 마찬가지입니다. 여기에서 코팅되지 않은 패싯의 미러는 저주파 모드의 피크와 일치하고 엔드 미러의 반사는 레이저 캐비티에 존재하는 모드와 최대한 보강 간섭합니다. 그 결과 미러의 건설적인 기여로 인해 총 모드 손실이 감소합니다. 이중층 AR 코팅을 사용하여 반사율이 감소하고 추가적인 위상 편이 영향을 받음에 따라 약해진 간섭 효과와 증가된 미러 손실로 인해 반사율이 감소함에 따라 저주파 모드의 손실이 점차 증가했습니다. 한편, 강화된 간섭 효과로 인해 고주파 모드의 손실이 약간 변경되었습니다. 그 결과 Δ 모드 손실은 특히 전면 반사율이 <0.15일 때 지수 함수와 유사하게 수행됩니다. 시뮬레이션에 따르면 전면 면의 반사율이 <0.11일 때 전체 스펙트럼 내에서 하나의 최소 지점만 나옵니다. 이는 다른 대역 에지 모드 손실이 너무 높아서 레이즈할 수 없기 때문에 이론상 모드 홉이 발생할 수 없음을 의미합니다.

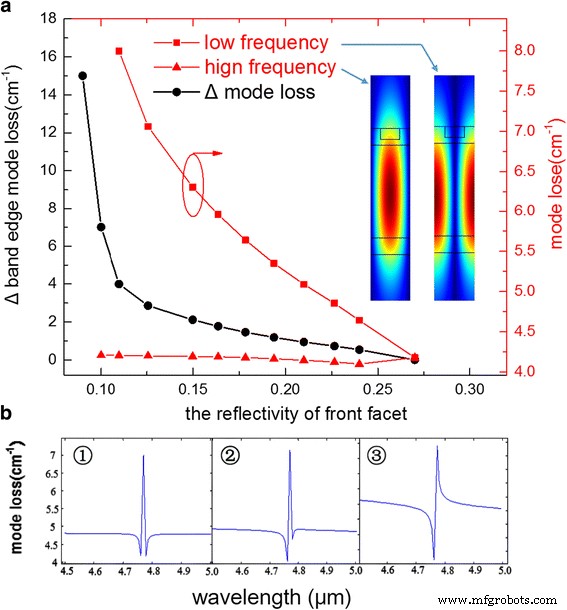
아 두 개의 빨간색 곡선은 각각 고주파 및 저주파 모드의 모드 손실입니다. 검은색 곡선은 Δ로 표시된 두 밴드 에지 모드 간의 차동 모드 손실입니다. 삽입된 그림은 격자의 단일 기간 동안 저주파 및 고주파 모드에 대해 계산된 모드 프로파일을 보여줍니다. ㄴ 다양한 AR 코팅을 사용한 전송 매트릭스 시뮬레이션을 기반으로 계산된 모드 손실 스펙트럼

그림 2b는 고주파 및 저주파 모드가 각각 4.762 및 4.779μm인 시뮬레이션 중 세 가지 일반적인 모드 손실 스펙트럼을 보여줍니다. 첫 번째는 AR 코팅이 없는 DFB-QCL입니다. 격자 피드백에서 비롯된 저지대역을 명확하게 볼 수 있으며 두 대역 에지 모드가 거의 동일합니다. 두 번째는 200nm Al₂를 사용한 특정 AR 코팅입니다. O₃ 및 0.22의 반사율을 갖는 5 nm Ge. 두 밴드 에지 모드 간의 차이가 분명해지기 시작합니다. 마지막 것은 반사율이 낮은 코팅에서 Δ 모드 손실이 너무 커서 저주파수 모드가 저지대역 손실 아래에 잠기는 것을 보여줍니다. 이론상 반사율이 낮을수록 Δ 모드 손실은 더 크지만 반사율이 매우 낮으면 장치에서 큰 미러 손실이 발생하여 WPE를 급격히 떨어뜨릴 수 있다는 점도 고려해야 합니다. 이는 실험에 따라 필름 두께를 선택하는 절충안입니다.

기기 제작

QCL 웨이퍼는 n-도핑된(Si, 3 × 10 ¹⁷ cm ⁻³ ) 2-포논 공명 설계에 기반한 고체 소스 분자 빔 에피택시(MBE)에 의한 InP 기판. 활성 코어에는 40단계의 변형 보상 In_0.669이 포함됩니다. Ga_0.331 As/In_0.362 알_0.638 Ref.와 유사한 양자 우물 및 장벽으로. [18]. 층 순서는 다음과 같았다:2-μm 하부 InP 클래딩 층(Si, 2.5 × 10 ¹⁶ cm ⁻³ ), 0.3μm 두께 일치 In_0.47 Ga_0.53 층으로 (Si, 4 × 10 ¹⁶ cm ⁻³ ), 40개의 활성/주사기 단계, 0.3μm 두께의 In_0.47 Ga_0.53 층으로 (Si, 4 × 10 ¹⁶ cm ⁻³ ), 3μm 상부 InP 클래딩 층(Si, 2.5 × 10 ¹⁶ cm ⁻³ ) 및 0.7μm 고농도 InP 클래딩 층(Si, 5 × 10 ¹⁸ cm ⁻³ ). 활성 영역의 평균 도핑 수준은 2.4 × 10 ¹⁶ 으로 실험적으로 조정되었습니다. cm ⁻³ . 매립 격자를 제작하기 위해 상부 클래딩을 상부 InGaAs 층까지 제거했습니다. 주기가 Λ =0.755 μm인 1차 DFB 격자(듀티 사이클 σ =20%)는 홀로그래픽 리소그래피 기술을 사용하여 300nm 두께의 상부 InGaAs 층에 정의된 후 습식 화학 에칭에 의해 약 90nm 깊이까지 에칭되었습니다. 그런 다음 3μm 두께의 저농도 도핑(Si, 2.5 × 10 ¹⁶ cm ⁻³ ) InP 레이어 다음에 0.2μm 점진적으로 도핑됨(1 × 10 ¹⁷ 에서 변경) cm ⁻³ ~ 3 × 10 ¹⁷ cm ⁻³ ) InP 층 및 0.5μm InP(5 × 10 ¹⁸ cm ⁻³ ) 접촉층은 금속 유기 기상 에피택시(MOVPE)에 의해 상부 클래딩으로 순차적으로 달성되었습니다.

격자 패턴 및 재성장을 구현한 후 에피 웨이퍼를 10μm 너비의 융기로 에칭한 다음 도파관을 MOVPE 시스템에 다시 도입하고 반절연 InP(Fe)에 묻었습니다. 450nm 두께의 SiO₂ 층은 리지 주변의 절연을 위해 플라즈마 강화 화학 기상 증착(PECVD)에 의해 증착되었고 전기 접촉은 Ti/Au 층에 의해 제공되었습니다. 추가로 5μm 두께의 금 층이 후속적으로 전기 도금되어 열 발산을 더욱 향상시켰습니다. 도파관은 2mm 길이의 막대로 절단되었으며 테스트는 반사율 패싯 코팅이 최적화된 장치에서 수행되었습니다. Al₂로 구성된 후면 양면 HR 코팅 O₃ /Ti/Au/Ti/Al₂ O₃ (400/5/100/10/200 nm) 및 Al₂로 구성된 전면 AR 코팅 O₃ /Ge(380/33 nm)는 전자빔 증발에 의해 증착됩니다. 계산된 전면 면의 반사율은 4.76μm 파장에 대해 3.4%이며, 코팅 두께의 변동과 반사율 사이의 자세한 관계는 이전에 발표된 논문[19]에서 논의되었습니다. 레이저는 인듐 땜납으로 SiC 방열판에 에피층 측면을 아래로 장착한 다음 외부 접촉 패드에 와이어 본딩했습니다. 스펙트럼 및 전기적 특성화를 위해 레이저를 펠티에 소자에 장착하고 서미스터를 사용하여 방열판에서 온도를 모니터링했습니다.

결과 및 토론

그림 3은 Bruker Vertex 70 FTIR 및 질소 냉각 HgCdTe 검출기로 측정된 증가하는 전류에 따라 전계발광에서 레이저로 동적으로 변경된 임계값 이하 방출 스펙트럼을 보여줍니다. 임계값 바로 위의 레이저 스펙트럼은 장치가 기본 모드에서 작동하고 전류가 285mA일 때 기본 모드의 저지대역을 명확하게 얻을 수 있음을 나타냅니다. 저지대역 폭 Δν에서 =3.076cm ⁻¹ 및 유효 색인 n _에프 =1/(2νΛ) =3.153, 결합 계수 κ를 계산합니다. =Δv ·π ·n _에프 =30.4cm ⁻¹ , 커플링 제품 κL에서 HR 코팅된 2mm 길이의 캐비티에 대한 결과 우리의 장치 제작과 잘 일치하는 12.1의. κL의 제품 이전의 이론적 조사보다 훨씬 큼 κL ≈ 1[20]은 overcoupled 방식을 취했음을 나타내며, 이는 전체 전류 및 검사 온도 범위 내에서 단일 모드를 확보하는 데 유리합니다.

<그림>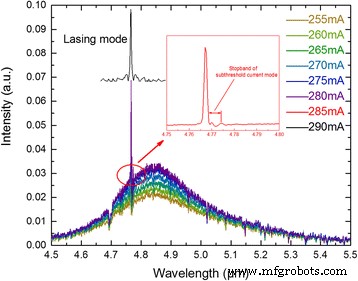

30 °C에서 측정된 장치의 하위 임계값 DC 스펙트럼

그림 4a는 일반적인 CW 전력-전류-전압(P -나 -V ) 20°C에서 90°C 사이의 다양한 방열판 온도에서 DFB 레이저의 곡선. 출력 전력은 0.65kA/cm ² 의 낮은 임계값 전류 밀도를 가진 2mm 길이 장치의 경우 200mW에 도달합니다. 20 ° C에서. 임계 전압(V _번째 )의 13.2-14.2 V는 20-90 °C의 온도 범위에서 측정되었습니다. 모드 홉은 P에서 쉽게 추론할 수 있는 60°C 미만의 낮은 방열판 온도에서만 존재한다는 점에 유의할 가치가 있습니다. -나 곡선. 높은 방열판 온도는 레이저 코어에 더 심각한 열 축적을 일으키므로 열 효과가 다른 모드 레이징을 억제하고 모드 홉이 발생하지 않습니다. 그림 4b는 P -나 -V 반사 방지(AR) 코팅이 전면에 증착된 DFB 레이저의 곡선과 3.4%의 AR 코팅 반사율을 선택합니다. 모든 부드러운 P -나 곡선은 우리가 측정한 온도 주변에 모드 홉이 존재하지 않음을 나타냅니다. 그림 4c, d는 25mA 간격으로 150~250mA의 다양한 전류에서 레이징 스펙트럼을 보여줍니다. 그림 4d에서 우리는 그림 4c의 모드 홉보다 최적화된 AR 패싯 코팅을 사용하여 다양한 전류 주위에서 안정적인 단일 모드를 달성한다는 것이 분명합니다. 주파수는 항상 주입 전류와 선형 관계를 유지하고 전류 조정 계수 Δν /Δ나 =− 0.024cm ⁻¹ mA ⁻¹ AR 코팅이 DFB-QCL의 모드 홉 문제를 해결하는 간단하고 효율적인 방법임을 증명합니다.

<그림>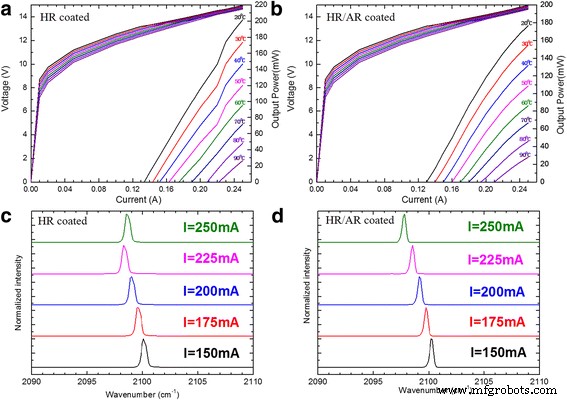

아 , b V와 함께 20~90°C의 다양한 방열판 온도에서 CW 모드로 작동되는 DFB 레이저의 출력 전력 대 전류 -나 곡선. ㄷ , d 20°C에서 25mA 단계로 150~250mA의 다양한 전류에서 CW 레이저 스펙트럼

그림 5는 20~90°C의 다양한 방열판 온도에서 코팅 DFB 레이저의 방출 스펙트럼을 보여줍니다. 측정은 0.25cm ⁻¹ 의 NICOLET 8700 FTIR 분광기를 사용하여 수행되었습니다. 빠른 스캔 모드에서 해상도. 90°C의 고온에서 측면 모드 억제 비율(SMSR)이 26dB인 조사된 전체 온도 범위에서 단일 세로 모드 방출이 관찰되었습니다. 도 5의 삽입도에서 보는 바와 같이 피크 방출 스펙트럼은 2100.4 cm ^-1 에서 이동하는 것으로 관찰되었다. 20°C ~ 2088.6cm ⁻¹ 에서 90 °C에서 온도 조정 계수 Δν에 해당 /ΔT =− 0.168cm ⁻¹ K ⁻¹ . 좋은 선형 튜닝은 방열판 온도가 변경되는 동안 모드 호핑이 발생하지 않았음을 나타냅니다. 또한 언급된 모든 장치는 능선 너비의 정확한 제어로 인해 기본 모드에서 CW 작동에서 지배적인 단일 측면 원거리장을 표시합니다.

<사진>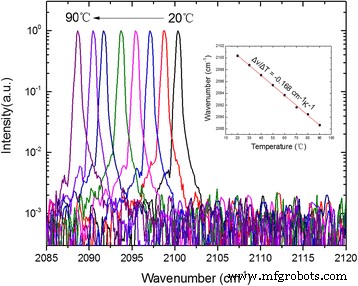

20–90°C의 다양한 방열판 온도에 대해 1.1 임계값 전류를 구동하는 DFB 레이저의 단일 모드 방출 스펙트럼. 인서트는 온도에 따른 레이저 주파수의 선형 맞춤 튜닝 특성을 보여줍니다.

CW WPE는 그림 6에 입력 전력 소비의 함수로 계산 및 표시되었습니다. 20°C에서 170mW의 출력 전력으로 약 240mA에서 4.7%의 최대 WPE를 얻었습니다. 최대 WPE는 여전히 50 및 90°C에서 각각 2.9 및 0.8%였습니다. 현재까지 이 값은 높은 재료 품질과 최적화된 반사율 패싯 코팅으로 인해 낮은 임계값 DFB-QCL에 대해 여전히 매우 높았습니다. WPE는 코팅 효과를 고려한 레이저 캐비티 길이의 최적화된 선택으로 더욱 향상될 수 있다고 믿어집니다.

<그림>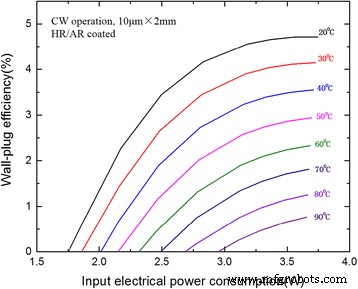

2mm 길이의 HR 및 AR 코팅된 DFB-QCL의 전력 손실에 따른 벽면 플러그 효율성

결론

λ에서 단일 모드 DFB-QCL의 실온 CW 작동을 시연했습니다. ~ 4.76μm. 이중층 유전체 Al₂로 구성된 AR 코팅을 증착하여 O₃ 전면의 Ge 및 모든 전류 및 온도 조건에서 모드 홉이 없는 안정적인 단일 모드가 성공적으로 구현되었습니다. 20°C에서 170mW의 높은 CW 출력 전력은 0.65kA/cm ² 의 매우 낮은 임계값 전류 밀도로 관찰되었습니다. . 이러한 장치는 실제 적용을 위해 중적외선 스펙트럼 범위에서 DFB-QCL의 안정적인 단일 모드 작동을 사용하기 위한 중요한 단계를 나타냅니다.

약어

AR:

반사 방지

BH:

묻힌 이종구조

CW:

연속파

DFB:

분산된 피드백

인사:

높은 반사율

MBE:

분자빔 에피택시

MOVPE:

금속 유기 기상 에피택시

PDE:

편미분방정식

PECVD:

플라즈마 강화 화학 기상 증착

P -나 -V :

전력-전류-전압

QCL:

양자 캐스케이드 레이저

문자 메시지:

사이드 모드 억제 비율

V _번째 :

임계 전압

WPE:

벽면 플러그 효율성

λ /4 추신:

1/4 파장 위상 편이

하이브리드 전-유전체-그래핀 메타표면에 기반한 제어 가능한 복굴절을 가진 편광 변환기 매우 빠르고 안정적인 전하 저장 성능을 나타내는 계층적 거대다공성 흑연 나노웹