원자 시뮬레이션은 탄탈륨(Ta) 전이 금속의 기계적 특성을 담당하는 물리적 메커니즘에 대한 통찰력을 제공할 수 있습니다. 분자 역학(MD) 방법을 사용하여 <100> 인장 하중을 통해 Ta 단결정의 탄성 특성의 온도 및 압력 의존성을 조사합니다. 먼저 Ta 단결정의 탄성 특성에 대하여 두 가지 EAM(embedded-atom method) 전위를 비교 연구하였다. 결과는 Ravelo-EAM(Physical Review B, 2013, 88:134101) 전위가 다양한 정수압에서 잘 작동함을 보여줍니다. 그런 다음 Ravelo-EAM 전위를 기반으로 하는 MD 시뮬레이션 결과는 Ta가 1K 온도에서 <100> 인장 하중 하에서 파괴되기 전에 체심 입방체(BCC)에서 면심 입방체(FCC)로의 상전이를 겪을 것임을 보여줍니다. , 그리고 모델 크기와 변형률 속도는 Ta의 인장 거동에 명백한 영향을 미치지 않습니다. 다음으로, 시스템 온도 1~1500K에서의 시뮬레이션 결과로부터 E의 탄성 계수가 다음과 같이 도출될 수 있습니다. 100 온도가 증가함에 따라 선형적으로 감소하는 반면, 항복 응력은 이차 다항식을 준수함에 따라 감소합니다. 마지막으로, 탄성 특성의 압력 의존성은 0에서 140GPa까지 수행되며 관찰 결과 전체적으로 압력이 증가함에 따라 탄성 계수가 증가하는 것으로 나타났습니다.
<섹션 데이터-제목="배경">일반적으로 탄탈륨(Ta)은 주변 조건에서 BCC 구조에 속합니다. 현재 많은 문헌에서 Ta 단결정이 고압에서 우수한 상 안정성을 나타낸다는 것이 입증되었습니다[1,2,3]. 게다가 Ta는 다른 대부분의 금속보다 높은 주변 압력에서 3269K의 매우 높은 용융 온도를 가지고 있습니다[4]. Ta는 우수한 특성으로 인해 마이크로/나노 전자공학의 확산 장벽, 마모 방지 코팅 및 고온 초합금과 같은 많은 기술 응용 분야에 이상적인 재료입니다.
최근에는 실험[2, 5,6,7]과 이론[8,9,10,11,12,13,14] 분야에서 많은 노력을 기울이고 있다. 고마워. Dewaele et al. [5]는 최대 93GPa의 다이아몬드 앤빌 셀(DAC)에서 Ta의 항복 강도에 대한 압력의 영향을 연구했으며 DAC 실험에서도 BCC 구조가 최대 135GPa까지 안정적으로 유지되었음을 보여주었습니다[2]. 또한 Shigeaki[8]는 DFT를 사용하여 최대 100GPa 및 3000K Ta의 상태 방정식(EOS)을 시뮬레이션했습니다. Wu et al. [9]는 최대 350GPa의 고압에서 Ta의 탄성 및 열역학적 특성을 조사했습니다. 한편, Škoro et al. [6, 7]은 각각 최대 2250 및 2500K의 매우 높은 온도에서 Ta의 항복 강도와 영률을 측정했습니다. Gu et al. [10]은 제1원리법을 사용하여 500GPa까지의 입방 Ta의 고압 구조 및 탄성 특성에 대한 연구를 수행했습니다. 압력의 함수로서의 탄성 상수와 Ta의 부피, 영 및 전단 계수는 모두 압력이 증가함에 따라 증가함을 알 수 있습니다.
DAC 실험 및 DFT 계산 외에도 MD 시뮬레이션 분야에서 고온 및 고압에 대한 많은 연구가 있습니다[15,16,17,18]. Liu et al. [15]는 확장된 Finnis-Sinclair(EFS) 전위를 사용하고 열 EOS와 최대 400GPa의 압력에서 Ta의 용융 특성을 조사했습니다. 게다가 Tramontina et al. [16, 17]은 고압에서 가소성 메커니즘에 대한 결정 방향의 영향을 연구했습니다. 그들은 또한 충격 강도와 충격 상승 시간이 미세 구조에 미치는 영향에 대해 논의했습니다. 또한, Ruestes et al. [18]은 세 가지 다른 원자 간 전위를 사용하여 BCC Ta에 대한 압입 시뮬레이션을 수행하고 소성 변형 영역의 생성 및 확장을 담당하는 결함 메커니즘을 제시했습니다.
위의 수많은 조사에도 불구하고 MD 시뮬레이션을 사용한 인장 하중 하에서 Ta의 동적 응답에 대한 체계적인 원자 시뮬레이션 연구는 없었습니다. 본 연구의 주요 목적은 크기, 변형률, 온도 및 압력의 영향을 고려하여 <100> 인장 하중 하에서 Ta 단결정의 탄성 특성을 조사하는 것입니다. 또한, <100> 인장하중을 통해 상전이를 유도할 수 있는지 여부를 이해하는 것도 이 작업의 또 다른 목적입니다.
<001>, <010>, <100> 방향을 따라 BCC 단위 셀을 반복하여 본 논문에서 조사한 Ta 입방체를 생성하고 격자 매개변수는 a =b =ㄷ =3.301 Å, 각각. 12a를 포함하여 모서리 길이가 다른 4가지 입방체 모델 (3.96nm), 18a (5.94nm), 24a (7.92nm) 및 30a (9.90 nm), 구성됩니다. 대응하는 원자의 수는 각각 3456, 11,664, 27,648 및 54,000입니다. 그림 1은 가장자리 길이가 3.96nm인 Ta 입방체의 스케치 맵을 보여줍니다. 이는 현재 시뮬레이션의 원래 구조입니다.
<그림><그림><소스 유형="이미지/webp" srcset="//media.springerature.com/lw685/springer-static/image/art%3A10.1186%2Fs11671-018-2526-1/MediaObjects/ 11671_2018_2526_Fig1_HTML.png?as=webp">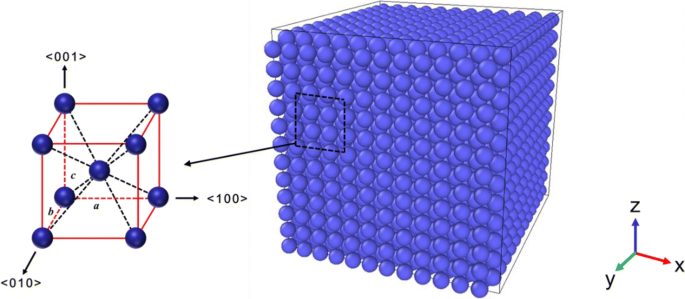
가장자리 길이가 3.96nm인 Ta 입방체의 BCC 구조 및 스케치 맵. 스케치 맵은 현재 시뮬레이션의 원래 구조입니다.
본 논문에서 보고된 MD 시뮬레이션은 대규모 원자/분자 대량 병렬 시뮬레이터(LAMMPS)를 사용하여 수행됩니다[19]. MD 시뮬레이션 과정에서 Ta 원자에 가해지는 외력은 원자 사이의 원자 간 전위 함수에 따라 계산됩니다. 이 연구에서는 두 가지 다른 원자간 전위가 고려됩니다. Zhou et al.의 EAM 전위. [20] 및 Ravelo et al. [21] 각각. 두 전위 모두 표 1에 나열된 Ta의 일부 탄성 속성을 재현하는 데 적용되었습니다. 간단하게 하기 위해 Ravelo-EAM 및 Zhou-EAM 전위라고 합니다.
<그림>3차 대칭 구조의 탄성 거동은 탄성 상수 C로 완전히 설명됩니다. 11 , C 12 , 및 C 44 . <100>, <110> 및 <111> 단결정에 대한 배향 종속 탄성 계수는 여러 방정식을 사용하여 계산됩니다[18]. 우리 작업에서 MD 시뮬레이션은 <100> 인장 하중 하에서 탄성 계수에 대한 영향을 연구하기 위해 수행됩니다. 따라서 <100> 방향에 대한 탄성 계수에 초점을 맞추고 E의 탄성 계수를 취합니다. 100 계정에. 결과적으로, 우리는 탄성 상수 C를 고려합니다. 11 및 C 12 다음 등식[22]:
$$ {E}_{100}=\frac{\left({C}_{11}-{C}_{12}\right)\left({C}_{11}+2{C}_ {12}\right)}{\left({C}_{11}+{C}_{12}\right)} $$ (1)일반적으로 MD로부터 탄성상수를 계산하는 방법은 응력변동법, 변형률변동법, 직접법 3가지가 있다. 현재 작업에서 Gao et al.의 방법과 유사한 직접 방법. [23]은 탄성 상수 C를 계산하는 데 사용됩니다. 11 및 C 12 그림 2와 같이 두 가지 유형의 EAM 전위에 대해.
<그림><그림><소스 유형="이미지/webp" srcset="//media.springerature.com/lw685/springer-static/image/art%3A10.1186%2Fs11671-018-2526-1/MediaObjects/ 11671_2018_2526_Fig2_HTML.png?as=webp">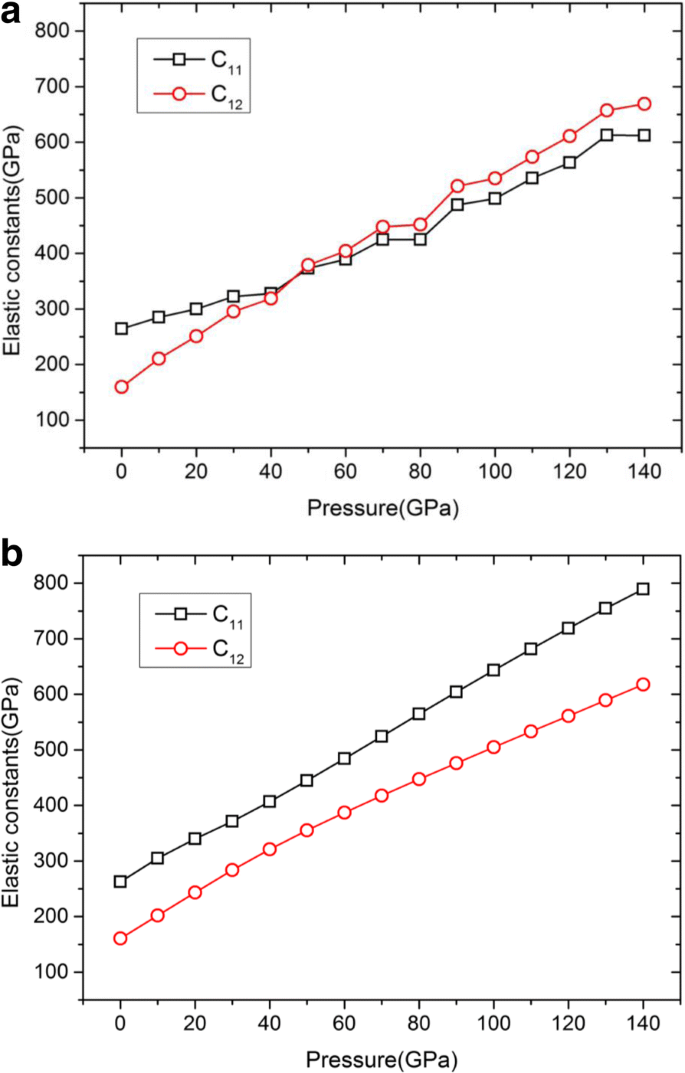
C의 탄성 상수의 압력 의존성 11 및 C 12 연구된 잠재력을 기반으로 합니다. 아 저우-EAM. ㄴ 라벨로-EAM. 현재 작업에서는 직접 방법을 사용하여 탄성 상수 C를 계산했습니다. 11 및 C 12 두 가지 유형의 EAM 잠재력에 대해. 두 전위에 대한 C11/C12-압력 곡선은 a에 나와 있습니다. 그리고 b , 각각
그림 2a에서 두 C 11 및 C 12 Zhou-EAM 잠재력에 기반하여 최대 140GPa까지 증가하는 압력으로 원활하게 진행할 수 없습니다. ~ 40GPa의 압력에서 교차점이 있습니다. 즉, C 11 =C 12 , 여기서 E의 탄성 계수 100 식에 따라 0이 됩니다. (1). 또한 E 100 40GPa 이상의 압력은 음수 값을 제시하며, 이는 의심스럽고 이론 및 실험 결과와 상충됩니다[24, 25]. 따라서 Zhou-EAM 잠재력은 여기에서 고려되는 범위에서 제대로 수행되지 않습니다. 그런 다음 C의 MD 시뮬레이션 결과에서 Ravelo-EAM 전위의 타당성을 검토해 보겠습니다. 11 및 C 12 그림 2b에 표시된 Ravelo-EAM 전위를 기반으로 합니다. 수치 결과는 압력이 높을수록 C 11 및 C 12 , 이는 DFT 계산을 통해 압력에 따라 변화하는 탄성 상수의 경향과 잘 일치합니다[9, 25]. 한편, Ravelo-EAM 전위를 이용하여 계산한 결과는 Ruestes et al.에서 보고한 값과 동일하게 괄목할 만하다. [18]. Ravelo-EAM 전위는 고압에서 잘 작동하며 동시에 동적 변형에서 Ta의 탄성 및 기계적 특성을 설명할 수도 있습니다[26]. 따라서 다음 섹션에서 Ravelo-EAM 잠재력을 기반으로 시뮬레이션을 수행합니다.
기하학적 구성 후 일련의 관련 MD 시뮬레이션을 수행합니다. MD 시뮬레이션 동안 3차원 모델의 세 방향 모두에서 주기적 경계 조건(PBC)이 사용됩니다. 시간 단계는 1fs로 설정되고 시스템 온도는 1, 300, 600, 900, 1200, 1500K로 설정되어 Ta의 탄성 속성의 온도 의존성을 탐색합니다. 먼저 시스템이 로컬 전위 최소값에 놓이도록 정규 앙상블(NVT) MD 시뮬레이션을 사용하여 모델을 약 50ps 이완 프로세스로 완화합니다. 그런 다음 Ta의 탄성 특성에 대한 압력의 영향을 연구하기 위해 0~140GPa 범위의 지정된 정수압을 보장하기 위해 등온-등압(NPT) MD 시뮬레이션을 사용했습니다[27]. 마지막으로 변형률이 5 × 10 8 인 인장 하중 s − 1 ~ 7.5 × 10 9 s − 1 [28, 29]는 Ta 입방체의 x 방향으로 적용됩니다. 한편, NPT 시뮬레이션은 두 번째 단계에서 가해진 동일한 압력에서 y 및 z 방향으로 수행됩니다. 따라서 여기서 계산된 탄성계수는 <100> 방향에 대한 것입니다. 모든 MD 시뮬레이션의 경우, 모델은 <100> 인장 하중
을 통해 x 방향으로 15%의 연신율로 늘어납니다.스트레칭 과정에서 시뮬레이션된 구성은 과학 소프트웨어 패키지 OVITO(Open Visualization Tool)를 사용하여 시각화됩니다[30]. 0 압력에서 <100> 단축 인장 변형률 하에서 Ta의 응력-변형률 곡선과 서로 다른 변형률을 갖는 해당 원자 구성이 그림 3에 나와 있습니다.
<그림><그림><소스 유형="이미지/webp" srcset="//media.springerature.com/lw685/springer-static/image/art%3A10.1186%2Fs11671-018-2526-1/MediaObjects/ 11671_2018_2526_Fig3_HTML.png?as=webp">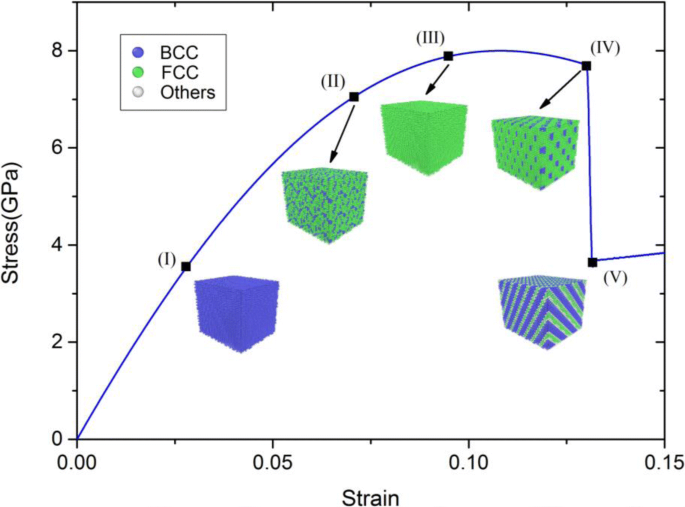
압력이 0일 때 Ta의 응력-변형률 곡선과 변형률이 다른 해당 구성. 참고:파란색, 녹색 및 흰색 공은 각각 BCC, FCC 및 기타 격자 구조에 해당합니다.
그림 3과 같이 응력-변형률 곡선에서 구성(IV) 부근에서 표면이 파단된다는 결론을 내릴 수 있습니다. 단축 인장 변형이 시작될 때 응력은 일반적으로 변형에 따라 선형으로 변하며 그림 3I는 원자 구성이 BCC 구조를 유지함을 보여줍니다. 변형률이 증가함에 따라 BCC에서 FCC 구조로의 상 전이는 각각 그림 3II, II에 표시된 것처럼 ~ .4%의 변형률에서 시작하여 ~ 9.8%의 변형률에서 완료됩니다. 그리고 이러한 FCC 구조는 첫 번째 표면 파단 전에 최대값을 유지합니다. 변형률이 ~ 13.1%일 때 y 및 z 방향의 모서리 길이가 급격히 감소하여 표면 파괴가 발생합니다. 한편, 클러스터는 그림 3IV와 같이 매우 짧은 시간에 발생한다는 점에 주목할 만하다. 연속적인 단축 변형에서 원자 구성은 변형률이 ~ 13.3%가 될 때까지 줄무늬 모양을 유지하며, 이는 그림 3V에 나와 있습니다.
이 문서에서 우리는 이 섹션에서 논의된 모델 크기, 변형률 속도, 온도 및 압력에 대한 인장 속성의 의존성에 집중합니다. 이론적으로 모델은 탄성 변형 단계에서 선형으로 늘어나고 탄성 계수는 응력-변형률 곡선의 선형 부분의 기울기로 정의됩니다. 모든 모델이 유사한 스트레칭 과정을 가지고 있으며 응력-변형률 곡선은 유사한 변화 경향을 가지고 있음을 알 수 있습니다. 따라서 다양한 모델 크기와 변형률 속도의 Ta의 탄성 계수를 얻기 위해 동일한 접근 방식을 사용합니다.
표 2는 1K의 온도와 5 × 10 8 의 변형률에서 다양한 모델 크기의 탄성 계수와 항복 응력을 나열합니다. s − 1 . 모델 크기는 Ta의 탄성 계수와 항복 응력에 영향을 미치지 않는다는 결론을 쉽게 내릴 수 있습니다. 이것은 탄성률이 원자 간의 상호작용을 설명하기 위한 것이며 탄성률은 모델 크기에 따라 달라지지 않는다는 것을 설명하기 매우 쉽습니다. 표 2에서 탄성계수가 ~ 139GPa임을 알 수 있으며, 이는 140GPa의 시뮬레이션 결과와 현저히 동일합니다[18].
<그림>기존 Refs에 따르면. [28, 29], 대부분의 변형률 범위는 10 8 입니다. s − 1 ~ 10 10 s − 1 . 이 논문에서는 인장 시뮬레이션을 수행하기 위해 5.0 × 10 8 을 포함한 네 가지 변형률을 선택했습니다. s − 1 , 7.5 × 10 8 s − 1 , 5.0 × 10 9 s − 1 및 7.5 × 10 9 s − 1 . 표 3은 300K의 온도와 다양한 변형률에서 탄성 계수와 항복 응력을 보여줍니다. 변형률은 탄성 계수와 항복 응력에 명백한 영향을 미치지 않는다는 결론을 쉽게 내릴 수 있습니다.
<그림>한편, 다른 온도 및 압력에서 탄성 계수 및 항복 응력에 대한 모델 크기 및 변형률 속도의 영향도 시뮬레이션합니다. 이러한 시뮬레이션은 동일한 결론에 도달합니다. 따라서 3.96nm의 동일한 모델 크기와 5 × 10 8 의 동일한 변형률을 사용합니다. s − 1 다음 시뮬레이션을 위한 것입니다.
그림 4는 최대 1500K의 다양한 온도에서 응력-변형률 곡선을 보여줍니다. 이러한 곡선의 기울기는 <100> 방향, 즉 E의 탄성 계수를 나타냅니다. 100 , 탄성 인장 기간 동안 항복 응력은 온도가 증가함에 따라 점차적으로 감소합니다. 열역학 이론[31]에 따르면 시스템의 모든 원자의 총 운동 에너지는 일반적으로 다음 방정식을 충족합니다.
$$ {E}_{\mathrm{k}}=\sum \limits_{i=1}^N\frac{1}{2}{mv_i}^2=\frac{3}{2}{Nk} _BT $$ (2)여기서 E k 는 시스템의 총 운동 에너지입니다. 아니 원자의 총 수입니다. 케이 나 볼츠만 상수입니다. 티 열역학적 온도이다. 따라서 시스템은 온도가 높을수록 더 큰 총 운동 에너지를 포함하고 원자가 더 빠르게 움직인다고 결론지을 수 있습니다. 열역학적 관점에서 볼 때 원자는 더 활성화되고 원자의 운동은 더 집중적이며 이는 평형 위치에서 더 큰 진폭을 의미합니다. 스트레칭 과정에서 원자 사이의 인력은 상대적으로 감소하고 원자는 평형 위치에서 쉽게 빠져나가므로 동일한 변형률에서 x 방향의 응력이 감소합니다. 따라서 고온에서의 탄성 계수는 저온에서의 탄성 계수보다 작습니다. 또한 이러한 곡선의 경향은 Ta의 초기 이론 및 실험 결과와 잘 일치합니다[6, 7, 32].
<그림><그림><소스 유형="이미지/webp" srcset="//media.springerature.com/lw685/springer-static/image/art%3A10.1186%2Fs11671-018-2526-1/MediaObjects/ 11671_2018_2526_Fig4_HTML.png?as=webp">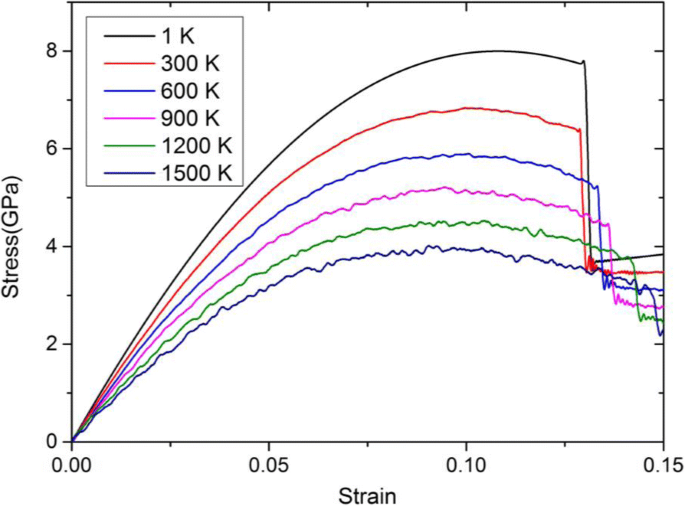
변형률 5 × 10 8 에서 3.96nm Ta 모델의 응력-변형률 곡선 s − 1 및 1에서 1500K의 다양한 온도. <100> 방향, 즉 E에서의 탄성 계수를 나타내는 이러한 곡선의 기울기는 그림 4에서 알 수 있습니다. 100 , 탄성 인장 기간 동안 항복 응력은 온도가 증가함에 따라 점차 감소합니다.
관찰을 용이하게 하기 위해 표 4에는 다양한 온도에서 Ta의 탄성 계수와 항복 응력이 나열되어 있습니다. 탄성 계수는 136.49에서 76.67GPa로 ~ 42.3% 감소하고 온도가 1에서 1500K로 증가함에 따라 항복 응력은 ~ 8에서 ~ 4 GPa로 ~ 51% 감소합니다.
<그림>표 4에 따르면 탄성 계수(E 100 ) 결과는 그림 5a에 실선으로 표시됩니다. 매개변수화는 다음과 같습니다.
$$ {E}_{100}=a+{b}^{\ast }T $$ (3)여기서 E 100 (GPa) 및 T에 있음 (K ); 아 =138.07 ± 0.92111 및 b =− 0.04094 ± 0.00101. 이 방정식은 E 100 온도가 증가함에 따라 선형적으로 감소하며 0 ~ 1500K의 온도까지 사용하는 것이 좋습니다. Eq. (3) E 100 T의 온도에서 0GPa에 도달합니다. 중요 =−아 /나 =3372 K는 Ta의 용융 온도에 매우 가깝습니다[15].
<그림><그림><소스 유형="이미지/webp" srcset="//media.springerature.com/lw685/springer-static/image/art%3A10.1186%2Fs11671-018-2526-1/MediaObjects/ 11671_2018_2526_Fig5_HTML.png?as=webp">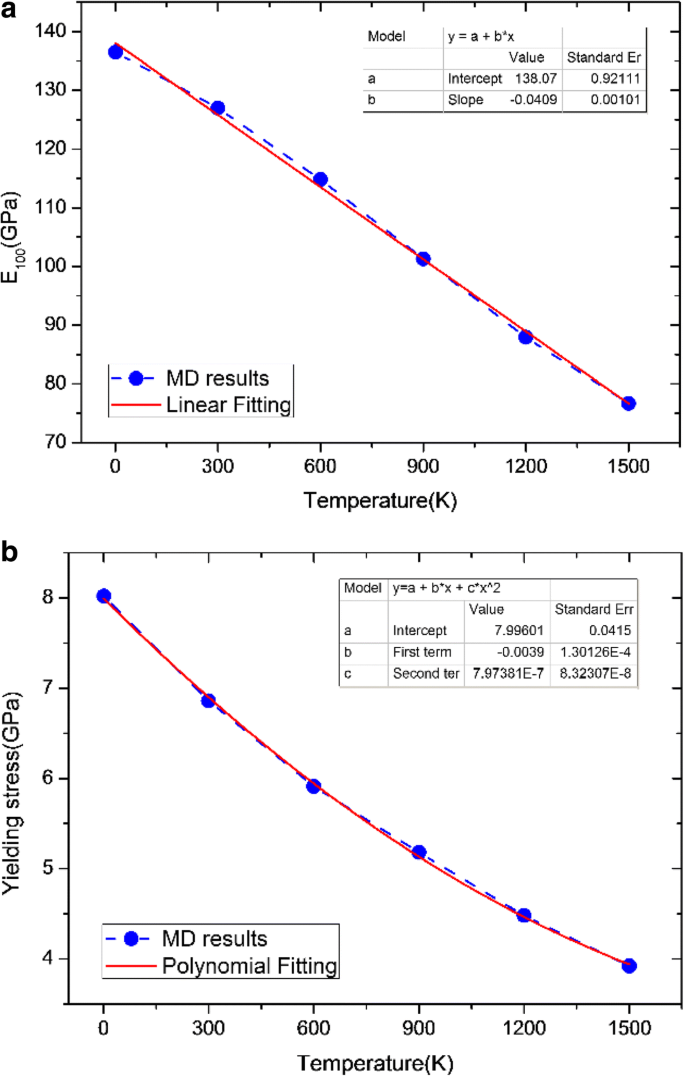
아 탄성 계수 및 b Ta에 대한 항복 응력 대 온도. 그림 5에서 탄성 계수(E 100 ) 결과
항복 응력의 경우 권장되는 매개변수화는 다음과 같습니다.
$$ {Y}_{\mathrm{스트레스}}=a+{b}^{\ast }T+{c}^{\ast }{T}^2 $$ (4)여기서 Y 스트레스 (GPa) 및 T에 있음 (K ); 아 =7.99610 ± 0.0415, b =− 0.0039 ± 1.30126 × 10 − 4 , 및 c =7.97381 × 10 − 7 ± 8.32307 × 10 − 8 . 식에서 (4) 그림 5b의 실선과 같이 이차 다항식 모델을 따르는 온도에 따라 항복 응력이 감소할 가능성이 있음을 알 수 있습니다.
"서론" 섹션에서 언급했듯이 고압 조건에서 Ta의 열탄성 특성에 대한 광범위한 이론 및 실험적 노력이 이루어졌습니다. 정적 방법과 달리 <100> 인장 하중을 통한 동적 방법을 채택하여 E의 탄성 계수의 압력 의존성을 조사합니다. 100 다른 정수압에서.
그림 6은 E의 탄성계수 곡선을 보여줍니다. 100 1~1500K의 서로 다른 온도에서 최대 140GPa의 압력 대. 서로 다른 색상의 모든 실선은 서로 다른 온도에서 동적 방법을 통해 얻은 반면, 정사각형 마커가 있는 점선은 Eq를 사용하여 정적 방법을 통해 얻습니다. (1) C 값 기반 11 및 C 12 0K에서. 1K에서의 곡선, 즉 빨간색 실선에 동그라미 표시가 있는 것이 정적 방법(점선)을 통해 얻은 곡선과 거의 겹치고 있음을 알 수 있습니다. 작업은 최대 140GPa의 고압에서 적용 가능합니다.
<그림><그림><소스 유형="이미지/webp" srcset="//media.springerature.com/lw685/springer-static/image/art%3A10.1186%2Fs11671-018-2526-1/MediaObjects/ 11671_2018_2526_Fig6_HTML.png?as=webp">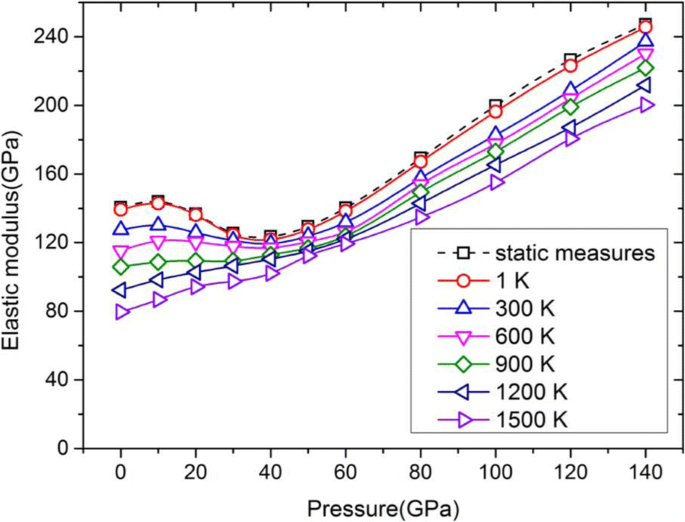
다양한 온도와 압력에서 Ta의 <100> 방향 탄성 계수. 이 곡선의 탄성 계수는 E입니다. 100
그림 6과 같이 E의 탄성계수는 100 600K 이하의 온도에서 압력이 20에서 60GPa로 증가함에 따라 아래쪽으로 오목한 부분이 나타납니다. Ruestes et al. [18]은 MD 시뮬레이션을 사용하여 최대 60GPa의 압력 함수로 탄성 상수를 보고했으며 결과는 계산된 C와 잘 일치합니다. 11 및 C 12 현재 작업에서. 그 대가로 E의 계산된 탄성 계수 100 또한 우리의 결과와 동일한 경향을 보여줍니다. 그러나 E의 계산된 탄성 계수 100 DFT 계산[33]으로부터 압력이 증가함에 따라 점진적으로 증가하고 곡선에서 아래쪽으로 오목한 부분이 발견되지 않습니다. 이러한 불일치가 발생하는 이유는 무엇입니까? 일반적으로 MD 시뮬레이션에 사용되는 전위는 DFT 계산과 실험 결과를 피팅하여 얻습니다. 이러한 의미에서 DFT 계산은 MD 방법보다 정확도가 높습니다. Ravelo-EAM 전위[21]는 Ta 단결정의 피팅 DFT 상태 방정식(EOS) 곡선에 고압 특성을 도입하여 구성됩니다. 피팅 절차 동안 EOS의 콜드 곡선은 격자 상수의 고차(3차 및 4차) 항을 포함하도록 확장되어 MD EOS는 고차 격자 상수 항에 매우 민감합니다. 즉, 이러한 불일치는 Ravelo-EAM 전위가 20~60GPa의 압력에서 Ta의 EOS를 정확하게 설명할 수 없기 때문일 수 있습니다. 전반적으로, 탄성 계수 대 압력의 곡선은 다른 온도에서 유사한 경향을 가지며 탄성 계수는 ~ 40GPa 이상의 압력이 증가함에 따라 점진적으로 증가한다는 결론을 내릴 수 있습니다.
본 논문에서는 <100> 인장하중을 통한 Ta 단결정의 탄성 특성의 온도 및 압력 의존성을 조사하기 위해 MD 시뮬레이션을 수행하였다. 처음에는 Zhou-EAM 및 Ravelo-EAM을 포함한 두 가지 유형의 EAM 전위에 대해 0K 및 다양한 정수압에서 Ta의 탄성 특성 측면에서 비교 연구를 수행했습니다. 결과는 Ravelo-EAM 전위가 다른 압력에서 Zhou-EAM 전위보다 더 잘 작동함을 보여줍니다. 그런 다음 Ravelo-EAM 전위를 기반으로 Ta 단결정의 인장 거동에 대한 MD 시뮬레이션을 수행합니다. 관찰 결과 Ta는 <100> 인장 하중 하에서 파괴되기 전에 BCC-FCC 상전이를 경험하고 모델 크기와 변형률 속도는 Ta 단결정의 인장 거동에 명백한 영향을 미치지 않음을 보여줍니다. 또한, E의 탄성 계수 100 온도가 1에서 1500K로 증가함에 따라 ~ 136에서 ~ 79 GPa로 선형적으로 감소하고 온도가 증가함에 따라 항복 응력이 ~ 8에서 ~ 4 GPa로 감소하여 이차 다항식 공식을 따릅니다. 마지막으로 탄성 특성의 압력 의존성은 0에서 140GPa까지 수행되며 관찰 결과 전체적으로 압력이 증가함에 따라 탄성 계수가 증가함을 보여줍니다. MD 시뮬레이션의 결과는 또한 Ravelo-EAM 전위가 더 높은 압력과 E 계산 공식에서 잘 작동함을 보여줍니다. 100 C 사용 11 및 C 12 140GPa보다 낮은 압력에서.
체심 입방체
다이아몬드 모루 세포
밀도 함수 이론
임베디드 원자 방법
확장된 Finnis-Sinclair
상태 방정식
면 중심 입방체
대규모 원자/분자 대량 병렬 시뮬레이터
분자 역학
등온-등압 앙상블
정규 앙상블
시각화 도구 열기
주기적인 경계 조건
탄탈륨
나노물질
초록 sp2의 육각 네트워크에 대한 결함 -하이브리드화된 탄소 원자는 그래핀 시스템의 고유한 특성에 상당한 영향을 미치는 것으로 입증되었습니다. 이 논문에서 우리는 vacancy uniformity의 결정 하에 이온 C+ 충격에 의해 유도된 결함 있는 단층에서 소수층으로 유도된 결함 있는 단층 그래핀에서 78 ~ 318 K의 저온에서 G 피크 및 D 밴드의 온도 의존적 라만 스펙트럼에 대한 연구를 제시했습니다. 결함으로 인해 G 피크의 음의 온도 계수가 증가하여 D 밴드와 거의 동일한 값을 나타냅니다. 그러나 레이어 번호에 따
초록 이 논문에서는 열 및 진동 보조제가 결합된 하이브리드 가공 공정 중 절단 메커니즘을 조사하기 위해 분자 역학 시뮬레이션을 수행합니다. 하나의 진동 주기에서 재료 제거 거동과 표면 아래 손상 형성을 연구하기 위해 수정된 절단 모델이 적용되었습니다. 결과는 하이브리드 가공 공정 동안 지배적인 재료 제거 메커니즘이 단일 진동 주기에서 압출에서 전단으로 변환될 수 있음을 나타냅니다. 절단 온도가 증가함에 따라 크랙의 발생 및 전파가 효과적으로 억제되고 지배적인 재료 제거 메커니즘이 전단될 때 팽창이 나타납니다. 하나의 진동 주기에서
