나노물질








변형 공학은 물질의 전자 구조를 조정하는 효과적인 방법 중 하나가 되었으며, 분자 접합에 도입되어 고유한 물리적 효과를 유도할 수 있습니다. 변형 제어가 있는 금(Au) 전극 사이에 내장된 다양한 γ-그래핀 나노리본(γ-GYNR)이 설계되었으며, 밀도 기능 이론을 사용하여 스핀 종속 수송 특성의 계산이 포함됩니다. 계산된 결과는 변형의 존재가 분자 접합의 수송 특성에 큰 영향을 미치며, 이는 γ-GYNR과 Au 전극 사이의 결합을 분명히 향상시킬 수 있음을 보여줍니다. 우리는 변형된 나노접합을 통해 흐르는 전류가 변형되지 않은 것보다 더 크다는 것을 발견했습니다. 또한, γ-GYNR의 길이와 변형된 형태는 분자 접합의 수송 특성에 영향을 미치는 중요한 요소로 작용합니다. 동시에 나노접합에 변형을 도입한 후 스핀 분할 현상이 발생하여 변형 공학이 전자 스핀을 조절하는 새로운 수단이 될 수 있음을 시사합니다. 우리의 작업은 미래에 고성능 그래핀 기반 기기를 설계하기 위한 이론적 기반을 제공할 수 있습니다.
전하와 스핀은 전자의 두 가지 주요 고유 속성입니다[1,2,3]. 전통적인 마이크로 전자공학은 종종 전자의 스핀 상태에 관계없이 전자의 전하 특성에 집중합니다. 그리고 전기장[4, 5]을 도입하여 반도체 물질의 전자 수송을 조절하여 정보 수송 또는 처리를 실현하는 것이 일반적인 방법이 되었습니다. 과학 기술의 지속적인 발전으로 대형 집적 회로의 실험이 이전보다 점점 더 많아지고 있습니다[6]. 전자 및 소형화의 고밀도 부품이 시급한 요구 사항이 되었습니다. 최근 수십 년 동안 과학자들은 전자의 스핀 특성을 스핀트로닉스의 분자 장치로 탐구하기 시작했습니다[7, 8]. 스핀의 이완 시간은 상대적으로 길어 스핀 소자의 결함 및 불순물에 쉽게 영향을 받지 않으며 전기장, 자기장 등과 같은 일련의 수단에 의해 달성될 수 있다[9]. 따라서 분자 접합의 스핀트로닉 특성과 관련하여 많은 변조 방법이 집중 연구의 초점이 되었습니다.
화학적 도핑[10,11,12] 및 전자기장 제어[13,14]와 비교하여 변형 공학[15,16,17]은 나노 물질에 대한 가장 효과적이고 제어 가능한 기술로 간주됩니다. 격자와 전자 사이의 상호작용(스핀, 궤도 등. ) 변형 공학에 의해 유도된 재료의 전기적, 자기적 또는 광학적 특성에 영향을 미치며, 이는 다른 고유한 물리적 또는 화학적 효과의 출현으로 이어질 수 있습니다[18, 19]. 또한, 실험 시료 준비 과정에서 불가피하게 변형이 발생하며, 이는 다른 채널에서 적용될 수 있습니다. 예를 들어, 기판이 원활하게 준비되지 않거나[20], 샘플과 기판 재료의 격자 매개변수가 일치하지 않거나[21], 크림프가 나노리본의 가장자리에 존재[22]하는 등입니다.
또한, 변형률은 2차원(2D) 재료의 전자 구조에 명백한 영향을 미치는 것으로 보고되었습니다[23, 24]. 일축 변형이 가해지면 그래핀의 Dirac-cone의 이동이 관찰될 수 있습니다[25]. 그리고 큰 범위의 일축 변형은 그래핀의 제로 밴드 갭을 변경할 수 있습니다[26]. 또한, 최근 연구에서는 변형 공학이 여전히 실리콘 나노와이어의 수송 특성을 개선하는 효율적인 방법임을 보여주었습니다[27]. 흑색 인 나노리본의 단일 층에 변형을 가하는 것은 또한 캐리어의 이동 방향을 변경할 수 있으며, 이는 캐리어 이동성의 이방성을 제어할 수 있다[28]. 또한 변형률은 반도체의 스핀 특성에 영향을 줄 수 있습니다. 밸리 분극 전류는 상승된 기포 구조에 대한 변형을 추가함으로써 그래핀에서 생성될 수 있다[29]. 변형 유도 밴드 수렴은 포스포렌의 열전 성능을 향상시키는 효과적인 방법이 될 수 있다[30]. 또한, 나노접합의 광학적 특성[31] 및 자기적 특성[32]도 변형에 의해 유도 및 변조될 수 있습니다. 따라서 재료에 대한 스트레인 엔지니어링의 규제가 중요하다고 보는 것은 어렵지 않습니다.
최근 몇 년 동안 탄소 과학은 분자 접합의 개발 분야에 널리 영향을 미쳤습니다[33,34,35,36]. 교차 결합 반응을 사용하여 Li et al. [37]은 구리 표면에 graphdiyne 샘플을 성공적으로 합성했습니다. 그 이후로, graphdiyne은 국제 연구자들로부터 큰 관심을 끌었다[38, 39]. 그래핀은 벤젠 고리와 C-C 결합이 아세틸렌 결합과 결합하여 형성되는 2D 평면 네트워크 구조[14, 40,41,42,43,44,45]를 가진 그래핀의 동소체입니다. 단순 레이어드 sp와 비교 2 그래핀의 궤도 하이브리드 구조[46], 그래핀은 sp를 보유합니다. 및 sp 2 혼성화된 상태로, 그것의 독특한 분자 구조가 더 복잡하다는 것을 결정합니다. α-graphyne[40, 41], β-graphyne[47], γ-graphyne[42, 48, 49], α-2-graphyne[14], 6 등 그래핀 계열에 속하는 많은 기존 구성원이 있습니다. 6,12-그래핀[43], 14,14,14-그래핀[44], δ-그래핀[45] 등. 이러한 기존 구조 중 γ-그래핀은 그래핀과 상당히 다른 페르미 준위 주변에서 디랙 원뿔형 전자 구조를 갖지 않습니다. 그래핀 나노리본과 유사하게 γ-그래핀은 안락의자와 지그재그 γ-그래핀 나노리본(AγGYN 및 ZγGYN)으로 절단될 수도 있습니다. 스핀 필터링, 음의 차 저항과 같은 우수한 성능을 관찰하기 위해 ZγGYN에 대한 광범위한 작업이 전시되었습니다. 그러나 금 전극 사이의 ZγGYN에 적용된 변형률에 대한 연구는 보고되지 않았습니다.
ZγGYN에 대한 스트레인 엔지니어링의 장점을 탐구하기 위해 동기를 부여받아 ZγGYN을 기반으로 하는 분자 접합부에 스트레인을 도입하여 첫 번째 원칙 계산을 사용하여 연구를 수행합니다. 이 논문에서 우리는 먼저 서로 다른 자기 구성 내에서 ZγGYN의 전자 구조에 집중했습니다. 관찰 결과, 접합부에 변형률을 도입한 후 스핀 분할 현상이 발생하는 것으로 나타났으며, 이는 변형률이 스핀을 조작하는 수단일 수 있음을 의미합니다. 또한 접합부의 스핀 전류에 대한 결과는 변형률이 어느 정도 소자의 수송 특성에 중요한 영향을 미친다는 것을 의미합니다. 그리고 우리는 변형 공학이 전극과 중간 산란 영역 사이의 결합을 향상시켜 전자 채널을 넓힐 수 있음을 발견했습니다.
그림 1에서 세 가지 다른 분자 접합이 각각 M1, M2 및 M3으로 표시되었습니다. 접합은 왼쪽 전극, 산란 영역 및 오른쪽 전극의 세 부분으로 나눌 수 있습니다. 여기에서는 우수한 연성과 전기 전도성으로 인해 금(Au) 나노 와이어를 전극 재료로 사용합니다. Au 전극은 (111) 표면에서 쪼개져 있습니다. 그리고 산란 영역은 여러 개의 반복되는 ZγGYN 단위로 구성됩니다. 납의 Au 원자와 중앙부의 탄소(C) 원자는 황 원자로 연결되어 있다. 그래핀 접합에 대한 실험에서 그래핀 나노리본은 투과전자현미경(TEM) 내부의 에너지 전자 조사를 사용하여 실험에서 분자 소자로서 맞춤화되고 많은 구조로 절단될 수 있음을 보여주었다[50]. 그래핀과 유사하게 ZγGYN 기반 분자 소자도 이런 방식으로 연결될 수 있습니다. M1은 변형이 도입되지 않고 산란 영역은 그림 1a와 같이 평평합니다. M2는 x U 축 - 그림 1b에서 더 이상 평평하지 않게 만드는 곡선 구조는 가로 변형으로 인해 발생합니다. 구조가 가장 복잡한 M3 시스템의 경우 S -곡선 구조. M3의 산란 영역에서 ZγGYN의 원래 길이는 M1의 것보다 2배 더 큽니다. 따라서 변형 효과가 있는 ZγGYN은 + x의 반대 방향으로 구부러질 수 있습니다. 및 − x 축, S 표시 -그림 1c의 곡선 구조. 그림 1e, f의 M1–M3 측면도는 그림 1a–c의 산란 부분에 대한 주요 보기와 일치합니다. 자세한 교차점은 다음 사진에서 볼 수 있습니다.
<그림>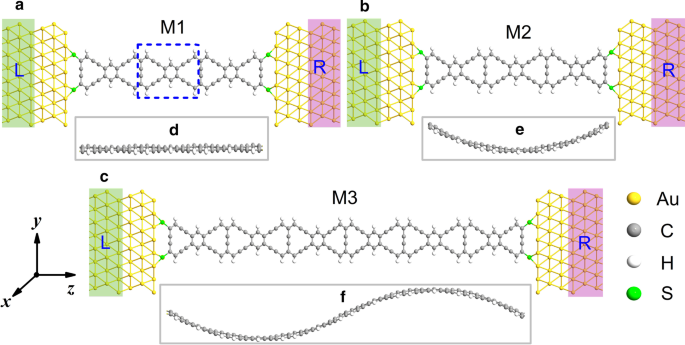
(Color online) 분자 접합 모델의 개략도가 a로 표시되었습니다. M1, b M2 및 c 산란 영역이 평평한 M3, 곡선형(U자형) 및 이중 곡선형(S자형)입니다. 패널 a의 파란색 점선 직사각형 격자 상수가 12.297Å인 ZγGYNR의 반복 단위 셀을 기부합니다. 명확성을 위해 d에 대한 산란 영역의 측면도 M1, e M2 및 f a에 해당하는 M3 –ㄷ 도 전시되었습니다. L/R은 왼쪽/오른쪽 전극을 나타냅니다.
먼저 Atomistix ToolKit 패키지에서 밀도 함수 이론 계산을 구현하여 설계된 단위 셀과 분자 구조를 최적화합니다[51, 52]. 최적화 결과에 따르면 단위 셀의 격자 상수는 그림 1a에서 약 12.297Å이고, M1-M3에 대한 산란 영역의 길이는 그림 1a-c에서 약 36.891Å, 35.473Å 및 70.559Å입니다. 금과 황 원자 사이의 결합 길이는 2.38Å이고 황과 탄소 원자 사이의 결합 길이는 M1-M3의 경우 각각 1.84Å, 1.62Å 및 1.92Å입니다. 자세한 계산 매개변수는 다음과 같이 설정되었습니다. 교환 보정 전위는 함수의 Perdew-Burke-Ernzerh를 사용한 일반화된 기울기 근사로 사용됩니다[53]. 정전기 전위에 대한 메쉬 차단 에너지는 150Ry이고 페르미 함수의 온도는 300K로 설정됩니다. 각 원자에 가해지는 힘은 0.02eV/Å보다 작습니다. 또한 1 × 1 × 100의 Monkhorst-Pack mesh를 선택하고 전자밀도의 수렴기준은 10 −5 총 에너지의 eV. 또한 주기적 이미지 간의 상호작용을 피하기 위해 최소 20Å의 진공층 두께가 계산에 설정됩니다. 에너지의 함수로서의 투과 스펙트럼(E ) 및 바이어스 전압(V )는 다음과 같이 정의됩니다.
$$T_{\sigma } (E,V_{{\text{b}}} ) =Tr\left[ {\Gamma_{{\text{L}}} \left( E \right)G_{\sigma } ^{{\text{R}}} \left( E \right)\Gamma_{{\text{R}}} (E)G_{\sigma }^{{\text{A}}} (E)} \오른쪽],$$여기서 \(G^{{{\text{R}}({\text{A}})}}\)는 중앙 산란 영역의 지연(고급) Green 함수, \(\Gamma_{{\text{ L(R)}}}\)는 왼쪽(오른쪽) 전극과 σ의 결합 행렬입니다. =± 1은 전자 스핀 업/다운을 제공합니다. 스핀 수송 전류는 Landauer-Büttiker 공식을 사용하여 계산됩니다[54, 55]
$$I_{\sigma } \left( {V_{{\text{b}}} } \right) =\frac{e}{h}\int {T_{\sigma } \left( {E,V_{ {\text{b}}} } \right)} \left[ {f_{L} \left( {E - \mu_{{\text{L}}} } \right) - f_{{\text{R }}} \left( {E - \mu_{{\text{R}}} } \right)} \right]{\text{d}}E,$$여기서 \(\mu_{{\text{L(R)}}}\) 및 \(f_{{\text{L(R)}}}\)는 전기화학적 전위 및 왼쪽의 해당하는 페르미 분포 함수입니다. /오른쪽 전극, 각각. 상태의 장치 밀도(DDOS)는 \(D\left( E \right) =- \frac{1}{\pi }{\text{Im}} G^{{\text{R}}로 계산할 수 있습니다. } (E)\).
지그재그 γ-그래핀 단위 셀의 밴드 구조는 각각 그림 2a–c에 표시된 것처럼 비자성(NM), 강자성(FM) 및 반강자성(AFM) 상태로 표시됩니다. 계산 과정에서 위쪽 가장자리와 아래쪽 가장자리에 부착된 탄소 원자의 자기는 모두 같은 방향으로 설정되어 FM 상태에 접근합니다. AFM 상태의 설정은 반대입니다. 에너지 밴드가 그림 2a의 페르미 준위를 통과한다는 점에서 ZγGYNR은 NM 상태에서 금속성임을 알 수 있습니다. NM과 유사하게 FM 상태의 ZγGYNR도 금속이지만 명백한 스핀 분할이 관찰될 수 있습니다. 스핀업 방향의 에너지 밴드는 그림 2b에서 다운시프트된 반면 스핀다운 밴드는 업시프트됩니다. 그러나 ZγGYNR이 AFM 상태로 설정되면 밴드 구조는 0.55eV의 작은 밴드 갭을 나타내어 그림 2c에서 반도체로 만듭니다. 또한 상태의 해당 총 에너지도 M1-M3에 대해 각각 계산되었습니다. 상대적 결과는 다음과 같이 표시됩니다. NM 상태에서 ZγGYNR 단위 셀의 에너지는 -3524.42090eV로 가장 높고 AFM 상태에서 -3524.49299eV로 가장 낮습니다. 가장 높은 에너지와 가장 낮은 에너지 사이의 에너지 차이는 약 0.07eV입니다. 따라서 모든 에너지의 데이터에 따르면 AFM 상태가 ZγGYNR의 기저 상태라는 결론을 도출할 수 있습니다. ZγGYNR의 FM 상태는 나노리본의 스핀 분극을 유도할 수 있으며, 이는 스핀트로닉스 분야에 적용될 것이다. 다음에서는 3개의 교차점에 대한 심층 수송 메커니즘을 설명합니다.
<그림>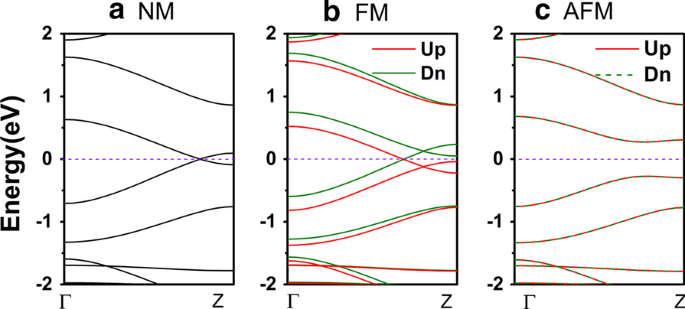
(온라인 색상) ZγGYNR의 밴드 구조는 a 내에 표시됩니다. NM, b FM 및 c AFM은 각각 상태를 나타냅니다. 페르미 준위는 0으로 간주되었습니다.
먼저, 그림 3에 제로 바이어스에서 세 접합의 투과 스펙트럼을 표시합니다. 그림 3a에는 전송 스펙트럼의 급격한 펄스 피크가 많이 있고 페르미 준위 근처에 작은 밴드 갭이 있어 M1이 반도체임을 암시합니다. . 따라서 탄소 원자 사이에 형성된 C=C 또는 C≡C 결합이 전자 수송을 위한 전도 채널을 제공하기 때문에 적절한 전압의 영향으로 전자가 왼쪽에서 오른쪽 전극으로 통과할 수 있습니다. 그림 3b의 M2 변형 장치의 경우 투과 스펙트럼은 M1의 것과 정확히 동일하지 않습니다. 페르미 레벨을 중심으로 이동하는 전송 피크가 여전히 많이 있습니다. 즉, 변형의 영향을 받은 M2의 투과 피크는 M1의 투과 피크보다 넓어집니다. 또한 전송 피크가 모두 페르미 레벨에 가까워지는 것 같습니다. 이 현상은 M2의 산란 영역에 대한 변형의 영향으로 생성되며, 이는 Au 전극과 중간 ZγGYNR 사이의 결합을 향상시켜 전송 채널을 M1보다 더 넓게 만듭니다.
<사진>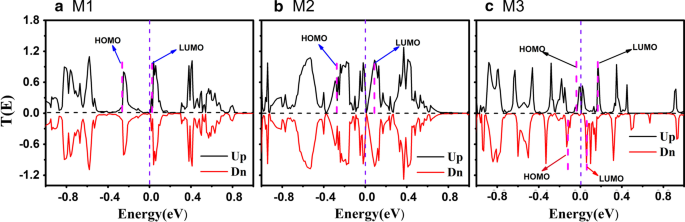
(온라인 색상) 바이어스가 0인 스핀 종속 전송 스펙트럼은 a에 대해 나타납니다. M1, b M2 및 c M3, 각각. 스핀 업 및 다운 전송 계수는 양수(검은색) 및 음수(빨간색) 값으로 설정되었습니다. 한편, 분자 투영 자체 일관성 Hamiltonian의 분포가 여기에 표시되었습니다.
또한 M3의 경우 그림 3c와 같이 스핀업(검은색 실선)과 스핀다운(빨간 실선) 전송 피크가 더 이상 퇴화하지 않는 스핀 분할이 가장 눈에 띄는 특징이다. 더욱이, M3의 투과 피크는 여전히 M1의 그것만큼 날카롭지만, 또한 더 조밀해진다. 스핀 업 전송 피크는 페르미 레벨 앞으로 이동하지만 스핀 다운 전송 스펙트럼은 그림 3c에서 큰 전송 간격을 표시하므로 M3이 스핀 분리된 것처럼 보입니다. 이것은 M3의 S자 모양과 변형 효과의 조합으로 설명할 수 있습니다. S자 모양의 변형은 M3의 전하 분포를 변화시키고 원래의 전기 쌍극자를 파괴하여 M3의 접합부가 자기 거동을 나타내므로 여기에서 스핀 분할 현상을 관찰할 수 있습니다. 분명히, M3의 ZγGYNR은 M1의 두 배이므로 전극과 산란 영역 사이의 상호 작용이 M2보다 약합니다. 그러나 비대칭 S로 인해 -모양 구조, ZγGYNR은 더 이상 동일한 평면에 있지 않으므로 sp를 변경할 수 있습니다. 및 sp 2 γ-graphyne용 하이브리드 구성 요소. 따라서 M3는 새로운 분자 접합을 설계하기에 더 완벽한 모델입니다.
그림 3a, b의 투과 피크의 세부 사항을 주의 깊게 비교함으로써 M1에는 투과 피크가 없고 M2는 -0.02eV의 에너지에서 매우 날카로운 피크를 가지고 있음을 찾는 것이 매우 중요합니다. M1과 M2의 차이점을 깊이 이해하기 위해 그림 4a, b와 같이 0.02eV에서 DLDOS(기기 로컬 밀도)를 그립니다. 그림 4a의 M1의 경우 전자는 주로 금 전극에 국한되어 있고 전자 구름은 ZγGYNR 영역에 덜 분포되어 있습니다. 따라서 M1에 대한 전하 전송을 위한 전송 채널이 더 적습니다. 그러나 M2의 경우 전자가 전체 리본에 걸쳐 전극과 ZγGYNR의 산란 영역에 조밀하게 분포되어 전자 수송을 위해 풍부한 전송 채널이 제공되므로 M2의 전송 스펙트럼이 페르미 준위 주변에서 M1보다 넓어 보입니다. 이 결과는 M2와 변형률 제어의 분자 접합이 더 나은 수송 특성을 유지함을 의미하며 이에 대해서는 나중에 논의합니다.
<그림>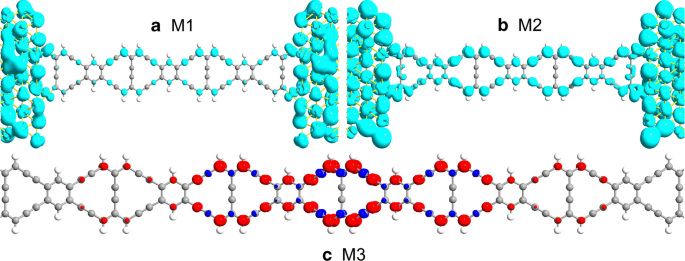
(Color online) 에너지 − 0.02 eV의 DLDOS는 a로 표시되었습니다. M1 및 b M2, 각각. 등가값은 0.01 Å −3 으로 간주됩니다. ·eV −1 . ㄷ M3의 스핀 밀도 등가면도 나타났습니다. 여기서 빨간색과 파란색은 각각 스핀업 및 다운 구성 요소를 나타냅니다. 등가값은 0.015 Å −3 으로 간주됩니다. ·eV −1
또한 각 모델에 해당하는 DDOS가 그림 5a–c에 나와 있으며, 여기서 녹색(주황색) 실선은 각각 스핀업(-다운) 방향을 나타냅니다. 첫째, 그림 5a-c의 DDOS의 모양과 분포는 그림 3a-c와 같은 전송 스펙트럼에 해당합니다. 그림 3a에서 M1의 DDOS는 E에서 급격한 피크를 나타냅니다.> 0이고 스핀업 및 스핀다운 DDOS는 영점에 대해 대칭입니다. 그림 3b의 M2에서 DDOS의 피크는 거의 전체 페르미 준위까지 확장되어 분자 접합의 전하 이동에 기여합니다. 따라서 M2에서 구현된 변형은 페르미 레벨에서 피크 이동을 함께 촉진합니다. DDOS의 피크 구조와 전송 스펙트럼의 유사성은 ZγGYNR의 에너지 준위와 전송 스펙트럼 사이의 명확한 일치를 나타냅니다. 변형으로 인한 Au 전극과 ZγGYNR 간의 결합은 전송 터널을 크게 확장합니다.
<그림>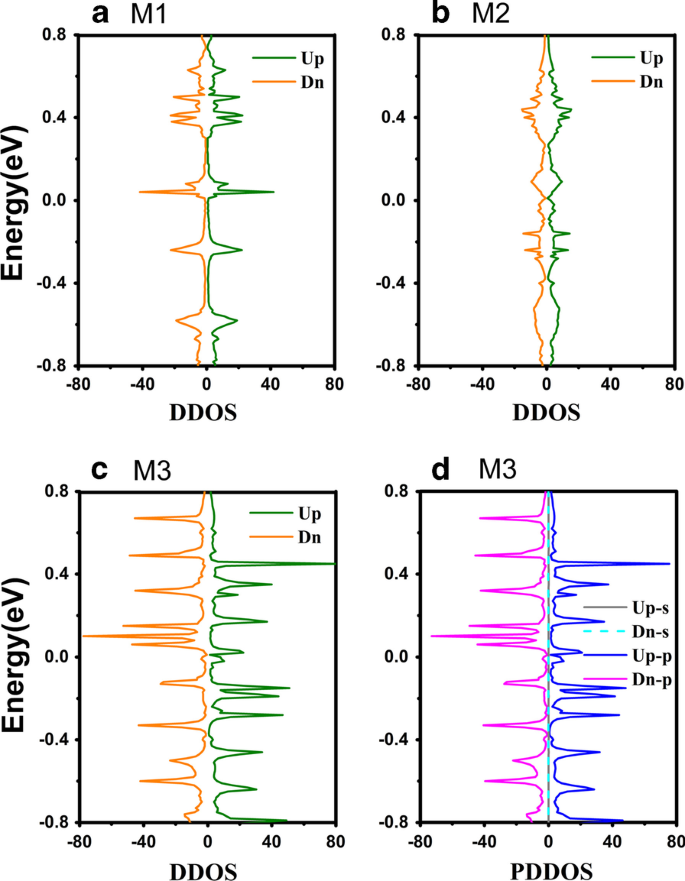
(온라인 컬러) DDOS는 a로 표시됩니다. M1, b M2 및 c M3, 각각. d M3에 대한 PDDOS(계획된 상태 장치 밀도)입니다. "Up-s" 및 "Dn-s"는 s-를 나타냅니다. 스핀 업 및 다운 방향의 궤도 PDDOS, "Up-p" 및 "Dn-p"는 p-를 나타냅니다. 각각 스핀 업 및 다운 방향의 궤도 PDDOS
투과 스펙트럼과 DDOS에서 볼 수 있듯이, M3의 스핀 분할 현상은 그림 5c에서도 관찰할 수 있는데, 이는 ZγGYNR의 긴 분자 사슬을 가진 M3가 자성임을 시사한다. M3의 자성에 대한 직관적인 이해를 돕기 위해 스핀 밀도 분포가 그림 4c에 표시되어 있습니다. 여기서 빨간색과 파란색은 각각 스핀업 및 스핀다운 구성 요소를 나타냅니다. 그림 4c에서 원자 자기 모멘트는 주로 나노리본의 중심에 국한되어 중심에서 가장자리로 갈수록 점차 약해지는 경향을 보이는 것을 알 수 있다. 지그재그 그래핀 나노리본과 유사하게 ZγGYNR은 자성인 것으로 알려져 있다[56]. 그러나 변형의 존재로 인해 전극과 중앙 영역 사이의 결합으로 인해 원래의 자기 분포가 변경됩니다. 따라서 전극에 가장 가까운 원자의 자기는 사라지고 전극에서 가장 먼 중앙 영역의 자기는 남게 된다. 어떤 궤도가 대부분의 자기를 담당하는지 확인하기 위해 그림 5d에 M3의 PDDOS를 표시합니다. PDDOS에서 s- 궤도 전자는 그림 5d의 중간에서 0 값으로 경향이 있기 때문에 M3의 자기에 거의 기여하지 않습니다. 즉, M3의 자기는 주로 p- 피크의 모양과 위치가 모두 그림 5c의 DDOS와 매우 일치하기 때문에 궤도 전자. 따라서 외부 전자의 기여는 M3의 전하 수송에서 내부 전자의 기여보다 훨씬 큽니다. M1-M3의 전송 속성을 표시하기 위해 전류-전압(I-V ) 특성은 다음에서 조사되었습니다. 이전 예측을 확인하기 위해 상대적인 내부 메커니즘이 드러납니다.
모든 시스템에 대해 서로 다른 성능의 해당 메커니즘을 추가로 탐색하기 위해 I–V를 계산합니다. 그림 6a와 같이 제안된 M1–M3에 대한 곡선. 그림 6a는 계산된 스핀 종속 I–V입니다. 각 장치에 적용된 바이어스의 함수로서의 곡선과 삽입물 그림 6a'는 계산된 총 전류를 보여줍니다. 전압 범위가 -0.6에서 0.6V로 증가함에 따라 전류 곡선은 그림 6a와 같이 양의 바이어스 전압 범위와 음의 바이어스 전압 범위에서 대칭적으로 동작합니다. M2 및 M3의 전류는 M1의 전류보다 분명히 더 크며, 이는 변형이 전하 수송에 특정 영향을 미친다는 것을 보여줍니다. 변형이 없는 M1의 전류 크기는 세 접합점 중 가장 작습니다. 바이어스 전압이 증가함에 따라 천천히 증가합니다. 또한 기울기가 가장 큰 M2에 대한 전류는 바이어스 전압이 증가함에 따라 급격히 증가함을 분명히 알 수 있다. 특히, M2의 전류는 동일한 바이어스 전압에서 M1의 전류보다 거의 3배입니다. 대조적으로, S자형 구조의 M3에 대한 전류는 M1과 M2 사이에서 중간이며, 이는 M2보다 약한 전도성 거동을 나타내지만 M1보다 강합니다.
<그림>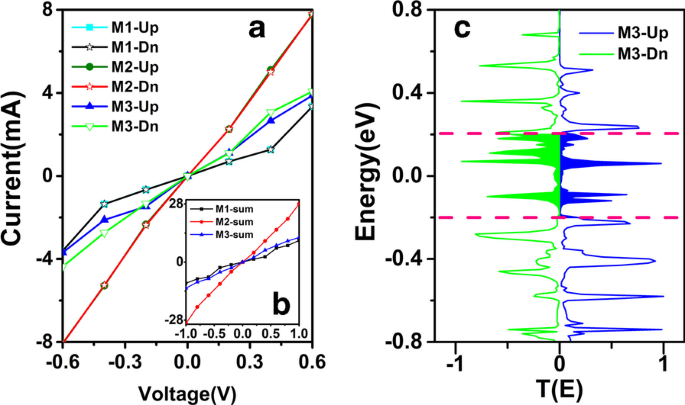
(온라인 색상) a 계산된 스핀 종속 I–V M1, M2 및 M3에 대해 적용된 바이어스의 함수로서의 곡선. 삽입물(a')은 각 장치에 대해 계산된 총 전류를 보여줍니다. ㄴ 바이어스 − 0.04 V에서 M3에 대한 스핀 종속 전송 스펙트럼. 분홍색 점선 사이의 음영 영역은 전류에 기여하는 에너지 영역, 즉 바이어스 창입니다(오른쪽 및 왼쪽의 음영 처리된 파란색 및 녹색 영역은 스핀업 및 스핀다운)
또한 그림 6a의 M3에 대한 전류에서도 스핀 분할 현상을 확인할 수 있습니다. I–V 곡선은 위에서 언급한 투과 스펙트럼 및 DDOS와 매우 일치합니다. 변형이 분자를 더 이상 같은 평면에 있지 않게 하여 비편재화된 접합체 π-를 손상시킨다는 것은 의심의 여지가 없습니다. ZγGYNR의 결합. 그러나 다른 측면에서 고려해야 할 것은 압착 효과로 인해 전극과 산란 영역 사이의 결합이 강화되어 결국 전자 채널이 넓어지고 전류가 증가한다는 것입니다. 따라서 M3의 전류도 변형률의 영향을 받지만 M2의 전류만큼은 아닙니다. 다음과 같은 이유를 설명할 수 있습니다. 산란 영역의 길이는 Au 전극과 ZγGYNR 사이의 결합을 어느 정도 감소시켜 M3의 전류를 M1보다 크고 M2보다 작게 만듭니다. 변형 효과와 ZγGYNR의 길이는 일반적으로 M3의 전류 강도를 결정합니다. 따라서 그림 6a에서 M3에 대해 스핀 종속 전류가 나타나는 것을 볼 수 있습니다. 이는 그림 5c에도 해당합니다. 위의 모든 계산 결과는 변형률이 있는 M3에 스핀 분할 현상이 있음을 보여주지만 실제로는 그다지 중요하지 않습니다. 스핀 변조의 경우 더 효율적인 다른 수단이 있을 수 있습니다. 사실, 전기장[57, 58], 에지 수정[59] 및 도핑[60]과 같은 일부 다른 방법도 많은 2차원 기반 나노 장치에서 스핀 분극을 유도하고 스핀 분할을 향상시킬 수 있습니다. 피>
결과로부터 우리는 M3가 스핀 분할 현상을 가지고 있음을 알고 있으며, 바이어스 전압이 - 0.4 V일 때 스핀 업 및 스핀 다운 전류 값의 차이 |I 위로 – Dn | M3의 경우 가장 큰 것으로 그림 6a의 파란색과 녹색 실선에서 볼 수 있습니다. 이를 위해 그림 6b에 -0.4 바이어스에서 M3의 투과 스펙트럼을 표시합니다. 여기서 파란색 실선과 녹색 실선은 각각 스핀 업 및 스핀 다운 구성 요소를 제공합니다. 바이어스 창에서 녹색 부분의 전송 영역이 파란색 부분의 전송 영역보다 더 큰 것을 볼 수 있습니다. 결과적으로 −0.4V의 동일한 바이어스 전압에서 해당하는 스핀다운 전류가 스핀업 전류보다 큽니다.
그림 3b의 투과 스펙트럼과 관련하여 페르미 준위 근처에서 M2의 투과 피크가 -0.02eV에서 나타나므로 프론티어 분자 오비탈이 전하 수송에 중요한 역할을 한다는 것을 알고 있습니다. 또한, 이전 계산 결과는 M1 및 M2의 전류가 스핀 독립적임을 보여주므로 M1 및 M2에 대한 스핀다운 방향의 MPSH(molecularprojected self-consistent Hamiltonian)의 공간 분포는 여기에서 무시됩니다. 그림 7a의 M1에 대한 가장 높은 점유 분자 궤도(HOMO)의 공간 분포는 그림 7b의 M2에 대한 공간 분포보다 약합니다. M2의 HOMO가 전체 산란 영역에 걸쳐 잘 비편재화되어 M2의 가장 큰 전류가 여기에서 발생함을 알 수 있습니다. M3의 경우 스핀업 HOMO는 그림 7c에서 ZγGYNR의 양면에 분포하는 반면, LUMO(lowest unposed molecular orbital)는 그림 7d에서 주로 중앙 영역에 국한됩니다. 반대로, 변형된 ZγGYNR의 자기 때문에 스핀다운 방향의 HOMO의 파동 함수는 그림 7e의 중앙 영역에 국한되지만 그림 7f의 LUMO 분포는 의 HOMO 분포와 유사합니다. 스핀업 방향. MPSH의 공간 분포는 특정 영역에 상대적으로 국한되어 M3에 대한 더 작은 전류를 나타냅니다. 즉, 분자 오비탈의 상호 작용은 복잡하고 유연한 원자 상호 작용과 외부 효과 간의 조합에 따라 달라집니다.
<그림>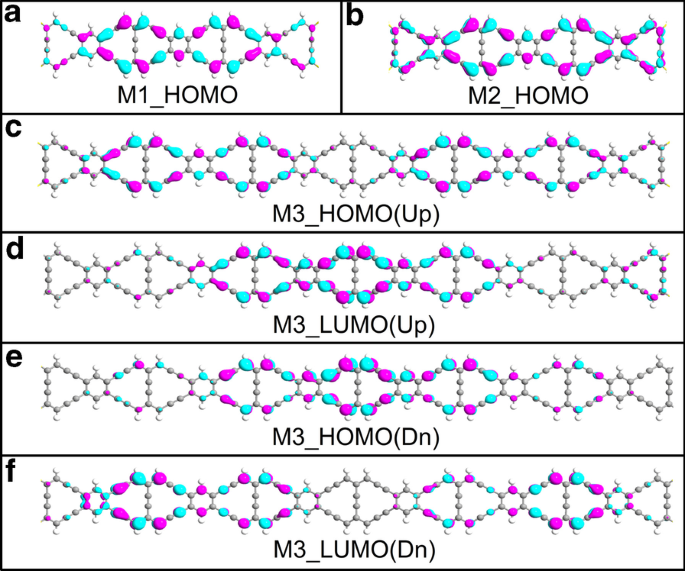
(온라인 컬러) a의 HOMO M1 및 b 스핀업 방향의 M2; ㄷ –f 다른 스핀 방향에서 M3에 대한 HOMO와 LUMO의 공간 분포
요약하면, ZγGYNR을 기반으로 한 변형 접합의 전자 구조와 수송 특성이 연구되고 분석되었습니다. 우리의 결과는 설계된 ZγGYNR의 AFM 상태가 바닥 상태이고 FM 상태의 밴드 구조가 스핀 분할임을 보여줍니다. 또한, 균주는 분자 접합의 수송 특성에 중요한 영향을 미칩니다. 동일한 길이에서 변형은 Au 전극과 ZγGYNR 사이의 궤도 결합을 크게 향상시킵니다. 결과적으로 M2의 전자 채널이 넓어지고 M2의 전자 수송 거동이 M1의 전자 수송 거동보다 훨씬 큽니다. 또한, ZγGYNR의 길이와 방향은 여전히 접합부의 수송 특성에 일정한 영향을 미칩니다. 구체적으로, Au 전극과 ZγGYNR 사이의 결합은 길이의 증가로 인해 약해지기 때문에 M3의 전류는 M2의 전류보다 작다. 또한 M3의 자기 분포는 명백한 스핀 분할 현상을 초래합니다. 전송 특성의 해당 메커니즘은 전송 스펙트럼, LDDOS 등의 측면에서 논의됩니다. 우리의 결과는 앞으로 차세대 플렉서블 전자 장치에 대한 참신한 아이디어를 제공할 수 있습니다.
분자 접합 설계 및 계산 계산은 Atomistix ToolKit 패키지로 수행되었습니다.
γ-그래핀 나노리본
2차원
비자성
강자성
반강자성
상태의 장치 밀도
장치 로컬 상태 밀도
상태의 예상 장치 밀도
분자 투영 자체 일관성 Hamiltonian
가장 높은 점유 분자 궤도
가장 낮은 비어 있는 분자 궤도
스핀업
스핀다운
나노물질
초록 그래핀은 초광대역 광 흡수 및 높은 캐리어 이동성으로 인해 광전자공학 및 광검출 장치에 대한 유망한 재료로 입증되었습니다. 그러나 광전자 시스템과의 통합은 제로 밴드갭과 이득 메커니즘의 부족으로 인해 제한되었습니다. 여기에서 우리는 상당한 밴드갭을 가진 그래핀 나노리본(GRN)을 기반으로 하는 새로운 광검출기를 시연합니다. SiO2 사이의 인터페이스에서 트래핑 전하 활용 및 광 도핑된 실리콘, 22,400의 초고 이득이 얻어졌습니다. 우리 기기는 향상된 광 반응성(~ 800AW−1 ) 응답 속도는 여전히 빠릅니다(최대 10μ
초록 이 연구에서 평균 크기가 3.8 nm인 잘 결정화된 나노 다이아몬드는 펨토초 레이저 절제를 통해 얻습니다. 정상 상태와 일시적인 발광이 모두 관찰됩니다. 나노 다이아몬드의 발광 피크는 여기 파장이 280에서 420 nm로 변할 때 380에서 495 nm로 이동합니다. 폴리에틸렌 글리콜-400N에 의한 패시베이션 후 나노 다이아몬드의 표면이 상당히 산화되었으며 이는 라만 및 UV-Vis 흡수 스펙트럼에 의해 확인됩니다. 또한 최대 강도가 10배 증가하더라도 모든 발광 파장에 변화가 없습니다. 시간 분해 발광 스펙트럼은 트래