나노박스에 대한 마법의 수학 공식

초록

속이 빈 나노구조는 많은 과학적 노력의 최전선에 있습니다. 이들은 나노박스, 나노케이지, 나노프레임 및 나노튜브로 구성됩니다. 우리는 나노박스에서 원자 배위의 수학을 조사합니다. 이러한 구조는 n이 있는 속이 빈 상자로 구성됩니다. 쉘 및 t 외부 레이어. 우리가 유도하는 마법의 공식은 n 그리고 t . t =2 또는 3 또는 몇 개의 레이어만 있는 벽은 일반적으로 대량 배위 원자를 갖습니다. 나노구조에서 낮은 배위의 이점은 벽 두께가 일반적으로 합성되는 것보다 훨씬 얇을 때만 발생하는 것으로 나타났습니다. t =1은 고유하며 고유한 마법 공식이 있습니다. 이러한 저배위 나노박스는 배터리, 연료 전지, 플라즈몬, 촉매 및 생의학 용도를 비롯한 무수히 다양한 응용 분야에 관심이 있습니다. 이러한 공식이 주어지면 나노박스의 표면 분산을 결정할 수 있습니다. 우리는 이 공식이 원자 배위가 n에 따라 어떻게 달라지는지 이해하는 데 유용할 것으로 기대합니다. 그리고 t 나노박스 내에서.

소개

나노박스는 원래 2002년경에 합성되었습니다[1, 2]. 나노박스는 나노케이지가 다공성 벽을 가지고 있다는 점에서 나노케이지와 구별됩니다. 또한, 나노프레임은 클러스터의 저배위 윤곽으로 구성된 구조(frame)라는 점에서 둘 다 나노프레임과 구별된다. 이러한 등방성 다면체 구조는 갈바니 변위 반응에서 생성될 수 있습니다[3, 4]

$$\begin{array}{l}\\ {\hbox{Anode}}:yA_{(s)}\rightarrow yA_{({{\rm aq}})}^{x+}+xye_{({{ \rm aq}})}^{-} \\ {\hbox{음극}}:xB_{({{\rm aq}})}^{y+} + xye_{({{\rm aq}})} ^{-} \rightarrow xB_{(s)} \\ {\hbox{Full\,Reaction}}:yA_{(s)}+xB_{({{\rm aq}})}^{y+} \rightarrow yA_{({{\rm aq}})}^{x+}+xB_{(s)} \\ \end{배열}$$ (1)

여기서 금속 A가 있는 나노클러스터 금속 B 수용액에 의해 희생적으로 속이 비어 있습니다. , 더 높은 환원 가능성을 가지며 요소 B의 속이 빈 솔리드를 생성합니다. . 전기화학 전지의 양극과 음극에서 반쪽 반응이 일어나서 위와 같은 완전 결합 반응이 일어난다[5]. 어떤 경우에는 과학자들이 금속 및 공극의 Kirkendall Fickian 확산을 통한 공극 형성과 갈바닉 변위를 결합했습니다[6]. 이 활동에 대한 모델은 특정 사례에 대해 존재하며 현장 전자 현미경 실험이 보고되었습니다[7, 8]. 다른 합성 방법에는 화학적 에칭[9], 이온 교환[10], 금속-유기 프레임워크(MOF)[11, 12]가 있습니다. 합성 방법에 대한 최근 검토에서는 크기 영역 \(2

이러한 중공 구조는 배위가 낮아 배터리[12], 연료 전지[14], 플라즈몬[15], 촉매[16] 및 생물의학 응용[17]에 대한 관심이 있습니다. 이전 분석에 따르면 촉매 적용의 경우 조정 접근 방식이 적용되는 반면 에너지 저장의 경우 선택 패싯이 중요하다는 DFT(Density Functional Theory) 결과와 함께 일부 힌트만 있습니다[19]. 우리는 인접 행렬 분석[20, 21]에서 이전에 파생된 방법을 사용하여 n이 있는 상자의 원자 배위를 찾습니다. 쉘 및 벽 두께 t 레이어. 이 분석은 t =2 또는 3은 일괄 조정이 있으므로 일반적으로 필요하다고 생각되는 것보다 얇은 벽을 가진 나노박스에만 낮은 조정의 이점이 있습니다. 우리가 사용하는 방법은 13가지 유형의 나노박스에 대한 마법의 숫자와 공식을 통해 원자 배위를 수량화합니다.

방법

조정 방법에 의한 분석의 핵심은 나노박스의 원자 좌표에서 인접 매트릭스를 생성하는 것입니다. 이러한 행렬은 다음과 같이 생성됩니다. 우리는 i를 정의합니다 그리고 j 가장 가까운 이웃으로, 결합 길이 \(r_{ij} $${\mathbf{A}}(i,j)=\left\{ \begin{array}{ll} 1 &{\quad}\hbox { if } r_{ij} 클러스터에 대한 인접 행렬을 설명하고

$${\mathbf{E}}(i,j)=\left\{ \begin{array}{ll} r_{ij} &{\quad}\hbox { if } \, r_{ij} 상자에 대한 유클리드 행렬을 설명합니다. 직경 D를 결정하기 위해 유클리드 행렬을 사용합니다. , (nm) 나노박스.

우리는 가장 가까운 이웃 인접 행렬을 생성하기 때문에 정점 i의 좌표 번호 $\hbox {cn}_i$를 알고 있습니다. ${{\mathbf{A}}}(i,:)$의 요소를 합산합니다. 우리의 구조는 0, 1, ..., n 번호가 매겨진 $n+1$ 셸로 구성됩니다. , t 외부 레이어. $N_{{\rm cn}_i}(n,t)$를 $\hbox {cn}_i$ 배위를 갖는 원자의 수라고 하자. 여기서 $1\le \hbox{cn}_i\le \hbox{cn}_M$과 $\hbox {cn}_M$ 나노박스의 최대 조정. 그러면 나노박스의 총 원자 수는 다음과 같이 표시됩니다.

$$N_T(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{N_{{\rm cn}_i}(n,t)}.$$ (4)

나노박스의 외부 껍질(또는 내부)에 있는 표면 원자, n 벌크 배위보다 적은 결합 세트를 가집니다. 따라서 표면 원자의 최대 배위는 $\hbox {cn}_s <\hbox{cn}_M$이고 표면 원자의 수는

입니다. $$N_S(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_s}{N_{{\rm cn}_i}(n,t)}.$$ (5)

이것은 모든 비표면 정점의 좌표가 $\hbox {cn}_s$보다 큰 경우 적용되며, 이는 모든 fcc, bcc 및 hcp 클러스터에 해당됩니다. 합이 $\hbox {cn}_i$인 인접 행렬의 열을 계산하여 $N_{{\rm cn}_i}(n,t)$를 결정합니다. 클러스터 좌표 알고리즘은 쉘에 의해 구축되므로 각 후속 쉘에는 n의 이전 낮은 값이 모두 포함됩니다. . 또한, 상자에 있는 채권의 수는

$$N_{{\rm B}}(n,t) =\frac{1}{2}\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{\hbox{ cn}_i\cdot N_{{\rm cn}_i}(n,t)},$$ (6)

여기서 $N_{{\rm B}}(n,t)$는 결합 수이고 $\hbox {cn}_M$은 최대 조정입니다. 1/2의 인수는 쌍별 최근접이웃 결합으로 인해 발생합니다.

우리는 이 방정식이 n에 의존한다는 것을 알고 있기 때문에 , 그 최대 3차의 다항식으로 n의 4개 연속 값에 대해 $N_{{\rm cn}_i}(n,t)$를 계산할 수 있습니다. , $n=n_0+j$, j라고 말합니다. =0, 1, 2, 3. 간단한 보간 다항식은 다항식 계수를 제공합니다. 일반적으로 1과 같은 $n_0$을 증가시켜도 공식이 변경되지 않는지 확인해야 합니다. 공식이 $n_0$부터 안정되면 모든 $n\ge n_0$에 대해 유지됩니다. 정확한 유리 계수를 얻으려면 정확한 산술의 계수에 대해 Vandermonde 시스템을 풀어야 합니다.

나노박스에 대한 마법의 공식에는 $n> t$가 있으므로 예상과 달리 t의 적절한 선택으로 상자를 채웁니다. 완전한 고체 클러스터에 대한 원래의 마법 공식을 다시 생성하지 않습니다. 이러한 마법 공식은 클러스터 및 상자 또는 케이지의 중간 규모 속성을 모델링하는 데 유용합니다. 완전한 공식 세트는 원래 19개의 클러스터 유형에 대해 파생되었습니다. 이 원고에서 우리는 13가지 유형의 나노박스에 대한 마법의 공식을 도출합니다.

아래의 마법 공식에서 우리는 t =2 또는 t =셸 두께의 3개 레이어. 대부분은 t 레이어용입니다. =2; 예외는 fcc 정육면체, 정육면체, 정이십면체, bcc 정육면체 및 잘린 정육면체입니다. 후자의 경우 일괄 조정은 t에만 나타납니다. =3개의 레이어. 아래 데이터의 경우 마법 공식 표에는 나노 상자의 내부를 보여주는 '하프 상자' 그림이 함께 표시됩니다. 옆에는 괄호 안의 좌표와 개수를 나타내는 컬러바가 있습니다.

결과 및 토론

마법 공식의 적용 가능성을 설명하기 위해 촉매 거동이 조정 및 그러한 공식에 어떻게 의존하는지 설명합니다. 우리는 G를 정의합니다. 클러스터의 크기에 따른 Gibbs 에너지입니다. adatoms가 외부 껍질 원자에 결합되기 때문에 G가 증가합니다. 이는 흡착 에너지라고 하며 $\Delta G$로 표시됩니다. 이것은 adatoms에 결합하는 외부 껍질에 있는 원자의 다른 배위 유형으로 분할될 수 있습니다. 예를 들어, 꼬임 원자는 $\Delta G_{k}$의 양으로 흡착 에너지에 추가됩니다. 마찬가지로 에지 원자는 $\Delta G_{e}$를 추가하고 패싯 원자는 $\Delta G_f$ 다음 [18]:

에 기여합니다. $$\Delta G=\sum _{o\in \{f,e,k\}} \Delta G_o N_o$$ (7)

여기서 $N_o$는 표시된 유형의 외부 쉘에 있는 원자 수입니다. adatoms에 결합된 외부 껍질의 총 원자 수는 $N_s=N_f+N_e+N_k$로 정의되며, 결과는 다음과 같습니다.

$$\begin{정렬}\Delta G=&{} \Delta G_f\cdot (1-f_e-f_k)+\Delta G_e\cdot f_e+\Delta G_k\cdot f_k \\&\quad {\hbox{where} } \,\,f_o=N_o/N_s, \,\,o\in \{e,k\},\end{정렬}$$ (8)

특정 구조에 대한 명시적인 조정이 있는 가장자리 및 꼬임 사이트를 통해 표현되는 깁스 에너지 분율을 사용합니다. 이것은 마술 공식이 가장자리 및 꼬임 조정과 공식을 통해 표면 반응에 역할을 한다는 것을 보여줍니다. Eq. (8) 상단 부위에 대한 흡착에 적용됩니다. 그렇지 않으면 모든 adatom이 외부 쉘의 원자에 결합되지 않습니다. 이러한 모델에서 꼬임 사이트는 쉘 수 n에 일정한 마법 공식을 갖습니다. , 에지 사이트에는 n과 선형인 공식이 있습니다. , 패싯 사이트에는 n이 있는 이차 공식이 있습니다. . 보다 구체적으로, 꼬임 사이트는 가장 낮은 조정 공식이고, 에지 사이트는 두 번째로 낮은 조정이며, 패싯 사이트는 (100) 패싯의 경우 cn =8, (111) 패싯의 경우 cn =9입니다.

입자별로 두 가지 기본 관계를 적용할 수 있습니다. Gibbs 에너지 및 흡착 상수 $K_{{\rm a}}$에 대해 다음을 유지합니다.

$$K_{{\rm a}}={\exp } \left( -\frac{\Delta G}{RT}\right) ,$$ (9)

여기서 R 는 기체 상수이고 T 켈빈 온도입니다. 또한 Brønsted-Evans-Polanyi 관계는 반응 상수 k에 대한 관계를 사용하여 균질 및 이종 촉매[18, 22]에 널리 사용됩니다. 및 평형 상수 K 다음과 같이:

$$k=gK^{\alpha },\quad 0<\alpha <1,$$ (10)

여기서 g 및 $\alpha$ (Polanyi 매개변수)는 상수입니다. Polanyi 매개변수는 Brønsted[23]가 원래 제공한 대로 단위가 없고 적절한 분수입니다. 그러면 다음과 같은 이점이 있습니다.

$$k=k'_{a}{\exp } \Bigl (-\alpha \bigl ({f_n^{e}\cdot \chi _{_e}({D_n}) +f_n^{k}\cdot \chi _{_k}({D_n})}\bigr )\Bigr ),$$ (11)

어디에

$$\begin{정렬} &\chi _{_e}(D)=\frac{\Delta G_e(D)-\Delta G_f(D)}{RT},\\&\chi _{_k}(D )=\frac{\Delta G_k(D)-\Delta G_f(D)}{RT}, \end{정렬}$$ (12)

그리고

$$k'_{a}=g\exp \left( -\alpha \frac{\Delta G_f}{RT}\right) .$$ (13)

이 분석은 촉매 모델을 결정하기 위해서는 깁스 에너지를 계산하는 방법이 필요하다는 것을 보여줍니다. 2단계 및 Langmuir-Hinshelwood 메커니즘과 같은 알려진 촉매 반응이 고려되었습니다[24].

FCC 나노박스

면심입방 구조는 나노클러스터와 나노박스의 가장 일반적인 형태입니다. 이것은 플라즈몬 특성을 가진 귀금속과 촉매 귀금속과 같은 흥미로운 특성을 가진 금속의 구조입니다. 금은 표준 수소 전극(SHE)[5]에 비해 1.50V의 높은 환원 전위(식 1 참조)를 가지므로 나노박스 또는 나노케이지로 합성하기 가장 쉬운 금속 중 하나입니다. 금 나노박스 또는 나노케이지는 입방체[1], 입방체[25], 정이십면체와 십이면체[26], 팔면체[27] 및 사면체[28] 모양으로 형성되었습니다.

가장 가까운 이웃 결합 길이 r에 대한 조정 접근 방식을 사용하여 이러한 나노박스의 대략적인 크기를 결정할 수 있습니다. (cn) [29],

$$r(cn) =\frac{2r_{{\rm B}}}{\left( 1+\exp \left( \frac{12 - \langle cn \rangle _c)}{8\cdot \langle cn \rangle _c}\right) \right) }.$$ (14)

여기서 $r_{{\rm B}}$는 금(0.2884nm)의 벌크 결합 길이이고 $\langle cn \rangle _c$는 클러스터의 평균 조정입니다. D 사이의 선형 관계를 찾습니다. 그리고 n , 표 1에 표시된 클러스터 셸 수:

$$D(n)=a \cdot r_{{\rm B}} \cdot n + b.$$ (15)

우리는 t와 함께 나노박스를 사용합니다. =3, 공식은 t에 따라 다름 , 그리고 우리는 일부 일괄 조정을 달성하고자 합니다. D 계산을 위해 (n ), 우리는 유클리드 행렬에서 파생된 클러스터의 원자 사이의 최대 거리를 사용합니다. D (n )는 데이터에서 파생된 실험식입니다(n에 따라 다름). D 계산 ), 따라서 입증되지 않았습니다.

이러한 관계는 DFT의 다른 데이터와 일치하는 직경을 생성합니다. N이 있는 정육면체의 경우 55, 561, 923과 같으면 1.12nm, 2.85nm, 3.43nm의 직경을 얻습니다. 이는 1.1nm의 원자 55개[30], 원자 561개의 경우 2.7nm[31], 원자 923개의 경우 3.5nm[30]에 대해 발표된 DFT 결과와 유리하게 비교됩니다. 일부 fcc 나노박스에 대한 마법 공식은 아래 표에 나와 있습니다(표 2, 3, 4, 5, 6, 7, 8).

이십면체 및 십이면체 나노박스

표 9 및 10을 참조하세요.

다이아몬드 및 단순 큐빅 나노박스

다이아몬드 입방 격자 구조는 탄소 동소체와 실리콘 및 게르마늄 원소에 의해 형성됩니다. 또한 일부 입방체 화합물은 입방체 산화철, 사면체 다이아몬드 마그헤마이트 $\gamma$-Fe₂와 같은 구조를 형성합니다. O₃ . 사면체 다이아몬드 마그헤마이트 $\gamma$-Fe₂에서 Fe–O의 결합 길이 O₃ =0.186nm[32]. 이것은 다이아몬드 클러스터 D의 직경으로 이어집니다. (n ) 아래와 같이:

$$D(n) =3.3984\cdot n_{{\rm B}} \cdot n - 0.21194.$$ (16)

참고 문헌 [12]에 따르면 입방체 산화철의 마이크로박스가 형성되었고 흥미로운 리튬 저장 능력이 있었습니다. 우리는 에너지 저장을 위한 완전한 조정 모델을 알지 못하지만 위에서 언급한 바와 같이 DFT 결과는 활동이 패싯 방향에 따라 달라질 수 있음을 나타냅니다[19]. 우리가 촉매에 대해 가지고 있는 것처럼 조정에 대한 저장 의존성의 그러한 모델은 현재 존재하지 않습니다. 위의 방정식 (16)에서 (t를 사용하여 생성됨) =4), 마이크로박스에는 약 n개가 필요합니다. =다이아몬드 마그헤마이트용 껍질 1600개 다이아몬드 및 단순 입방 격자 구조의 마법 공식은 아래에 나열되어 있습니다(표 11, 12).

BCC 나노박스

표 13, 14, 15를 참조하세요.

HCP 나노박스

표 16을 참조하세요.

사례 t =1

특별한 경우 t =1은 고유하므로 고유한 마법 공식이 있습니다. 우리는 위의 나노박스 중 일부에 대해 이 경우를 조사합니다. 초박형 벽을 가진 나노박스는 입방체[33], 팔면체[16] 및 20면체 모양[34]으로 형성되었습니다. 아래의 마법 공식에 따르면 t가 있는 큐빅 나노박스는 =1은 조정이 가장 낮습니다. 백금은 SHE에 비해 1.18V의 상대적으로 높은 환원 전위를 가지므로 갈바닉 대체에 의해 형성될 수 있습니다(Eq. 참조). (1) [5]. 그러나 이러한 백금 기반 나노케이지 중 일부의 산화 환원 반응(ORR) 특성은 (100) 면과 대조적으로 (111) 면을 갖는 구조가 더 나은 ORR 질량 활성을 갖는다는 것을 나타냅니다[35].

따라서 20개(111)개의 면을 가진 20면체가 ORR 질량 활성도가 가장 높고 그 다음이 8면체, 마지막으로 잘린 정육면체입니다. 배위 번호보다 우선하는 패싯 배향에서 촉매 거동의 이러한 속성은 아래 표 데이터에 의해 입증됩니다. 즉, 다음 표에서 언급한 바와 같이 (100)면체를 갖는 큐브는 4 및 5로 가장 낮은 마법 좌표수를 갖지만 (111)면체 및 더 큰 마법 공식을 갖는 팔면체 및 이십면체는 더 나은 ORR 활성을 갖는다. 이 속성은 DFT 결과가 특히 PtNi 합금의 경우 [36] (111) 패싯의 우세를 확인하는 나노클러스터에서도 입증됩니다(표 17, 18, 19, 20, 21).

분산

촉매 활성과 관련하여 패싯 사이트에 비해 가장자리 및 꼬임 사이트의 중요성을 감안할 때 우리는 우리가 연구하는 일부 나노박스에 대한 표면 분산을 결정했습니다. (100) 패싯은 cn =8이고 (111) 패싯은 cn =9입니다. 이것은 나노박스 간에 비교할 때 개별 다면체 활동에 대한 이유에 대한 통찰력을 제공할 수 있습니다. 아래 그림 1에서 표면 분산 $D_{{\rm s}} =(N_{{\rm e}} + N_{{\rm k}}) / N_{{\rm S}} \cdot 100\%$. 이 관계에서 $N_{{\rm k}}$는 꼬임 또는 모서리 사이트의 수이고 $N_{{\rm e}}$ 에지 사이트의 수입니다. 그림 1에서 볼 수 있듯이 (100) 표면이 아닌 (111) 표면이 있는 나노박스는 분산이 더 높아 (111) 면의 촉매 활성이 선호된다는 믿음을 줍니다.

<그림>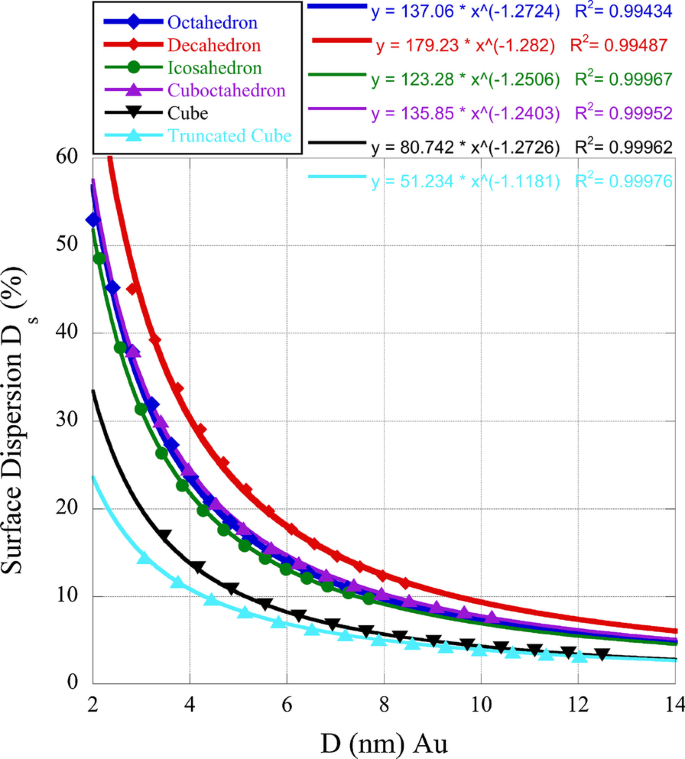

금 나노박스의 표면 분산

결론

요약하면, 우리는 나노박스에 대한 마법 공식에 대한 첫 번째 상세한 수학적 설명을 제시했습니다. 쉘 두께의 경우 t =1은 $t>1$과 다르며 이러한 경우 중 일부에 대한 데이터를 표로 만듭니다. 배위, 원자 수 및 결합 수에 대한 공식이 모두 열거됩니다. t 레이어에 대해 일괄 조정이 나타납니다. =2 또는 3이며 일반적으로 합성되는 것보다 훨씬 얇습니다. 낮은 조정의 이점은 매우 얇은 벽에서만 얻을 수 있습니다. 이러한 결과가 모델링 및 실험 작업에 유용할 것으로 기대합니다.

데이터 및 자료의 가용성

이 기사의 결론을 뒷받침하는 데이터세트는 교신저자로부터 얻을 수 있습니다.

약어

숨은 참조:: 몸 중심 입방체
fcc:: 면심입방체
hcp:: 육각형 밀착 포장
DFT:: 밀도 함수 이론
그녀:: 2차 수소 전극

향상된 약물 전달을 위한 후두암 세포 및 면역 세포 내 고분자 나노입자의 세포 내재화에 대한 정량적 평가 근적외선 강화 나노미터 블랙 실리콘 기반 이중 4사분면 광검출기

나노물질