Tellegen의 정리 – 해결된 예제 및 MATLAB 시뮬레이션

Tellegen의 정리 – 해결된 예가 있는 단계별 가이드

텔레겐의 정리란 무엇입니까?

텔레겐의 정리 네덜란드의 전기 엔지니어이자 발명가인 Bernard D.H. Tellegen이 출판했습니다. 이 정리는 네트워크 분석의 다른 정리 중에서 가장 중요하고 근본적인 정리입니다. 대부분의 다른 정리는 이 정리에서 파생됩니다.

텔레겐의 정리는 키르히호프의 법칙에 따릅니다. 따라서 이 정리는 Kirchhoff의 법칙을 따르는 네트워크에 적용될 수 있습니다. 이 정리는 선형 또는 비선형, 시변 또는 비변이, 수동 또는 능동 요소를 갖는 광범위한 네트워크에 적용할 수 있습니다.

Tellegen의 정리는 다음과 같이 말합니다.

텔레겐의 정리는 에너지 보존 법칙의 원리에 따라 작동합니다. 이 정리는 물리적 네트워크의 동적 동작을 찾기 위해 화학적 및 생물학적 응용 프로그램에서 사용됩니다. 신호 처리에서 이 정리는 필터를 설계하는 데 사용됩니다.

• 관련 포스트:Thevenin의 정리. 해결된 예가 있는 단계별 가이드

수학 방정식

정리의 일반적인 분석을 위해 우리는 네트워크에 'n'개의 요소가 주어졌다고 생각합니다. 요소를 통과하는 순간 전류는 i₁입니다. , 나는₂ , 나는₃ , ...., 나는_n . 그리고 이 분기의 순시 전압은 v₁입니다. , v₂ , v₃ , ...., v_n .

따라서 element-1의 순시 전류와 전압은 i₁입니다. 및 v₁ . 순시 전력(p₁ ) 이 요소에서 소비한 값은 v₁입니다. 나는₁ .

p ₁ =v ₁ 나 ₁

요소-2의 순시력은 (p ₂ );

p ₂ =v ₂ 나 ₂

마찬가지로, n ^번째 의 순시력 요소는 (p _n );

p_n =v_n 나는_n

텔레겐의 정리에 따르면 모든 순간 전력의 합은 0입니다. 모든 순시 전력 p₁을 합산해야 함을 의미합니다. , p₂ , p₃ , ...., p_n .

p ₁ + p ₂ + p ₃ + … + p_n = 0

v ₁ 나 ₁ + v ₂ 나 ₂ + v ₃ 나 ₃ + … + v_n 나는_n  = 0

일반적으로 k ^번째 에 대한 위 방정식을 작성할 수 있습니다. 지점;

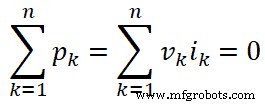
어디서,

• n =네트워크의 총 분기 수
• v_k =k ^번째 의 순시 전압 지점
• i_k =k ^번째 의 순시 전류 지점
• p_k =k ^번째 의 순시 전력 지점

이제 AB 분기가 k 분기와 같으므로 아래 그림을 고려하십시오.

따라서 순시 전압 v_k ;

v_k =v_a – v_b

그리고 분기(a에서 b까지)를 통과하는 순간 전류는 i_k입니다. ;

i_k =i_ab

즉시 전력 p_k 이다;

p_k =v_k 나는_k =(v_a – v_b ) 나는_ab … .. (1)

이제 순시 전류의 반대 방향(b에서 a)을 고려합니다.

i_ab =– i_ab

순시 전압;

v_k =v_b – v_a

순시 전력 p_k 이다;

p_k =v_k 나는_k =(v_b – v_a ) 나는_바 ….. (2)

방정식-1과 2의 합;

2v_k 나는_k =(v_a – v _b ) 나 _ab + (v_b – v_a ) i_ba

v_k 나는_k =1/2 [(v_a – v _b ) 나 _ab + (v_b – v_a ) 나는_바 ] ….. (3)

이 방정식은 n-가지에 대해 아래와 같이 작성할 수 있습니다.

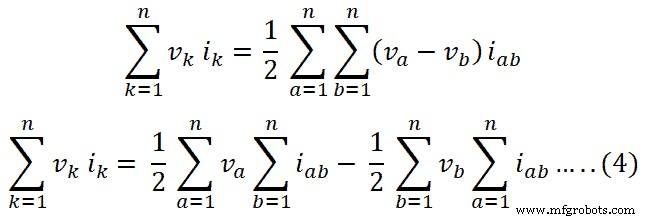
Kirchhoff의 현재 법칙에 따르면 전류의 대수적 합산은 회로의 노드에서 0입니다.

따라서

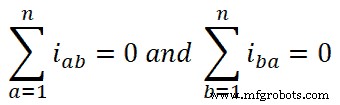
이 값을 방정식-4에 넣으면 다음을 얻습니다.

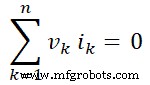
따라서 네트워크에 전달되는 전력의 합이 0임을 증명합니다. 따라서 Tellegen의 정리가 증명되었습니다. 또한 네트워크 요소에 의해 흡수된 전력의 합은 소스에서 전달되는 전력의 합과 같다고 설명됩니다.

• 관련 게시물: Norton의 정리. 해결된 예가 있는 단계별 가이드

텔레겐의 정리를 따라야 할 단계

Telegen의 정리에 의해 전기 네트워크를 해결하려면 아래 단계를 따라야 합니다.

1단계: 주어진 전기 네트워크에서 여러 가지를 찾아야 합니다. 그런 다음 각 분기에서 전력 소산을 찾습니다. 전력을 찾으려면 기존의 분석 방법을 사용하여 해당 분기의 전압 또는 전류를 찾아야 합니다.

2단계: 각 가지의 순간적인 힘을 찾아보세요.

3단계: 전력 공급 분기로 간주되는 에너지 소스가 있는 분기입니다. 그리고 다른 요소를 가지고 있는 가지를 흡력 가지라고 생각합니다. 이제 동력 전달 지점과 동력 흡수 지점을 식별하십시오.

4단계: 전력 공급 분기에서 양의 부호를 가정하고 전력 흡수 분기에서 음의 전압 강하를 가정합니다. 역 신호를 가정할 수도 있습니다. 그러나 예제 전체에서 변경할 수는 없습니다.

5단계: Tellegen의 정리를 정당화하려면 모든 가지에서 계산된 모든 검정력을 더해야 합니다. 그리고 이 합계는 항상 0입니다.

• 관련 게시물:SUPERMESH 회로 분석 – 단계별 해결 예

예를 들어 이해합시다.

Tellegen의 정리 해결 예

예시 #1

아래 네트워크에 대한 Tellegen의 정리를 정당화합니다.

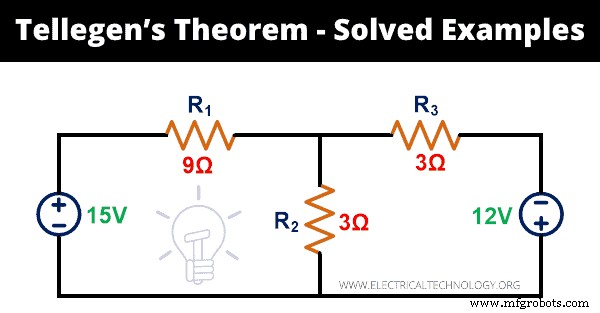
해결책:

1단계: 주어진 회로망에는 5개의 분기가 있습니다. 순시 전력을 계산하려면 각 분기를 통과하는 전류를 찾아야 합니다. 이를 위해 네트워크에 KVL을 적용합니다.

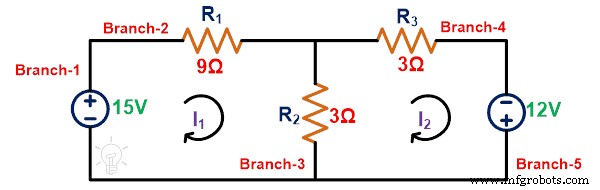
루프-1에 KVL을 적용합니다.

15 =12나 ₁ – 3나 ₂

루프-2에 KVL을 적용합니다.

12 =– 3나 ₂ + 6나 ₂

위의 방정식을 풀면 루프 전류 I₁의 값을 찾을 수 있습니다. 그리고 나₂ . 그리고 이러한 값은;

나 ₁ =2A

나 ₂ =3A

2단계: 분기 3을 통과하는 전류는 다음과 같습니다.

나 _{1 2} =나 ₂ – 나 ₁ =3 – 2 =1A

모든 분기를 통해 흐르는 전류가 있습니다. 이제 각 지점의 힘을 찾아보세요.

P ₁ =V 나 ₁ =15 x 2 =30W

P ₂ =알 ₁ 나 ₁ ² =9 x 4 =36W

P ₃ =알 ₁ 나 ₁₂ ² =3 x 1 =3W

P ₄ =알 ₃ 나 ₂ ² =3 x 9 =27W

P ₅ =V 나 ₂ =12 x 3 =36W

3단계: 소스가 있는 두 분기가 있습니다. 이 가지는 동력을 전달하는 가지이고 나머지 세 가지는 동력을 흡수하는 가지입니다.

여기서 이 예에서는 전력 전달 분기의 부호가 양수이고 전력 흡수 분기의 부호가 음이라고 가정합니다. 따라서 분기 1과 5는 전력을 전달하는 분기이고 다른 분기는 전력을 흡수하는 분기입니다.

4단계: 전력 P₁의 기호 및 P₅ 양수(전력 전달 분기)이고 P₂의 부호입니다. , P₃ , 및 P₄ 음수(전력 흡수 분기)입니다.

5단계: 이제 모든 분기에서 소산되는 전력의 합계를 찾아야 합니다.

P ₁ – 피 ₂ – 피 ₃ – 피 ₄ + 페 ₅ =30W – 36W – 3W – 27W + 36W =0W

따라서 순시 전력의 합은 0입니다. 따라서 이 정리가 증명됩니다.

• 관련 게시물:SUPERNODE 회로 분석 – 단계별 해결 예

예시 #2

텔레젠의 정리를 사용하여 6A 전류 소스의 전압을 구합니다.

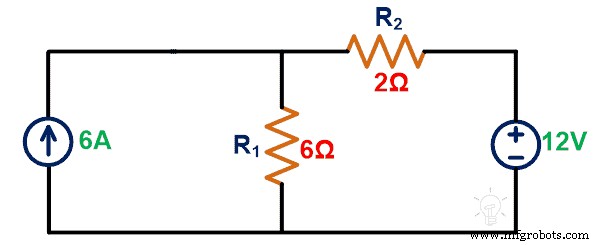
해결책:

1단계: 요소를 통과하는 전압 또는 전류를 계산해야 합니다. 이를 위해 주어진 네트워크에 KCL 또는 KVL을 적용합니다.

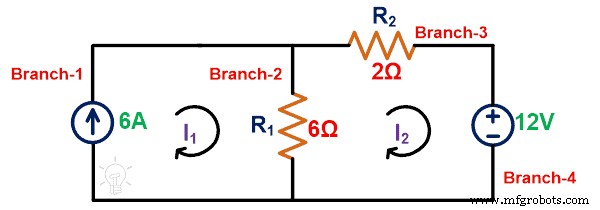
루프-2에 KVL을 적용합니다.

-12 =8나 ₂ – 6나 ₁

현재 소스가 있는 분기를 통과하는 현재 패스는 I입니다. ₁;

나 ₁ =6A

이 값을 위의 방정식에 대입하십시오.

-12 =8나 ₂ – 6(6)

-12 =8나 ₂ – 36

36 – 12 =8나 ₂

24 =8나 ₂

나 ₂ =3A

2단계: 분기-2를 통과하는 전류는 다음과 같습니다.

나 ₁₂ =나 ₁ – 나 ₂ =6 – 3 =3A

이제 각 분기의 힘을 찾아보세요.

P ₁ =V 나 ₁ =V x 6 =6 x V

P ₂ =알 ₁ 나 ₁₂ ² =6 x 9 =54W

P ₄ =알 ₂ 나 ₂ ² =2 x 9 =18W

P ₄ =V 나 ₂ =-12 x 3 =-36W

3단계: 여기에서 에너지원을 가진 두 개의 가지가 있습니다. 그러므로 우리는 이 가지들을 힘을 전달하는 가지라고 생각해야 합니다. 그리고 양의 부호를 순시 전력으로 설정합니다.

저항만 있는 다른 두 가지. 따라서 이 가지는 전력을 흡수하는 가지이며 순시 전력에 음수를 설정합니다.

4단계: 전력 P₁ 및 P₄ 양수 부호와 거듭제곱 P₂ P3에는 음수 부호가 있습니다.

5단계: 이제 모든 순간 전력을 요약해야 합니다.

P ₁ – 피 ₂ – 피 ₃ + 페 ₄ =0W

P ₁ – 54 – 18 + 36 =108W

6A 전류 소스가 제공하는 전력은 108W입니다. 따라서 전류 소스의 전압은 다음과 같이 계산됩니다.

P ₁ =V 나

108W =V x 6A

V =18V

따라서 전류 소스의 전압은 18V입니다.

• 관련 게시물: AC 및 DC 회로의 최대 전력 전달 정리

MATLAB을 사용한 Tellegen의 정리 분석 및 시뮬레이션  

목표:

위의 예에서 주어진 회로도에 대해 Tellegen 정리를 증명하십시오.

요구사항: MATLAB

이론:

텔레겐의 정리에 따르면 모든 분기의 순시 전력 합은 0입니다. 이 정리를 증명하려면 모든 가지의 순시 전력을 계산해야 합니다.

순시 전력을 찾으려면 모든 분기의 전압 또는 전류를 계산해야 합니다. 이를 위해 KCL 또는 KVL 정리를 사용할 수 있습니다. 하지만 여기서는 MATLAB Simulink 모델을 사용하여 전류와 전압을 구합니다.

multisim, psim 등과 같은 다른 소프트웨어도 사용할 수 있습니다. Simulink 모델에서 회로도를 구성하겠습니다. Simulink 모델을 통해 각 분기의 전압과 전류를 찾을 수 있습니다.

그 후에 전압과 전류에서 순시 전력을 찾을 수 있습니다. 일부 소프트웨어에서 순시 전력을 직접 찾을 수 있습니다.

MATLAB Simulink 모델

아래 그림은 위 예의 회로도입니다.

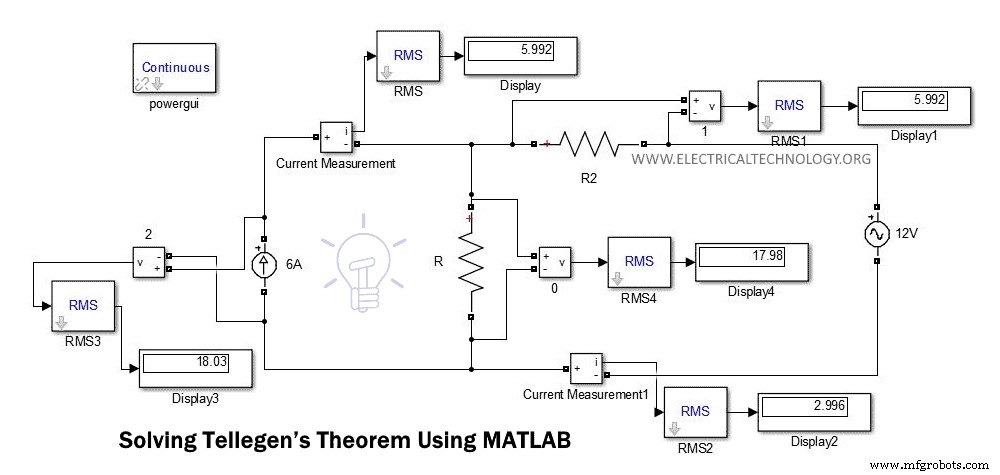
이 그림에서 디스플레이에서 전압과 전류를 직접 찾을 수 있습니다. KCL 또는 KVL을 사용하여 전압과 전류를 계산하여 이 값을 비교할 수 있습니다.

계산

전압 또는 전류를 계산한 후 순시 전력을 구할 수 있습니다. 또는 소프트웨어에서 순간 전력을 직접 찾을 수 있습니다. 우리에게 필요한 것은 순간적인 힘입니다. 그리고 나서 모든 권한을 추가해야 합니다.

힘의 합은 항상 0입니다. 이 예에서는 Simulink에서 찾은 전압 및 전류 값과 이전 예에서 KVL 및 KCL을 사용하여 계산한 동일한 값을 비교합니다. 이 값은 동일합니다.

이 값은 브레드보드의 저항과 소스를 연결하여 계산하기도 합니다. 그리고 전압계와 전류계를 사용하여 모든 분기를 통과하는 전압과 전류를 측정할 수 있습니다.

따라서 Tellegen의 정리가 증명됩니다.

• 관련 포스트:Kirchhoff의 전류 및 전압 법칙(KCL 및 KVL) | 해결 예

텔레겐 정리의 적용

이 정리는 매우 기본적이며 회로 분석에서 널리 사용됩니다. 이 정리의 많은 응용 프로그램이 있습니다. 일부 응용 프로그램은 아래에 나열되어 있습니다.

• 필터를 설계할 때 이 정리는 디지털 신호 처리 응용 프로그램에서 매우 유용합니다.
• 화학 공장의 안정성을 결정하기 위해 이 정리를 화학 공학에서 사용합니다.
• 이 정리는 선형-비선형, 능동-수동, 시변/시불변 요소가 있는 집중 시스템에 적용됩니다.
• 이 정리는 생물학적 과정에서 사용됩니다.
• 구조 반응의 토폴로지 및 분석에 사용됩니다.
• 물리적 네트워크의 동적 동작을 찾는 데도 사용됩니다.

관련 전기 회로 분석 튜토리얼:

• 중첩 정리 – 해결된 예를 통한 회로 분석
• Cramer의 법칙 계산기 – 전기 회로에 대한 2 및 3 방정식 시스템
• 휘트스톤 브리지 – 회로, 작업, 파생 및 응용
• 전기 및 전자 공학 계산기
• 5000개 이상의 전기 및 전자 공학 공식 및 방정식