3D 매달린 구조 제작을 위한 원스텝 마스크 기반 회절 리소그래피

초록

우리는 선폭이 작은 마스크 패턴의 회절을 활용하여 3차원(3D) 매달린 구조를 제작하기 위한 새로운 원스텝 노광 방법을 제안합니다. 노광 공정의 광학 모델을 구축하고 Fresnel-Kirchhoff 회절 공식을 기반으로 포토레지스트의 3D 광 강도 분포를 계산합니다. 빔, 메쉬, 단어 패턴 및 다층 구조와 같은 여러 3D 부유 포토레지스트 구조가 달성되었습니다. SU-8 구조의 열분해 후 부유 및 독립형 3D 탄소 구조가 추가로 얻어지며 투명 전극, 반투명 태양 전지 및 에너지 저장 장치의 응용 분야에서 큰 잠재력을 보여줍니다.

소개

3D 탄소 미세 전자 기계 시스템(C-MEMS) 구조는 우수한 화학적 안정성, 전기화학적 활성 및 생체 적합성으로 인해 점점 더 많은 관심을 받고 있습니다[1,2,3,4,5]. 부유 탄소 구조는 분자간 성질이 없는 전형적인 3D C-MEMS 구조[2]로, 센서[6, 7], 미세전극[8, 9] 및 에너지 저장 응용 분야[9]에서 상당한 이점을 제공합니다. 다양한 C-MEMS 미세구조는 폴리머의 열분해를 통해 달성되었으며, 여기서 SU-8은 열분해 탄소 구조에 가장 널리 사용되는 전구체입니다[10, 11]. 낮은 광 흡수와 관련하여 SU-8 [12]로 높은 종횡비의 미세 구조를 쉽게 제작할 수 있습니다. 그러나 현탁 폴리머 템플릿을 얻는 것은 여전히 큰 도전입니다.

E-beam writer[13,14,15], X-ray[10,16] 및 2광자 리소그래피[17,18,19]와 같은 부유 미세구조를 제작하기 위해 다양한 접근 방식이 개발되었습니다. 2광자 리소그래피는 부유 중공 마이크로튜브와 같은 복잡한 부유 구조를 정확도는 높지만 효율성은 낮추기 위해 실현 가능한 방법입니다[17]. 효율성과 비용을 고려하면 UV 리소그래피가 포토레지스트 전구체 제조에 더 나은 선택이 될 수 있습니다. 매달린 구조를 제작하기 위해 노출량을 제어하는 다단계 리소그래피 공정이 입증되었습니다[3, 6, 7, 20]. Lim et al. [21] 2단계 UV 리소그래피 공정을 사용하여 부유 나노와이어 및 나노메쉬를 제작하고 열분해 공정을 통해 유리질 탄소 나노구조를 얻었다. 일부 원스텝 리소그래피 방법도 제안되었습니다. 없음 외. [22]는 광 확산 필름이 Cr-마스크 위에 놓이는 동안 단일 노출 공정에 의해 부유 미세 구조를 달성했습니다. 디퓨저 필름은 노광 공정에 상당한 영향을 미쳐 포토레지스트 패턴의 변형을 초래했습니다. Long et al. [2] 근접 노광 공정 동안 포토레지스트와 포토마스크 사이의 노광량과 에어 갭을 제어하여 3D 현수 구조를 성공적으로 제작한 반면, 근접 노광 모드는 제작 해상도를 제한했습니다. 그레이스케일 포토리소그래피는 그레이스케일 마스크 또는 마스크 없는 리소그래피 시스템을 사용하여 매달린 구조를 제작하는 데에도 적용되었습니다[11, 23]. SU-8은 빛의 파장이 350 nm 이상일 때 거의 투명하기 때문에[12], 노광량을 조절하여 부유층 두께의 정확도를 제어하는 것은 매우 어렵습니다[8, 10]. Hemanth et al. [10] SU-8의 특성에 따라 노광 공정에서 UV 파장을 최적화하였다. 그들은 높은 비율의 미세구조에 대해 405 nm의 UV 파장을 선택하고 부유층에 대해 313 nm의 UV 파장을 선택했습니다. 그러나 서로 다른 UV 광 파장으로 노출되는 조합은 전체 제조 공정의 비용과 어려움을 증가시킵니다.

이 연구에서 우리는 3D 부유 구조를 제작하기 위해 대부분의 포토레지스트와 호환되는 새로운 원스텝 마스크 기반 회절 리소그래피 공정을 시연합니다. Kirchhoff의 회절 이론에 따라 포토레지스트에서 3D 광도 분포를 시뮬레이션하고 실험을 통해 추가로 검증합니다. 매달린 구조물의 두께는 패턴의 폭에 의해 조절되며, 여러 개의 라인 패턴을 적절한 간격으로 나란히 쌓아서 매달린 빔을 확장합니다. 경사 두께의 빔 및 단어 패턴의 전체 매달린 메쉬와 같은 복잡한 3D 매달린 구조는 원스텝 리소그래피 프로세스로 달성할 수 있습니다. 마지막으로 매달린 탄소 빔, 메쉬 및 독립형 탄소 메쉬도 열분해 공정을 통해 얻었습니다.

방법 및 실험

회절 리소그래피의 광학 모델

UV 리소그래피 공정 중에 패턴 크기가 너무 작으면 회절 현상이 매우 분명해집니다. 여기에서 우리는 여러 파장 폭을 가진 좁은 패턴의 회절을 활용하여 부유 빔을 제작합니다. 포토레지스트의 공간 광 강도 분포를 분석하기 위해 프레넬 회절을 기반으로 하는 회절 리소그래피에 대한 광학 모델(그림 1)을 구축합니다. 하드 콘택 모드에서 노광이 이루어지기 때문에 포토레지스트와 포토 마스크 사이의 에어 갭은 무시할 수 있습니다. 마스크는 365 nm의 일반적인 파장에서 평면파로 조명되고 포토레지스트는 굴절률 1.659(엘립소미터로 측정한 365 nm에서 SU-8의 굴절률)를 갖는 투명 물질로 처리됩니다. 피 ₀ 좌표가 (x인 마스크의 점입니다. ₀ , y ₀ , 0) 및 P ₁ (x 좌표를 갖는 포토레지스트의 임의의 지점) ₁ , y ₁ , z ₁ ).

<그림>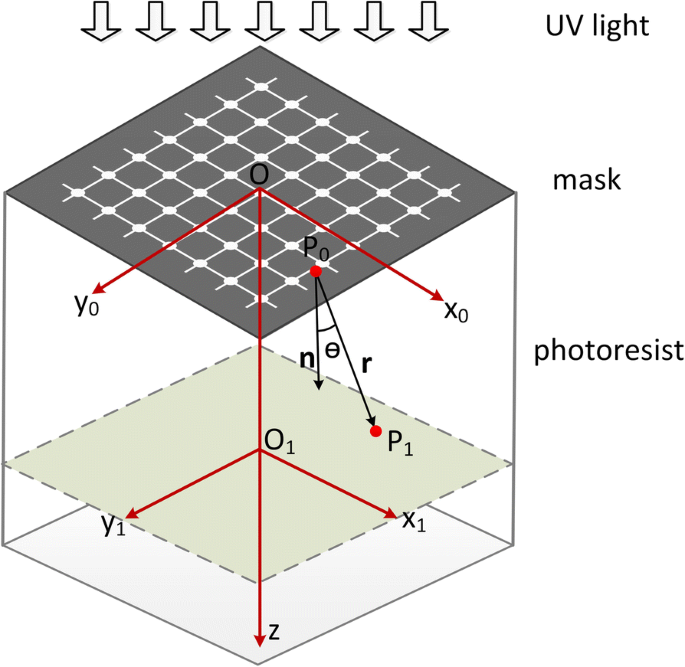

회절 리소그래피의 광학 모델

Fresnel-Kirchhoff 회절 공식[24]에 따르면 점 P에서의 진폭은 ₁ 포토레지스트에서

$$ E\left({P}_1\right)=\frac{1}{2 j\lambda}\underset{\sum }{\iint }E\left({P}_0\right)\frac{\ exp (jkr)}{r}\left(1+\cos\theta\right) ds $$ (1)

여기서 k =2π /λ , λ 포토레지스트의 UV 광 파장을 나타냅니다. E (피 ₀ )는 포인트 P에서의 광파 진폭입니다. ₀ , θ P 사이의 각도입니다. ₀ 피 ₁ 그리고 z 축, r P 사이의 거리입니다. ₁ 그리고 피 ₀ , 및 Σ 마스크 패턴의 적분 영역을 나타냅니다. 그림 1의 기하학적 관계에 따라 다음을 얻을 수 있습니다.

$$ r=\sqrt{{\left({x}_1-{x}_0\right)}^2+{\left({y}_1-{y}_0\right)}^2+{z_1} ^2} $$ (2) $$ \cos \theta ={z}_1/r $$ (3)

이 (피 ₀ )은 모델에서 상수입니다. 따라서 계산 공식은 다음과 같습니다.

$$ E\left({P}_1\right)=\frac{E\left({P}_0\right)}{2 j\lambda}\underset{\sum }{\iint}\frac{\exp \Big( jk\sqrt{{\left({x}_1-{x}_0\right)}^2+{\left({y}_1-{y}_0\right)}^2+{z_1} ^2\큰)}}{\sqrt{{\left({x}_1-{x}_0\right)}^2+{\left({y}_1-{y}_0\right)}^2 +{z_1}^2}}\left(1+\frac{z_1}{\sqrt{{\left({x}_1-{x}_0\right)}^2+{\left({y}_1 -{y}_0\right)}^2+{z_1}^2}}\right){dx}_0{dy}_0 $$ (4)

그런 다음 Matlab 소프트웨어를 사용하여 적분을 계산하고 포토레지스트의 광도 분포는 다음과 같이 표현할 수 있습니다.

$$ I\left(x,y,z\right)={\left|E\left({P}_1\right)\right|}^2 $$ (5)

여기서 (x , y , z )는 P의 좌표와 같습니다. ₁ .

포토레지스트의 흡수를 더 조사하기 위해 흡수 계수를 고려할 때 광도 계산을 수정했습니다. 광선이 P의 포토레지스트를 통과할 때 ₀ 피로 ₁ , 광도는 다음 공식으로 계산할 수 있습니다[25].

$$ \frac{I_{\alpha }}{I_0}=\exp \left(-\alpha r\right) $$ (6)

나 ₀ P 지점에서의 초기 광도 ₀ , 나 _α 포인트 P에서의 광도 ₁ , α 는 포토레지스트의 흡수 계수이며 r P 사이의 거리입니다. ₀ 그리고 피 ₁ . 우리는 나를 정의합니다 _{α = 0} 포인트 P에서의 광도 ₁ α일 때 =0 μm⁻¹ . 나 _{α = 0} =나 ₀ 식 (6)에 따라. E 간의 관계 (피 _{α = 0} ) (I에 해당하는 진폭 _{α = 0} ) 및 E (피 _α ) (I에 해당하는 진폭 _α )는 다음과 같이 표현할 수 있습니다.

$$ \frac{E\left({P}_{\alpha}\right)}{E\left({P}_{\alpha =0}\right)}=\exp \left(-\alpha r /2\오른쪽) $$ (7)

따라서 회절 리소그래피에서 포토레지스트의 흡수를 고려할 때 점 P에서의 진폭은 ₁ (E로 정의됨 (피 _1α ))는 다음과 같이 계산할 수 있습니다.

$$ E\left({P}_{1\alpha}\right)=\frac{1}{2 j\lambda}\underset{\sum }{\iint}\exp \left(-\alpha r/ 2\right)E\left({P}_0\right)\frac{\exp (jkr)}{r}\left(1+\cos\theta\right) ds $$ (8)

그리고 빛의 세기는 식 (2), (3), (5), (8)로 구할 수 있습니다.

실험 세부정보

선 패턴이 있는 마스크는 매달린 구조를 제작하는 데 사용되었으며 원형 또는 사각형은 매달린 층을 지지하는 기둥 제작을 위해 설계되었습니다. 두 종류의 두꺼운 네거티브 포토레지스트가 ~ 50 μm 두께의 SU-8 2100(Microchem Co., Ltd.)과 ~ 30 μm 두께의 NR26-25000P(Futurrex Co., Ltd.)를 포함하여 실험에 사용되었습니다. 노광 공정은 MJB4 마스크 정렬기로 수행되었으며, 여기서 조명 UV 광의 파장은 365 nm였습니다. 샘플을 현상액에 일정 시간 담근 후 매달린 구조를 얻을 수 있습니다. 여기에서 SU-8 2100 샘플의 현상액은 프로필렌 글리콜 메틸 에테르 아세테이트(PGMEA, Aladdin Co., Ltd.)를 사용했으며 NR26-25000P 샘플은 RD6 현상액(Futurrex Co., Ltd.)을 선택했습니다. 마지막으로, 석영로(MTI GAL 1400X)에서 하드 베이킹 단계와 탄화 베이킹 단계를 포함하는 열분해 공정[16, 26, 27]을 수행하여 3D 탄소 미세 구조를 얻었습니다. 전체 공정을 그림 2a에 나타내었고, 열분해 과정 중 온도 변화를 그림 2b에 나타내었다. 샘플을 300°C에서 30분 동안 하드 베이킹한 다음 900°C에서 60분 동안 열분해했습니다. 열분해 과정에서 샘플은 H₂ (5%)/Ar(95%) 분위기, 가열 속도 10 °C/min. 얻어진 미세구조를 주사전자현미경(SEM, Helios NanoLab G3, FEI)으로 특성화하였다.

<그림>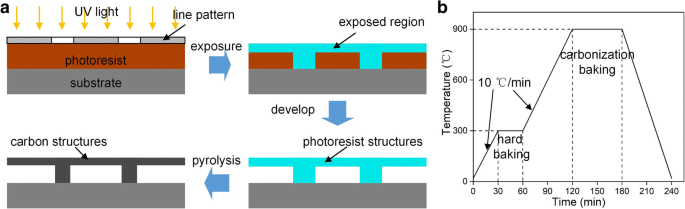

아 3D 탄소 현수 구조물 제작 과정. ㄴ 열분해의 온도 곡선

결과 및 토론

광도 분포

그림 3a는 선 너비가 d인 선 모양 마스크 아래의 3D 광도 분포의 단면을 보여줍니다. =1 μm, 1.5 μm, 2 μm, 2.5 μm, 3 μm, 3.5 μm, 4 μm. 여기서 상대강도를 적용하고 입사광강도를 1로 정의한다. 포토레지스트 바닥의 빛은 빛의 회절효과로 인해 점차적으로 산란된다. 빛의 강도가 임계값에 도달하면 포토레지스트는 반응을 방출하고 고체가 되기에 충분한 에너지를 얻습니다. 그렇지 않으면 개발 프로세스에서 제거됩니다. 임계값(본 연구에서는 0.75) 위 영역의 두께는 패턴 폭에 매우 민감한 노출 깊이로 정의됩니다. 노출 깊이는 d에서 5.3 μm입니다. d에서 =1 μm 및 18.2 μm =2 μm. d에서 33.5 μm로 더 증가합니다. d에서 =3 μm 및 47.5 μm =4 μm. 선폭이 1 μm보다 좁으면 두꺼운 포토레지스트의 요철로 인한 마스크와 포토레지스트 사이의 에어갭이 노광을 실패하게 하기 때문에 노광 깊이가 제조에 너무 작아질 것이다. 그림 3b, c는 매달린 구조를 제작하기 위한 마스크 패턴과 z에서의 해당 광도 분포를 보여줍니다. =5, 10, 15 및 20 μm, 여기서 선 너비는 2 μm로 설정됩니다. 선과 메쉬 패턴의 노출 깊이는 15~20 μm인 반면 큰 정사각형과 원형의 노출 깊이는 리소그래피 중에 기둥을 형성하기에 충분히 큽니다. 따라서 기둥에 의해 지지되는 매달린 빔과 메쉬가 제작될 수 있습니다. 선폭이 5 μm 이상이면 현수구조물 제작이 어렵기 때문에 그림 3d와 같이 선패턴을 나란히 쌓아 넓은 현수보나 메쉬를 제작한다.

<그림>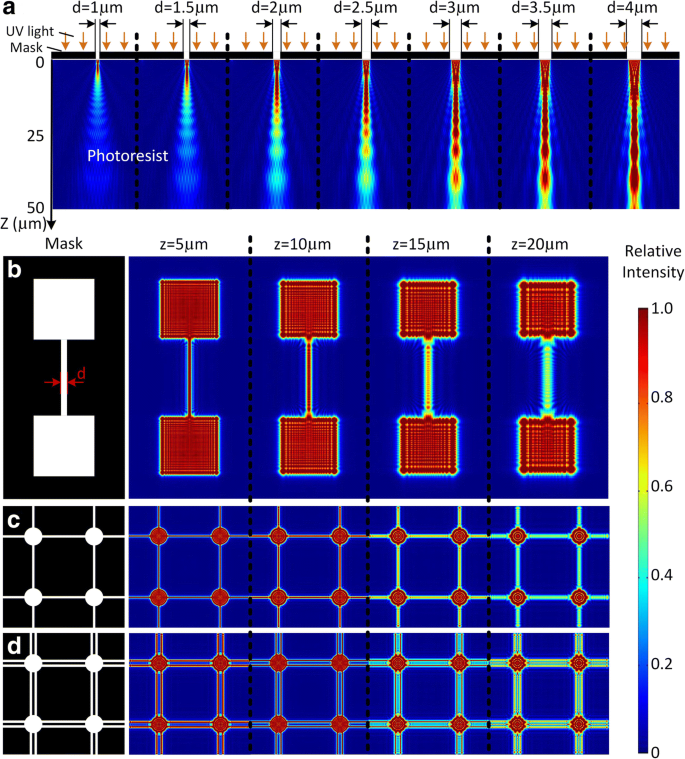

마스크 패턴 및 시뮬레이션 결과 포토레지스트가 생성됩니다. 아 d 아래의 포토 마스크 아래의 광도 분포 =1 μm, 1.5 μm, 2 μm, 2.5 μm, 3 μm, 3.5 μm 및 4 μm, 여기서 d 선 패턴의 너비입니다. b의 마스크 패턴 매달린 빔, c 메쉬 및 d z 아래에 쌓인 선 패턴과 해당하는 광도 분포가 있는 메쉬 =5 μm, 10 μm, 15 μm 및 20 μm 포토레지스트. 여기, z 단면 평면과 포토 마스크 사이의 거리

중단된 포토레지스트 구조

매달린 구조물을 제작하기 위한 실험이 수행되었습니다. 포토레지스트 기둥을 얻기 위해 최소 노출 시간을 테스트하고 이를 노출 임계값으로 정의했습니다. 그런 다음, 시뮬레이션에 따라 임계값의 4~3배를 노광량으로 채택하고 상대 광도 임계값을 0.75로 평가했습니다. 그림 4는 서로 다른 d 아래 매달린 포토레지스트 빔을 보여줍니다. 값. 부유층의 두께 h d와(과) 긍정적인 관련이 있습니다. . NR26-25000P 포토레지스트의 경우 h d에서 10.9 μm입니다. =2 μm(그림 4a) 및 d에서 25.5 μm로 증가 =4 μm(그림 4e). d 5 μm에 도달하면 노출 깊이가 기판에 도달할 만큼 충분히 크며 매달린 구조가 얻어지지 않습니다(그림 4f). 그림 4g–k는 SU-8의 매달린 구조를 보여줍니다. h의 기능 대 d 실험과 시뮬레이션 모두 그림 4l에 나와 있으며, 여기서 직선은 최소 자승법으로 적합합니다. 선형 상관 계수 R 적합선 중 R ² =0.963, 0.988 및 0.858 흡수를 계산하지 않은 시뮬레이션의 경우 각각 NR26-25000P 및 SU-8입니다. SU-8 실험의 결과가 시뮬레이션 결과와 매우 유사함을 알 수 있다. 대조적으로, NR26-25000P의 부유층은 흡수가 없는 시뮬레이션의 부유층보다 훨씬 얇습니다. 이것은 주로 SU-8의 투명 특성과 NR26-25000P의 높은 흡수 능력에 기인합니다. 이것이 또한 회색 노출이 일부 포토레지스트에 대해 매달린 구조를 제작하는 데 사용될 수 있지만 SU-8에는 적합하지 않은 이유이기도 합니다.

<그림>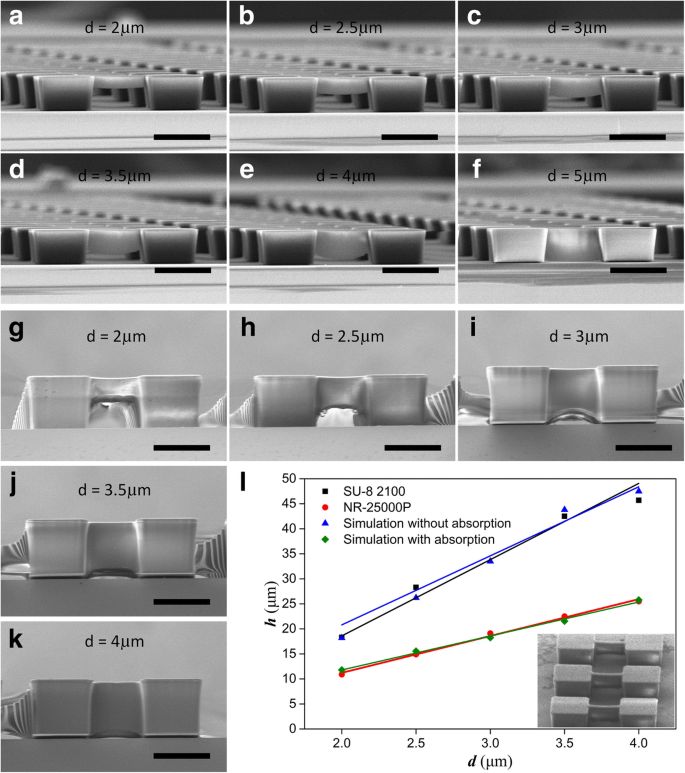

매달린 포토레지스트 빔은 서로 다른 선폭 d을 가진 1단계 회절 리소그래피로 생성됩니다. 그림 3b의 마스크 패턴을 사용합니다. a 아래의 NR26-25000P 포토레지스트 빔 d =2 μm, b 2.5 μm, c 3 μm, d 3.5 μm, e 4 μm 및 f 5 μm; g 아래의 SU-8 2100 포토레지스트 빔 d =2 μm, h 2.5 μm, i 3 μm, j 3.5 μm 및 k 4 μm; 나 흡수가 없는 시뮬레이션, NR26-25000P, SU-8 2100 및 흡수 계수 α가 있는 시뮬레이션에서 노출 두께 대 선폭의 함수 =0.0374 μm⁻¹ , 여기서 삽입은 SU-8 현수 빔의 기울어진 보기를 보여줍니다. 마스크 패턴의 선폭에 따라 빔의 두께가 증가한다. 눈금 막대는 50 μm

입니다.

그런 다음 흡수 계수 α를 소개합니다. 광학 모델에서 식 (8)로 계산을 수행합니다. α 아래의 결과 =0.0374 μm⁻¹ (UV-visible spectrophotometer, UV 2600, Shimadzu Co., Ltd.로 테스트한 365 nm에서 NR21-25000P의 흡수 계수)는 그림 4l에 나와 있으며, 여기서 R의 적합선 ² =0.986은 NR26-25000P의 실험결과와 잘 일치한다. 따라서 우리의 방법은 시뮬레이션을 통해 노출 깊이를 안내할 수 있는 1단계 노출로 매달린 구조를 제작하기 위해 거의 모든 종류의 두꺼운 네거티브 포토레지스트에 사용할 수 있습니다.

그림 5a–c는 z에서 다양한 교차 연결 패턴과 해당 시뮬레이션 결과를 표시합니다. =15 μm. 3개의 라인을 나란히 쌓아 넓은 현수 빔을 제작합니다. 여기서 라인 너비와 간격 너비는 모두 2 μm입니다. 20μm 원의 교차 연결 패턴은 매달린 빔을 지지하는 기둥을 제작하는 데 사용됩니다(그림 5a). 중공 교차 연결 패턴은 그림 5b, c에 표시된 것처럼 매달린 메쉬를 제작하도록 설계되었습니다. 얻어진 NR26-25000P 포토레지스트 연결은 그림 5d-f에 표시되어 있으며, 여기서 빔과 함께 교차 연결의 표면 텍스처가 시뮬레이션과 잘 일치하여 명확하게 관찰될 수 있습니다(그림 5a-c). 세 가지 유형의 교차 연결이 있는 매달린 메쉬가 그림 5g–i에 표시되고 지지 기둥도 예상대로 얻어집니다(그림 5g). 그림 5h는 높은 비율의 조밀한 패턴으로 인해 교차 연결 아래의 얇은 기둥을 보여줍니다. 그림 5c의 교차 연결 패턴은 듀티 비율이 낮고 빛의 세기가 약하여 완전히 매달린 메쉬가 생성됩니다(그림 5f). 따라서 교차 연결 패턴의 비율을 줄여서 완전히 매달린 구조를 제작할 수 있고 지지 기둥은 견고한 연결로 쉽게 형성할 수 있습니다. 한편, 적층된 라인 패턴의 수를 조정하여 빔의 너비도 제어할 수 있습니다.

<그림>

NR26-25000P와 다른 교차 연결 패턴. 아 –ㄷ 마스크의 세 가지 교차 연결 패턴과 z에서의 해당 시뮬레이션 결과 =15 μm, 여기서 선 너비는 2 μm이고 간격은 2 μm이고 z입니다. 단면 평면과 포토 마스크 사이의 거리입니다. d –f 스케일 바가 20 μm인 곳에서 얻은 포토레지스트 교차 연결 및 넓은 빔의 텍스처. 지 지지 기둥이 있는 매달린 메쉬. 아 얇은 지지 기둥이 있는 매달린 메쉬. 기둥은 높은 비율의 조밀한 교차 연결 패턴으로 인해 발생합니다. 나 완전히 매달린 메쉬 패턴. g의 눈금 막대 –나 100 μm

일부 복잡한 3D 미세 구조는 단일 노출(그림 6a–c, e, f) 또는 2단계 노출(그림 6d) 방법을 통해 제작되었습니다. 기울기 두께가 있는 매달린 빔이 그림 6a에 나와 있으며, 여기서 선 패턴의 너비는 두 영역에서 2~4 μm 및 4~6 μm입니다. 부유층의 두께는 그림 4에 표시된 결과와 같이 선폭이 증가함에 따라 증가합니다. 부유 동심원 및 부유 단어 패턴도 쉽게 준비할 수 있습니다(그림 6b, c). 두 개의 노출 프로세스를 결합하여 두 개의 매달린 레이어가 그림 6d와 같이 NR26-25000P와 통합되었습니다. 1차 노광이 완료된 후 2차 층이 제 1층에 스핀 코팅되어 노광된다. 적층된 메쉬는 두 번의 노출 프로세스와 현상 프로세스 후에 달성됩니다. 두 번째 노출은 첫 번째 레이어에 손상을 줄 수 있으므로 보다 우수한 다층 서스펜션 구조를 제작하려면 구조를 신중하게 최적화해야 합니다. 단어 패턴이 있는 SU-8 포토레지스트 매달린 메쉬도 성공적으로 달성되었지만(그림 6d–f), 높은 투명도로 인해 노출 매개변수를 제어하는 것이 NR26-25000P보다 더 어렵습니다.

<그림>

3D 매달린 포토레지스트 구조. 아 기울기 두께가 있는 매달린 빔, b 매달린 동심원, c 일시 중단된 단어 구조 및 d 포토레지스트가 NR26-25000P인 다층 부유 메쉬. 이 매달린 SU-8 메쉬. 에 매달린 SU-8은 단어 패턴과 맞물립니다. 눈금 막대는 100 μm입니다. d의 매달린 구조물 2단계 노출로 이루어지며 나머지는 1단계 노출로 제작됩니다.

이전 연구[2, 11, 22, 23]와 비교하여 우리는 작은 마스크 패턴의 회절을 이용하여 포토레지스트에 3D 광도 분포 모델을 형성합니다. 3D 매달린 구조는 시뮬레이션을 통해 잘 제어하고 예측할 수 있습니다. 포토레지스트의 흡수 계수도 여기에서 고려됩니다. Gradient Beam과 같은 다양한 두께의 현수구조물을 One-Step 노광으로 쉽게 형성할 수 있습니다. 또한 노광 공정은 일반적인 접촉 노광 방식에서 일반 마스크로 진행되며 특별한 마스크나 장비가 필요하지 않아 높은 제작 해상도와 호환성이 뛰어납니다.

열분해 탄소 구조

SU-8은 탄소 미세구조 제작을 위한 전형적인 전구체인 반면, NR26-25000P와 같은 다른 포토레지스트는 고온에서 구조를 유지할 수 없습니다. 그림 7a-c는 매달린 SU-8 구조를 보여주고 해당 열분해 탄소 구조는 그림 7d-f에 나와 있습니다. 열분해 과정에서 탈수소화, 고리화, 축합, 수소 이동 및 이성질화를 포함한 여러 동시 반응으로 인해 큰 수축이 발생합니다[8, 28]. 따라서 열분해 구조, 특히 비대칭 구조에 상당한 잔류 응력이 존재합니다. 열분해 탄소 빔은 수축되어 양쪽 끝의 기둥을 당겨 바닥에 균열을 일으킵니다(그림 7d). 대규모 메쉬의 경우 응력이 각 방향에서 상대적 균형을 유지하고 열분해 탄소 구조에서 명백한 균열이 발견되지 않습니다(그림 7e, f). 그림 7g–i와 같이 12 mm × 20 mm 크기의 독립형 탄소 메쉬가 달성됩니다. 탄소 메쉬의 면저항은 약 182 Ω/sq이고, 광선 투과율은 전체 파장에서 ~ 67%에 이릅니다. 준비된 우수한 전도성과 투명도를 가진 탄소 메쉬는 전극으로 페로브스카이트 태양 전지에 적용할 수 있으며[29,30,31], 반투명 태양 전지를 제조하는 데 사용할 수 있는 방법을 제공합니다. 또한, 준비된 탄소 메쉬는 유연성이 뛰어나 유연한 투명 전극의 응용 분야에서 큰 잠재력을 보여줍니다.

<그림>

매달린 SU-8 메쉬 및 열분해 탄소 메쉬. 아 매달린 SU-8 빔. ㄴ , ㄷ 지지 기둥이 있는 매달린 SU-8 메쉬. d 탄소 구조에 큰 변형이 남아 있고 기둥 바닥에 균열이 발생한 서스펜션 탄소 빔. 이 , f 매달린 탄소 메쉬. 지 열분해 후 독립형 탄소 메쉬. 아 독립형 탄소 메쉬의 확대. 나 유연성과 투명성이 우수한 12 mm × 20 mm 독립형 탄소 메쉬. 눈금 막대는 100 μm

입니다.

결론

요약하면, 우리는 새로운 1단계 마스크 기반 회절 리소그래피 방법을 통해 매달린 구조의 제조를 시연했습니다. 포토레지스트의 3D 광도 분포를 시뮬레이션하여 d 아래의 라인 패턴 너비가 증가함에 따라 노출 깊이가 증가함을 보여줍니다. <5 μm. 이 현상은 정의된 두께의 SU-8 포토레지스트를 가진 부유 구조를 제작하는 데 활용될 수 있으며, 이는 거의 투명하고 그레이스케일 리소그래피로 부유 구조를 형성하기 어려웠습니다. 여기에 해당하는 실험도 수행되었습니다. 매달린 SU-8 빔의 두께는 시뮬레이션 결과에 매우 가깝지만 NR26-25000P의 두께는 시뮬레이션의 노출 깊이보다 훨씬 얇다는 것을 발견했습니다. 이는 NR26-25000P의 높은 광흡수 특성 때문입니다. 그런 다음 포토레지스트의 흡수 계수를 광학 모델에 도입했으며 시뮬레이션 결과는 실험과 잘 일치했습니다. 지지 기둥이 있거나 없는 매달린 3D 메쉬를 제작하기 위해 세 가지 다른 교차 연결 패턴이 설계되었으며 표면 질감이 잘 복제되었습니다. 기둥이 있는 메쉬와 완전히 매달린 메쉬도 성공적으로 구현되었습니다. 기울기 두께의 현수 빔, 현수 동심원 링 및 현수 단어 구조를 포함한 다른 복잡한 3D 현수 포토레지스트 구조는 1단계 마스크 기반 회절 리소그래피를 통해 얻었습니다.

탄소 부유 구조와 독립형 탄소 메쉬는 전형적인 2단계 열분해 공정으로 추가로 제작되었습니다. 매달린 3D 탄소 구조는 표면적이 넓기 때문에 전기 화학 전극, 슈퍼 커패시터 및 센서에 적용될 수 있습니다. 독립형 메쉬는 우수한 전도성, 유연성 및 높은 투명도를 나타냅니다. 따라서 우리는 투명 전극, 반투명 태양 전지 및 에너지 저장 장치의 응용 분야에서 큰 잠재력을 보여준 3D 현수 구조 및 탄소 메쉬의 제조를 위한 간단하고 유망한 방법을 개발했습니다.

약어

3D:: 3차원
C-MEMS:: 탄소 미세 전자 기계 시스템

집중된 방위각으로 편광된 빔에 의해 조명된 실리콘 나노구의 자기 쌍극자 공명에서 금속 기판 유도 선폭 압축 계층적 물리적 상호작용을 통한 우수한 기계적 특성과 빠른 자가 치유력을 갖는 폴리(아크릴산)/질화붕소 복합 하이드로겔 제조

나노물질