단일 분자 자기 터널링 접합에서 제어 가능한 스핀 스위칭

초록

두 개의 일반 금속 전극에 결합된 단일 분자 자석(SMM)으로 구성된 새로운 유형의 스핀 전류 필터가 제안되었습니다. 이 터널링 접합은 SMM에 적용된 자기장 및 게이트 전압을 통해 스핀 분극이 전환될 수 있는 고도로 스핀 분극된 전류를 생성할 수 있음을 보여줍니다. SMM 터널 접합에서 이러한 스핀 스위칭은 SMM의 가장 낮은 비점유 분자 궤도를 통한 스핀 선택적 단일 전자 공명 터널링에서 발생합니다. 전자 전류 스펙트럼은 외부 자기장이 없는 상태에서도 여전히 스핀 분극화되어 있으며, 이는 분자의 스핀 상태가 기저 상태 이중선 $|\pm S\rangle$에 도달했는지 판단하는 데 도움이 될 수 있습니다. 이 장치는 현재 기술로 구현될 수 있으며 스핀트로닉스 및 양자 정보에 실용화될 수 있습니다.

소개

재료과학의 발달로 나노크기의 분자전자소자는 나노크기의 소자 및 스핀트로닉스에서의 잠재적인 응용과 관련하여 최근 몇 년 동안 광범위하게 연구되어 왔다[1,2,3]. 작은 크기와 낮은 전력 소비로 인해 음의 차동 저항이 있는 터널 접합[4], 정류기[5], 증폭기[6] 및 데이터 저장[7]을 포함하여 분자를 사용하는 많은 기본 장치가 입증되었습니다. 기존의 반도체 소자와 달리 단일 분자로 구성된 분자 소자는 제어 가능한 분자 스위치로 기능하기에 매우 적합한 것으로 보인다[8]. 분자 규모의 스위칭이 원자 양자점 접촉에서 보고되었지만[9,10,11], 단일 분자 접합은 분자 설계를 통해 on/off 전도 상태를 조정하는 능력의 추가적인 유연성을 제공합니다. 지난 수십 년 동안 개별 분자를 통과하는 전류 흐름의 성공적인 측정에 따라 광 제어 분자 스위치[12] 및 기계적으로 제어되는 단일 분자 스위치[13]와 같은 다양한 종류의 분자 스위치가 보고되었습니다. 높은 컨덕턴스와 낮은 컨덕턴스 상태 사이에서 장치를 전환합니다. 그러나 이러한 모든 스위칭 방식은 스핀 종속 전송 기능이 아닌 전하 전송 컨덕턴스의 조정만 가능하게 합니다.

최근 몇 년 동안 단일 분자 자석(SMM)으로 알려진 새로운 유형의 분자 물질이 분자 기반 스핀트로닉스 소자의 기본 구성 요소로 적절한 후보로 입증되었습니다[14]. 다른 분자와 달리 SMM은 상대적으로 순 스핀 모멘트가 큰 분자입니다(스핀 수 S ) 및 상당한 단축 자기 이방성 [15]. 저온에서 SMM은 두 개의 준안정 스핀 상태 $|\pm S\rangle$ [16] 중 하나에 갇힐 것입니다. 이러한 쌍성 때문에 SMM은 메모리 셀에 적합한 기반이 되었고[17, 18] SMM의 다른 물리적 특성을 조사하려는 많은 노력을 하게 되었습니다. 지금까지 SMM과 일반 금속[19,20,21] 또는 초전도체[22] 계면 사이의 전자 전이가 실험적으로 조사되었으며 자기장과 전기에 의해 SMM에 정보를 쓰고 읽는 기능이 있습니다. 편향은 $\hbox {TbPc}_{{2}}$ 분자에서도 입증되었습니다[23]. 이러한 연구에서 영감을 받아 SMM에서 터널링 전류의 스핀 분극화도 자기장과 게이트 전압에 의해 전환될 수 있을 것으로 예상됩니다. 그러나 이러한 SMM 터널링 접합을 기반으로 하는 제어 가능한 스위칭 방식은 아직 제안되지 않았습니다.

방법

이 편지에서 우리는 분자에 인가된 외부 자기장을 변경하여 순수한 스핀업 및 스핀다운 전자 전류 사이를 전환하는 데 사용할 수 있는 SMM 터널 접합에서 새로운 유형의 스핀 전환 효과를 제시합니다. 그림 1a와 같이 이 나노구조는 두 개의 일반 금속 전극에 연결된 SMM으로 구성됩니다. SMM의 에너지 레벨은 게이트 전압에 의해 조정되고 SMM의 스핀 자화는 외부 자기장에 의해 전환될 수 있습니다. 그림 1b에서 이 장치의 자기장 제어 스핀 주입에는 2단계 방식이 필요하다는 것을 알 수 있습니다. 첫째, SMM의 스핀 방향을 "기록"하기 위해 상대적으로 더 큰 외부 자기장을 적용합니다. SMM의 코어 스핀은 자기장의 방향에 따라 두 개의 준안정 스핀 상태(\pm \,S\) 중 하나로 전환됩니다. 그리고 스핀 주입 프로세스는 자기장이 없는 상태에서 두 리드에 가해지는 전기 바이어스를 사용하는 것으로 구성됩니다. 두 리드의 다른 화학적 전위와 SMM의 자기 이방성으로 인해 SMM의 자화와 평행한 스핀을 가진 전자만 접합부를 통해 흐를 수 있어[14], 전류가 극성을 띄게 됩니다. 시스템의 전체 Hamiltonian은 [24, 25]

로 작성됩니다. $$\begin{정렬} H&=\varepsilon _{0}\sum _{\sigma }c_{\sigma }^{\dag }c_{\sigma }+Uc_{\uparrow }^{\dag }c_{ \uparrow }c_{\downarrow }^{\dag }c_{\downarrow } -{\mathcal {D}}(S^{z})^{2}-J {\mathbf {s}}\cdot {\ mathbf {S}} \nonumber \\&\quad -\Delta B(s^{z}+S^{z})+\sum _{k,\sigma ,\alpha }(t_{\alpha }a_{ \alpha k\sigma }^{\dag }c_{\sigma }+t^{*}_{\alpha }c^{\dag }_{\sigma }a_{\alpha k\sigma }) \nonumber \ \&\quad +\sum _{k,\sigma ,\alpha }\varepsilon _{k\sigma }a_{\alpha k\sigma }^{\dag }a_{\alpha k\sigma }. \end{정렬}$$ (1)

여기서 $\varepsilon _{0}$ 은 SMM에 인가되는 게이트 전압에 의해 이동될 수 있는 SMM의 최저 비점유 분자 궤도(LUMO)의 현장 에너지입니다. $c_{\sigma }^{\dag }$ ($c_{\sigma }$)는 전자 생성(소멸) 연산자이며 $\sigma$를 Pauli 스핀 지수로 사용합니다. 유 쿨롱 반발 에너지를 나타냅니다. ${\mathcal {D}}$는 자기 단축 이방성 매개변수입니다. 제 는 전도 전자의 스핀 사이의 교환 상호작용입니다. ${\mathbf {s}} =\sum \nolimits _{\sigma \sigma ^{\prime }}c_{\sigma }^{\dag }\sigma _{\sigma \sigma ^{\prime }}c_{\sigma ^{\prime }}/2$, LUMO 수준 및 로컬 스핀 ${\mathbf {S}}$. 분자의 쉬운 축이 스핀 공간의 z축이라고 가정하기 때문에 $\Delta B(s^{z}+S^{z})$ 적용된 자기장과 관련된 Zeeman 분할을 설명합니다. 이 쉬운 축을 따라, 여기서 g 계수와 보어 마그네톤 $\mu _{B}$은 $\Delta B$에 흡수됩니다. $a_{\alpha k\sigma }^{\dag }$ ($a_{\alpha k\sigma }$) 는 운동량이 k인 전자에 대한 생성(소멸) 연산자입니다. , 스핀 $\sigma$ 및 에너지 $\varepsilon _{k\sigma }$ 에서 리드 $\alpha$. $t_{\alpha }$로 표시되는 SMM과 일반 금속 리드 사이의 터널 결합 강도는 운동량 k와 무관합니다. 및 스핀 $\sigma$.

격리된 SMM의 Hamiltonian $H_{{\mathrm{mol}}}$, 즉 Eq.의 처음 5개 항을 대각화하기 쉽습니다. (1). ${\mathbf {S}}_{T}={\mathbf {s}}+{\mathbf {S}}$를 정의하면 고유값 m $S_{T}^{z}$의 $S_{T}^{z}$는 교환 관계로 인한 좋은 양자수 $[S_{T}^{z},H_{{\mathrm{mol}}}]=0$ . 다음 식에서 $|\bullet \rangle _{L({\mathrm{mol}})}$는 LUMO(SMM)의 스핀 상태를 나타냅니다. $n=0,1,2$가 LUMO의 전자 수로 정의되면 고유 에너지는 다음과 같이 얻을 수 있습니다[26]. $\varepsilon _{|0,m\rangle }=-{\ 고유 상태에 대한 수학 {D}}m^{2}-\Delta Bm$ $|0,m\rangle =|0\rangle _{L}\otimes |m\rangle _{{\mathrm{mol} }}$, $\varepsilon _{|1,m\rangle ^{\pm }}=\varepsilon _0 -\Delta B m+J/4-{\mathcal {D}}(m^{2} +1/4)\pm \Delta \varepsilon (m)$ 고유 상태 $|1,m\rangle ^{\pm }=C_{1}^{\pm }|\downarrow \rangle _{L }\otimes |m+1/2\rangle _{{\mathrm{mol}}}+C_{2}^{\pm }|\위쪽 화살표 \rangle _{L}\otimes |m-1/2\rangle _{{\mathrm{mol}}}$ 및 $\varepsilon _{|2,m\rangle }=2\varepsilon _0 +U-{\mathcal {D}}m^{2}-\Delta B m$ 고유 상태 $|2,m\rangle =|\uparrow \downarrow \rangle _{L}\otimes |m\rangle _{{\mathrm{mol}}}$. 여기서 $\Delta \varepsilon (m)=\sqrt{{\mathcal {D}}({\mathcal {D}}-J)m^{2}+(J/4)^{2}(2S +1)^{2}}$ 및 $C_{1}^{\pm }$ 및 $C_{2}^{\pm }$, Ref. [24], 효과적인 Clebsch-Gordan 계수로 작용합니다.

전송 프로세스는 SMM 수준을 통한 순차적 터널링에 의해 지배되는 반면 약한 cotunneling 및 직접 터널링은 안전하게 무시할 수 있습니다. SMM과 리드 간의 약한 결합의 경우 마스터 방정식 접근 방식이 적용됩니다. SMM을 통해 흐르는 총 스핀-$\sigma$ 전류는 $I_{\sigma }=(I_{L\sigma }-I_{R\sigma })/2$로 쓸 수 있습니다. 여기서 $ I_{L\sigma }$ ($I_{R\sigma }$)는 스핀-$\sigma$ 전류가 왼쪽(오른쪽) 리드에서 SMM으로 흘러들어옴을 나타내며,

$$\begin{정렬} I_{\alpha \sigma }=-(e/h)\sum _{i,f}(n_{i}-n_{f})R_{\alpha \sigma }^{f \rightarrow i}P_{f}, \end{정렬}$$ (2)

총 전류가 $I=\sum _{\sigma }(I_{L\sigma }-I_{R\sigma })/2$이고 전류의 스핀 분극 계수가 $\ eta =\frac{ I_{\alpha \uparrow } - I_{\alpha \downarrow }}{ I_{\alpha }} \times 100\%$. 식에서 (2), $R_{\alpha \sigma }^{f\rightarrow i}$는 $|i\rangle$과 $|f\rangle$ 상태 사이의 전이율을 나타내며, $ R_{\alpha \sigma }^{f\rightarrow i}=\Gamma _{\alpha \sigma }[f(\varepsilon _{i}-\varepsilon _{f}-\mu _{\alpha })\ langle i|c_{\sigma }^{\dag }|f\rangle ^{2}+f(\varepsilon _{i}-\varepsilon _{f}+\mu _{\alpha })\langle f| c_{\sigma }^{\dag }|i\rangle ^{2}]$, 여기서 $\Gamma _{\alpha \sigma }=2\pi D_{\alpha \sigma }|t_{\alpha }|^{2}$는 리드 $\alpha$에 대한 선폭 함수이며 $D_{\alpha \sigma }$는 $E_{F}$에서의 상태 밀도입니다. 그리고 $f_{\alpha }$는 온도 $T_{\alpha }$ 및 화학 포텐셜 $\mu _{\alpha }$에서 납 $\alpha$의 페르미 함수입니다. $P_{i}$는 상태 $|i\rangle$에서 SMM을 찾을 확률을 나타냅니다. Timm[26]과 Shen[27]이 제안한 수치적 방법에 따라 확률 $P_{i(t)}$과 정상 상태 확률 $P_{i(t\rightarrow \infty)의 시간 의존성 )}$는 일련의 속도 방정식 ${\mathrm{d}}P_{i}/{\mathrm{d}}t=\sum _{f}R_{i,f}P_ {i}$.

여기에서 스핀 수 $S=10$, ${\mathcal { D}}=0.06$ meV, $J=0.1$ meV 및 $U=25$ meV. 고려 중인 전극은 일반 금속으로 만들어지므로 선폭 함수는 스핀과 무관합니다. 즉, 단순성을 위해 $\Gamma _{\alpha \sigma }=\Gamma _{0}$입니다.

<그림>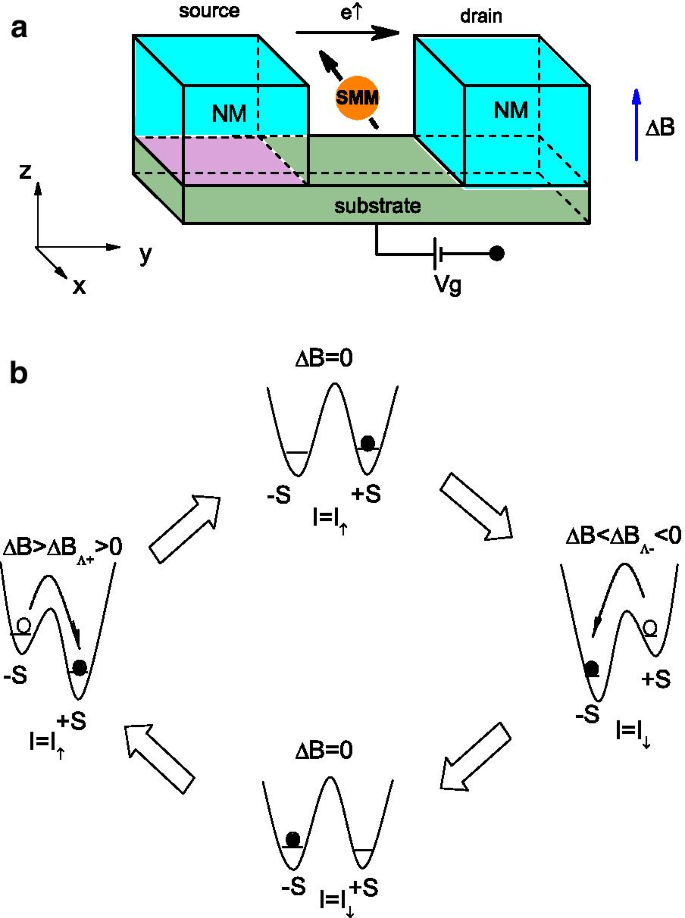

아 한 쌍의 비자성 전극에 결합된 SMM으로 구성된 스핀 필터 또는 스핀 메모리의 개략도. ㄴ SMM의 자화 스위칭 및 외부 자기장에 의한 터널링 전류의 스핀 분극화에 대한 개략도

<그림>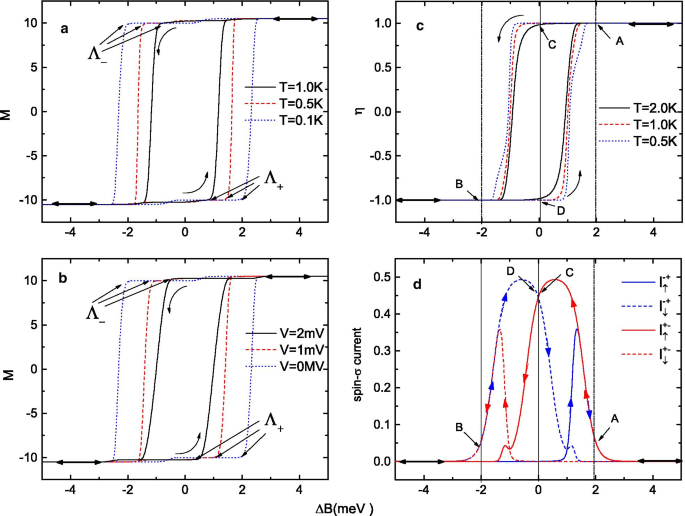

아 , b a에 대한 SMM의 자기 히스테리시스 루프 다른 평형 온도 및 b 외부 자기장 $\Delta B$이 앞뒤로 스캔될 때 다른 바이어스 전압. ㄷ 다양한 평형 온도 및 d에 대한 터널링 전류의 스핀 분극 스핀-$\sigma$ 전류($e\Gamma_{0} /\hbar$로 조정됨) at $T=0.5$ K, 외부 자기장 $\Delta B$이 다시 스캔될 때 $V=1$ mV

의 고정 바이어스에서 앞뒤로 <그림>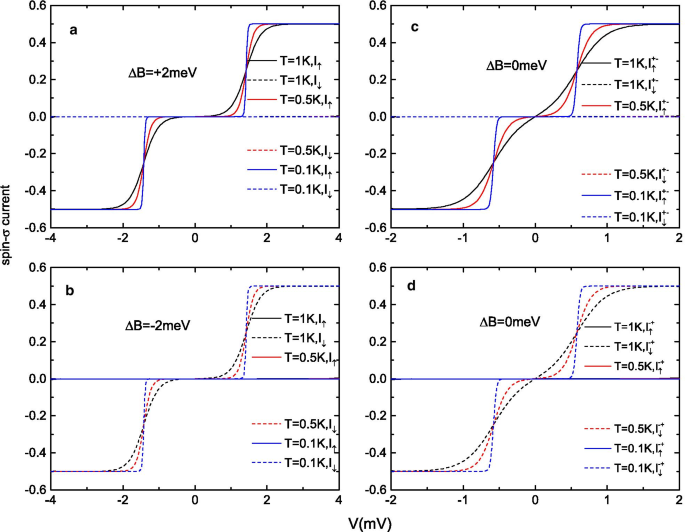

Spin-$\sigma$ 전류 $I_{\uparrow (\downarrow )}$ ($e\Gamma_{0} /\hbar$로 축척) (a , b ) a의 외부 자기장이 있는 경우 $\델타 B=+2$ meV, b $\Delta B=-\,2$ meV, c , d 바이어스 전압의 함수로 자기장이 없는 경우

<그림>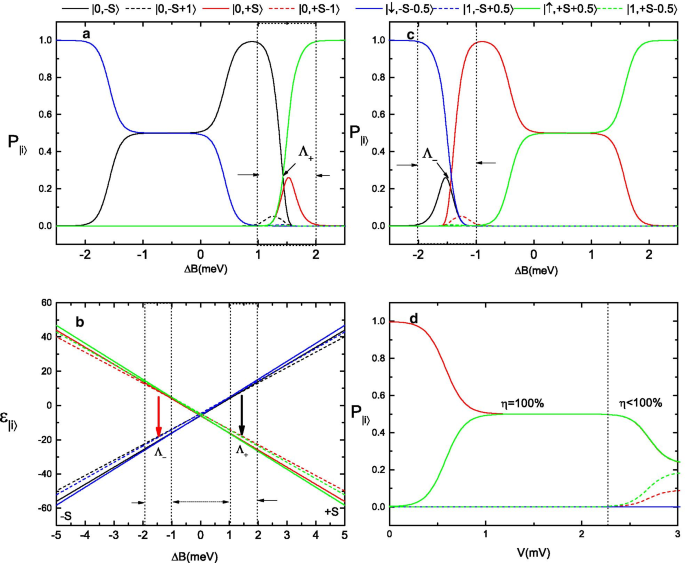

아 , ㄷ 분자 상태 확률의 변화 a $\Delta B$가 ${-}\,5$ meV에서 ${+}\,5$ meV 및 c로 스캔되기 때문에 $\Delta B$가 $+\,5$ meV에서 ${-}\,5$ meV로 스캔되기 때문입니다. ㄴ $\Delta B$로 이러한 스핀 상태에 대한 Zeeman 다이어그램은 ${-}$ 5 meV에서 ${+}$ 5 meV로 변경됩니다. d 분자의 스핀 상태가 $P_{|0,+S\rangle }=1$ 및 $P_{i}=0$<과 같이 초기에 준비될 때 바이어스 전압의 함수로서의 분자 상태 확률의 변화

<그림>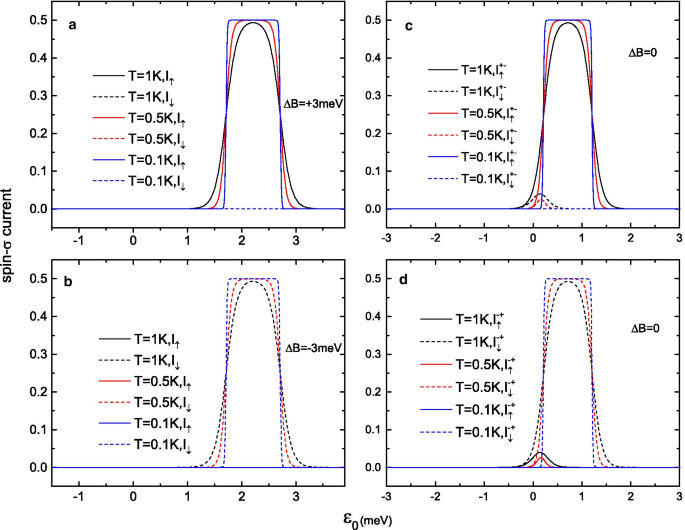

회전$\sigma$ 전류 $I_{\uparrow (\downarrow )}$ a , b a의 외부 자기장이 있는 경우 $B=+2$ meV 또는 b $B=-\,2$ meV 및 c , d 분자 수준 $\varepsilon _{0}$

의 함수로 자기장이 없을 때

결과 및 토론

먼저 자기장 $\Delta B$를 사용하여 SMM의 스핀 상태를 "기록"하는 방법을 보여줍니다. 그림 2에서 SMM의 자화, 전류의 스핀 분극화 $\eta$ 및 스핀-$\sigma$ 전류를 바이어스가 있는 $\Delta B$의 함수로 플로팅합니다. 접합부에 가해지는 전압. 화살표는 자기장의 스캐닝 방향을 나타내며 스캐닝 프로세스는 시스템이 정상 상태로 이완될 수 있을 만큼 충분히 느린 것으로 가정됩니다. 그림 2a–c에서 자기장 $\Delta B$이 앞뒤로 스캔될 때 분자의 자화와 전류의 스핀 분극이 모두 루프 구조를 나타내는 것으로 나타났습니다. 설명의 편의를 위해 SMM의 자화가 $+S\rightarrow -S$ 및 $\Lambda _{+}\에서 전환될 때 반전 지점을 표시하기 위해 \(\Lambda _{-}$를 사용합니다. ) $-S\rightarrow +S$의 반전 지점을 나타냅니다. SMM의 자화는 그림 2a, b에서 다양한 평형 온도와 바이어스 전압에 대한 $\Delta B$의 함수로 표시됩니다. 열 변동과 전기 바이어스는 모두 자기 반전을 활성화할 수 있음이 분명합니다. 델타 B)가 활성화 에너지에 정확히 도달하기 전에. 결과적으로, 자기 히스테리시스 루프는 평형 온도 또는 바이어스 전압이 증가함에 따라 수축하고 $\Lambda _{+}$와 $\Lambda _{-}$ 사이의 거리가 감소합니다. 그러나 자기 히스테리시스 루프가 얼마나 축소되더라도 터널링 전류의 스핀 분극 계수는 $\Delta B$가 가까울 때를 제외하고 항상 $\eta =\pm 100\%$의 매우 높은 값에 도달할 수 있습니다. 두 개의 반전 지점 $\Lambda _{+}$ 및 $\Lambda _{-}$. 또한, 작은 자기장 영역에서 전류의 스핀 분극은 $\Delta B_{\Lambda _{-}}<\Delta B<\Delta B_{\Lambda _{+}}\ )는 큰 자기장 영역 \(\Delta B<<\Delta B_{\Lambda _{-}}$ 또는 $\Delta B>>\Delta B_{\Lambda _{ +}}$. 그림 2c와 같이 대 자기장 영역에서 터널링 전류의 스핀 분극 계수 는 다음과 같이 요약할 수 있습니다.

<그림>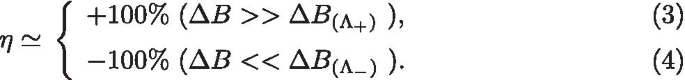

예를 들어 이 영역에서 그림 2c, d의 지점 A(지점 B)에서 주어진 외부 자기장 $\Delta B$은 분자의 단일 결정적 자화에 해당하며 $100 \%$ 스핀업(스핀다운) 전자 전류는 접합부를 통해 흐를 수 있습니다. 그러나 낮은 자기장 영역 $\Delta B_{\Lambda _{-}}<\Delta B<\Delta B_{\Lambda _{+}}$에서 SMM의 원래 자화는 유지될 수 있습니다. 변경되지 않고 $+S$ 및 $-S$ 스핀 방향이 모두 유지될 수 있습니다. 그림 2d에서 고정 평형 온도 $T=1$ K 및 전압 $ V=1$ mV. 주어진 단일 $\Delta B$가 분자의 두 가지 가능한 자화에 해당한다는 것이 명확하게 표시됩니다. $\Delta B$가 $+5$ meV에서 $ -5$ meV 및 $I_{\sigma }^{-+}$ 자기장이 반대 방향으로 스캔될 때 전류를 나타냅니다($\Delta B$가 -5 meV에서 +5로 변경됨 meV), 그러면 $+S$ 또는 $-S$에서 SMM의 두 스핀 방향 모두 낮은$\Delta B$ 영역(예:점에서 그림 2c, d)의 C와 D. 그림 2c에서, 작은 자기장 영역에서 터널링 전류의 스핀 분극 계수 $\eta$ $\Delta B_{\Lambda _{-}}<\Delta B<\Delta B_{\ Lambda _{+}}$는 다음과 같이 요약될 수 있습니다.

<그림>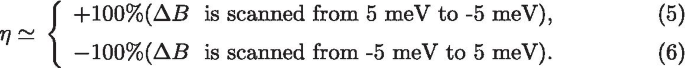

더 중요한 것은 그림 2d에서 볼 수 있듯이 C 또는 D 지점인 $\Delta B=0$에서의 터널링 전류 강도가 $V=1$ mV의 동일한 바이어스 전압. 이것은 이 소자가 외부 자기장이 없을 때 보다 쉽게 스핀 분극 전자 전류를 생성할 수 있음을 의미하므로 스핀 필터 또는 스핀 메모리 소자로 적합합니다.

이 분자 접합의 스핀 주입 기능을 논의하기 위해 일정한 게이트 전압과 더 낮은 온도에서 바이어스 전압의 함수로 스핀-$\sigma$ 전류를 표시합니다. 그림 3a, b는 $I_{\uparrow (\downarrow )}$-V 큰 자기장 값 $\Delta B=\pm 2$ meV에서의 곡선(그림 2의 점 A 및 B에서의 자기장에 해당)인 반면, 그림 3c, d는 \가 없을 때의 곡선을 보여줍니다. (\Delta B\) (그림 2의 C 및 D 지점에 해당). 어떤 자기장 체제를 선택하든 스핀 필터링 기능은 분명합니다. 그림 3a(그림 3b)에서 볼 수 있듯이 스핀업(스핀다운) 전자만 접합부를 통해 흐를 수 있는 반면 다른 스핀 방향의 전자 전류는 SMM의 스핀 선택도에 의해 완전히 0으로 억제됩니다. $+S$ ($-S$) 방향. 자기장 $\Delta B$가 $+S$ 및 $-S$ 방향에서 0으로 감소될 때 유사한 결과가 그림 3c, d에서 얻어집니다. $\Delta B$가 없으면 SMM은 두 쌍안정 접지 상태 $M=\pm S$ 중 하나에 갇혀 있어야 합니다. 이러한 이유로 SMM의 $+S$ 및 $-S$ 스핀 방향은 $\Delta B=0$ 영역에서 잘 보존될 수 있습니다. 예를 들어 $+5$ meV에서 0으로 $\Delta B$를 스캔하면 $M=+S$가 저장되고 완전히 극성화된 스핀업 전류가 얻어집니다(그림 3c 참조). ). 또한, 바이어스 전압이 증가하면 외부 자기장이 없는 상태에서 전자 전류는 큰 자기장의 경우보다 더 빨리 상대적으로 높은 전류 안정기에 도달한다. 그림 3b, d에서 볼 수 있듯이 $\Delta B=0$ meV 및 $\Delta B=-\,2$ meV 영역 모두에서 스핀업 전류가 없지만 $I_ {\downarrow }$ 그림 3d의 전류는 $V\약 0.7$ mV에서 최대 $0.5e \Gamma _{0}/\hbar$에 도달할 수 있지만 그림 3c에서 최소 $V>1.5$mV의 더 큰 바이어스 전압이 필요합니다.

그림의 기본 물리학을 명확히 하기 위해. 2와 3에서 분자 상태 확률 $P_{|0,\pm S\rangle }$, $P_{|0, S-1\rangle }$, $P_{|0, - S+1\rangle }$, $P_{|\uparrow , S+1/2\rangle }$, $P_{|\downarrow , -S-1/2\rangle }$, $ P_{|1, S-1/2\rangle }$ 및 $P_{|1, -S+1/2\rangle }$는 자기장이 스캔될 때 $\Delta B$의 함수입니다. 고정 평형 온도 $T=0.5$ K 및 바이어스 전압 $V=1$ mV에서 앞뒤로. 그림 4a에서 $\Delta B$는 시스템이 정상 상태로 이완될 수 있도록 충분히 천천히 $-5$ meV에서 $+5$ meV로 스캔됩니다. 큰 자기장 영역 $\Delta B<-2$ meV에서 모든 상태의 확률은 $P_{|\downarrow , -S-1/2\rangle }=1을 제외하고는 0과 같습니다. $, 이는 SMM의 스핀 상태가 $-S$ 방향으로 고정되고 스핀다운 전자 하나가 외부 자기장에 의해 분자의 LUMO 준위에 갇히는 것을 의미합니다. 쿨롱 반발 에너지($U=25$ meV)의 상대적으로 큰 값과 LUMO 준위에 갇힌 스핀-다운 전자의 경우 SMM 수준에서는 스핀-업 전자가 존재할 수 없고 전자 전류가 차단됨 . $\Delta B$가 $-2$ meV에서 1meV로 증가하면 0이 아닌 분자 상태 확률 $P_{|0,-S\rangle }$이 나타나고 전자 전류는 $\varepsilon _{|0,-S\rangle }\leftrightarrow \varepsilon _{|\downarrow , -S-1/2\rangle }$ 전환. 이 $\Delta B$ 창에서 SMM의 스핀 상태는 여전히 $-S$ 방향으로 저장될 수 있지만 스핀다운 전자는 SMM을 통해 터널링되어 순수한 스핀다운 극성 전자 전류를 생성할 수 있습니다. . 그러나 $\Delta B$가 $[1\,{\text {meV}}, 2\,{\text {meV}}]$ 범위로 더 증가하면 비탄성 터널링 프로세스는 분자 스핀의 자기 전환이 발생합니다. 이 체제에서 SMM의 거의 모든 스핀 상태는 점유될 가능성이 있으며 두 개의 특수 상태인 $P_{|0,-S\rangle }$ 및 $P_{|\uparrow , +S+1/2\rangle }$, 다른 상태보다 훨씬 큽니다. 더 흥미롭게도 $P_{|0,-S\rangle }=P_{|\uparrow , +S+1/2\rangle }$ 이 지점 $\Lambda _{+}\ ) 그림 2a에서 분자의 자화가 \(-S$에서 $+S$로 역전되기 시작함을 나타냅니다. $\Delta B$가 2meV 이상으로 계속 증가함에 따라 $P_{|\uparrow , S+1/2\rangle }\rightarrow 1$을 제외한 모든 상태의 확률은 0으로 감소합니다. 스핀 상태는 $+S$ 방향으로 고정되고 터널링 전류는 분자의 LUMO 레벨을 차단하는 스핀업 전자 하나에 의해 "꺼짐"으로 전환됩니다. 반면 자기장이 $+5$ meV에서 $-5$ meV로 스캔되면(그림 4c 참조) 비슷한 과정이 다시 발생하고 반전 지점 $\Lambda _ {-}$는 $P_{|0,+S\rangle }=P_{|\downarrow , -S-1/2\rangle }$인 지점에 해당합니다. 그림 4b에는 이러한 스핀 상태에 대한 Zeeman 다이어그램이 나와 있습니다. SMM의 큰 자기 이방성으로 인해 양자수 $M =\pm S$ ($S=10$ for $\hbox {Mn}_{{12}}\ )-Ac)는 \(DS^{2}_{z}\approx 60$ K의 에너지 장벽에 의해 여기 상태에서 잘 분리됩니다. 또한 자기 스위칭 포인트 $\Lambda _{(+)- }$는 그림 4에서 대략 1.3meV이며, 이는 단일 자기 원자의 역전점 $2S|{\mathcal {D}}|$에 가깝습니다. 그림 4d에서 분자 상태 확률은 고정 온도 $T=0.5$ K와 자기장 $\Delta B=0$에 대한 바이어스 전압의 함수로 표시됩니다. SMM이 $+S$ 스핀 방향에 갇혀 있다고 가정하면 그림 4d의 전자 터널링 프로세스는 두 부분으로 나눌 수 있습니다. (i) 작은 바이어스 영역에서 $V<2.5\ ) mV, 전자 전류는 \(\varepsilon _{|0,+S\rangle }\leftrightarrow \varepsilon _{|\uparrow , S+1/2\rangle }$ 천이와 스핀- 위쪽 전자는 접합을 통해 터널링할 수 있습니다. (ii) 바이어스 전압이 큰 바이어스 영역 $V>2.5$ mV로 증가할 때 바이어스가 스핀 방향 $+S$과 $-S) 사이의 에너지 장벽을 극복할 만큼 크지는 않지만 $, $\varepsilon _{|0,+S-1\rangle }$ 및 $\varepsilon _{|1,+S와 같이 \(+S$ 방향으로 더 높은 에너지를 갖는 스핀 상태 -1/2\rangle }\)를 점유할 수 있으며, 이는 SMM을 통한 스핀다운 전자 터널링을 위한 추가 추가 채널을 도입할 것입니다. 결과적으로 바이어스 전압이 계속 증가함에 따라 터널링 전류는 계속 증가하지만 스핀 분극 계수 $\eta$는 감소합니다.

마지막으로, 게이트 전압(LUMO 레벨의 현장 에너지 \varepsilon _{0}\))는 외부 자기장이 있거나 없는 상태에서 계산됩니다(그림 5 참조). 저온에서 100$\%$ 스핀 극성 전자 전류는 다른 게이트 전압 창을 통해 "켜기/끄기"로 전환할 수 있습니다. $\Delta B=\pm 2$ meV가 적용되면 순수한 스핀$\sigma$ 전류가 $0.8\,{\text {meV}}<\varepsilon _ {0} <2.8\,{\text {meV}}$, 반면 $I_{\uparrow } =I_{\downarrow } =0$ 이 영역 밖에 있습니다. 평형 온도로 T 증가할수록 $I_{\sigma }$의 피크는 낮아지고 넓어지지만, 낮은 온도에서 볼 수 있는 높은 스핀 분극 전류는 여전히 유지됩니다(그림 5a, b 참조). 큰 자기장 영역과 달리 스핀-$\sigma$ 전류는 $-0.8\,{\text {meV}}<의 게이트 전압 창에서 외부 자기장 없이 "켜짐"됩니다. \varepsilon _{0} <1.8\,{\text {meV}}$이고 스핀 분극은 두 가지 다른 결과를 나타냅니다(그림 5c, d 참조). 게이트 전압 창에서 $0.8\,{\text {meV}}<\varepsilon _{0} <1.8\,{\text {meV}}$, $\pm \,100\%$ 스핀 분극 전자 전류는 그림 2c의 점 C와 D에 해당하는 V$=1$ mV의 작은 바이어스에서 생성될 수 있습니다. 그러나 $-0.8\,{\text {meV}}<\varepsilon _{0} <0.8\,{\text {meV}}$ 게이트 전압 창에서 상태 사이의 에너지 갭 $ |0,\pm S \rangle$ 및 $|1,\pm S\mp 0.5 \rangle$은 매우 작아지고 $+S$(또는 $- S$) 스핀 방향은 바이어스 전압을 통해 도달할 수 있습니다. 따라서 스핀업 전자와 스핀다운 전자 모두 SMM을 통해 터널링할 수 있습니다. 결과적으로, 전류의 총 스핀 분극 $\eta$은 이 게이트 전압 영역에서 감소합니다.

결론

요약하면, 우리는 스핀업 및 스핀다운 전류 스위칭에 대한 두 가지 "온" 상태와 전류 "오프" 상태를 갖는 3상 스위칭 효과를 제안했습니다. 이러한 스핀 분극 전류 스위칭은 SMM(예:$\hbox {Mn}_{{12}}$-Ac) 터널 접합에서 실현될 수 있으며 LUMO를 통한 스핀 선택적 단일 전자 공진 터널링에서 발생합니다. 에스엠엠. 이 3상 스위칭 동작은 스핀-궤도 상호 작용이나 자기 리드 없이 자기장과 게이트 전압을 통해 제어할 수 있으며, 미래의 스핀트로닉 회로에서 스핀 필터나 스핀 메모리와 같은 스핀트로닉 장치의 좋은 후보입니다.

데이터 및 자료의 가용성

현재 연구에서 사용된 데이터 세트는 이 기사의 교신 저자로부터 제공됩니다.

약어

SMM:: 단분자 자석
LUMO:: 가장 낮은 비어 있는 분자 궤도
Mn₁₂ -Ac:: [Mn₁₂ O₁₂ (CH₃ CO₂ )₁₅ (H₂ 오)₄ ]
TbPc₂ :: [(C₃₂ H₁₆ N₈ )₂ Tb^III ] 복합

ZnO 나노로드의 Mg 도핑은 분자 도킹 분석을 통해 개선된 광촉매 분해 및 항균 가능성을 입증했습니다. 물 분해를 위한 향상된 패턴 조촉매 TiO2/Fe2O3 광양극

나노물질