벤 다이어그램의 부울 관계

네 번째 예에는 A가 있습니다. 부분적으로 겹치는 B . 하지만 먼저 아래의 모든 해치 영역 전체를 살펴본 다음 나중에 겹치는 영역만 살펴보겠습니다. 아래와 같이 일부 부울 표현식을 위의 영역에 할당해 보겠습니다.

왼쪽 아래에는 A에 대한 빨간색 수평 해치 영역이 있습니다. . B에 대한 파란색 수직 해치 영역이 있습니다. .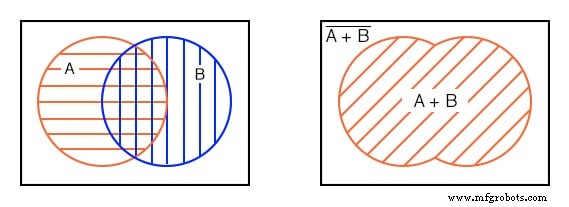

양쪽의 전체 영역을 보면 해치 스타일, 모든 해치 영역의 합계에 관계없이 포괄적인 OR에 해당하는 오른쪽 위의 그림을 얻습니다. A, B의 함수입니다. 부울 표현식은 A+B입니다. .

이것은 45 ^o 로 표시됩니다. 해치 영역. 빗금친 영역 외부의 모든 항목은 (A+B)-not에 해당합니다. 위에 표시된 대로. 네 번째 예시의 다음 부분으로 넘어가겠습니다.

겹치는 원이 있는 벤 다이어그램을 보는 다른 방법은 A 및 B , 왼쪽 아래 이중 해치 영역. AND에 해당하는 이 공통 영역에 대한 부울 표현식 함수는 AB입니다. 오른쪽 아래 그림과 같이. 이중 해치 AB 이외의 모든 항목 AB 아님 .

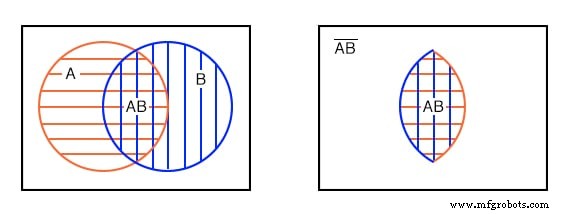
A의 일부 구성원은 , 위는 (AB)'의 구성원입니다. . B의 일부 구성원 (AB)'의 구성원입니다. . 그러나 (AB)'의 구성원 중 누구도 이중 해치 영역 AB 내에 있음 .

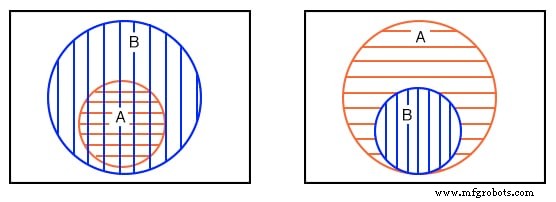
왼쪽 위의 두 번째 예를 반복했습니다. 이전에 스케치한 다섯 번째 예는 비교를 위해 오른쪽 위에 제공됩니다. 나중에 Karnaugh 지도의 다른 그룹에 완전히 포함된 비정기적 요소 또는 요소 그룹을 찾을 수 있습니다.

다음으로, 보완 변수를 포함하는 부울 표현식의 전개를 아래에서 보여줍니다.

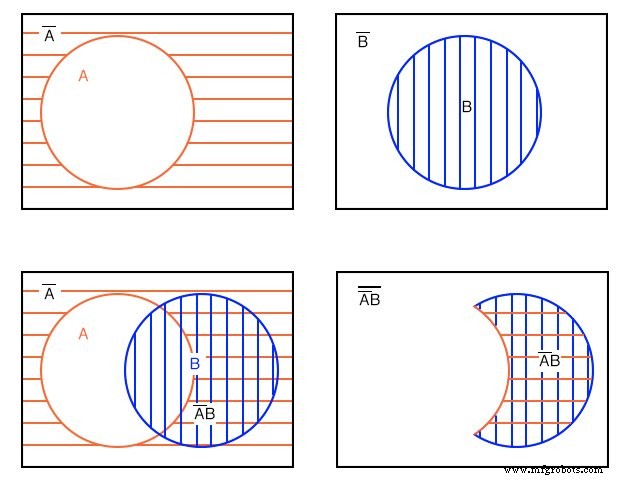
예: (위)

A'B에 대한 벤 다이어그램 표시 (A-not AND B).

해결책: 왼쪽 상단부터 시작하여 빨간색 수평 음영 A'가 있습니다. (A-not), 오른쪽 상단, B . 다음으로 왼쪽 하단에서 AND 함수 A'B를 형성합니다. 이전 두 영역을 겹쳐서 대부분의 사람들은 이것을 제시된 예에 대한 답으로 사용할 것입니다.

그러나 이중 해치 A'B만 명확성을 위해 맨 오른쪽에 표시됩니다. A'B 표현 A'가 있는 지역입니다. 및 B 겹친다. A'B 외부의 명확한 영역 (A'B)'입니다. , 이는 제시된 예의 일부가 아닙니다.

부울 OR과 유사한 것을 시도해 보겠습니다. 기능.

예: B'+A 찾기

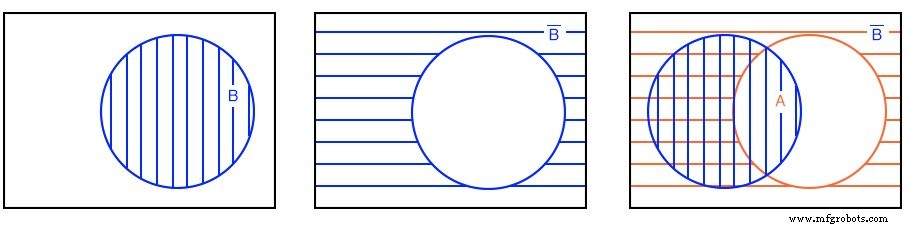
해결책: 오른쪽 위에서 B로 시작합니다. B'에 보완됨 . 마지막으로 A를 오버레이합니다. B' 위에 . OR을 형성하는 데 관심이 있기 때문에 기능을 사용하면 해치 스타일에 관계없이 모든 해치 영역을 찾습니다. 따라서 A+B' 오른쪽 위의 모든 해치 영역입니다. 명확성을 위해 왼쪽 아래에 단일 해치 영역으로 표시됩니다.

예: (A+B')' 찾기

해결책:

녹색 45 ^o A+B' 빗금친 영역은 이전 예의 결과입니다. to로 이동,(A+B')' ,왼쪽 위의 현재 예에서 A+B'의 보수를 찾아보겠습니다. , 이는 (A+B')'에 해당하는 왼쪽 위의 흰색 투명 영역입니다. .

오른쪽에서 AB'를 반복했습니다. 결과와 비교하기 위해 이전 예의 이중 해치 결과입니다. (A+B')'에 해당하는 지역 및 AB' 위의 왼쪽과 오른쪽은 각각 동일합니다. 이것은 DeMorgan의 정리와 이중 부정으로 증명할 수 있습니다.

이것은 요점을 제시합니다. 벤다이어그램은 실제로 아무 것도 증명하지 않습니다. 형식 증명에는 부울 대수가 필요합니다. 그러나 벤 다이어그램은 검증 및 시각화에 사용할 수 있습니다. 벤다이어그램으로 DeMorgan의 정리를 확인하고 시각화했습니다.

예:

부울 표현식 A'+B'는 무엇을 의미합니까? 벤다이어그램처럼 보이나요?

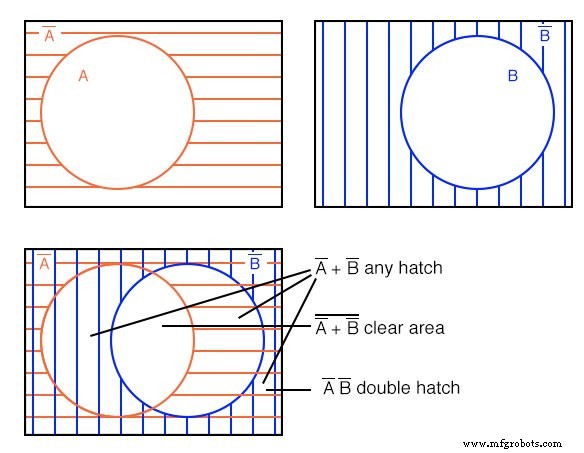
해결책: 위 그림

빨간색 수평 해치 A'로 시작 및 파란색 수직 해칭 B' 위에. 그림과 같이 도표를 겹쳐 놓습니다. 여전히 A'를 볼 수 있습니다. 다른 해치 위에 겹쳐진 빨간색 수평 해치. 또한 B (B-true) 원이지만 B의 해당 부분만 A에 일반적이지 않은 열린 원 열린 원.

B'만 보면 파란색 수직 해치, 열린 A B에게 흔하지 않은 원 . 유형에 관계없이 해치가 있는 모든 지역은 A'+B'에 해당합니다. . 즉, 중앙의 열린 여백을 제외한 모든 것입니다.

예:

부울 표현식 (A'+B')'은(는) 무엇을 의미합니까? 벤다이어그램처럼 보이나요?

해결책: 위 그림, 왼쪽 아래

중앙의 흰색 열린 공간을 보면 모든 것이 아니다 A'+B'의 이전 솔루션에서 , (A'+B')' .

예: (A'+B')' =AB임을 표시

해결책: 그림 아래, 왼쪽 아래

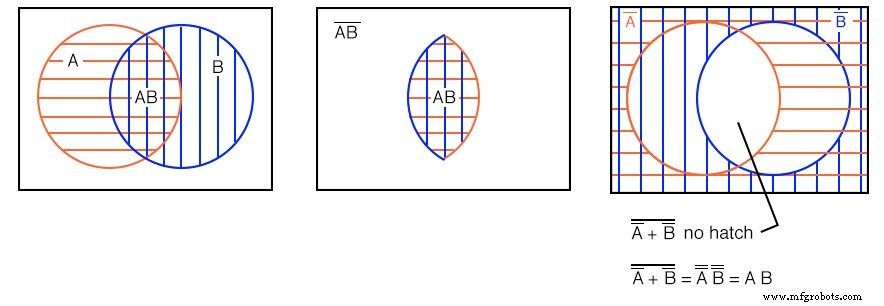
이전에 위의 오른쪽 다이어그램에서 흰색 열린 영역이 (A'+B')'임을 보여주었습니다. . 이전 예에서 우리는 AB의 교차점(오버레이)에서 이중 해치 영역을 보여주었습니다. . 여기에서 반복되는 왼쪽과 가운데 그림입니다.

두 벤 다이어그램을 비교하면 이 열린 영역이 (A'+B')' , 이중 해칭 영역 AB와 동일 (A 및 B). (A'+B')'=AB임을 증명할 수도 있습니다. DeMorgan의 정리와 위의 이중 부정에 의해.

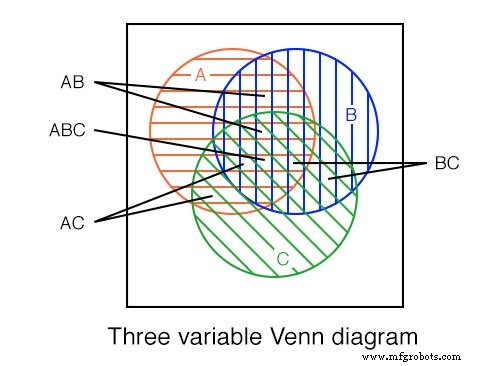
위의 A 영역과 함께 3개의 가변 벤 다이어그램을 보여줍니다. (빨간색 가로), B (파란색 세로) 및 C (녹색 45 ^o ). 가장 중앙에 있는 세 영역은 모두 부울 표현식 ABC를 나타내는 겹칩니다. .

A가 있는 더 큰 꽃잎 모양의 영역도 있습니다. 및 B 부울 표현식 AB에 해당하는 겹침 . 유사한 방식으로 A 및 C 중복 생성 부울 표현식 AC . 그리고 B 및 C 중복 생성 부울 표현식 BC .

위의 AND 표현식으로 설명된 영역의 크기를 보면 연관된 AND 표현식의 변수 수에 따라 영역 크기가 변한다는 것을 알 수 있습니다.

<울>

A , 1-변수는 큰 원형 영역입니다.

AB , 2-변수는 더 작은 꽃잎 모양 영역입니다.

ABC , 3-변수는 가장 작은 영역입니다.

AND 항에 변수가 많을수록 영역이 작아집니다.