나노물질








헤테로에피택셜 아일랜드의 측면 정렬은 증착 전에 기판의 적절한 피트 패터닝에 의해 편리하게 달성될 수 있습니다. 피트의 모양, 방향 및 크기를 제어하는 것은 준안정적이어서 증착/어닐링 중에 크게 발전할 수 있으므로 사소한 일이 아닙니다. 이 논문에서 우리는 초기 깊이/모양에 따라 Si(001)에서 예상할 수 있는 전형적인 준안정 피트 형태를 탐색하기 위해 연속체 모델을 활용합니다. 진화는 위상-장 프레임워크에서 공식화된 표면 확산 모델과 표면 에너지 이방성 문제를 사용하여 예측됩니다. 결과는 문헌에 보고된 전형적인 준안정 형태를 훌륭하게 재현하는 것으로 나타났습니다. 더욱이, 깊이가 다른 구덩이 프로파일의 오랜 시간 규모 진화는 유사한 운동 경로를 따르는 것으로 밝혀졌습니다. 이 모델은 또한 평형 Wulff 모양에서 서로 다른 면을 특징으로 하는 두 재료를 포함하는 이종 에피택시 성장의 경우를 처리하는 데 활용됩니다. 이는 Ge/Si 실험에서 입증된 바와 같이 증착 중 피트의 회전과 같은 형태에 상당한 변화를 일으킬 수 있습니다.
<섹션 데이터-제목="배경">여러 반도체(예:Ge/Si 또는 InGaAs/GaAs)의 격자 불일치 헤테로에피택시로 인해 SK(Stranski-Krastanow) 성장 모드에 따라 3D 섬이 형성될 수 있습니다. 순수한 자가 조립에 의해 이러한 점을 얻을 수 있는 가능성[1, 2]은 특히 매력적이며 광범위한 관심을 불러일으켰지만 무작위 핵 생성은 크기와 모양의 분산과 함께 응용 분야를 심각하게 방해할 수 있다는 사실을 곧 깨달았습니다.
수십 년간의 연구를 통해 이종 에피택시 성장을 정렬된 구조의 형성으로 이끄는 다양한 방법이 개발되었습니다[3-7]. 그 중, 피트 패턴 기판의 사용은 헤테로에피택시 섬의 높은 순서와 크기 제어를 모두 달성하기 위해 가장 다양한 방법 중 하나로 입증되었습니다[8-15].
피트 패턴 기판은 일반적으로 나노임프린트 리소그래피[16-18], 전자빔 리소그래피[13, 14]와 반응성 이온 에칭(RIE)[19, 20] 또는 습식 화학 에칭[21, 22] 및 nanoindentation [23, 24], 즉 하향식 접근 방식에 의한 것입니다. 이러한 방법으로 구덩이의 정렬된 패턴은 높은 정밀도로 설계되고 적절한 성장 조건[14, 25]에서 거의 완벽한 측면 정렬로 이어집니다.
구덩이의 실제 모양은 시스템의 에너지에 영향을 미치고 더 일반적으로 섬 핵 생성[26, 27]에 영향을 미치므로 구덩이의 형태를 제어하는 것이 중요합니다. 이것은 사소한 일이 아닙니다. 결국 구덩이는 기판에 뚫린 구멍일 뿐입니다. 따라서 충분히 높은 온도에서 모세관 현상[28]은 형태학적 진화를 일으켜 결국 완전한 치유로 이어질 것으로 예상됩니다. 실제로, 초기 피트 형성 이후의 어닐링 공정 또는 기판 재료의 추가 증착은 재현 가능하고 수명이 긴 준안정 형상을 달성하기 위해 종종 사용됩니다[8, 26]. 구덩이가 모양이 안정화된 후에도 실제 이종 에피택시 동안 추가 진화가 이루어질 수 있다는 점에 유의하십시오[29, 30].
이 작업에서 우리는 표면 확산을 통한 표면 에너지 감소에 의해 구동되는 피트 패턴 기판의 진화를 설명하는 것을 목표로 합니다. 우리는 적절한 위상장 접근법[31]을 채택하여 실험적인 것과 호환되는 길이 및 시간 규모의 시뮬레이션을 허용합니다[32]. 이 모델은 헤테로에피택시 시스템에서 형태학적 진화 동안 확산 제한 동역학을 설명하기 위해 이미 채택되었습니다[33-36]. 또한 실제적인 이방성 표면 에너지를 포함하여 평형을 향한 진화를 적절하게 설명하는 것으로 나타났습니다[37-39].
일반성을 잃지 않고 문헌[8, 10, 14, 30, 40, 41]에서 널리 조사된 피트 패턴의 Si(001) 표면 관련 사례에 초점을 맞출 것입니다.
작업은 다음과 같이 구성됩니다. "위상-장 모델" 섹션에서는 이방성 표면 에너지를 포함하는 표면 확산에 의한 진화를 설명하는 데 사용되는 위상-장 모델을 간략하게 설명합니다. 또한 실제 Si Wulff 모양이 고려된 접근 방식에서 설명되는 방법을 설명합니다. "Si(001) 구덩이의 평활화" 섹션에서는 표면 에너지 감소에 의해 구동되는 Si(001) 구덩이의 예상 평활화에 대해 다양한 초기 구성을 고려하여 평형을 향한 운동 경로의 개요를 설명합니다. "Ge Overgrowth로 인한 형상 변화 모방" 섹션에서는 Si 피트에 Ge의 얇은 층을 증착할 때 표면 에너지 구동 형상 변화에 해당하는 헤테로에피택시 성장의 특정 경우에 이 방법을 적용하는 것을 고려합니다. 결론 및 발언은 "결론" 섹션에 요약되어 있습니다.
위상 필드 모델은 연속 차수 매개변수 φ를 고려합니다. , φ 사이에서 다양 =1(솔리드) 및 φ =0(진공) [31, 32]. 접근 방식은 에너지 기능 [37],
$$ \begin{aligned} F=&\int_{\Omega} \gamma(\hat{\mathbf{n}}) \left(\frac{\epsilon}{2} |\nabla \varphi|^{2 } + \frac{1}{\epsilon}B(\varphi) \right) d\mathbf{r} + \\ &+\int_{\Omega} \frac{\beta}{2\epsilon} \left( -\epsilon\nabla^{2}\varphi+\frac{1}{\epsilon}B'(\varphi)\right)^{2} d\mathbf{r}, \end{정렬} $$ (1)\(\Omega \in \mathbb {R}^{3}\) φ 정의 영역 (r ) 및 r =(x ,y ,z ). 첫 번째 항은 φ로 정의된 확산 계면 영역 내 위상 간의 계면 에너지에 해당합니다. , 즉, 고체상의 표면 에너지. \(\gamma (\hat {\mathbf {n}})\)는 표면 에너지 밀도이며 \(\hat {\mathbf {n}}\) 바깥쪽을 가리키는 표면 법선, ε 위상 사이의 경계면의 두께. 나 (φ )=18φ 2 (1−φ ) 2 φ의 최소값을 갖는 이중 우물 포텐셜입니다. =0 및 φ =1 참조에서와 같이. [31]. 식의 두 번째 항. (1)은 날카로운 모서리의 형성을 피하기 위해 강한 이방성 영역에서 필요한 Willmore 정규화입니다[37, 38, 42]. β 모서리 라운딩에 해당하는 매개변수입니다.
φ의 진화 표면의 확산 제한 역학을 재생산하고 축퇴 Cahn-Hilliard 모델, 즉
에 의해 제공됩니다. $$ \frac{\partial \varphi}{\partial t}=D \nabla \left[ M(\varphi) \nabla \mu \right], $$ (2)여기서 μ =δ F /δ φ 는 화학적 잠재력, D 는 확산 계수이고 M (φ )=(36/ε )φ 2 (1−φ ) 2 는 표면에 제한된 이동성 함수입니다. μ에 대한 방정식 읽기
$$ \begin{aligned} g(\varphi)\mu =\delta F/ \delta \varphi=&-\epsilon \nabla \cdot \left[\gamma(\hat{\mathbf{n}}) \nabla \varphi \right] + \frac{1}{\epsilon} \gamma(\hat{\mathbf{n}}) B'(\varphi) + \\&-\epsilon \nabla \cdot \left[|\ nabla \varphi|^{2} \nabla_{\nabla \varphi} \gamma(\hat{\mathbf{n}}) \right] + \\ &+\beta\left(-\nabla^{2} \ 카파 + \frac{1}{\epsilon^{2}} B^{\prime\prime}(\varphi) \kappa \right), \end{정렬} $$ (3)κ와 함께 =−ε ∇ 2 φ +(1/ε )나 ′ (φ ) 및 g (φ )=30φ 2 (1−φ ) 2 [33, 37, 38]. 후자는 표면 확산을 통한 물질 수송의 설명에 영향을 미치지 않으면서 계면 두께의 2차 수렴을 보장하는 안정화 기능입니다[43, 44]. 평형 상태에서 계면에 수직인 방향의 프로파일은
로 잘 설명됩니다. $$ \varphi(\mathbf{r})=\frac{1}{2}\left[1-\tanh \left(\frac{3 d(\mathbf{r})}{\epsilon} \right) \오른쪽], $$ (4)여기서 d (r )은 위상 간 인터페이스 중심까지의 부호 있는 거리입니다. 이 방정식은 φ의 초기 조건을 설정하기 위해 채택됩니다. 다음에 명시된 대로. 고체상의 표면을 φ라고 합니다. ~0.5 등가면. 고려된 표면의 모든 기하학적 속성은 φ에서 파생될 수 있습니다. , 예를 들어 바깥쪽을 가리키는 표면 법선 \(\hat {\mathbf {n}}=- \nabla \varphi / | \nabla \varphi |\).
이방성 표면 에너지를 설명하기 위해 [38, 39]에 소개된 것처럼 표면 에너지 밀도 \(\gamma (\hat {\mathbf {n}})\)의 정의를 고려했습니다.
$$ \gamma(\hat{\mathbf{n}})=\gamma_{0} \left(1-\sum_{i}^{N} \alpha_{i} \left(\hat{\mathbf{n }} \cdot \hat{\mathbf{m}}_{i} \right)^{w_{i}} \Theta\left(\hat{\mathbf{n}} \cdot \hat{\mathbf{m }}_{i}\right) \right). $$ (5)여기서 우선적인 방향 \(\hat {\mathbf {m}}_{i}\), 즉 표면 에너지 밀도가 최소가 되는 방향은 상대 깊이에 따라 임의로 설정할 수 있습니다. α 나 , γ에 대해 0 . 매개변수 w 나 m 주변의 \(\gamma (\hat {\mathbf {n}})<\gamma _{0}\) 영역의 확장을 제어합니다. 나 방향, 즉 최소값의 너비입니다(참고문헌 [38] 참조).
Si 결정의 특정 등방성을 설명하기 위해 최소 에너지 방향을 설정합니다. m 나 , 〈001〉, 〈113〉, 〈110〉, 〈111〉[45]에 해당합니다. α 나 최소값의 깊이를 결정하는 계수는 [39]
$$ \alpha_{i}=1-\left(\frac{\gamma_{i}}{\gamma_{\langle 001\rangle}}\right)\left(1-\alpha_{\langle 001 \rangle} \오른쪽), $$ (6)여기서 α 〈001〉 =0.15가 기준으로 설정되고 다양한 γ 나 Ref.에 보고된 앞서 언급한 방향의 표면 에너지 값에 해당합니다. [45]. 일반성을 잃지 않고 γ를 설정합니다. 0 =1. 실제로 최소값과 이방성 강도의 비율은 α 나 식의 값 (6) 및 α 〈001〉 , 동안 γ 0 Eq.에서 prefactor의 역할을 한다. (2) 따라서 진화의 절대 시간 척도에만 영향을 미칩니다.
Eq.에서 에너지 최소값의 너비. (5) w로 설정 나 w를 제외한 모든 최소 방향에 대해 =50 〈113〉 =100 [39]. 이 매개변수 정의에 따르면 날카로운 모서리는 Wulff 모양으로 예측됩니다. 즉, 표면 에너지 이방성이 "강하다"[38, 42, 46]. 따라서 시뮬레이션을 수행하려면 Willmore 정규화가 엄격하게 필요합니다. β 값은 반경이 \(\sqrt {\beta }\) [37]에 비례하는 것으로 알려진 모서리에서 둥근 영역의 확장을 설정합니다. 시뮬레이션을 수행하기 위해 모서리에서 라운딩에 의해 설정된 길이 스케일은 β 수치적 방법의 공간 이산화의 분해능보다 커야 합니다. 그러나 \(\sqrt {\beta }\) 순서로 확장된 Wulff 모양에 존재할 수 있는 작은 패싯은 너무 큰 β를 사용할 때 숨겨질 수 있다는 점을 언급할 가치가 있습니다. Wulff 모양에 실제로 존재하는 우선 순위와 관련된 소규모 패싯뿐만 아니라 값도 포함됩니다. 이 작업에서는 β를 설정합니다. =0.005. 시뮬레이션 영역의 크기에 따라 다음과 같이 지정되며 이 값을 통해 실현 가능한 공간 이산화를 채택할 수 있습니다. 또한, Eq.에 들어가는 모든 우대 오리엔테이션. (5)와 (6)이 재현됩니다. 반면에 ~0.07보다 작은 스케일과 관련된 가능한 패싯은 모서리 라운딩의 확장으로 인해 재현할 수 없습니다.
이 절에서 정의한 위상장 모델에 의한 형태학적 진화를 조사하기 위해 φ에 대한 적절한 초기 조건 설정해야 합니다. 우리는 여기에서 참조 프레임이 \(\hat {\mathbf {x}}=\,[\!100]\), \(\hat {\로 설정된 (001) 평면 표면에 새겨진 부드러운 구덩이 기하학을 고려합니다. mathbf {y}}=\,[\!010]\) 및 \(\hat {\mathbf {z}}=\,[\!001]\). 특히 반지름이 L인 원형(001) 표면을 고려합니다. 높이 h에서 0 -안 , 높이 h에서 주변 (001) 평면 표면에 매끄럽게 연결됨 0 . 이러한 기하학은 φ에 대한 초기 조건으로 설정됩니다. 식을 이용하여 (4) d (r ) 표면에서 서명된 거리 Γ (x ,y )
에 의해 정의됨 $$ \Gamma(x,y)=\left\{ \begin{aligned}h_{0} - &H &\qquad r \leq L \\ h_{0} - &H \exp \left[ -\frac {1}{2}\frac{|\mathbf{s}-\bar{\mathbf{s}}|^{2}}{\sigma^{2}} \right] &\qquad r> L \end {정렬} \오른쪽. $$ (7)\(r=\sqrt {x^{2}+y^{2}}\) 및
$$ \mathbf{s}=(x,y), \qquad \bar{\mathbf{s}} =\frac{R}{r} (x,y). $$ (8)R =안 /4L 는 종횡비 매개변수로 정의되는 반면 σ 는 피트 바닥과 피트 주변의 평평한 영역 사이의 연속 연결 확장을 제어하는 매개변수입니다. 이 매개변수는 여기에서 σ로 설정됩니다. =엘 /2.
그림 1에서 φ에 대한 초기 조건은 가 예시되어 있습니다. 그림 1a는 Γ를 보여줍니다. (x ,0) R 값이 다른 프로필 . 그림 1b는 φ의 정의를 보여줍니다. 식을 통해 (4) 3D 평행육면체 영역에서. 특히 이 패널은 전체 영역의 중심을 통과하는 단면을 보여줍니다. 왼쪽 부분은 고체상에 해당하는 영역, 즉 φ인 영역을 나타냅니다.>0.5, 초기 구덩이 형태에 해당하는 표면을 나타냅니다. 오른쪽 부분은 φ의 값을 나타냅니다. 전체 3D 영역, 즉 벌크 단계와 이들 사이의 지속적인 전환 내에서.
<그림>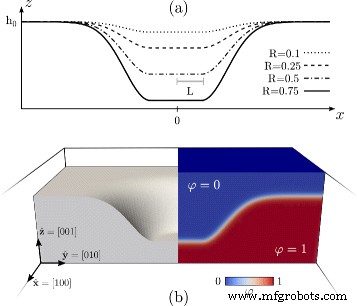
고체 필름의 (001) 표면에 있는 매끄러운 구덩이와 유사한 위상장 모델의 초기 조건입니다. 아 Γ (x ,0) 식의 프로파일. (7) 다른 R에 대해 획득 가치. ㄴ φ의 정의 수치 시뮬레이션을 위해 채택된 3D 영역에서. 방정식에서 얻습니다. (4) d (r ) Γ에서 서명된 거리 (x ,y ) R =0.5. 왼쪽에서 φ인 고체상> 0.5가 표시됩니다. 오른쪽은 φ를 나타내는 컬러맵입니다. 3D 도메인에서 보고됨
Eqs를 통합하기 위해 수치 시뮬레이션이 수행됩니다. (2) 및 (3). 이는 유한 요소 방법(FEM) 도구 상자 AMDiS[47, 48]를 사용하여 수행되며 인터페이스에서 반 암시적 통합 방식 및 메쉬 미세 조정[33, 38, 49]을 사용합니다. 주기적인 경계 조건은 \(\hat {\mathbf {x}}\) 및 \(\hat {\mathbf {y}}\) 방향으로 설정됩니다. 무플럭스(Neumann) 경계 조건은 \(\hat {\mathbf {z}}\) 방향을 따라 시뮬레이션 도메인의 상단과 하단에 설정됩니다. 진화의 시간 척도는 계수 1/D로 조정됩니다. , 세트 D에 해당 =1. 다음에서는 임의의 단위로 시뮬레이션 시간을 참조합니다. 구덩이의 크기는 임의로 L로 설정 =1, 인터페이스 두께가 ε로 설정된 동안 =0.2.
이 섹션에서는 피트 패턴 Si(001) 기판의 진화 동안 형태학적 변화에 관한 결과를 설명합니다. 위에 설명된 모델은 "이방성 표면 에너지" 섹션에서와 같이 이방성 표면 에너지의 정의를 통해 실리콘의 특정 경우에 대한 설명을 허용합니다. 시스템이 연속체 접근법(\(\gtrsim 10\) nm) [32]을 채택하기에 충분히 크고 모양이 종횡비 R 도 1a와 유사하다. 실제 길이 척도는 L을 설정하여 고려할 수 있습니다. 실제 단위로 해당 매개변수, L r . 실시간 척도는 D의 실제 값을 고려하여 설명할 수 있습니다. 및 γ 0 L 곱하기 r 길이, 즉 L 크기 조정 r /엘 L 위에 명시된 대로 단일.
먼저 진화의 첫 단계에 초점을 맞추자. Eq.에 의해 설정된 초기 조건. (7) 표면의 우선적인 방향을 나타내지 않는 프로파일로 구성됩니다. 이방성 표면 에너지의 감소로 인한 표면 확산에 의한 진화를 고려할 때 초기 프로파일의 패싯이 예상됩니다. 이것은 R이 있는 두 프로필의 패싯이 그림 2에 나와 있습니다. =0.25(그림 2a 및 R) 도 2b의 =0.5가 보고된다. 색상 척도는 표면의 \(\gamma (\hat {\mathbf {n}})\) 값을 보여줍니다. 이를 통해 패싯을 식의 최소값에 해당하는 거의 균일한 표면 에너지 밀도를 가진 영역으로 식별할 수 있습니다. (5) \(\gamma (\hat {\mathbf {n}})\) 값이 높은 지역화된 영역으로 경계를 이룹니다. 구덩이의 초기 종횡비에 따라 다른 면이 형성됩니다. 더 작은 R의 경우 하단의 (001) 면은 정사각형 모양을 가정하여 유지됩니다. 작은 삼각형 모양의 면으로 연결된 4개의 면으로 둘러싸인 구덩이의 가장자리가 나타납니다. 더 큰 종횡비에 따라 R을 고려할 때 더 큰 패싯 표면이 존재합니다. =0.5, (001) 표면에 대해 더 높은 기울기로 우선적인 방향의 모양을 허용합니다. 특히 초기 모양은 바닥과 평평한 영역에 가까운 두 개의 패싯 사이에 형성되는 패싯의 존재를 허용합니다. 그 사이에 넓은 면이 형성됩니다.
<그림>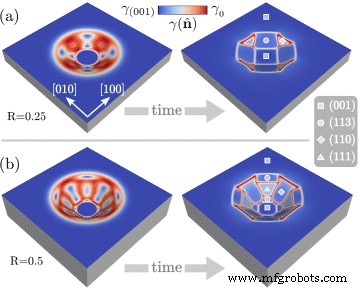
Si의 표면 에너지를 재현하는 표면 확산 및 \(\gamma (\hat {\mathbf {n}})\)에 따른 "초기 형태 및 시뮬레이션 설정" 섹션에 정의된 초기 프로파일의 패싯. 두 가지 다른 초기 형태가 고려됩니다. a R =0.25 및 b R =0.5. 패싯 형태에서 패싯 패밀리를 식별하기 위해 기호가 채택됩니다. 색상 스케일은 표면의 \(\gamma (\hat {\mathbf {n}})\) 값을 보여줍니다.
그림 2에 보고된 결과는 종횡비에 따라 또는 일반적으로 초기 형태에 따라 패싯 피트 형태를 예측할 가능성을 보여줍니다. 우리는 이제 평형까지의 형태학적 진화를 검사하는 긴 시간 규모 역학도 조사합니다[38]. 이것은 우리가 지금까지 고려한 가장 깊은 구덩이에 초점을 맞춘 그림 3에 나와 있습니다. 즉, R =0.5이고 주요 형태적 변화가 표시됩니다. 특히, 진화 동안 얻은 다양한 형태의 투시도와 평면도가 각각 그림 3a, b에 보고되어 있습니다. 이 시뮬레이션의 첫 번째 단계에서 가장 가파른 면이 사라지고 인접한 {113} 면이 확대되는 것을 관찰합니다. 그런 다음 후자가 병합되고 패싯 축소가 시작됩니다. 이들은 삼각형 모양을 가정한 후 나중 단계에서 사라지는 것으로 밝혀져 평면도에서 구덩이에 정사각형 윤곽선을 제공합니다. 또한 {113} 패싯은 결국 사라지고 전역 평면화가 이루어집니다. 이 시뮬레이션에서 얻은 실시간 규모는 문헌의 데이터로 추정할 수 있습니다. 특히 D를 고려할 수 있습니다. Arrhenius 법칙에 의해 결정되며 Ref. [50], 열 변동도 설명됩니다. γ 0 \(\gamma (\hat {\mathbf {n}})\sim 8.7\) eV/nm 2 식에서 \(\hat {\mathbf {n}}=(001)\) [51]일 때 (5) 즉, γ 0 =10.2 eV/nm 2 . 표면 확산의 다른 재료 의존 계수[28], 즉 표면에서의 원자 부피 및 밀도는 Si의 경우를 재현하도록 설정됩니다. 이 값에 따르면 L의 경우 고온 T ~1100-1200 °C에서 전체 공정의 예상 지속 시간 r 수십 나노미터는 몇 시간 정도입니다.
<사진>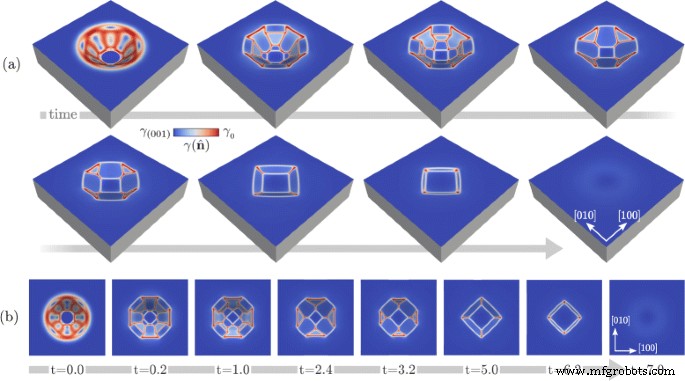
그림 2b와 같은 초기 형태를 갖는 Si 피트의 평형을 향한 진화. 아 주요 형태학적 변화를 보여주는 투시도. ㄴ 패널 a에 있는 형태의 평면도 . 패널 b에 보고된 시간 임의의 단위로 표시됩니다. 색상 스케일은 표면의 \(\gamma (\hat {\mathbf {n}})\) 값을 보여줍니다.
진화 과정에서 발생하는 특정한 형태적 변화와 함께 두 가지 주요 특징에 주목해야 합니다. 첫째, 진화는 표면의 예상되는 전지구적 평탄화로 이어지며, 이것은 가파른 면이 더 얕은 면으로 대체되면서 점진적으로 사라지면서 발생합니다. 이 동작은 에너지 최소화 및 종횡비 낮추기에 대한 주장으로 추론할 수 있지만, 여기에는 유사한 패싯의 존재를 다루지만 상대적 크기가 다른 전체 발전이 제공된다는 점을 지적할 가치가 있습니다. 이것은 진화 중에 얻은 형태가 평형을 벗어난 구성에 해당하고 지구 에너지 최소값을 향한 경로를 정의한다는 사실과 일치합니다. 그런 다음 예상되는 측면과 에너지가 알려져 있음에도 불구하고 진화의 특정 지점에서의 특정 형태는 전 지구적 에너지 최소화를 고려하는 것이 아니라 역학을 설명해야만 설명할 수 있습니다[38].
그림 3에 보고된 결과에 의해 나타난 두 번째 중요한 점은 중간 단계에 관한 것이다. 진화 중 형상이 R로 얻은 초기 프로파일과 유사한 깊이를 갖는 기하학에 접근할 때 =0.25, 즉, t에서 ~3.2, 에너지 최소화에 의해 유도된 형태는 깊이의 상당한 차이(이 경우 두 배)가 있는 초기 구성에서 시작할 때에도 그림 2b에 보고된 것과 매우 유사합니다. 이것은 초기 형태의 첫 번째 빠른 패싯 후에 도달하는 최종 평탄화를 향한 공통 운동 경로의 존재를 시사합니다. 이 주장은 실제로 확인되었으며 그림 4의 플롯에 추가로 설명되어 있습니다. 여기에서 R이 있는 구덩이를 고려할 때 초기 패싯 후 진화 중 단조로운 에너지 감쇠가 보고됩니다. 그림 1a에서와 같이 0.1, 0.25, 0.5 및 0.75와 같습니다. 도 4a에서는 임의의 단위로 표현된 시간 척도가 고려된다. 그림 4b에서 시간 척도의 적절한 이동과 함께 동일한 에너지 변화가 보고되었으며 구조의 유사한 종횡비에 접근할 때 유사한 에너지 감쇠가 강조 표시됩니다. \(t^{*}_{R}\) 는 평면 표면을 얻는 시간, 즉 전체 에너지 최소값에 도달하는 시간으로 정의되며, 이는 그림 1과 같이 시뮬레이션마다 다릅니다. 4 가. 이 플롯에서 볼 수 있듯이 에너지 감쇠는 R에 대해 거의 겹칩니다. ≤0.5. R을 고려할 때만 아주 작은 차이가 관찰됩니다. =0.75, 에너지 감쇠 결과는 여전히 다른 곡선에 매우 가깝고 차이는 기본적으로 \(t \gtrsim 5.0\)에서 사라집니다. 초기 구성, 즉 R과의 큰 편차에 대해 언급할 가치가 있습니다. ≫1, 그러한 기하학은 시간 규모와 형태에 다른 영향으로 다르게 진화할 수 있습니다[52, 53]. 더욱이, 위상 변화는 예를 들어 매우 깊은 해구와 같은 극단적인 경우에 발생하는 것으로 알려져 있어 평평한 (001) 표면이 있는 전체 평형에 도달할 가능성을 방지합니다[34, 39, 54].
<그림>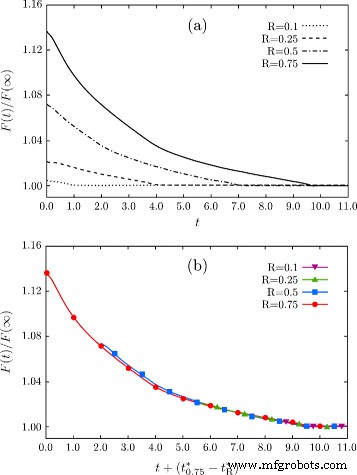
피트 형상이 진화하는 동안 에너지가 감소합니다. 아 F (그 ) 진화의 마지막 단계로 얻은 평평한 (001) 표면의 에너지에 의해 정규화됩니다. 다른 R을 갖는 시뮬레이션에서 얻은 에너지 감쇠 초기 프로필, 즉 R에서 =0.1 ~ R =0.75가 표시됩니다. 시간은 임의의 단위로 표시됩니다. ㄴ 패널 a의 곡선 \(t_{R}^{*}\), 즉 R에 따라 구덩이가 전체적으로 평평해지는 시간과 일치하도록 이동
이 섹션에 보고된 시뮬레이션에서 얻은 모양은 특히 열역학적 한계에 가까운 조건을 포함하는 처리가 포함된 경우 실험에서 관찰될 것으로 예상됩니다. 그림 3에 보고된 일부 형태는 실제로 피트 패턴 Si(001) 기판의 윤곽과 일치합니다. 예를 들어, t에서 그림 3과 같이 좁은 {113} 면으로 둘러싸인 넓은 (001) 표면으로 구성된 형태 종횡비가 0.05<R인 피트 패턴 Si(001) 기판을 고려할 때 ~5.0이 관찰됩니다. Ref.에서와 같이 <0.1 [10, 30]. 또한, Fig. 3의 시뮬레이션의 앞서 언급한 단계에서 패싯의 상대적 확장은 이러한 실험 작업에서 보고된 것과 매우 유사합니다. 시뮬레이션과 실험 간의 이러한 일치는 여기에서 채택된 표면 확산에 대한 이론적 설명을 추가로 평가합니다. 그러나 우리는 프로세스의 일반적인 특징에 초점을 두었고 특정 실험에 대한 더 자세한 비교는 본 작업의 목적을 벗어났습니다.
서론에서 언급했듯이 피트 패턴 Si 템플릿의 주요 응용 중 하나는 자체 조립된 섬의 성장을 제어하는 것입니다[55]. 이것은 Ge 또는 Si1 − c의 위치를 고려할 때 특히 사실입니다. Ge c Si(001) 기판의 섬 [6]. 이전 섹션에서 채택한 방법론을 사용하여 표면 에너지의 특성과 관련된 형태학적 변화를 조사할 수 있습니다. 따라서 Si 피트의 실제 형태와 유사한 적절한 초기 구성에서 시작하고 다른 재료를 증착할 때 예상되는 표면 에너지 밀도의 차이를 고려하여 형태 변화에 대한 해당 기여를 예측할 수 있습니다.
사례 연구는 여기에서 종횡비가 0.1에 가까운 Si(001) 피트 패턴 기판 위에 Ge의 과성장으로 구성됩니다. t에서의 도 3의 프로파일 =5.0은 초기 형태로 간주됩니다. 그런 다음, 〈105〉 방향을 따라 최소값도 포함하는 표면 에너지가 설정됩니다. \(\gamma (\hat {\mathbf {n}})\) 의 정의는 Ge/Si(001) 시스템에서 가장 선호하는 작은 기울기의 존재를 모방합니다[56–58]. {105} 패싯의 높은 안정성은 표면 재구성과 에피층과 기판 사이의 격자 불일치와 관련된 변형 효과 간의 상호작용 때문입니다[59-61]. 식에서 사용되어야 하는 표면 에너지 밀도 값. (6) Ref. 두꺼운 Ge 층의 한계에서. {1 1 10}과 같이 (001)에 더 가까운 표면 에너지를 갖는 다른 패싯은 여기에서 무시됩니다. 〈105〉와 [001] 방향 사이의 각도가 매우 작기 때문에 w 나 이전에 채택된 것보다 큰 매개변수는 Eq의 에너지 최소값을 적절하게 설명하는 데 필요합니다. (5) [38]. 특히 w {105} =와 {001} =500.
그림 5에서 \(\gamma (\hat {\mathbf {n}})\) 의 새로운 정의로 표면 확산에 의한 진화가 보고되었습니다. 그림 5a는 z 배율로 표면의 형태학적 진화를 보여줍니다. -axis by factor 5. 첫 번째 단계에서는 초기 프로필에 있는 패싯 사이에 패싯이 형성됩니다. 〈105〉 방향은 그림 5b와 같이 최소 에너지를 가지므로 해당 패싯은 확장되고 {113} 패싯은 축소됩니다. 나중 단계에서 패싯으로 둘러싸인 구덩이는 바닥에 여전히 (001) 표면으로만 형성됩니다. 그림 5b와 같은 평면도에서 형태의 변화는 Pit의 외곽선을 45° 회전시키는 결과를 낳습니다. 이것은 실제로 실험[41]에서 Si 패턴 기판에 Ge를 증착하는 동안이나 결함이나 불순물로 인한 피트의 자발적인 성장[40] 중에 관찰됩니다. {105} 패싯의 형성은 또한 Ge 점의 추가 성장을 위해 선호하는 핵 생성 사이트 역할을 하는 것으로 밝혀졌습니다[30]. 그림 5에 설명된 진화는 표면 에너지 감소로 인해 피트 윤곽의 회전으로 이어지는 모양의 변화가 달성될 수 있음을 보여줍니다. 이것은 열역학적 추진력이 표면 기여에 의해 지배되는 평형에 가까운 조건, 즉 작은 Ge 부피의 실제 상황으로 예상됩니다. 실제로 이 과정을 완전히 설명하기 위해서는 탄성효과, 혼합, 고체상의 성장이 포함되어야 한다[32]. {11n을 따라 법선이 있는 면을 보여주는 실험에서 더 얕은 Si 피트가 채택되었다는 점도 언급할 가치가 있습니다. } 방향, 5<n <10 [41](즉, {1 1 10} 패싯). 이 패싯으로 둘러싸인 구덩이 형상은 (001) 평면에 대해 더 작은 기울기를 가진 그림 4의 초기 구성으로 채택된 것과 일치하므로 유사한 발전으로 이어질 것입니다.
<그림>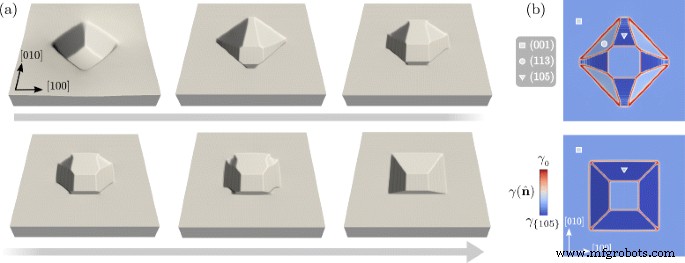
t에서 그림 3의 프로파일 진화 =5.0, 〈105〉 방향을 포함하는 표면 에너지의 정의. 아 패싯으로만 경계를 이루는 구덩이 형성을 향한 진화의 대표적인 단계에서의 표면 프로필입니다. z -축이 5배 확대됩니다. b 표면에서 \(\gamma (\hat {\mathbf {n}})\) 값을 보여주는 평면도. 패널 a의 두 번째 및 마지막 단계 상단과 하단에 각각 보고됩니다. 다양한 패싯 패밀리를 식별하기 위해 그림 2와 같은 기호가 채택되었습니다.
이 작업에서 우리는 Si(001) 기판에서 발굴된 구덩이의 시간적 진화를 조사하기 위해 표면 확산을 기반으로 하는 연속체 모델을 사용했습니다. 잘 알려진 Si Wulff의 모양을 기반으로 한 매개변수화를 사용하여 (강한) 표면 에너지 이방성을 적절하게 해결함으로써, 우리는 다른 재료의 증착이 새로운 안정적인 면을 도입하는 경우를 포함하여 실험과 일치하는 전형적인 준안정 구성을 예측했습니다. The entire evolution towards the global flattening of the pit has been illustrated, and it is found to follow the same kinetic pathway also when considering pits with different initial depths. We believe that the model can be predictive also for initial configurations strongly deviating from the ones which we have analyzed as examples. As a consequence, the present approach can be useful in designing experiments based on still-unexplored pit shapes. Furthermore, the model is general and can be easily adapted to different substrates upon re-parametrizing the surface energy.
나노물질
초록 1차원 Ag 나노구조 기반 네트워크는 차세대 투명 전도성 물질로 주목받고 있다. 높은 종횡비의 Ag 나노섬유(NF)는 침투에 필요한 수 밀도를 감소시킵니다. 따라서 질적으로 우수한 투명 전도성 필름을 형성합니다. 이 연구는 Pt 나노입자 보조 H2를 통해 Ag NF를 빠르게 제조하는 새로운 방법을 보고합니다. -고상 AgNO3의 자유로운 환원 . 우리의 결과는 먼저 폴리머가 Pt 나노 입자의 존재 하에서 수소 가스의 소스가 될 수 있음을 나타냅니다. 종횡비가 105 이상인 Ag NF AgNO3를 가열하여 여기에서 얻었습니다.
비용 절감에서 효율성 증대, 혁신 촉진에 이르기까지 많은 사람들이 3D 프린팅이 제조의 미래에 미칠 영향에 대해 기대하고 있습니다. 그러나 사실은 이미 업계에 상당한 영향을 미쳤습니다. 3D 프린팅의 발전 과정을 되돌아보고 이 현상이 어떻게 시작되었고 제조 산업이 발전하는 데 어떻게 도움이 되었는지 알아보세요. 1980년대:3D 인쇄의 기초 설정 3D 프린팅은 1980년대의 아이디어였습니다. 1981년 일본 나고야 시 산업 연구소의 Hideo Kodama는 3D 제품을 만들기 위해 재료 층을 인쇄하는 방법을 발견했습니다.