합계 및 곱 표기법

참고로 이 섹션에서는 Karnaugh 맵에 할당된 최소 항과 최대 항을 설명하기 위해 일부 텍스트에서 사용되는 용어를 소개합니다. 그렇지 않으면 여기에 새로운 자료가 없습니다.

Minterms 용어

Σ(시그마)는 합을 나타내고 소문자 "m"은 최소항을 나타냅니다. Σm은 최소항의 합을 나타냅니다. 우리의 요점을 설명하기 위해 다음 예를 다시 살펴보겠습니다. 단순화되지 않은 논리에 대한 부울 방정식 설명 ​​대신 최소항을 나열합니다.

f(A,B,C,D) =Σm(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15) 또는 f(A,B,C,D) =Σ(m1 ,m2 ,m3 ,m4 ,m5 ,m7 ,m8 ,m9 ,m11 ,m12 ,m13 ,m15 ) 

숫자는 오른쪽 아래 표시된 대로 Karnaugh 지도 내에서 셀 위치 또는 주소를 나타냅니다. 이것은 확실히 K-map에서 minterms 또는 cell의 목록을 설명하는 간결한 수단입니다.

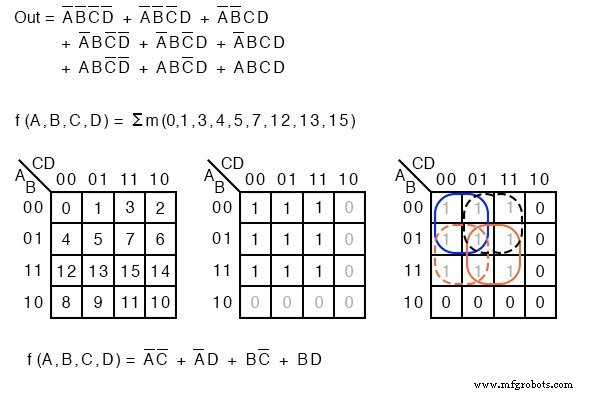
Sum-Of-Products 솔루션은 새 용어의 영향을 받지 않습니다. 최소 시험, 1 s, 지도에서 평소와 같이 그룹화되고 Sum-OF-Products 솔루션이 작성되었습니다.

Maxterms 용어

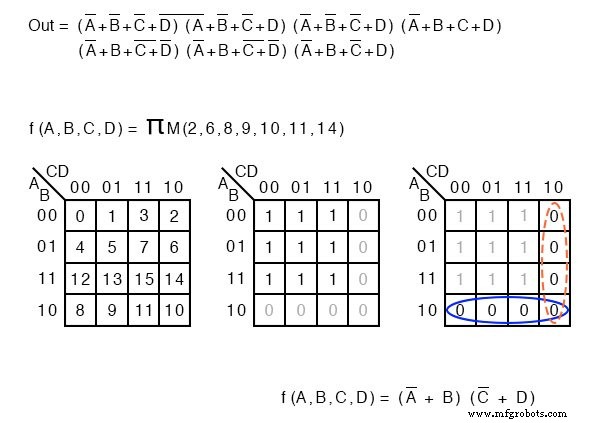
아래에서는 maxterms의 목록을 설명하는 용어를 보여줍니다. 제품은 그리스어 Π(pi)로 표시되며 대문자 "M"은 maxterms를 나타냅니다. ΠM은 최대항의 곱을 나타냅니다. 같은 예가 우리의 요점을 보여줍니다.

단순화되지 않은 논리의 부울 방정식 설명은 maxterms 목록으로 대체됩니다.

<사전>f(A,B,C,D) =Π M(2, 6, 8, 9, 10, 11, 14) 또는 f(A,B,C,D) =Π(M₂ , M₆ , M₈ , M₉ , M₁₀ , M₁₁ , M₁₄ )

다시 한 번, 숫자는 K-맵 셀 주소 위치를 나타냅니다. maxterms의 경우 이것은 0의 위치입니다. s, 아래와 같이. Product-OF-Sum 솔루션은 일반적인 방식으로 완료됩니다.

$$Out =(A + B + \bar{C} + D)(A + \bar{B} + \bar{C} + D) + (\bar{A} + B + C + \bar{D }) + (\bar{A} + B + \bar{C} + D)$$

$$(\bar{A} + B + \bar{C} +\bar{D})(\bar{A} + \bar{B} + \bar{C} + D)$$

관련 워크시트:

<울>

Sum-of-Products 및 Product-of-Sums 표현식 워크시트

Karnaugh 매핑 워크시트

부울 대수학 워크시트