복소수의 극좌표 및 직사각형 표기법

벡터를 그리지 않고 복소수를 사용하려면 먼저 일종의 표준 수학 표기법이 필요합니다. 복소수 표기법에는 두 가지 기본 형식이 있습니다. 극좌표 및 직사각형 .

복소수의 극형

극형은 복소수가 길이로 표시되는 곳입니다. (또는 크기라고도 함 , 절대값 , 또는 계수 ) 및 각도 (일반적으로 다음과 같은 각도 기호로 표시됨:∠).

지도 비유를 사용하려면 뉴욕시에서 샌디에고까지의 벡터에 대한 극 표기법은 "남서쪽으로 2400마일"과 같습니다. 다음은 벡터와 극좌표 표기법의 두 가지 예입니다.

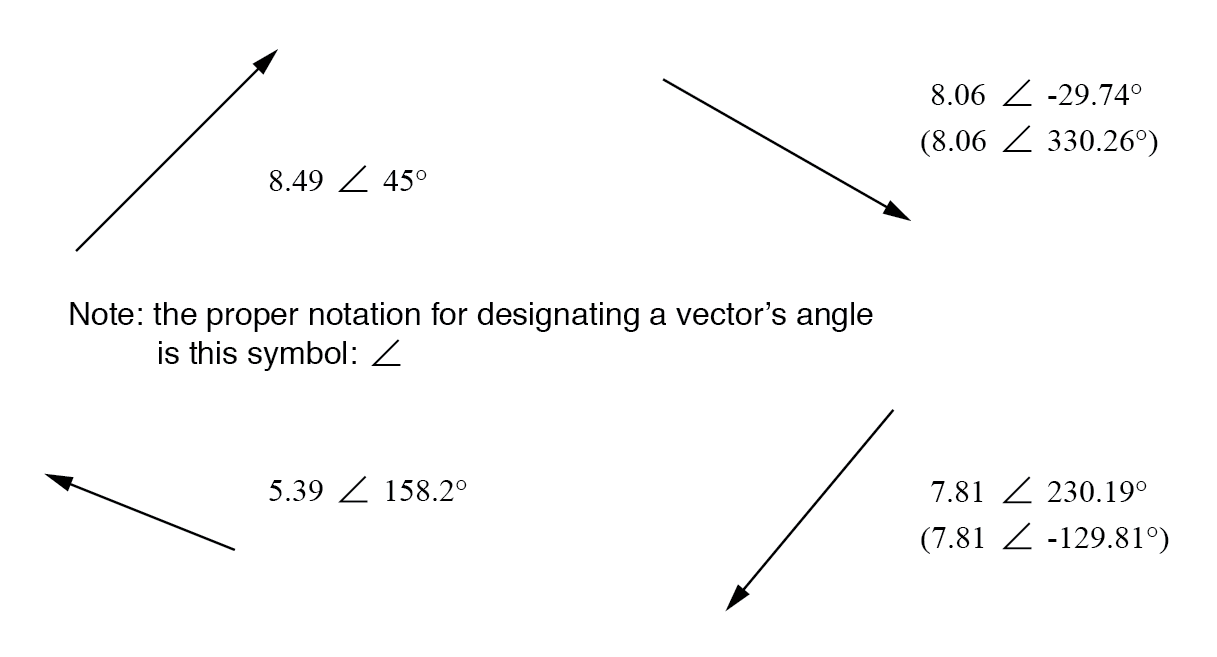
극좌표 표기법이 있는 벡터.

AC 회로 계산에서 벡터 각도에 대한 표준 방향은 0°를 오른쪽(수평)으로 정의하여 직선으로 90°, 왼쪽으로 180°, 아래쪽으로 270°를 만듭니다. "아래로" 기울어진 벡터는 180을 초과하는 양수 또는 180보다 작은 음수로 극 형식으로 표현되는 각도를 가질 수 있습니다.

예를 들어, ∠ 270°(직선)로 각진 벡터는 -90°의 각도를 갖는다고 말할 수도 있습니다. (아래 그림) 위의 오른쪽 벡터(7.81 ∠ 230.19°)는 7.81 ∠ -129.81°로도 나타낼 수 있습니다.

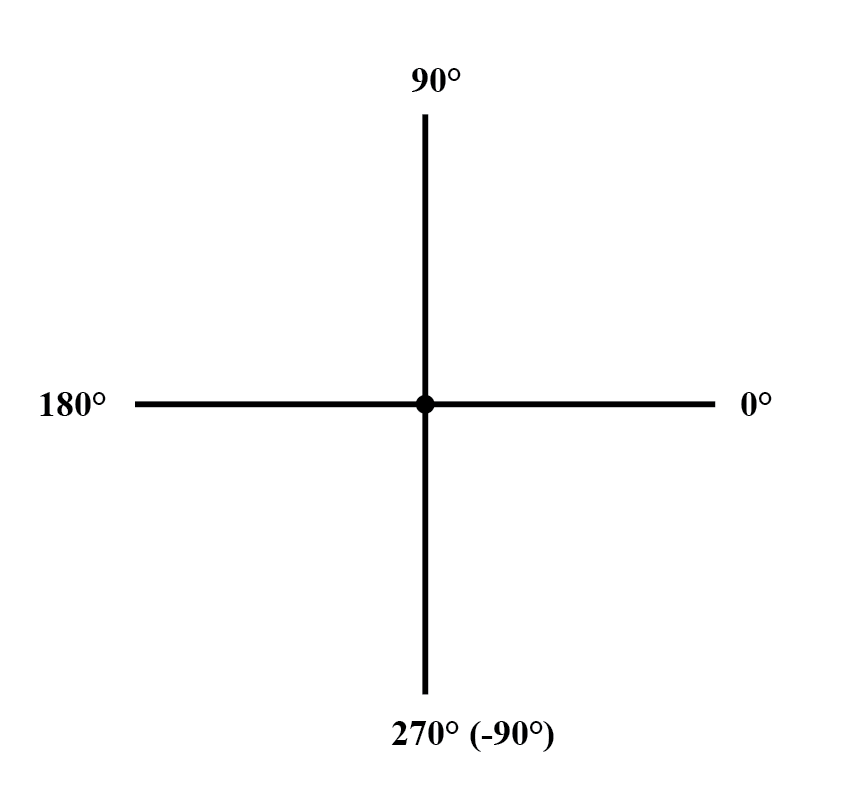
벡터 나침반.

복소수의 직사각형 형태

반면에 직사각형 형태는 복소수가 각각의 수평 및 수직 구성 요소로 표시되는 곳입니다. 본질적으로 각진 벡터는 직각 삼각형의 빗변으로 간주되며 인접한 변과 반대 변의 길이로 설명됩니다.

벡터의 길이와 방향을 크기와 각도로 나타내기보다 '좌/우 얼마나 멀리', '위/아래로 얼마나 멀리'로 기술한다.

이러한 2차원 도형(가로 및 세로)은 두 개의 숫자로 상징됩니다. 수평 및 수직 치수를 서로 구별하기 위해 수직에는 소문자 "i"(순수 수학) 또는 "j"(전자공학)가 접두사로 붙습니다.

이러한 소문자는 물리적 변수(예:소문자 "i"로 상징되는 순시 전류)를 나타내는 것이 아니라 수학적인 연산자입니다. 벡터의 수직 구성 요소와 수평 구성 요소를 구별하는 데 사용됩니다. 완전한 복소수로서 수평 및 수직 수량은 합계로 작성됩니다. (아래 그림)

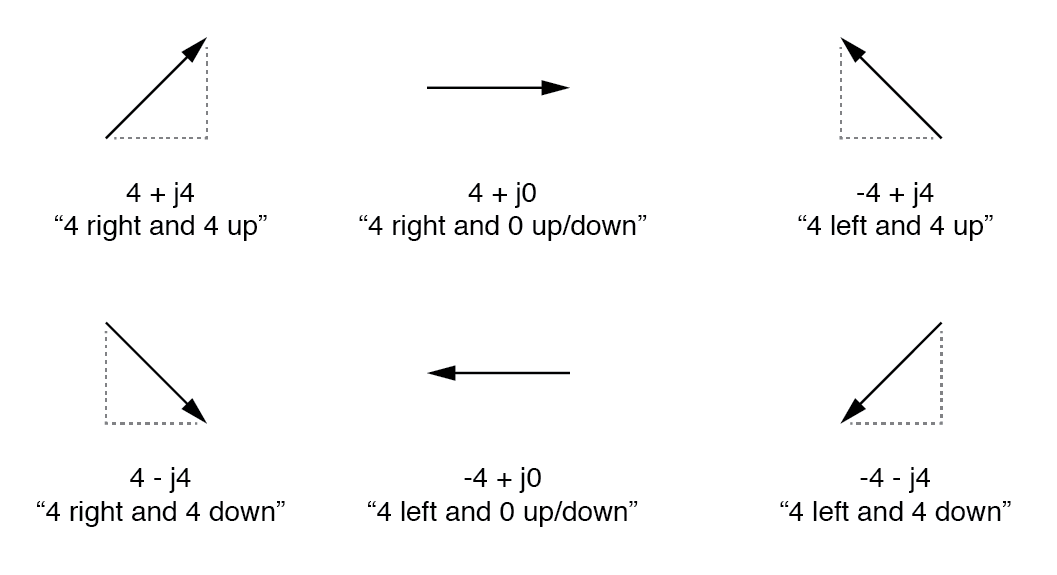
"직사각형" 형식에서 벡터의 길이와 방향은 수평 및 수직 범위로 표시되며, 첫 번째 숫자는 수평("실제")을 나타내고 두 번째 숫자는 수직("가상") 치수를 나타내는 숫자("j" 접두어 포함)

수평 구성요소는 실제 해당 차원이 일반 스칼라("실제") 숫자와 호환되기 때문에 구성요소입니다. 수직 구성요소는 가상이라고 합니다. 그 차원은 실수의 규모와는 완전히 다른 방향에 있기 때문입니다. (아래 그림)

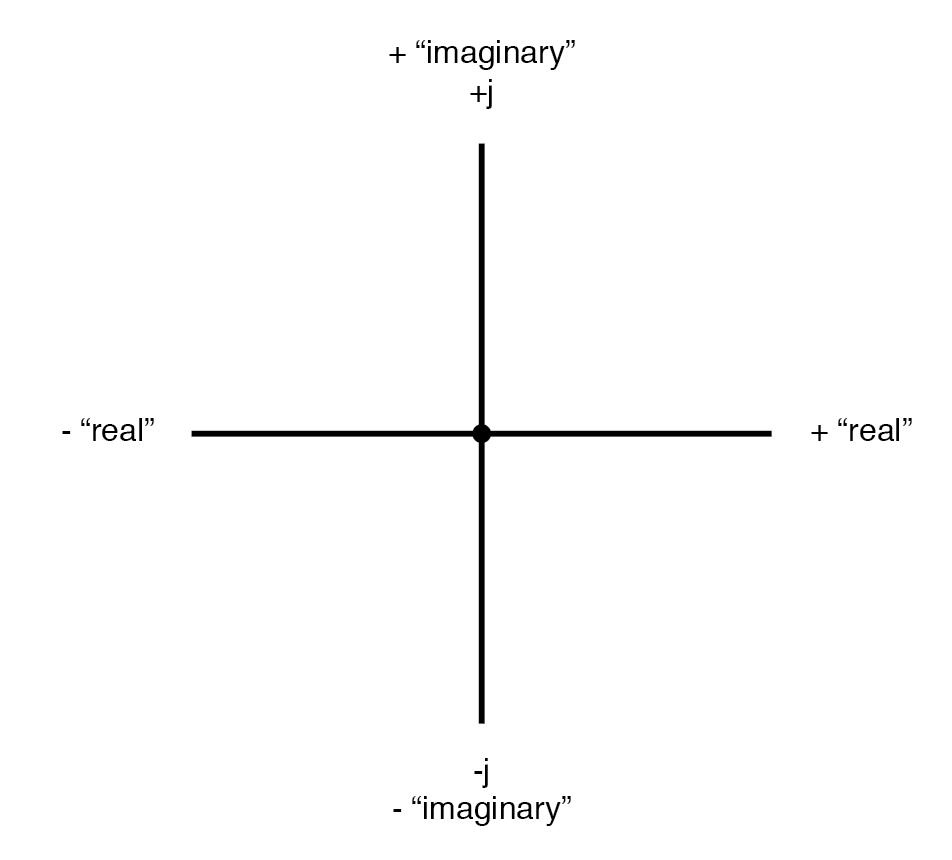
실수축과 허수축을 표시하는 벡터 나침반

그래프의 "실제" 축은 앞에서 본 친숙한 숫자 선에 해당합니다. 즉, 양수 값과 음수 값이 모두 있는 선입니다. 그래프의 "허수" 축은 "실제" 축에 대해 90°에 위치한 또 다른 숫자 선에 해당합니다.

벡터는 2차원이므로 이를 표현하기 위한 2차원 "지도"가 있어야 합니다. 따라서 서로 수직인 두 개의 숫자 선이 있어야 합니다. (아래 그림)

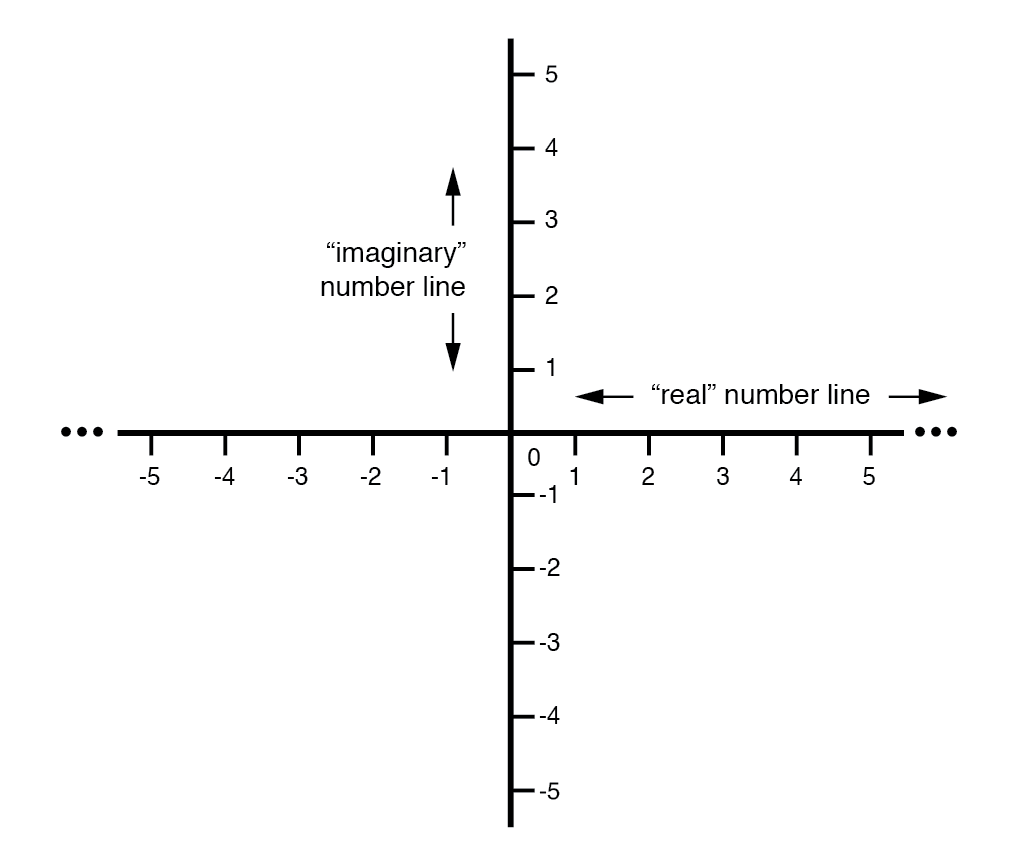
실수 및 허수("j") 숫자 선이 있는 벡터 나침반.

극형에서 직사각형으로 변환

두 표기법 모두 복소수에 유효합니다. 두 가지 표기법을 사용하는 주된 이유는 장형 계산의 용이함, 직사각형 형식은 덧셈과 뺄셈에 적합하고 극형은 곱셈과 나눗셈에 적합하기 때문입니다.

두 표기법 간의 변환에는 간단한 삼각법이 포함됩니다. 극에서 직사각형으로 변환하려면 극 크기에 각도의 코사인을 곱하여 실수 성분을 찾고 극 크기에 각도 사인을 곱하여 허수 성분을 찾습니다.

이것은 수량을 직각 삼각형의 변, 삼각형의 빗변은 벡터 자체(극좌표 형태를 구성하는 수평에 대한 길이와 각도), 수평 및 수직 변은 " 각각 실제" 및 "가상" 직사각형 구성요소:(아래 그림)

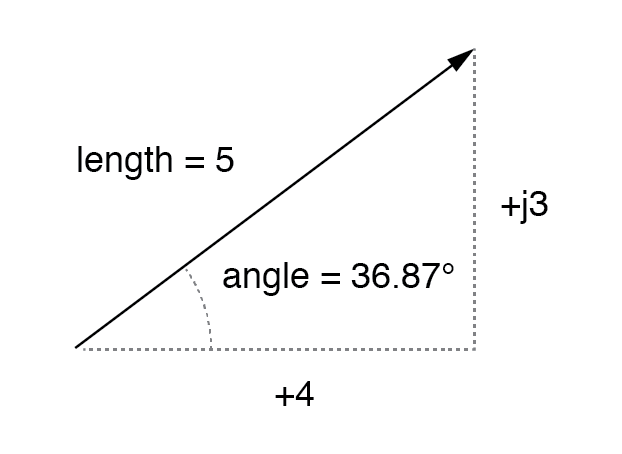
실수(4) 및 허수(j3) 구성 요소 측면에서 크기 벡터입니다.

직사각형에서 극형으로 변환

직사각형에서 극좌표로 변환하려면 피타고라스 정리(극성 크기는 직각 삼각형의 빗변, 실수 성분 및 허수 성분은 각각 인접 변과 반대 변)를 사용하여 극 크기를 구하고 다음과 같이 각도를 구합니다. 허수 성분의 아크탄젠트를 실수 성분으로 나눈 값:

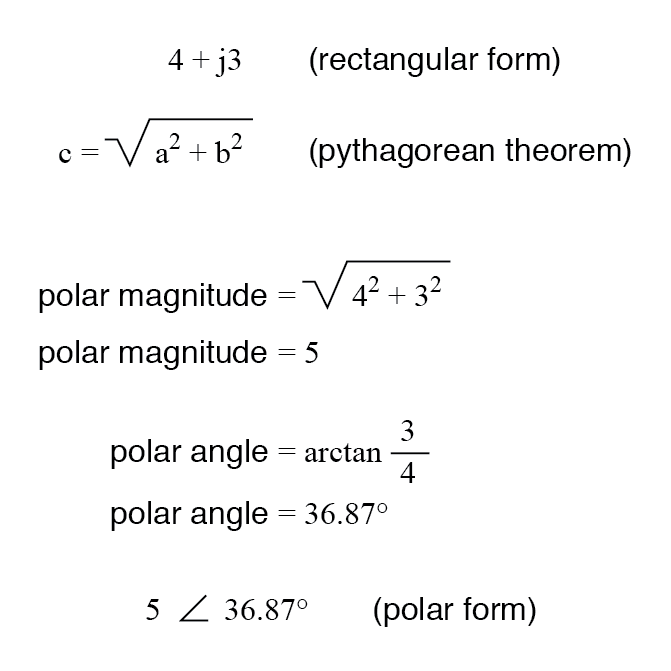
검토:

<울>

극극 표기법은 시작점에서 벡터의 길이와 각도 방향으로 복소수를 나타냅니다. 예:45마일 ∠ 203°(서에서 남서로)를 비행합니다.

직사각형 표기법은 수평 및 수직 차원의 복소수를 나타냅니다. 예:서쪽으로 41마일을 운전한 다음 방향을 돌려 남쪽으로 18마일을 운전하십시오.

직사각형 표기법에서 첫 번째 수량은 "실제" 구성요소(벡터의 수평 치수)이고 두 번째 수량은 "허수" 구성요소(벡터의 수직 치수)입니다. 허수 구성요소 앞에 소문자 "j"가 옵니다. 때로는 j 연산자라고도 합니다. .

복소수에 대한 극 및 직사각형 표기법은 모두 직각 삼각형의 형태로 그래픽적으로 관련될 수 있으며 빗변은 벡터 자체를 나타냅니다(극성 형식:빗변 길이 =크기, 수평 측면에 대한 각도 =각도 ), 직사각형 "실제" 구성요소를 나타내는 수평면, 직사각형 "허수" 구성요소를 나타내는 수직면.

관련 워크시트:

<울>

AC 단계 워크시트