나노물질








이 논문에서 우리는 전통적인 UV 리소그래피 방법과 DC 스퍼터링 증착에 의해 두께가 다른 일련의 FeCoBSi 다층 패턴 자성 필름을 제작했습니다. 고주파 특성 특성화 동안 넓은 공진 대역 현상이 관찰되었으며, 막 두께가 45nm일 때 FWHM(전폭 반치폭)이 4GHz입니다. 넓은 공명 대역 효과는 결합된 줄무늬 패턴의 줄무늬 폭이 다르기 때문에 다중 공명 피크가 존재하는 데 기여했으며, 이는 각 줄무늬에서 구별되는 모양 이방성 필드를 유도했습니다. 각 공진 피크는 스트라이프 사이의 간격으로 인해 독립적이어서 이러한 구조의 마이크로파 특성을 조정하는 제어 가능한 방법을 제공합니다. 두께가 다양하면 공명 밴드가 수학적 예측에 따라 변경될 수 있습니다. 이 연구는 자화 역학에서 마이크로파 공명 특성을 조정하는 효과적인 방법을 제시합니다.
<섹션 데이터-제목="배경">통신 기술의 급속한 발전과 함께 고주파에서 이러한 시스템의 성능을 저하시키는 EMI(Electromagnetic Inference) 문제가 크게 주목받고 있다[1,2,3,4,5]. EMI 차폐 재료의 요구 사항을 충족하기 위해 광대역 및 자성 필름의 제어 가능한 공진이 요구됩니다[6, 7]. 한편, 설계된 주파수에서 높은 감쇠 계수는 유망한 EMI 장치를 구현하는 데 기여할 것입니다[8, 9]. 필름의 면내 단축 이방성은 기가헤르츠 주파수에서 연자성 특성을 잘 이끌어 낼 수 있으며, 따라서 더 나은 흡수 특성, 유도 자기장[10], 증착 중 유도 응력[11], 다층 설계[12]를 포함한 여러 방법 , 및 외부 자기장 하에서의 포스트 어닐링[13, 14]이 조사되었습니다. 또한 인공 구조로 설계된 유도 형상 이방성을 갖는 패턴화된 자성 필름은 제어 가능하고 견고한 특성으로 인해 큰 관심을 끌고 있습니다[15, 16]. 이러한 관점에서 우리의 이전 연구에서 이중 줄무늬 패턴의 FeCo 기반 자성막이 제안되었다[17]. 이중 공명 피크 현상이 있는 넓은 공명 대역이 실험 중 관찰되었으며, 이는 독립적인 자기 줄무늬에 의해 기여한 이중 공진 소스의 중첩으로 인한 것입니다.
따라서 본 논문에서는 공진 대역을 더욱 확장하기 위해 5가지 다른 너비의 다양한 스트라이프를 포함하는 독특한 결합 스트라이프 패턴 FeCoBSi 박막을 도입하고 Landau-Lifshitz-Gilbert(Landau-Lifshitz-Gilbert LLG) 행렬 운동 형식론. 넓은 공진 대역 현상은 실험을 위해 얇은 두께, 즉 45nm에서 4GHz의 반치폭(FWHM)으로 향상되었습니다. 한편, 공진 주파수의 변화는 자기소거 인자와 관련된 수학식으로 예측할 수 있었다. 결과는 실제 응용에서 전통적인 리소그래피 공정으로 제어할 수 있게 하는 고유한 스트라이프 너비로 인한 형상 유도 유효 이방성으로 더 설명될 수 있습니다.
Fe66 공동17 B16 시1 실온에서 DC 마그네트론 스퍼터링에 의해 서로 다른 두께의 박막이 실리콘(111) 기판에 증착되었습니다. 그림 1과 같이 면내 단축 이방성을 유도하기 위해 기판의 단축을 따라 500Oe의 외부 자기장을 인가했습니다. 전통적인 자외선(UV) 리소그래피 기술과 리프트 오프 방법을 사용하여 결합된 스트라이프 패턴을 제작했습니다. 폭이 다른 다양한 스트라이프를 포함하는 결합된 스트라이프 패턴의 FeCoBSi 필름이 처리되었습니다. 줄무늬는 너비 순서가 각각 5, 10, 15, 20, 25μm로 연속적으로 배열되었습니다. 독특한 줄무늬의 분리 간격은 5μm로 고정되었습니다. 패턴화된 필름의 두께는 45~135nm로 다양했습니다.
<그림>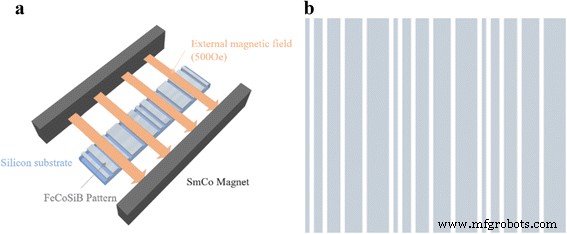
증착 중 외부 유도 자기장의 구조(a ) 및 결합된 줄무늬 패턴 자기 필름(b ). 각 줄무늬의 너비는 각각 5, 10, 15, 20, 25μm였습니다. 두 줄무늬 사이의 간격 너비는 5μm로 고정되었습니다. 필름의 최종 구조를 노출시키기 위해 증착 후 리프트 오프 공정을 수행했습니다.
필름의 두께는 주사전자현미경(SEM)으로 단면 관찰하여 결정하였다. 자성 필름의 해당 정적 특성, 즉 히스테리시스 루프는 진동 샘플 자력계(VSM)에 의해 측정되었습니다. 마이크로파 특성은 0.5~6GHz의 주파수 범위에서 벡터 네트 분석기에 연결된 단락된 마이크로 스트립 전송 라인 섭동 방법을 특징으로 합니다.
그림 1a는 외부 유도 자기장을 사용한 증착 설정 방식을 보여줍니다. 면내 단축 이방성을 유도하기 위해 증착 동안 500O의 외부 자기장이 적용되었습니다. 증착 후 리프트 오프 방법을 처리하여 패턴화된 필름 구조에 노출시켰다. 그림 1b는 자성 필름의 결합된 스트라이프 패턴 구조를 보여줍니다. 각 줄무늬의 너비 순서는 각각 5, 10, 15, 20, 25μm에 해당하며 각 줄무늬 사이의 간격은 5μm로 고정되었습니다. 우리의 이전 연구에 따르면 XRD 측정 동안 기판에서 Si(111)을 제외하고 명백한 결정성 피크가 없었습니다[18]. 따라서 우리 필름의 결정 구조는 비정질 또는 나노결정이었습니다.
45~135nm의 다양한 두께로 증착된 결합된 스트라이프 패턴 필름의 정적 자기 특성을 조사했습니다. 쉬운 축은 유도 자기장의 방향과 동일하고 하드 축은 이에 직교하는 방향으로 정의되었습니다(그림 2). M/Ms의 현재 부분 - 현장에서 측정한 필름의 H 루프는 100~- 100 범위 Oe . 쉬운 축과 단단한 축의 차이는 유도 자기장과 줄무늬 모양의 이방성에 의해 야기된 유도된 면내 단축 이방성을 명확하게 보여줍니다. 또한, 그림 2의 히스테리시스 루프는 H ch 최저 13 O, 여기서 H ch 하드 축을 따른 보자력 및 H ce 쉬운 축을 따른 보자력입니다. 필름 두께가 증가함에 따라 H ch Herzer가 제안한 무작위 이방성 모델에 따라 45nm에서 32Oe에서 135nm에서 13Oe로 감소했습니다[19]. 모든 세부 사항은 이전 작업 [18]에서 찾을 수 있습니다.
<사진>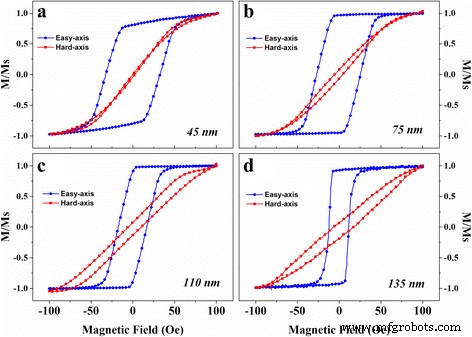
두께가 다른 결합된 스트라이프 패턴 자성 필름의 히스테리시스 루프. 결과는 각 그림에서 유도 자기장 방향으로 정의된 easy-hard 축에서 나타납니다. a에서 d까지 , 필름의 두께는 45nm에서 135nm까지 다양했습니다.
그림 3은 다양한 두께의 주파수 함수에 대한 결합된 스트라이프 패턴 필름의 투과 스펙트럼의 실수 및 허수 성분을 보여줍니다. <>t =45nm, f에 나타나는 분할 공명 피크가 있습니다. 낮음 그리고 f 높음 측정된 주파수 범위에 대한 주파수. 이 그래프에 따르면 t =45 nm, μ'는 약 170에서 높고 f 낮음 약 3.2GHz에 도달하고 f 높음 약 5GHz입니다. 두께가 증가함에 따라 <>f 값 낮음 항상 증가합니다. t 동안 =135nm, μ' 여전히 적절한 수준인 170을 유지할 수 있습니다. f 낮음 f 높음 측정된 주파수 범위 6GHz를 벗어났을 수 있습니다. 반치폭(FWHM)으로 정의되는 공진 대역은 2GHz의 이중 줄무늬 패턴 필름의 FWHM보다 넓은 45nm 두께에서 4GHz 이상으로 확장되었습니다[18]. 광대역 마이크로파 EMI 흡수체로서 미래의 응용을 위한 더 나은 길을 열 수 있습니다. 밴드 확장 현상은 5개의 다른 너비 스트라이프에 의해 유도된 다른 모양 이방성 필드 때문입니다. 간격의 고정 너비를 5μm로 생각하면 결합 효과 없이 두 개의 연속 스트라이프를 자기적으로 분리할 수 있을 만큼 충분히 큽니다. 따라서 각 스트라이프는 실제로 서로 독립적이어서 마이크로파 여기에서 별도의 자기 응답을 초래합니다. 고주파 전자기장에 대한 총 응답은 5개의 다른 너비 스트라이프를 수학적으로 더한 것이어야 합니다. 또한, 형상 이방성은 필름의 유효 이방성, 즉 공진 주파수를 결정하는 데 필수적인 역할을 할 수 있습니다[20]. 따라서, 미소자석 해석 시의 자기소거 인자를 고려할 필요가 있다. 박막의 동적 특성을 입증하기 위해 LLG Gilbert 방정식 [21]과 자기소거 효과를 사용하여 단축 이방성을 갖는 자기 박막의 고주파 현상을 설명했습니다. 따라서 고주파 투과성은 다음 방정식으로 설명될 수 있습니다.
<그림>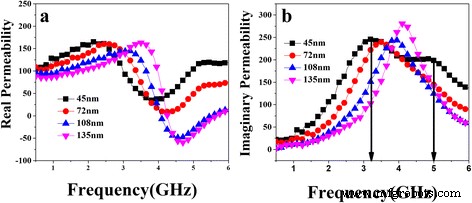
다양한 두께의 결합된 스트라이프 패턴의 FeCoBSi 박막의 실온에서 측정된 투과성 스펙트럼은 필름의 실제 투과성을 나타냅니다(a ) 및 가상 투자율(b )
$$ \mu =1+\frac{2}{3}\frac{\gamma 4\pi {M}_s\left\{\gamma \left[{H}_e+4\pi {M}_s\left ({N}_x-{N}_z\right)\right]+ i\omega \alpha \right\}}{\left\{\gamma \left[{H}_e+4\pi {M}_s\ 왼쪽({N}_x-{N}_z\right)\right]+ i\omega \alpha \right\}\left\{\gamma \left[{H}_e+4\pi {M}_s\left ({N}_y-{N}_z\right)\right]+ i\omega\alpha\right\}-{\omega}^2} $$ (1)여기서 4πM s 포화 자화로 정의됩니다. α 감쇠 계수, γ 는 자이로 자기비(1.76 × 10 7 ) 오에 −1 s −1 FeCo 합금용), H e 유효 등방성이 제출되고, N x , N 와 , N z 는 각각 3개의 직교 방향에 따른 자기소거 인자입니다. f r 다음과 같이 Kittle 방정식에 의해 유도될 수 있습니다.
$$ fr=\frac{\gamma }{2\pi }{\left\{\frac{\left[{H}_e+4\pi {M}_s\left({N}_y-{N}_z \right)\right]\left[{H}_e+4\pi {M}_s\left({N}_x-{N}_z\right)\right]}{1+2{a}^2} \right\}}^{1/2} $$ (2)우리 필름에 포함된 다양한 너비의 줄무늬에 비추어 볼 때 독특한 모양 이방성을 유발하여 분할 공명 피크를 유발하므로 전체 스펙트럼은 5개의 개별 1을 수학적 추가로 특성화해야 합니다. x에 따른 자기소거 계수 , y , 및 z 방향은 [20]
으로 쓸 수 있습니다. $$ {N}_y=\frac{2}{\pi }{\tan}^{-1}\frac{T\sqrt{W^2+{T}^2+{L}^2}}{ WL} $$ (3) $$ {N}_x=\frac{2}{\pi }{\tan}^{-1}\frac{W\sqrt{W^2+{T}^2+{ L}^2}}{TL} $$ (4) $$ {N}_z=1-{N}_x-{N}_y $$ (5)여기서 L 는 z에 따른 길이입니다. -축, W x의 너비입니다. -축 및 T y에 따른 두께입니다. -중심선. 공식 (3), (4), (5) 및 LLG 공식을 사용하여 5~25μm의 서로 다른 마그네틱 띠 폭에 해당하는 공진 주파수를 각각 계산할 수 있습니다.
그림 4는 두께가 5~25μm인 별개의 줄무늬에 대해 계산된 공진 주파수를 보여줍니다. 이 계산에서 α 공진 주파수의 위치에 약간의 영향을 미치는 0.03으로 설정하였다. 연속 FeCoBSi 필름의 실험 결과에서 추출한 포화 자화 및 유효 평면 내 이방성 필드는 1345 emu/cm 3 로 설정되었습니다. 및 40 Oe [18], 각각. 비정질 자성막에서 자기결정 이방성은 무시될 수 있으며, 이는 [20]에서 입증된 공진 주파수 결정 과정에서 형상 이방성이 갖는 보다 본질적인 역할로 이어진다. 따라서 서로 다른 너비의 스트라이프는 갭에 의해 유지되는 분리 효과로 인해 독특한 공명 피크에 기여해야 하며 이론적으로 스펙트럼에서 다중 공명 피크를 생성합니다. 또한, 막 두께가 증가함에 따라 주 공진 주파수가 증가하고 너비가 다른 줄무늬 사이의 주파수 차이(그림 4 참조)가 향상되었습니다. 따라서 필름의 두께가 충분히 얇으면 다중 공진 피크 사이에 강력한 수퍼 포지셔닝 효과가 있으며 이 경우 자기 스펙트럼 대역이 확연하게 넓어진 거동을 나타냅니다. 두께가 증가함에 따라 공진 주파수 차이가 더 뚜렷하기 때문에 이러한 중첩 효과가 약해졌습니다. 두께가 110nm 이상으로 증가함에 따라 5μm와 같은 특정 너비의 줄무늬의 공진 주파수는 파란색 영역이 표시되어 측정 범위를 벗어났고 결과적으로 45nm 필름에 비해 FWHM이 더 작아졌습니다. 공진 주파수는 수학적 계산과 관련하여도 예측할 수 있습니다. 필름의 두께뿐만 아니라 줄무늬의 너비를 조정하여 각 공진 현상을 제어하여 실제 적용할 수 있습니다.
<그림>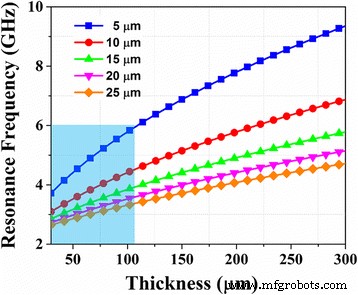
다른 두께에 따라 다른 스트라이프 너비의 공진 주파수의 수치 계산. 파란색 영역은 설정에 사용할 수 있는 측정 주파수 범위(최대 6GHz)를 나타냅니다.
밴드 확장 효과가 별도의 스트라이프에 의해 유도된 독립적인 공진 피크의 중첩에 기인한다는 가정은 그림 5의 피팅 결과에서 명확하게 이해할 수 있습니다. 우리의 가정을 검증하기 위해 단일 스트라이프 패턴 필름의 자기 스펙트럼은 다음과 같습니다. 도 계산됨. 결합된 스트라이프 패턴 필름과 비교하여 각 스트라이프의 공진 주파수는 빨간색 영역과 같이 결합된 스트라이프 패턴의 FWHM 범위에서 떨어졌으며 이는 결합 스트라이프 패턴 필름의 밴드 확장 현상이 중첩에 의한 것이라는 우리의 가정을 잘 뒷받침합니다. 서로 다른 줄무늬에 의해 유도된 독특한 공명 피크.
<그림>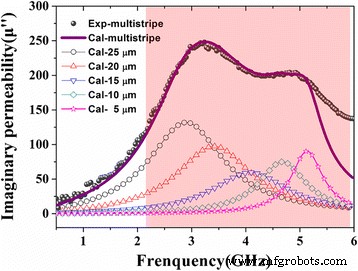
T가 있는 결합된 스트라이프 패턴의 FeCoBSi 박막에 대한 측정 및 계산된 가상 투자율 =45nm이고 너비가 다른 줄무늬에 대해 계산된 가상 투자율입니다. 빨간색 영역은 결합된 스트라이프 패턴 필름의 공명 대역(FWHM)에 해당합니다.
결론적으로, 우리는 두께가 다른 결합된 스트라이프 패턴의 FeCoBSi의 자기 및 마이크로파 공명 특성을 연구했습니다. 이전의 이중 줄무늬 패턴 필름과 비교하여 5줄 패턴의 FeCoBSi 패턴은 공명 대역(FWHM)을 4GHz까지 더 확장할 수 있습니다. 확장 밴드 현상은 실제 응용 분야의 요구 사항을 충족시키기 위해 자성 필름의 두께뿐만 아니라 다른 스트라이프의 너비를 조정하여 제어할 수 있으며 이는 향후 EMI 장치에 유용할 수 있습니다.
전자기 추론
전체 너비 절반 최대
Landau-Lifshitz-Gilbert
나노물질
초록 폴리아닐린 나노섬유를 가지는 폴리아닐린 나노스킨(PANS)이 개발되었습니다. PANS는 순차적인 추출, 가열 및 팽창 과정을 통해 공식화되었습니다. X선 광전자 분광법, 푸리에 변환 적외선 분광법, 열중량 분석법, 브루나우어-에메트-텔러 분석법을 이용하여 PANS의 조성을 분석한 결과, PANS가 유기 물질로만 구성되어 있음을 알 수 있습니다. 또한 PANS는 주변 산성 환경에 따라 전환 가능한 흡광도 특성을 보여주고 있으며 이러한 특성을 이용하여 주변 산화환원 상태 변화를 감지할 수 있는 가능성을 제시하고 있다. 소개
초록 Poly(vinylidene fluoride, PVDF)의 전기 활성 β-phase는 가장 높은 pyro- 및 piezoelectric 특성으로 인해 가장 바람직한 형태로 유연한 센서, 웨어러블 전자 장치 및 에너지 수확기 등으로 사용할 수 있습니다. 이 연구에서 , 우리는 기계적 스트레칭 및 전기 방사에 의해 고함량 β상 PVDF 필름 및 나노섬유 메쉬를 얻는 방법을 성공적으로 개발했습니다. 연신된 필름 및 나노섬유 메쉬의 상전이 과정과 초전 및 압전 효과는 편광 현미경(PLM) 이미지를 모니터링하여 각각 전류 및 개방 전