SPICE는 아날로그 전자 회로를 시뮬레이션하도록 설계된 컴퓨터 프로그램입니다. 원래 의도는 집적 회로의 개발을 위한 것이었으며 그 이름에서 S라는 이름이 파생되었습니다. 시뮬레이션 P 나와의 프로그램 통합된 C ircuit E 강조합니다. SPICE의 기원은 CANCER라는 다른 회로 시뮬레이션 프로그램으로 거슬러 올라갑니다. UC의 Ronald Rohrer 교수가 개발했습니다. Berkeley는 1960년대 후반에 그의 몇몇 제자들과 함께 1970년대 초반까지 계속해서 개선되었습니다. Rohrer가 버클리를 떠날 때 CANCE

“Electronics Workbench를 사용하면 종이에 이미 익숙한 것과 똑같이 보이는 회로도를 생성할 수 있으며 전원 스위치를 뒤집어 회로도가 실제 회로처럼 작동하도록 할 수 있습니다. 다른 전자 시뮬레이터를 사용하면 SPICE 노드 목록을 텍스트 파일로 입력해야 할 수도 있습니다. 이는 고급 전자 엔지니어를 제외한 모든 능력을 넘어서는 회로의 추상적 표현입니다. —(Electronics Workbench 사용자 가이드—버전 4, 7페이지) 이 소개는 Electronics Workbench라는 회로 시뮬레이션 프로그램의 작

해가 숫자인 일반 방정식과 달리 미분 방정식은 해가 실제로 함수이고 미지 함수의 최소 하나의 도함수가 방정식의 일부인 미분 방정식입니다. 함수의 역도함수를 찾을 때와 마찬가지로 하나 이상의 가능성을 포함하는 솔루션이 종종 남습니다(반도함수에서 일반적으로 발견되는 상수 c의 가능한 많은 값을 고려). 모든 미분 방정식에 답하는 함수 집합을 해당 미분 방정식의 일반 솔루션이라고 합니다. 해당 집합의 함수 중 하나는 해당 미분 방정식에 대한 특정 솔루션이라고 합니다. 미분방정식 내에서 미분과 적분을 위한 기준변수를 독립변수라고 합니다.

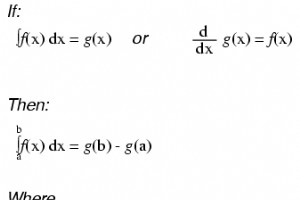
관련 워크시트: 전기 회로 미적분 워크시트

일정 규칙 합계의 법칙 차이의 법칙

참고:이것은 e의 매우 독특하고 유용한 속성입니다. 도함수의 경우와 마찬가지로 이러한 함수의 역도함수는 동일한 함수입니다. 역도함수의 경우에도 끝에 상수 c가 추가됩니다.

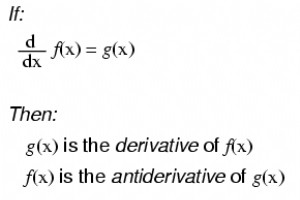
여기서 중요한 사실에 주목하십시오. f(x)의 도함수를 취하면 정확히 g(x)를 얻을 수 있지만 g(x)의 역도함수를 취하면 반드시 원래 형식의 f(x)를 얻을 수 없습니다. 예: 상수 c를 알 수 없다는 점에 유의하십시오! 원래 함수 f(x)는 3x2일 수 있습니다. + 5, 3x2 + 10, 3x2 + 무엇이든 , 그리고 f(x)의 도함수는 여전히 6x였을 것입니다. 함수의 역도함수를 결정하는 것은 함수의 도함수를 결정하는 것보다 약간 덜 확실합니다. 관련 워크시트: 전기 회로 미적분 워크시트

상수 규칙 합계의 법칙 차이의 법칙 제품 규칙 몫 규칙 권력 규칙 다른 기능의 기능 관련 워크시트: 전기 회로 미적분 워크시트

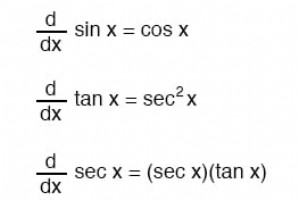
관련 워크시트: 전기 회로 미적분 워크시트

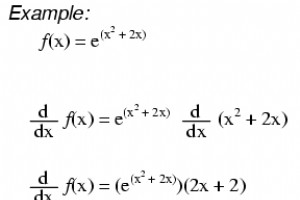
e의 도함수의 예 비례 상수 우리가 관계나 현상이 기하급수적이라고 말할 때, 우리는 전류, 이윤, 인구와 같은 일부 양은 양이 증가함에 따라 더 빠르게 증가한다는 것을 의미합니다. 즉, 주어진 변수에 대한 변화율은 그 변수의 값에 비례합니다. 이는 지수 함수의 도함수가 원래 지수 함수에 상수(k ) 비례를 설정합니다. $$\frac{\text{d}}{\text{d}x}a^x=ka^x$$ 비례 상수는 지수 밑의 자연 로그와 같습니다. $$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$

관련 워크시트: 전기 회로 미적분 워크시트

(c는 상수임) 관련 워크시트: 전기 회로용 미적분 워크시트

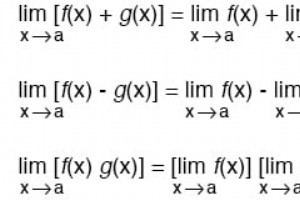
관련 워크시트: 전기 회로용 미적분 워크시트

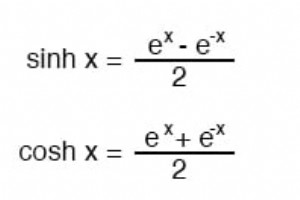
참고:모든 각도(x)는 라디안 단위로 표현되어야 합니다. 이러한 쌍곡선 함수에 대해. 원에는 2π 라디안이 있습니다(360o ).

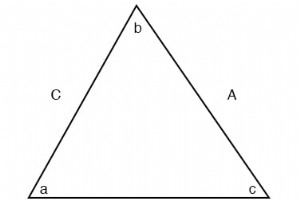
사인 법칙(모든 삼각형에 대해) 코사인 법칙(모든 삼각형에 대해)

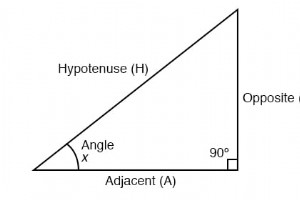
직각 삼각형 한 각도가 정확히 90o인 것으로 정의됩니다. (직각 ). 삼각 ID H는 빗변입니다. , 항상 직각 반대입니다. 각도 x를 기준으로 O는 반대입니다. A는 인접한 . arcsin, arccos 및 arctan과 같은 Arc 함수는 일반 삼각 함수의 보완입니다. 이 함수는 비율 입력에 대한 각도를 반환합니다. 예를 들어 탄젠트가 45o인 경우 1과 같으면 1의 arctangent(arctan)는 45o입니다. . 호 기능은 한 변의 길이를 알고 있는 경우 직각 삼각형의 각도를 찾는 데 유용합니

연립 방정식 및 연립 방정식이란 무엇입니까? 동시 방정식이라는 용어 및 방정식 시스템 2개 이상의 미지의 변수가 동일한 수의 방정식을 통해 관련되어 있는 조건을 말합니다. 예: 이 방정식 세트의 경우 x 값의 단일 조합만 있습니다. 그리고 y 두 가지 모두를 만족시킬 것입니다. 개별적으로 고려되는 두 방정식은 유효한 (x,y)의 무한대를 가집니다. 솔루션이지만 함께 하나만 있습니다. 그래프에 표시하면 이 조건이 명확해집니다. 각 선은 실제로 가능한 x를 나타내는 점의 연속체입니다. 그리고 y 각 방정식에

팩토리얼의 정의 “!” 기호로 표시 정수 뒤; 해당 정수와 1로 내려가는 모든 정수의 곱.팩토리얼의 예: 5! =5 x 4 x 3 x 2 x 1 5! =120 이상한 계승 0! =1 1! =1 관련 워크시트: Phasor 수학 워크시트