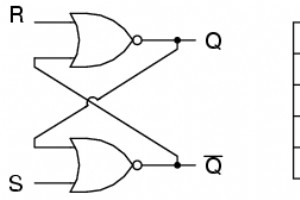
쌍안정 멀티바이브레이터는 2 접두사 bi로 표시되는 안정 상태 그 이름으로. 일반적으로 하나의 상태를 set이라고 합니다. 다른 하나는 재설정으로 . 따라서 가장 단순한 쌍안정 장치를 set-reset이라고 합니다. , 또는 S-R, 래치. S-R 래치를 생성하기 위해 다음과 같이 하나의 출력이 다른 입력으로 피드백되고 그 반대의 경우도 마찬가지 방식으로 두 개의 NOR 게이트를 연결할 수 있습니다. Q 및 not-Q 출력은 반대 상태에 있어야 합니다. S와 R 입력을 모두 1과 같게 하면 Q와 not-Q가 모두 0이

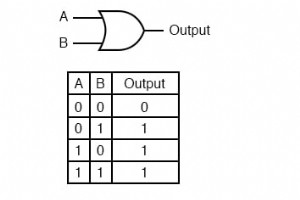
간단한 게이트 및 조합 논리 회로를 사용하면 주어진 입력 상태에 대해 명확한 출력 상태가 있습니다. OR 게이트의 진리표를 예로 들어 보겠습니다. 네 가지 가능한 입력 상태 조합(0-0, 0-1, 1-0 및 1-1) 각각에 대해 하나의 명확하고 모호하지 않은 출력 상태가 있습니다. 다수의 계단식 게이트를 처리하든 단일 게이트를 처리하든 해당 출력 상태는 회로의 게이트에 대한 진리표에 의해 결정되며 다른 것은 없습니다. 그러나 이 게이트 회로를 변경하여 출력에서 ​​입력 중 하나로 신호 피드백을 제공하면 이상한 일이 발

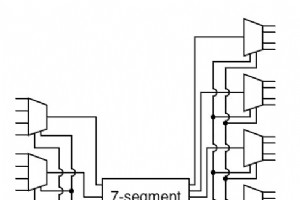
여러 회로를 함께 사용하는 예로서 4자리 7세그먼트 디스플레이에 4자리 숫자를 나타내는 16개의 입력을 가지지만 2진에서 7세그먼트 인코더는 하나만 사용하는 장치를 만들 것입니다. . 첫째, 회로의 전체 아키텍처는 제공된 설명과 같은 모양을 제공합니다. 이 회로를 따라가면 위에 제공된 설명과 일치하는지 확인할 수 있습니다. 16개의 기본 입력과 표시할 숫자를 선택하는 데 사용되는 2개의 추가 입력이 있습니다. 4자리 7세그먼트 디스플레이를 제어하기 위한 28개의 출력이 있습니다. 한 번에 4개의 기본 입력만 인코딩됩

멀티플렉서는 mux로 약칭되며 여러 입력과 하나의 출력이 있는 장치입니다. 멀티플렉서의 도식 기호는 2:1 멀티플렉서의 진리표는 다음과 같습니다. 나1 나0 AD00000010010001111001101011011111 회로의 일부로 1:2 디코더를 사용하면 이 회로를 쉽게 표현할 수 있습니다. 멀티플렉서는 디멀티플렉서와 ​​동일한 명명 규칙으로 확장할 수도 있습니다. 4:1 멀티플렉서 회로는 다음과 같습니다. 이것이 멀티플렉서의 공식적인 정의입니다. 비공식적으로는 혼선이 많다

디멀티플렉서는 때때로 dmux로 약칭되며 하나의 입력과 하나 이상의 출력이 있는 회로입니다. 회로가 많은 장치 중 하나에 신호를 보내려고 할 때 사용됩니다. 이 설명은 디코더에 대한 설명과 유사하게 들리지만 디코더는 많은 장치 중에서 선택하는 데 사용되는 반면 디멀티플렉서는 여러 장치 간에 신호를 보내는 데 사용됩니다. 디멀티플렉서는 자체 회로도 기호가 있을 정도로 자주 사용됩니다(아래 그림) 1:2 디멀티플렉서의 진리표는 다음과 같습니다. IAD0 D1 0000010010101101 회로의 일부로 1:2

인코더란 무엇입니까? 인코더는 일련의 신호를 코드로 변경하는 회로입니다. 1:2 디코더 진리표를 반대로 하여 2:1 라인 인코더 진리표를 만들어 봅시다. D1 D0 A010101 이 진리표는 약간 짧습니다. 완전한 진리표는 다음과 같습니다. D1 D0 A00 01010111 우리가 대답해야 하는 한 가지 질문은 이러한 다른 입력으로 무엇을 해야 합니까? 우리는 그들을 무시합니까? 추가 오류 출력을 생성하도록 합니까? 많은 회로에서 이 문제는 어떤 입력이 활성 상태인지 뿐만 아니라 입력이 활성화된 순서도 알기 위해

디코더는 코드를 신호 세트로 변경하는 회로입니다. 인코딩의 역순으로 수행하기 때문에 디코더라고 부르지만 인코더와 디코더는 설계하기 쉽기 때문에 디코더를 사용하여 연구를 시작하겠습니다. 디코더 유형 라인 디코더 일반적인 유형의 디코더는 n자리 이진수를 가져와서 2n으로 디코딩하는 라인 디코더입니다. 데이터 라인. 가장 간단한 것은 1-to-2 라인 디코더입니다. 진리표는 다음과 같습니다. 광고1 D0 001110 A는 주소이고 D는 데이터 라인입니다. D0 A 및 D1가 아닙니다. A입니다. 회로는 아래 그림과 같습니다.

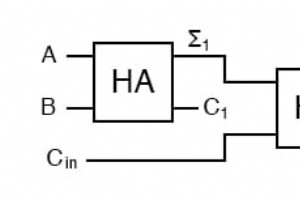
반가산기는 두 개 이상의 이진수 양을 더할 때까지 매우 유용합니다. 2진수 가산기를 개발하는 느린 방법은 진리표를 만들고 줄이는 것입니다. 그런 다음 세 개의 이진수 가산기를 만들기로 결정하면 다시 수행하십시오. 그런 다음 4자리 덧셈기를 만들기로 결정하면 다시 하십시오. 그러면 언제... 회로는 빠르지만 개발 시간은 느릴 것입니다. 두 개의 이진수 합계를 보면 여러 이진수로 더하기를 확장하는 데 필요한 것이 무엇인지 알 수 있습니다. 11 11 11 --- 110 중간 열이 사용하는 입력의 수를 보십시오. 가산기는 3개의

유용한 조합 논리의 첫 번째 예로서 두 개의 이진수를 더할 수 있는 장치를 만들어 보겠습니다. 답이 무엇인지 신속하게 계산할 수 있습니다. 0 + 0 =0 0 + 1 =1 1 + 0 =1 1 + 1 =102 따라서 두 개의 입력(및 b)과 두 개의 출력이 필요합니다. 저차 출력은 합을 나타내기 때문에 Σ라고 하고 고차 출력은 Cout라고 합니다. 수행을 나타내기 때문입니다. 진리표는 다음과 같습니다. ABΣC아웃 0000011010101101 부울 방정식을 단순화하거나 Karnaugh 맵을 만들면 아래와 같은 회로가

조합이라는 용어는 수학에서 왔습니다. 수학에서 조합은 순서가 지정되지 않은 집합입니다. 이는 항목이 어떤 순서로 들어왔는지 아무도 신경 쓰지 않는다는 공식 방식입니다. 대부분의 게임은 이런 식으로 작동합니다. 한 번에 하나씩 주사위를 굴려서 2 다음에 3이 나온다면 3 다음에 2를 낸 것과 같습니다. 조합 논리를 사용하면 입력이 변경되는 순서에 관계없이 회로가 동일한 출력을 생성합니다. 입력이 변경될 때 의존하는 회로가 있으며 이러한 회로를 순차 논리라고 합니다. 챕터 제목에서 순차 논리라는 용어를 찾을 수는 없지만 다음 몇 장에

더 큰 Karnaugh 맵은 더 큰 논리 설계를 줄입니다. 얼마나 큰 것이 충분히 큰가? 입력 수, 팬인에 따라 다릅니다. , 고려중인 논리 회로에. 대형 프로그래머블 로직 회사 중 하나에 답이 있습니다. 알테라의 고객 디자인 라이브러리에서 추출한 자체 데이터는 이질성의 가치를 뒷받침합니다. 로직 콘을 조사하고 LUT 기반 노드에 매핑하고 각 노드에서 가장 좋은 입력 수에 따라 정렬함으로써 Altera는 팬 인 분포가 2개에서 6개 입력 사이에서 거의 평평하다는 것을 발견했습니다. 5시에. 대답은 대부분의 모든 설계에 대해 6개

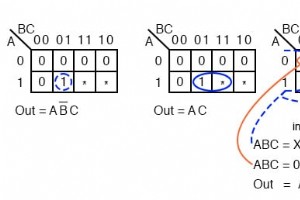
지금까지 입력 조건이 완전히 지정된 논리 축소 문제를 고려했습니다. 즉, 3변수 진리표 또는 Karnaugh 지도는 2n =23 또는 8개 항목, 전체 테이블 또는 지도. 일부 실제 문제에 대해 완전한 진리표를 항상 채울 필요는 없습니다. 전체 표를 채우지 않을 수도 있습니다. 예를 들어, 4비트로 인코딩된 BCD(Binary Coded Decimal) 숫자를 처리할 때 BCD 범위(0, 1, 2…9)를 초과하는 코드는 신경 쓰지 않을 수 있습니다. 16진수의 4비트 바이너리 코드(Ah, Bh, Ch, Eh, Fh)는 유효한 B

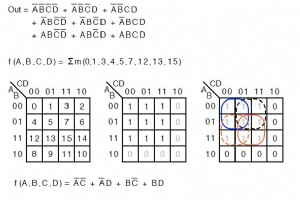
참고로 이 섹션에서는 Karnaugh 맵에 할당된 최소 항과 최대 항을 설명하기 위해 일부 텍스트에서 사용되는 용어를 소개합니다. 그렇지 않으면 여기에 새로운 자료가 없습니다. Minterms 용어 Σ(시그마)는 합을 나타내고 소문자 m은 최소항을 나타냅니다. Σm은 최소항의 합을 나타냅니다. 우리의 요점을 설명하기 위해 다음 예를 다시 살펴보겠습니다. 단순화되지 않은 논리에 대한 부울 방정식 설명 ​​대신 최소항을 나열합니다. f(A,B,C,D) =Σm(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15)

지금까지 우리는 논리 감소 문제에 대한 SOP(Sum-Of-Product) 솔루션을 찾았습니다. 이러한 각 SOP 솔루션에는 애플리케이션에 따라 더 유용할 수 있는 POS(생산적합) 솔루션도 있습니다. 합산 솔루션을 작업하기 전에 몇 가지 새로운 용어를 도입해야 합니다. 제품 용어 매핑에 대한 아래 절차는 이 장의 새로운 내용이 아닙니다. 우리는 maxterms에 대한 새로운 절차와 비교하기 위해 minterms에 대한 공식적인 절차를 수립하고자 합니다. 단기 미팅 1이 되는 부울 표현식입니다. 단일 셀 출력의 경

그레이 코드를 생성하는 방법을 알면 더 큰 지도를 만들 수 있습니다. 사실, 우리가 해야 할 일은 3-변수 맵의 상단을 가로질러 왼쪽에서 오른쪽 순서로 살펴보고 4-변수 맵의 왼쪽 아래로 복사하는 것입니다. 아래를 참조하십시오. 4개의 변수 K 맵 축소 다음 4개의 변수 Karnaugh 맵은 부울 대수에 대해 너무 지루한 부울 표현식의 감소를 보여줍니다. 부울 대수를 사용하여 줄일 수 있습니다. 그러나 Karnaugh 지도는 특히 수행할 논리 축소가 많은 경우 더 빠르고 쉽습니다. 위의 부울 표현식에는 7

지금까지 수행한 논리 단순화 예제는 부울 대수를 사용하여 거의 빠르게 수행할 수 있었습니다. 현실 세계의 논리 단순화 문제는 더 큰 Karnaugh 지도를 요구하므로 진지한 작업을 수행할 수 있습니다. 우리는 이 섹션에서 몇 가지 인위적인 예제를 작업하고 조합 논리 장에 대한 실제 응용 프로그램의 대부분을 남겨 둡니다. 인위적으로 기술을 설명하는 예를 의미합니다. 이 접근 방식은 조합 논리 장에서 보다 복잡한 응용 프로그램으로 전환하는 데 필요한 도구를 개발할 것입니다. Karnaugh 지도 및 그레이 코드 시퀀스 이전에 개발

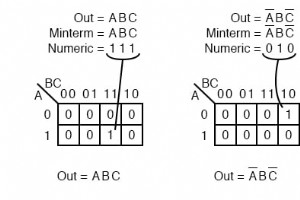
Karnaugh 지도는 누가 개발했습니까? 통신 엔지니어인 Maurice Karnaugh는 1953년 Bell Labs에서 Karnaugh 지도를 개발하면서 디지털 논리 기반 전화 교환 회로를 설계했습니다. Karnaugh 지도의 사용 이제 벤 다이어그램을 사용하여 Karnaugh 맵을 개발했으므로 사용하도록 하겠습니다. Karnaugh 지도 감소 논리 함수는 부울 대수에 비해 더 빠르고 쉽게 기능합니다. 감소란 단순화하여 게이트 및 입력 수를 줄이는 것을 의미합니다. 우리는 논리를 최저 비용 으로 단순화하고자 합니다. 구성

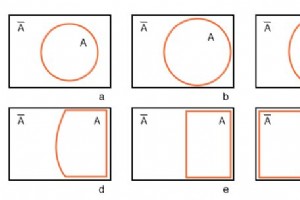
A 원으로 시작 직사각형 A 우주에서 아래 그림(a)에서 우리는 벤 다이어그램을 거의 Karnaugh 지도로 모핑합니다. 서클 A를 확장합니다. (b) 및 (c)에서 직사각형 A 우주를 따릅니다. (d)에서 A를 변경합니다. (e)에서 직사각형으로. A 외부에 남은 모든 것 A . A 에 직사각형을 할당합니다. (f)에서. 또한 Karnaugh 맵에서는 음영을 사용하지 않습니다. 우리가 지금까지 가지고 있는 것은 1-변수 Karnaugh 맵과 유사하지만 거의 유용하지 않습니다. 여러 변수가 필요합니다. 위

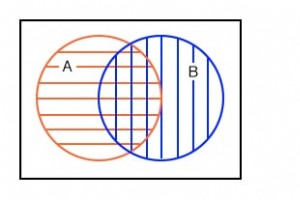
네 번째 예에는 A가 있습니다. 부분적으로 겹치는 B . 하지만 먼저 아래의 모든 해치 영역 전체를 살펴본 다음 나중에 겹치는 영역만 살펴보겠습니다. 아래와 같이 일부 부울 표현식을 위의 영역에 할당해 보겠습니다. 왼쪽 아래에는 A에 대한 빨간색 수평 해치 영역이 있습니다. . B에 대한 파란색 수직 해치 영역이 있습니다. . 양쪽의 전체 영역을 보면 해치 스타일, 모든 해치 영역의 합계에 관계없이 포괄적인 OR에 해당하는 오른쪽 위의 그림을 얻습니다. A, B의 함수입니다. 부울 표현식은 A+B입니다. . 이것은 45o로

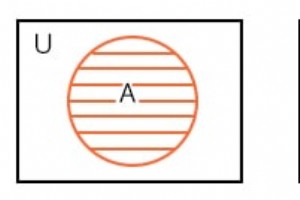
수학자들은 벤 다이어그램을 사용합니다. 집합의 논리적 관계를 표시하기 위해 (객체의 컬렉션) 서로에게. 대수학이나 다른 수학 연구에서 이미 벤 다이어그램을 본 적이 있을 것입니다. 있다면 겹치는 원과 연합을 기억할 것입니다. 및 교차로 세트 수. 벤다이어그램의 겹치는 원을 검토합니다. 디지털 전자 제품에서 사용되는 용어이므로 합집합과 교집합 대신 OR 및 AND라는 용어를 채택할 것입니다. 벤 다이어그램은 이전 장의 부울 대수학을 Karnaugh 지도로 연결합니다. Boolean algebra에 대해 이미 알고 있는 내용을 Ve